12.3: 算术序列
- Page ID
- 203864
在本节结束时,您将能够:
- 确定序列是否为算术
- 找出算术序列的通用项(\(n\)第 1 项)
- 求算术序列首\(n\)项的总和
在开始之前,请参加这个准备测验。
- 计算\(4n−1\)整数\(1, 2, 3\),然后\(4\)。
如果您错过了此问题,请查看示例 1.6。 - 求解方程组:\(\left\{\begin{array}{l}{x+y=7} \\ {3 x+4 y=23}\end{array}\right.\).
如果您错过了此问题,请查看示例 4.9。 - 如果\(f(n)=\frac{n}{2}(3 n+5)\),找到\(f(1)+f(20)\)。
如果你错过了这个问题,请查看示例 3.49。
确定序列是否为算术
最后一节介绍了序列,现在我们将研究两种特定类型的序列,每种序列都有特殊的属性。 在本节中,我们将介绍算术序列,在下一节中,我们将介绍几何序列。
算术序列是连续项之间差异恒定的序列。 算术序列中连续项 a_ {n}-a_ {n-1} 之间的差异是\(d\)\(n\)大于或等于两个的常见区别。
算术序列是连续项之间的差异始终相同的序列。
连续项 a_ {n}-a_ {n-1} 之间的差异是\(d\)\(n\)大于或等于两个的常见差异。
确定每个序列是否为算术序列。 如果是,请指出共同的区别。
- \(5,9,13,17,21,25, \dots\)
- \(4,9,12,17,20,25, \dots\)
- \(10,3,-4,-11,-18,-25, \dots\)
解决方案:
为了确定序列是否为算术,我们找到了所示连续项的差异。
一个。\(\begin{array}{cccccc}{5,} & {9,} & {13,} & {17} & {21,} & {25, \ldots} \\ {\text { Find the difference of the consecutive terms.}} & {9-5} & {13-9} & {17-13} & {21-17} & {25-21} \\ & {4} & {4} & {4} & {4}&{4}\end{array}\)
该序列是算术的。 共同的区别是\(d=4\)。
b。\(\begin{array}{cccccc}{4,} & {9,} & {12,} & {17} & {20,} & {25, \ldots} \\ {\text { Find the difference of the consecutive terms.}} & {9-4} & {12-9} & {17-12} & {20-17} & {25-20} \\ & {2} & {3} & {5} & {3}&{5}\end{array}\)
该序列不是算术的,因为连续项之间的所有差异都不相同。 没有共同的区别。
c。\(\begin{array}{cccccc}{10,} & {3,} & {-4,} & {-11} & {-18,} & {-25, \ldots} \\ {\text { Find the difference of the consecutive terms.}} & {3-10} & {-4-3} & {-11-(-4)} & {-18-(-11)} & {-25-(-18)} \\ & {-7} & {-7} & {-7} & {-7}&{-7}\end{array}\)
答案:
该序列是算术的。 共同的区别是\(d=-7\)。
确定每个序列是否为算术序列。 如果是,请指出共同的区别。
- \(9,20,31,42,53,64, \dots\)
- \(12,6,0,-6,-12,-18, \dots\)
- \(7,1,10,4,13,7, \dots\)
- 回答
-
- 该序列是算术运算,有共同的区别\(d=11\)。
- 该序列是算术运算,有共同的区别\(d=-6\)。
- 该序列不是算术的,因为连续项之间的所有差异都不相同。
确定每个序列是否为算术序列。 如果是,请指出共同的区别。
- \(-4,4,2,10,8,16, \dots\)
- \(-3,-1,1,3,5,7, \dots\)
- \(7,2,-3,-8,-13,-18, \dots\)
- 回答
-
- 该序列不是算术的,因为连续项之间的所有差异都不相同。
- 该序列是算术运算,有共同的区别\(d=2\)。
- 该序列是算术运算,有共同的区别\(d=−5\)。
如果我们知道第一个项和共同的区别\(d\),我们可以列出序列中有限数量的项。\(a_{1}\)
写下序列的前五个项,其中第一个项是\(5\),共同的区别是\(d=−6\)。
解决方案:
我们从第一个术语开始,再加上共同的区别。 然后我们在该结果中添加共同差异以得出下一个学期,依此类推。
\(\begin{array}{cccc}{a_{1}} & {a_{2}} & {a_{3}} & {a_{4}} & {a_{5}} \\ {5} & {5+(-6)} & {-1+(-6)} & {-7+(-6)} & {-13+(-6)} \\ {}&{-1} & {-7} & {-13} & {-19}\end{array}\)
答案:
顺序是\(5,-1,-7,-13,-19, \dots\)
写下序列的前五个项,其中第一个项是\(7\),共同的区别是\(d=−4\)。
- 回答
-
\(7,3,-1,-5,-9, \dots\)
写下序列的前五个项,其中第一个项是\(11\),共同的区别是\(d=−8\)。
- 回答
-
\(11,3,-5,-13,-21, \dots\)
求算术序列的通用项(\(n\)第 1 项)
就像我们找到了序列通用项的公式一样,我们也可以找到算术序列的通用项的公式。
让我们写一个序列的前几个项,其中第一个项是\(a_{1}\),共同的区别是\(d\)。 然后,我们将寻找一种图案。
当我们寻找一种模式时,我们会发现每个术语都以开头\(a_{1}\)。
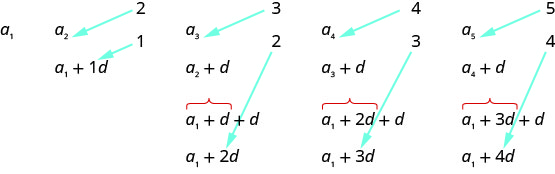
第一个术语加\(0d\)了\(a_{1}\),第二个术语加了\(1d\),第三个术语加了\(2d\),第四个术语加了\(3d\),第五个术语加\(4d\)了。 相加\(ds\)的数字比术语的数目少一。\(a_{1}\) 这使我们得出以下几点
\(a_{n}=a_{1}+(n-1) d\)
具有第一项的算术序列的通用项\(a_{1}\)和常见区别\(d\)是
\(a_{n}=a_{1}+(n-1) d\)
我们将在下一个示例中使用此公式来查找序列的第 15 项。
找出序列的第十五项,其中第一个项是\(3\),共同的区别是\(6\)。
解决方案:
\(\begin{array}{cc}{\text{To find the fifteenth term, }a_{15}\text{, use the formula with } a_{1}=3 \:\text{and} \:d=6.}&{a_{n}=a_{1}+(n-1) d} \\ {\text{Substitute in the values.}}&{a_{15}=3+(15-1) 6} \\{\text{Simplify.}}& {a_{15}=3+(14) 6} \\ {}&{a_{15}=87}\end{array}\)
找出序列的第二十七项,其中第一个项是\(7\),共同差异是\(9\)。
- 回答
-
\(241\)
找出序列的第十八项,其中第一个项是\(13\),共同差异是\(−7\)。
- 回答
-
\(-106\)
有时我们不知道第一个术语,在找到所请求的术语之前,我们必须使用其他给定的信息来找到它。
找出序列的第十二项,其中第七项是\(10\),共同差异是\(−2\)。 给出通用术语的公式。
解决方案:
要首先找到第一个项,\(a_{1}\)请使用带有\(a_{7}=10\)\(n=7\)、和的公式\(d=−2\)。 在值中替换。 简化。
\(a_{n}=a_{1}+(n-1) d\)
\(10=a_{1}+(7-1)(-2)\)
\(10=a_{1}+(6)(-2)\)
\(10=a_{1}-12\)
\(a_{1}=22\)
使用带有\(a_{12}\)\(a_{1}=22\)、和的公式找到第十二\(n=12\)个项\(d=-2\)。 在值中替换。 简化。
\(a_{n}=a_{1}+(n-1) d\)
\(a_{12}=22+(12-1)(-2)\)
\(a_{12}=22+(11)(-2)\)
\(a_{12}=0\)
序列的第十二项是\(0, a_{12}=0\)
要找到通用术语,请将这些值替换到公式中。
\(a_{n}=a_{1}+(n-1) d\)
\(a_{n}=22+(n-1)(-2)\)
\(a_{n}=22-2 n+2\)
答:
通用术语是\(a_{n}=-2 n+24\)
找出序列的第十一个项,其中第九项是\(8\),共同的区别是\(−3\)。 给出通用术语的公式。
- 回答
-
\(a_{11}=2 .\)一般术语是\(a_{n}=-3 n+35\)
找出序列的第十九项,其中第五项是\(1\),共同差异为\(−4\)。给出通用项的公式。
- 回答
-
\(a_{19}=-55 .\)一般术语是\(a_{n}=-4 n+21\)
有时,给出的信息会使我们得出两个未知数中的两个方程。 然后,我们使用求解方程组的方法来找到所需的值。
找出序列的第一个项和共同差异,其中第五项是\(19\),第十一个项是\(37\)。 给出通用术语的公式。
解决方案:
既然我们知道两个项,我们可以使用通用项的公式来创建方程组。
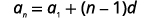 |
|
| 我们知道\(a_{5}\)和的值\(a_{11}\),因此我们将使用\(n=5\)和\(n=11\)。 | 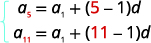 |
在值中替换,\(a_{5}=19\)和\(a_{11}=37\)。 |
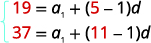 |
| 简化。 | 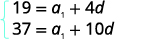 |
| 准备通过将顶部方程乘以来消除该项\(−1\)。\(a_{1}\) 添加方程。 |
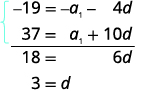 |
| 用第一个方程替换\(d=3\)回去。 | 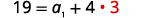 |
| 求解\(a_{1}\)。 |  |
| 使用带有 and 的\(a_{1}=7\)公式\(d=3\)。 | 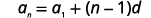 |
| 在值中替换。 | 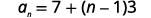 |
| 简化。 | 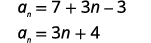 |
| 第一个学期是\(a_{1}=7\)。 共同的区别是\(d=3\)。 |
|
| 该序列的通用术语是\(a_{n}=3n+4\)。 |
答案:
该序列的通用术语是\(a_{n}=3n+4\)。
找出序列的第一个项和常见差异,其中第四项是\(17\),第十三项是\(53\)。 给出通用术语的公式。
- 回答
-
\(a_{1}=5, d=4 .\)一般术语是\(a_{n}=4 n+1\)。
找出第三项和第十二项为的序列的第一个项\(2\)和共同差异\(−25\)。 给出通用术语的公式。
- 回答
-
\(a_{1}=8, d=-3 .\)一般术语是\(a_{n}=-3 n+11\)。
求算术序列首\(n\)项之和
与一般序列一样,求出算术序列的总和通常很有用。 任何算术序列的第一\(n\)项的总和写为\(S_{n} =a_{1} +a_{2} +a_{3} +\ldots +a_{n}\)。\(S_{n}\) 仅通过将所有术语相加就能找到总和可能很乏味。 因此,我们还可以开发一个公式,使用序列的第一个和最后一个项来求出序列的总和。
我们可以开发出这个新公式,方法是先用第一个项写出总和\(a_{1}\),然后继续加上 a\(d\) 得出下一个项为:
\(S_{n}=a_{1}+\left(a_{1}+d\right)+\left(a_{1}+2 d\right)+\ldots+a_{n}\)。
我们也可以反转项的顺序,用以开头写出总和,\(a_{n}\)然后\(d\)继续减去,得出下一个项为
\(S_{n}=a_{n}+\left(a_{n}-d\right)+\left(a_{n}-2 d\right)+\ldots+a_{1}\)。
如果我们将这两个表达式相加得出算术序列中前\(n\)项的总和,则可以得出任何算术序列的第一\(n\)项之和的公式。
\(\begin{aligned} &S_{n}= a_{1} \quad+\left(a_{1}+d\right)+\left(a_{1}+2 d\right)+\ldots+a_{n} \\+&S_{n} =a_{n} \quad+\left(a_{n}-d\right)+\left(a_{n}-2 d\right)+\ldots+a_{1} \\ \hline \\ &2S_{n}=(a_{1}+a_{n})+(a_{1}+a_{n})+(a_{1}+a_{n})+\dots+(a_{1}+a_{n}) \end{aligned}\)
因为方程右侧有\(n\)总和,所以我们将右边的总和重写为\(n(a_{1}+a_{n})\)。\((a_{1}+a_{n})\)
\(2 S_{n}=n\left(a_{1}+a_{n}\right)\)
我们除以二来求解\(S_{n}\)。
\(S_{n}=\frac{n}{2}\left(a_{1}+a_{n}\right)\)
这为我们提供了一个算术序列首\(n\)项之和的通用公式。
算术序列的第一\(n\)项之和为\(S_{n}\)
\(S_{n}=\frac{n}{2}\left(a_{1}+a_{n}\right)\)
其中\(a_{1}\)是第一项,\(a_{n}\)是\(n\)第 3 项。
我们在下一个示例中应用这个公式,其中给出了序列的前几个项。
求算术序列首\(30\)项的总和:\(8, 13, 18, 23, 28, …\)
解决方案:
为了找到总和,我们将使用公式\(S_{n}=\frac{n}{2}\left(a_{1}+a_{n}\right)\)。 我们知道\(a_{1}=8, d=5\)和\(n=30\),但是我们需要找到\(a_{n}\)才能使用总和公式。
找出\(a_{n}\)位置\(a_{1}=8, d=5\)和\(n=30\). 简化。
\(\begin{aligned} a_{n} &=a_{1}+(n-1) d \\ a_{30} &=8+(30-1) 5 \\ a_{30} &=8+(29) 5 \\ a_{30} &=153 \end{aligned}\)
知道\(a_{1}=8, n=30\)\(a_{30}=153\),然后使用总和公式。 在值中替换。 简化。 简化。
\(\begin{aligned} S_{n} &=\frac{n}{2}\left(a_{1}+a_{n}\right) \\ S_{30} &=\frac{30}{2}(8+153) \\ S_{30} &=15(161) \\ S_{30} &=2,415 \end{aligned}\)
求算术序列首\(30\)项的总和:\(5, 9, 13, 17, 21, …\)
- 回答
-
\(1,890\)
求算术序列首\(30\)项的总和:\(7, 10, 13, 16, 19, …\)
- 回答
-
\(1,515\)
在下一个示例中,我们得到序列的通用项,并要求我们找出第一个\(50\)项的总和。
求通用项为的算术序列中前\(50\)项的总和\(a_{n}=3n−4\)。
解决方案:
为了找到总和,我们将使用公式\(S_{n}=\frac{n}{2}\left(a_{1}+a_{n}\right)\)。 我们知道\(n=50\),但是我们需要找到\(a_{1}\)和\(a_{n}\)才能使用总和公式。
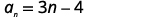 |
|
| 通过替换查找\(a_{1}\)\(n=1\)。 | 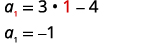 |
| \(a_{n}\)通过替换查找\(n=50\)。 | 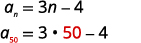 |
| 简化。 | 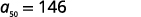 |
| 了解\(n=50, a_{1}=−1,\)并\(a_{50}=146\)使用总和公式。 | 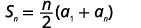 |
| 在值中替换。 | 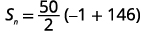 |
| 简化。 | 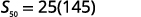 |
| 简化。 | 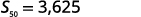 |
求通用项为的算术序列中前\(50\)项的总和\(a_{n}=2n−5\)。
- 回答
-
\(2,300\)
求通用项为的算术序列中前\(50\)项的总和\(a_{n}=4n+3\)。
- 回答
-
\(5,250\)
在下一个示例中,我们以求和表示法给出了总和。 添加所有术语会很乏味,因此我们提取所需的信息,以使用公式求出第一个\(n\)项的总和。
找到总和:\(\sum_{i=1}^{25}(4 i+7)\).
解决方案:
为了找到总和,我们将使用公式\(S_{n}=\frac{n}{2}\left(a_{1}+a_{n}\right)\)。 我们知道\(n=25\),但是我们需要找到\(a_{1}\)和\(a_{n}\)才能使用总和公式。
| 扩展求和表示法。 |
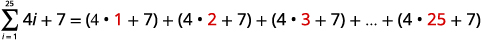
|
| 简化。 |
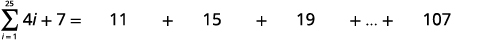
|
| 识别\(a_{1}\)。 |  |
| 识别\(a_{25}\)。 |

|
| 知道\(n=25, a_{1}=11\)并\(a_{25} = 107\)使用总和公式。 |  |
| 在值中替换。 |  |
| 简化。 |  |
| 简化。 |  |
找到总和:\(\sum_{i=1}^{30}(6 i-4)\).
- 回答
-
\(2,670\)
找到总和:\(\sum_{i=1}^{35}(5 i-3)\).
- 回答
-
\(3,045\)
访问这些在线资源以获取更多指导和使用算术序列进行练习
关键概念
- 算术序列
的通用项(\(n\)第 1 项)具有第一项\(a_{1}\)和共同差异的算术序列的总\(d\)项是\(a_{n}=a_{1}+(n-1) d\)
- 算@@ \(n\)术序列第一项的总和算术序列
的前\\(n\) 项的总和,其中\(a_{1}\)是第一项,\(a_{n}\)是\(n\)第 th 项\(S_{n}\)\(S_{n}=\frac{n}{2}\left(a_{1}+a_{n}\right)\)
词汇表
- 算术序列
- 算术序列是连续项之间差异恒定的序列。
- 共同的区别
- 对于\(n\)大于或等于两个\(a_{n}−a_{n−1}\),算术序列中连续项之间的差异是\(d\)常见的区别。


