第 11 章复习练习
- Page ID
- 204378
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)
章节复习练习
距离和中点公式；圆圈
在以下练习中，找出两点之间的距离。 如果需要，四舍五入到最接近的十分之一。
- \((-5,1)\)和\((-1,4)\)
- \((-2,5)\)和\((1,5)\)
- \((8,2)\)和\((-7,-3)\)
- \((1,-4)\)和\((5,-5)\)
- 回答
-
2。 \(d=3\)
4。 \(d=\sqrt{17}, d \approx 4.1\)
在以下练习中，找出给定端点的线段的中点。
- \((-2,-6)\)和\((-4,-2)\)
- \((3,7)\)和\((5,1)\)
- \((-8,-10)\)和\((9,5)\)
- \((-3,2)\)和\((6,-9)\)
- 回答
-
2。 \((4,4)\)
4。 \(\left(\frac{3}{2},-\frac{7}{2}\right)\)
在以下练习中，使用给定信息写出圆方程的标准形式。
- 半径为\(15\)，中心为\((0,0)\)
- 半径为\(\sqrt{7}\)，中心为\((0,0)\)
- 半径为\(9\)，中心为\((-3,5)\)
- 半径为\(7\)，中心为\((-2,-5)\)
- 中心是\((3,6)\)，圆上的一个点是\((3,-2)\)
- 中心是\((2,2)\)，圆上的一个点是\((4,4)\)
- 回答
-
2。 \(x^{2}+y^{2}=7\)
4。 \((x+2)^{2}+(y+5)^{2}=49\)
6。 \((x-2)^{2}+(y-2)^{2}=8\)
在以下练习中，
- 找到中心和半径，然后
- 绘制每个圆圈的图形。
- \(2 x^{2}+2 y^{2}=450\)
- \(3 x^{2}+3 y^{2}=432\)
- \((x+3)^{2}+(y-5)^{2}=81\)
- \((x+2)^{2}+(y+5)^{2}=49\)
- \(x^{2}+y^{2}-6 x-12 y-19=0\)
- \(x^{2}+y^{2}-4 y-60=0\)
- 回答
-
2。
- 半径：\(12,\)中心：\((0,0)\)
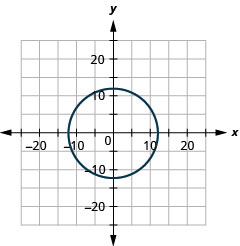
图 11.E.1 4。
- 半径：\(7,\)中心：\((-2,-5)\)
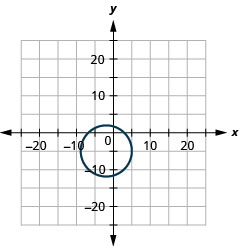
图 11.E.2 6。
- 半径：\(8,\)中心：\((0,2)\)
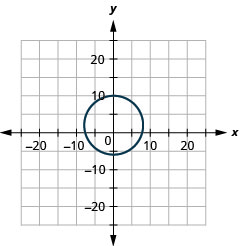
图 11.E.3
抛物线
在以下练习中，使用每个方程的属性绘制其图表。
- \(y=x^{2}+4 x-3\)
- \(y=2 x^{2}+10 x+7\)
- \(y=-6 x^{2}+12 x-1\)
- \(y=-x^{2}+10 x\)
- 回答
-
2。
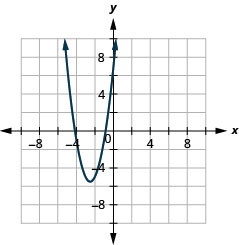
图 11.E.4 4。
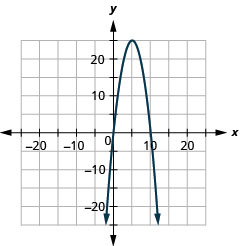
图 11.E.5
在以下练习中，
- 用标准形式写下方程式，然后
- 使用标准形式的属性绘制方程图。
- \(y=x^{2}+4 x+7\)
- \(y=2 x^{2}-4 x-2\)
- \(y=-3 x^{2}-18 x-29\)
- \(y=-x^{2}+12 x-35\)
- 回答
-
2。
- \(y=2(x-1)^{2}-4\)
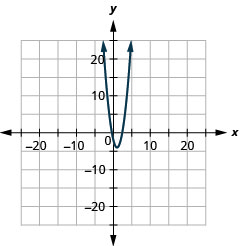
图 11.E.6 4。
- \(y=-(x-6)^{2}+1\)
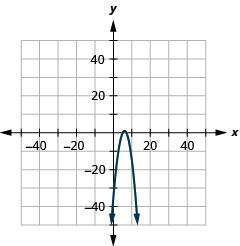
图 11.E.7
在以下练习中，使用每个方程的属性绘制其图表。
- \(x=2 y^{2}\)
- \(x=2 y^{2}+4 y+6\)
- \(x=-y^{2}+2 y-4\)
- \(x=-3 y^{2}\)
- 回答
-
2。
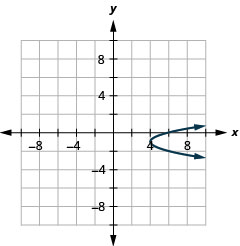
图 11.E.8 4。
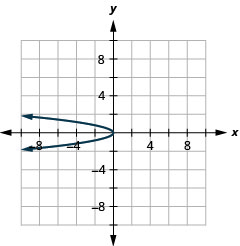
图 11.E.9
在以下练习中，
- 用标准形式写下方程式，然后
- 使用标准形式的属性绘制方程图。
- \(x=4 y^{2}+8 y\)
- \(x=y^{2}+4 y+5\)
- \(x=-y^{2}-6 y-7\)
- \(x=-2 y^{2}+4 y\)
- 回答
-
2。
- \(x=(y+2)^{2}+1\)
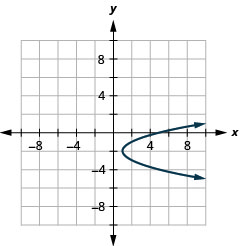
图 11.E.10 4。
- \(x=-2(y-1)^{2}+2\)
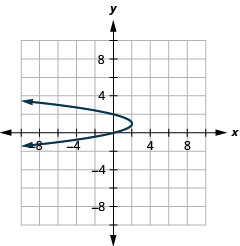
图 11.E.11
在以下练习中，创建在所示桥梁基础上形成的抛物线拱的方程。 以标准形式给出答案。
1。
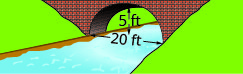
2。
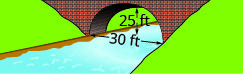
- 回答
-
2。 \(y=-\frac{1}{9} x^{2}+\frac{10}{3} x\)
省略号
在以下练习中，绘制每个椭圆的图形。
- \(\frac{x^{2}}{36}+\frac{y^{2}}{25}=1\)
- \(\frac{x^{2}}{4}+\frac{y^{2}}{81}=1\)
- \(49 x^{2}+64 y^{2}=3136\)
- \(9 x^{2}+y^{2}=9\)
- 回答
-
2。
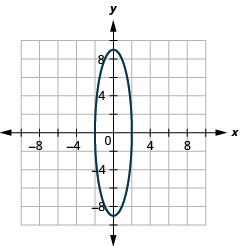
图 11.E.14 4。
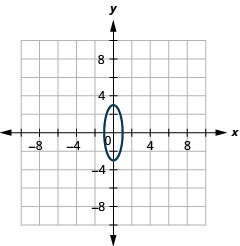
图 11.E.15
在以下练习中，找到图中显示的椭圆的方程。
1。
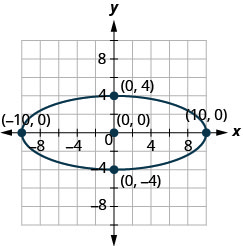
2。
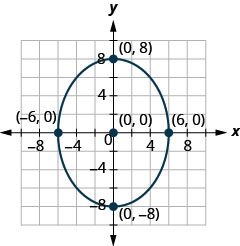
- 回答
-
2。 \(\frac{x^{2}}{36}+\frac{y^{2}}{64}=1\)
在以下练习中，绘制每个椭圆的图形。
- \(\frac{(x-1)^{2}}{25}+\frac{(y-6)^{2}}{4}=1\)
- \(\frac{(x+4)^{2}}{16}+\frac{(y+1)^{2}}{9}=1\)
- \(\frac{(x-5)^{2}}{16}+\frac{(y+3)^{2}}{36}=1\)
- \(\frac{(x+3)^{2}}{9}+\frac{(y-2)^{2}}{25}=1\)
- 回答
-
2。
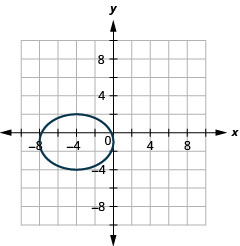
图 11.E.18 4。
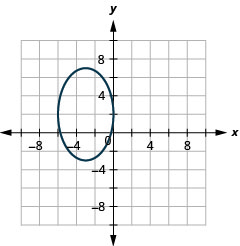
图 11.E.19
在以下练习中，
- 用标准形式写下方程式然后
- 图表。
- \(x^{2}+y^{2}+12 x+40 y+120=0\)
- \(25 x^{2}+4 y^{2}-150 x-56 y+321=0\)
- \(25 x^{2}+4 y^{2}+150 x+125=0\)
- \(4 x^{2}+9 y^{2}-126 x+405=0\)
- 回答
-
2。
- \(\frac{(x-3)^{2}}{4}+\frac{(y-7)^{2}}{25}=1\)
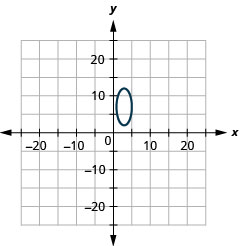
图 11.E.20 4。
- \(\frac{x^{2}}{9}+\frac{(y-7)^{2}}{4}=1\)
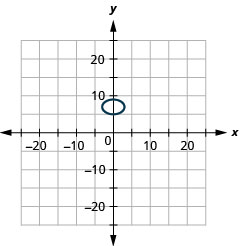
图 11.E.21
在以下练习中，写下所描述的椭圆的方程。
- 彗星围绕太阳在椭圆轨道上移动。 彗星离太阳最近的距离大约是\(10\)非盟，最远的距离大约是\(90\)非盟。 太阳是椭圆轨道的焦点之一。 让椭圆以原点为中心并在 AU 中标记轴，轨道将如下图所示。 使用图表为彗星的椭圆轨道写出方程。
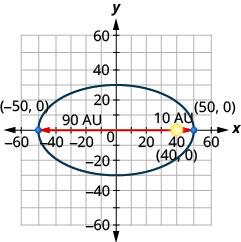
- 回答
-
1。 解决
双曲线
在以下练习中，绘制图表。
- \(\frac{x^{2}}{25}-\frac{y^{2}}{9}=1\)
- \(\frac{y^{2}}{49}-\frac{x^{2}}{16}=1\)
- \(9 y^{2}-16 x^{2}=144\)
- \(16 x^{2}-4 y^{2}=64\)
- 回答
-
1。
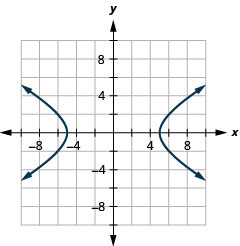
图 11.E.23 3。
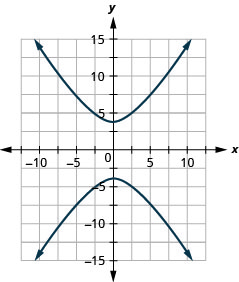
图 11.E.24
在以下练习中，绘制图表。
- \(\frac{(x+1)^{2}}{4}-\frac{(y+1)^{2}}{9}=1\)
- \(\frac{(x-2)^{2}}{4}-\frac{(y-3)^{2}}{16}=1\)
- \(\frac{(y+2)^{2}}{9}-\frac{(x+1)^{2}}{9}=1\)
- \(\frac{(y-1)^{2}}{25}-\frac{(x-2)^{2}}{9}=1\)
- 回答
-
1。
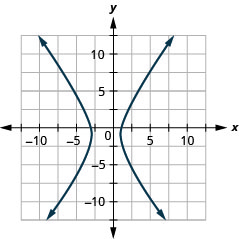
图 11.E.25 3。
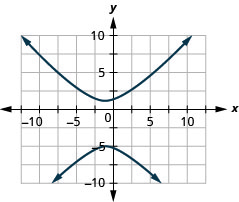
图 11.E.26
在以下练习中，
- 用标准形式写下方程式然后
- 图表。
- \(4 x^{2}-16 y^{2}+8 x+96 y-204=0\)
- \(16 x^{2}-4 y^{2}-64 x-24 y-36=0\)
- \(4 y^{2}-16 x^{2}+32 x-8 y-76=0\)
- \(36 y^{2}-16 x^{2}-96 x+216 y-396=0\)
- 回答
-
1。
- \(\frac{(x+1)^{2}}{16}-\frac{(y-3)^{2}}{4}=1\)
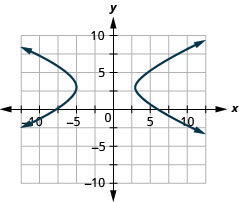
图 11.E.27 3。
- \(\frac{(y-1)^{2}}{16}-\frac{(x-1)^{2}}{4}=1\)
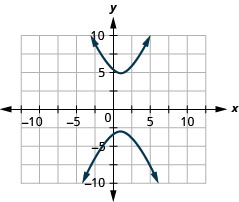
图 11.E.28
在以下练习中，确定图表的类型。
-
- \(16 y^{2}-9 x^{2}-36 x-96 y-36=0\)
- \(x^{2}+y^{2}-4 x+10 y-7=0\)
- \(y=x^{2}-2 x+3\)
- \(25 x^{2}+9 y^{2}=225\)
-
- \(x^{2}+y^{2}+4 x-10 y+25=0\)
- \(y^{2}-x^{2}-4 y+2 x-6=0\)
- \(x=-y^{2}-2 y+3\)
- \(16 x^{2}+9 y^{2}=144\)
- 回答
-
1。
- 双曲线
- 圈子
- 抛物线
- 椭圆
求解非线性方程组
在以下练习中，使用图形求解方程组。
- \(\left\{\begin{array}{l}{3 x^{2}-y=0} \\ {y=2 x-1}\end{array}\right.\)
- \(\left\{\begin{array}{l}{y=x^{2}-4} \\ {y=x-4}\end{array}\right.\)
- \(\left\{\begin{array}{l}{x^{2}+y^{2}=169} \\ {x=12}\end{array}\right.\)
- \(\left\{\begin{array}{l}{x^{2}+y^{2}=25} \\ {y=-5}\end{array}\right.\)
- 回答
-
1。
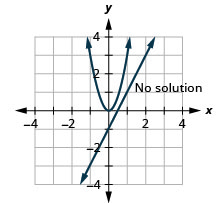
图 11.E.29 3。
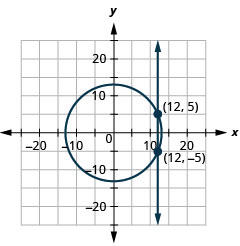
图 11.E.30
在以下练习中，使用替换求解方程组。
- \(\left\{\begin{array}{l}{y=x^{2}+3} \\ {y=-2 x+2}\end{array}\right.\)
- \(\left\{\begin{array}{l}{x^{2}+y^{2}=4} \\ {x-y=4}\end{array}\right.\)
- \(\left\{\begin{array}{l}{9 x^{2}+4 y^{2}=36} \\ {y-x=5}\end{array}\right.\)
- \(\left\{\begin{array}{l}{x^{2}+4 y^{2}=4} \\ {2 x-y=1}\end{array}\right.\)
- 回答
-
1。 \((-1,4)\)
3。 没有解决办法
在以下练习中，使用消除法求解方程组。
- \(\left\{\begin{array}{l}{x^{2}+y^{2}=16} \\ {x^{2}-2 y-1=0}\end{array}\right.\)
- \(\left\{\begin{array}{l}{x^{2}-y^{2}=5} \\ {-2 x^{2}-3 y^{2}=-30}\end{array}\right.\)
- \(\left\{\begin{array}{l}{4 x^{2}+9 y^{2}=36} \\ {3 y^{2}-4 x=12}\end{array}\right.\)
- \(\left\{\begin{array}{l}{x^{2}+y^{2}=14} \\ {x^{2}-y^{2}=16}\end{array}\right.\)
- 回答
-
1。 \((-\sqrt{7}, 3),(\sqrt{7}, 3)\)
3。 \((-3,0),(0,-2),(0,2)\)
在以下练习中，使用方程组解决问题。
- 两个数字的平方和为\(25\)。 数字的区别是\(1\)。 找到数字。
- 两个数字的平方之差为\(45\)。 第一个数字的平方与第二个数字的平方的两倍之差为\(9\)。 找到数字。
- 矩形的周长为\(58\)米，其面积为\(210\)平方米。 找到矩形的长度和宽度。
- 科尔顿为他的厨房购买了一台更大的微波炉。 微波炉正面的对角线长\(34\)度为英寸。 正面的面积也为\(480\)平方英寸。 微波炉的长度和宽度是多少？
- 回答
-
1。 \(-3\)and\(-4\) 或 an\(4\) d\(3\)
3。 如果长度为\(14\)英寸，则宽度为\(15\)英寸。 如果长度为\(15\)英寸，则宽度为\(14\)英寸。
练习测试
在以下练习中，找出各点与具有给定端点的线段中点之间的距离。 根据需要四舍五入到最接近的十分之一。
- \((-4,-3)\)和\((-10,-11)\)
- \((6,8)\)和\((-5,-3)\)
- 回答
-
1. 距离：\(10,\)中点：\((-7,-7)\)
在以下练习中，使用给定信息写出圆方程的标准形式。
- 半径为\(11\)，中心为\((0,0)\)
- 半径为\(12\)，中心为\((10,-2)\)
- 中心是\((-2,3)\)，圆上的一个点是\((2,-3)\)
- 找到图中显示的椭圆的方程。
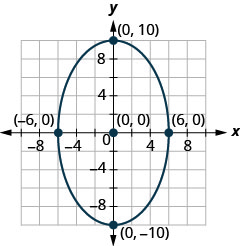
- 回答
-
1。 \(x^{2}+y^{2}=121\)
3。 \((x+2)^{2}+(y-3)^{2}=52\)
在以下练习中，
- 将每个方程的图形类型识别为圆形、抛物线、椭圆或双曲线，以及
- 绘制方程图。
- \(4 x^{2}+49 y^{2}=196\)
- \(y=3(x-2)^{2}-2\)
- \(3 x^{2}+3 y^{2}=27\)
- \(\frac{y^{2}}{100}-\frac{x^{2}}{36}=1\)
- \(\frac{x^{2}}{16}+\frac{y^{2}}{81}=1\)
- \(x=2 y^{2}+10 y+7\)
- \(64 x^{2}-9 y^{2}=576\)
- 回答
-
1。
- 椭圆
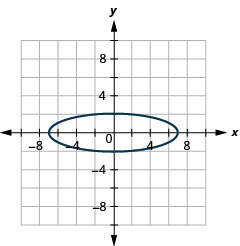
图 11.E.32 3。
- 圈子
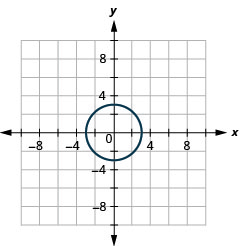
图 11.E.33 5。
- 椭圆
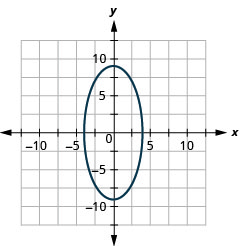
图 11.E.34 7。
- 双曲线
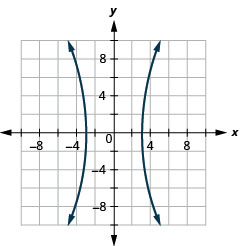
图 11.E.35
在以下练习中，
- 将每个方程的图形类型识别为圆形、抛物线、椭圆或双曲线，
- 用标准形式写出方程式，然后
- 绘制方程图。
- \(25 x^{2}+64 y^{2}+200 x-256 y-944=0\)
- \(x^{2}+y^{2}+10 x+6 y+30=0\)
- \(x=-y^{2}+2 y-4\)
- \(9 x^{2}-25 y^{2}-36 x-50 y-214=0\)
- \(y=x^{2}+6 x+8\)
- 通过图形求解非线性方程组:\(\left\{\begin{array}{l}{3 y^{2}-x=0} \\ {y=-2 x-1}\end{array}\right.\).
- 使用替换求解非线性方程组:\(\left\{\begin{array}{l}{x^{2}+y^{2}=8} \\ {y=-x-4}\end{array}\right.\).
- 使用消除法求解非线性方程组：\(\left\{\begin{array}{l}{x^{2}+9 y^{2}=9} \\ {2 x^{2}-9 y^{2}=18}\end{array}\right.\)
- 创建在所示桥梁基础上形成的抛物线拱的方程。 以\(y=a x^{2}+b x+c\)表格给出答案。
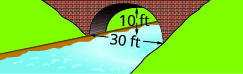
10。 一颗彗星围绕太阳在椭圆轨道上移动。 彗星离太阳最近的距离大约是\(20\)非盟，最远的距离大约是\(70\)非盟。 太阳是椭圆轨道的焦点之一。 让椭圆以原点为中心并在 AU 中标记轴，轨道将如下图所示。 使用图表为彗星的椭圆轨道写出方程。
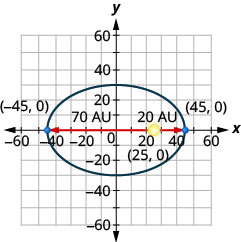
11。 两个数字之\(22\)和为，乘积为\(−240\)。 找到数字。
12。 奥利弗的祖父母在生日那天给她买了一台新的宽屏电视。 在打开之前，她想确保它适合她的娱乐中心。 电视是\(55\)”。 电视机的大小是根据屏幕的对角线测量的，宽屏的长度大于宽度。 屏幕的面积也为\(1452\)平方英寸。 她的娱乐中心有一个电视插件，长度为\(50\)英寸，宽度\(40\)为英寸。 电视屏幕的长度和宽度是多少？它适合 Olive 的娱乐中心吗？
- 回答
-
2。
- 圈子
- \((x+5)^{2}+(y+3)^{2}=4\)
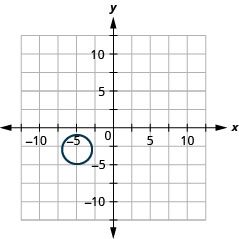
图 11.E.38 4。
- 双曲线
- \(\frac{(x-2)^{2}}{25}-\frac{(y+1)^{2}}{9}=1\)
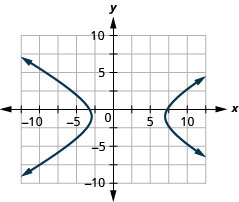
图 11.E.39 6。 没有解决办法
8。 \((0,-3),(0,3)\)
10。 \(\frac{x^{2}}{2025}+\frac{y^{2}}{1400}=1\)
12。 长度为\(44\)英寸，宽度为\(33\)英寸。 电视将适合 Olive 的娱乐中心。
词汇表
- 非线性方程组
- 非线性方程组是指至少有一个方程不是线性的系统。