11.6E：练习

Last updated
Save as PDF

Page ID: 204377

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

练习成就完美

练习\(\PageIndex{17}\) Solve a System of Nonlinear Equations Using Graphing

在以下练习中，使用图形求解方程组。

\(\left\{\begin{array}{l}{y=2 x+2} \\ {y=-x^{2}+2}\end{array}\right.\)
\(\left\{\begin{array}{l}{y=6 x-4} \\ {y=2 x^{2}}\end{array}\right.\)
\(\left\{\begin{array}{l}{x+y=2} \\ {x=y^{2}}\end{array}\right.\)
\(\left\{\begin{array}{l}{x-y=-2} \\ {x=y^{2}}\end{array}\right.\)
\(\left\{\begin{array}{l}{y=\frac{3}{2} x+3} \\ {y=-x^{2}+2}\end{array}\right.\)
\(\left\{\begin{array}{l}{y=x-1} \\ {y=x^{2}+1}\end{array}\right.\)
\(\left\{\begin{array}{l}{x=-2} \\ {x^{2}+y^{2}=4}\end{array}\right.\)
\(\left\{\begin{array}{l}{y=-4} \\ {x^{2}+y^{2}=16}\end{array}\right.\)
\(\left\{\begin{array}{l}{x=2} \\ {(x+2)^{2}+(y+3)^{2}=16}\end{array}\right.\)
\(\left\{\begin{array}{l}{y=-1} \\ {(x-2)^{2}+(y-4)^{2}=25}\end{array}\right.\)
\(\left\{\begin{array}{l}{y=-2 x+4} \\ {y=\sqrt{x}+1}\end{array}\right.\)
\(\left\{\begin{array}{l}{y=-\frac{1}{2} x+2} \\ {y=\sqrt{x}-2}\end{array}\right.\)

回答

2。

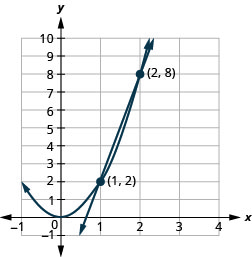
此图显示了一个系统的方程，在 x y 坐标平面上，y 等于 6 x 减去 4（一条直线），y 等于 2 x 平方，即抛物线。抛物线的顶点是 (0, 0)，抛物线向上打开。该线的斜率为 6。直线和抛物线在标注的点 (1、2) 和 (2、8) 处相交。解决方案是 (1、2) 和 (2、8)。 — 图 11.5.61

4。

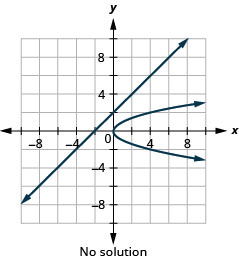
此图显示了方程组的方程，x 减去 y 等于负 2（表示直线），x 等于 y 坐标平面上的 y 平方，即向右开口的抛物线。抛物线的顶点是 (0, 0)，它穿过点 (1, 1) 和 (1，负 1)。直线的斜率为 1，Y 截距为 2。直线和抛物线不相交，因此系统没有解决方案。 — 图 11.5.62

6。

这张图显示了一个系统的方程，y 是 x 减 1，这是一条直线，y 等于 x 平方加 1，在 x y 坐标平面上，这是一个向上开启的抛物线。抛物线的顶点是 (0, 1)，它穿过点（负 1, 2）和（1, 2）。直线的斜率为 1，Y 截距为负 1。直线和抛物线不相交，因此系统没有解决方案。 — 图 11.5.63

8。

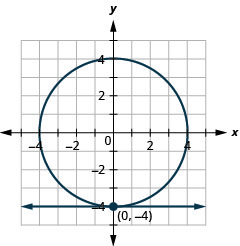
此图显示了一个系统的方程，在 x y 坐标平面上，x 等于负 2（表示直线），x 平方加 y 平方等于 16（即圆）。这条线是水平的。圆的中心为 (0, 0)，圆的半径为 4。直线和圆在（负 2, 0）处相交，因此系统的解是（负 2, 0）。 — 图 11.5.64

10。

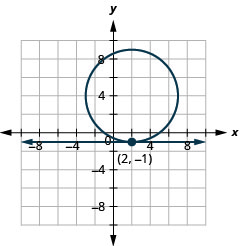
此图显示了方程组的方程，x 等于 2，即一条直线，数量 x 减去 2 末端数量的平方加上数量 y 减去 4 终止数量的平方等于 25（即圆），在 x y 坐标平面上。这条线是水平的。圆的中心为 (2, 4)，圆的半径为 5。直线和圆在 (2，负 1) 处相交，因此系统的解为 (2，负 1)。 — 图 11.5.65

12。

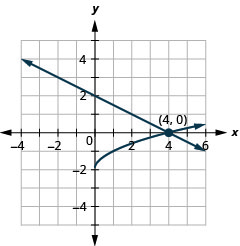
此图显示了一个系统的方程，在 x y 坐标平面上，y 等于负一半 x 加 2（一条直线），y 等于 x 减去 2 的平方根。 y 的曲线等于 x 减去 2 的平方根。y 的曲线等于 x 加 1 的平方根，其中 x 大于或等于 0，y 大于或等于负 2。直线和平方根曲线在 (4, 0) 处相交，因此解是 (4, 0)。 — 图 11.5.66

练习\(\PageIndex{18}\) Solve a System of Nonlinear Equations Using Substitution

在以下练习中，使用替换求解方程组。

\(\left\{\begin{array}{l}{x^{2}+4 y^{2}=4} \\ {y=\frac{1}{2} x-1}\end{array}\right.\)
\(\left\{\begin{array}{l}{9 x^{2}+y^{2}=9} \\ {y=3 x+3}\end{array}\right.\)
\(\left\{\begin{array}{l}{9 x^{2}+y^{2}=9} \\ {y=x+3}\end{array}\right.\)
\(\left\{\begin{array}{l}{9 x^{2}+4 y^{2}=36} \\ {x=2}\end{array}\right.\)
\(\left\{\begin{array}{l}{4 x^{2}+y^{2}=4} \\ {y=4}\end{array}\right.\)
\(\left\{\begin{array}{l}{x^{2}+y^{2}=169} \\ {x=12}\end{array}\right.\)
\(\left\{\begin{array}{l}{3 x^{2}-y=0} \\ {y=2 x-1}\end{array}\right.\)
\(\left\{\begin{array}{l}{2 y^{2}-x=0} \\ {y=x+1}\end{array}\right.\)
\(\left\{\begin{array}{l}{y=x^{2}+3} \\ {y=x+3}\end{array}\right.\)
\(\left\{\begin{array}{l}{y=x^{2}-4} \\ {y=x-4}\end{array}\right.\)
\(\left\{\begin{array}{l}{x^{2}+y^{2}=25} \\ {x-y=1}\end{array}\right.\)
\(\left\{\begin{array}{l}{x^{2}+y^{2}=25} \\ {2 x+y=10}\end{array}\right.\)

回答

2。 \((-1,0),(0,3)\)

4。 \((2,0)\)

6。 \((12,-5),(12,5)\)

8。没有解决办法

10。 \((0,-4),(1,-3)\)

12。 \((3,4),(5,0)\)

练习\(\PageIndex{19}\) Solve a System of Nonlinear Equations Using Elimination

在以下练习中，使用消除法求解方程组。

\(\left\{\begin{array}{l}{x^{2}+y^{2}=16} \\ {x^{2}-2 y=8}\end{array}\right.\)
\(\left\{\begin{array}{l}{x^{2}+y^{2}=16} \\ {x^{2}-y=4}\end{array}\right.\)
\(\left\{\begin{array}{l}{x^{2}+y^{2}=4} \\ {x^{2}+2 y=1}\end{array}\right.\)
\(\left\{\begin{array}{l}{x^{2}+y^{2}=4} \\ {x^{2}-y=2}\end{array}\right.\)
\(\left\{\begin{array}{l}{x^{2}+y^{2}=9} \\ {x^{2}-y=3}\end{array}\right.\)
\(\left\{\begin{array}{l}{x^{2}+y^{2}=4} \\ {y^{2}-x=2}\end{array}\right.\)
\(\left\{\begin{array}{l}{x^{2}+y^{2}=25} \\ {2 x^{2}-3 y^{2}=5}\end{array}\right.\)
\(\left\{\begin{array}{l}{x^{2}+y^{2}=20} \\ {x^{2}-y^{2}=-12}\end{array}\right.\)
\(\left\{\begin{array}{l}{x^{2}+y^{2}=13} \\ {x^{2}-y^{2}=5}\end{array}\right.\)
\(\left\{\begin{array}{l}{x^{2}+y^{2}=16} \\ {x^{2}-y^{2}=16}\end{array}\right.\)
\(\left\{\begin{array}{l}{4 x^{2}+9 y^{2}=36} \\ {2 x^{2}-9 y^{2}=18}\end{array}\right.\)
\(\left\{\begin{array}{l}{x^{2}-y^{2}=3} \\ {2 x^{2}+y^{2}=6}\end{array}\right.\)
\(\left\{\begin{array}{l}{4 x^{2}-y^{2}=4} \\ {4 x^{2}+y^{2}=4}\end{array}\right.\)
\(\left\{\begin{array}{l}{x^{2}-y^{2}=-5} \\ {3 x^{2}+2 y^{2}=30}\end{array}\right.\)
\(\left\{\begin{array}{l}{x^{2}-y^{2}=1} \\ {x^{2}-2 y=4}\end{array}\right.\)
\(\left\{\begin{array}{l}{2 x^{2}+y^{2}=11} \\ {x^{2}+3 y^{2}=28}\end{array}\right.\)

回答

2。 \((0,-4),(-\sqrt{7}, 3),(\sqrt{7}, 3)\)

4。 \((0,-2),(-\sqrt{3}, 1),(\sqrt{3}, 1)\)

6。 \((-2,0),(1,-\sqrt{3}),(1, \sqrt{3})\)

8。 \((-2,-4),(-2,4),(2,-4),(2,4)\)

10。 \((-4,0),(4,0)\)

12。 \((-\sqrt{3}, 0),(\sqrt{3}, 0)\)

14。 \((-2,-3),(-2,3),(2,-3),(2,3)\)

16。 \((-1,-3),(-1,3),(1,-3),(1,3)\)

练习\(\PageIndex{20}\) Use a System of Nonlinear Equations to Solve Applications

在以下练习中，使用方程组解决问题。

两个数字之\(−6\)和为，乘积为\(8\)。找到数字。
两个数字之\(11\)和为，乘积为\(−42\)。找到数字。
两个数字的平方和为\(65\)。数字的区别是\(3\)。找到数字。
两个数字的平方和为\(113\)。数字的区别是\(1\)。找到数字。
两个数字的平方之差为\(15\)。第一个数字的平方和第二个数字的平方的两倍之差为\(30\)。找到数字。
两个数字的平方之差为\(20\)。第一个数字的平方与第二个数字的平方的两倍之差为\(4\)。找到数字。
矩形的周长为\(32\)英寸，其面积为\(63\)平方英寸。找出矩形的长度和宽度。
矩形的周长为\(52\) cm，其面积为\(165\)\(\mathrm{cm}^{2}\)。找出矩形的长度和宽度。
狄翁买了一台新的微波炉。门的对角线长\(17\)度为英寸。门的面积也为\(120\)平方英寸。微波门的长度和宽度是多少？
朱尔斯为他的厨房买了一台微波炉。微波炉正面的对角线长\(26\)度为英寸。正面的面积也为\(240\)平方英寸。微波炉的长度和宽度是多少？
罗曼找到了一台在售的宽屏电视，但不确定它是否适合他的娱乐中心。电视是\(60\)”。电视机的大小是根据屏幕的对角线测量的，宽屏的长度大于宽度。屏幕的面积也为\(1728\)平方英寸。他的娱乐中心有一个电视插件，长度为\(50\)英寸，宽度\(40\)为英寸。电视屏幕的长度和宽度是多少？它适合罗曼的娱乐中心吗？
唐内特在车库拍卖会上找到了一台宽屏电视，但不确定它是否适合她的娱乐中心。电视是\(50\)”。电视机的大小是根据屏幕的对角线测量的，宽屏的长度大于宽度。屏幕的面积也为\(1200\)平方英寸。她的娱乐中心有一个电视插件，长度为\(38\)英寸，宽度\(27\)为英寸。电视屏幕的长度和宽度是多少？它适合 Donnette 的娱乐中心吗？

回答

2。 \(-3\)和\(14\)

4。 \(-7\)and\(-8\) 或 an\(8\) d\(7\)

6。 \(-6\)and\(-4\) or\(-6\) and\(4\) 或 an\(6\) d\(-4\) 或 an\(6\) d\(4\)

8。如果长度为\(11\) cm，则宽度为\(15\) cm。如果长度为\(15\) cm，则宽度为\(11\) cm。

10。如果长度为\(10\)英寸，则宽度为\(24\)英寸。如果长度为\(24\)英寸，则宽度为\(10\)英寸。

12。长度为\(40\)英寸，宽度为\(30\)英寸。电视不适合 Donnette 的娱乐中心。

练习\(\PageIndex{21}\) Writing Exercises

用你自己的话说，解释通过图表求解方程组的优缺点。
用你自己的话解释如何使用替换来求解方程组。
用你自己的话解释如何使用消除法求解方程组。
圆和抛物线可以以可能产生\(4\)解的方式相交。\(0, 1, 2, 3,\) 绘制每种可能性的草图。

回答

2。答案可能有所不同

4。答案可能有所不同

自检

a. 完成练习后，使用此清单评估您对本节目标的掌握程度。

此表有四列五行。第一行是标题，它标记了每列，“我可以”、“自信地”、“有帮助” 和 “不行”™ 不明白！ α€ 在第 2 行中，我能用图表求解非线性方程组。在第 3 行中，我可以使用替换求解非线性方程组。在第 4 行中，I can 是使用消除法求解非线性方程组。在第 5 行中，“我能” 是使用非线性方程组来求解应用程序。 — 图 11.5.67