11.6：求解非线性方程组

Last updated
Save as PDF

Page ID: 204358

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

学习目标

在本节结束时，您将能够：

使用图表求解非线性方程组
使用替换求解非线性方程组
使用消除法求解非线性方程组
使用非线性方程组来求解应用程序

在开始之前，请参加这个准备测验。

通过绘制图解系统:$\left\{\begin{array}{l}{x-3 y=-3} \\ {x+y=5}\end{array}\right.$.
如果你错过了这个问题，请查看示例 4.2。
通过替换求解系统：$\left\{\begin{array}{l}{x-4 y=-4} \\ {-3 x+4 y=0}\end{array}\right.$
如果你错过了这个问题，请查看示例 4.7。
通过淘汰解决系统：$\left\{\begin{array}{l}{3 x-4 y=-9} \\ {5 x+3 y=14}\end{array}\right.$
如果你错过了这个问题，请查看示例 4.9。

使用图形求解非线性方程组

我们学会了如何通过绘图、替换和消除来求解具有两个变量的线性方程组。我们将使用相同的方法来研究具有两个方程和两个变量的非线性方程组。 非线性方程组是指至少有一个方程不是线性的系统。

例如，以下每个系统都是非线性方程组。

$\left\{\begin{array}{l}{x^{2}+y^{2}=9} \\ {x^{2}-y=9}\end{array}\right. \left\{\begin{array}{l}{9 x^{2}+y^{2}=9} \\ {y=3 x-3}\end{array}\right. \left\{\begin{array}{l}{x+y=4} \\ {y=x^{2}+2}\end{array}\right.$

定义$\PageIndex{1}$

非线性方程组是指至少有一个方程不是线性的系统。

就像线性方程组一样，非线性系统的解是使两个方程都成真的有序对。在非线性系统中，可能有多个解。当我们通过绘图求解非线性方程组时，我们将看到这一点。

当我们求解线性方程组时，该系统的解是两条线的交点。对于非线性方程组，图可以是圆、抛物线或双曲线，可能有几个交点，因此有几个解。确定图表后，可视化图形可能相交的不同方式以及可能有多少解。

为了通过绘图求解非线性方程组，我们使用的步骤与针对非线性方程稍作修改的线性方程组的步骤基本相同。下面列出了这些步骤以供参考。

通过绘图求解非线性方程组。

确定每个方程的图形。绘制交叉点的可能选项。
绘制第一个方程的图形。
在同一个直角坐标系上绘制第二个方程的图形。
确定图形是否相交。
确定交叉点。
检查每个有序对是否是两个原始方程的解。

示例$\PageIndex{1}$

通过绘制图表求解系统：$\left\{\begin{array}{l}{x-y=-2} \\ {y=x^{2}}\end{array}\right.$

解决方案：

表 11.5.1
识别每张图表。	$\left\{\begin{array}{ll}{x-y=-2} & {\text { line }} \\ {y=x^{2}} & {\text { parabola }}\end{array}\right.$
绘制抛物线和直线交点的可能选项。	$。$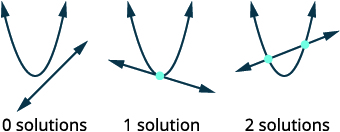
绘制线条图，$x-y=-2$。斜率截距形式$y=x+2$。绘制抛物线图，$y=x^{2}$。	$。$
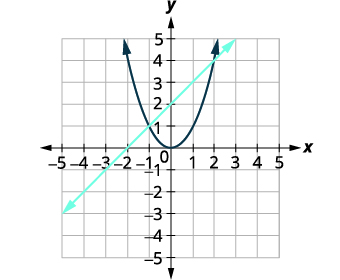确定交叉点。	交点似乎是$(2,3)$和$(-1,1)$。
检查以确保每个解都使两个方程都成立。 $(2,4)$ $\begin{array} {r l } {x-y=-2}\quad\quad {y=x^{2}} \\ {2-4\stackrel{?}{=}-2}\quad\quad {4\stackrel{?}{=}2^{2}} \\ {-2 = -2}\quad\quad\:{4 = 4} \end{array}$ $(-1,1)$ $\begin{array} {l l } {x-y=-2}\quad\quad {y=x^{2}} \\ {-1-1\stackrel{?}{=}-2}\:\quad {1\stackrel{?}{=}(-1)^{2}} \\ {-2 = -2}\quad\quad\quad{1 = 1} \end{array}$
	解决方案是$(2,4)$和$(-1,1)$。

练习$\PageIndex{1}$

通过绘制图解系统:$\left\{\begin{array}{l}{x+y=4} \\ {y=x^{2}+2}\end{array}\right.$.

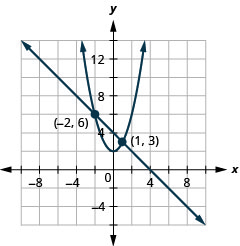
回答: $此图显示了系统的方程，x 加 y 等于 4，y 等于 x 平方加 2，x y 坐标平面。直线的斜率为负 1，Y 截距为 4。抛物线的顶点是 (0, 2)，向上打开。直线和抛物线在标注的点（负 2、6）和（1、3）处相交。$
图 11.5.3

练习$\PageIndex{2}$

通过绘制图表求解系统：$\left\{\begin{array}{l}{x-y=-1} \\ {y=-x^{2}+3}\end{array}\right.$

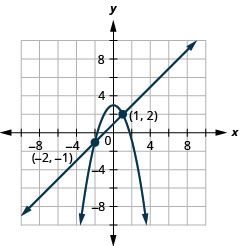
回答: $此图显示了系统的方程，x 减去 y 等于负 1，y 等于负 x 平方加三，x y 坐标平面。直线的斜率为 1，Y 截距为 1。抛物线的顶点是（0，负 3），向上打开。直线和抛物线在标注的点（负 2、负 1）和（1、2）处相交。$
图 11.5.4

要识别每个方程的图形，请记住每个圆锥$x^{2}$和$y^{2}$项的特征。

示例$\PageIndex{2}$

通过绘制图解系统:$\left\{\begin{array}{l}{y=-1} \\ {(x-2)^{2}+(y+3)^{2}=4}\end{array}\right.$.

解决方案：

表 11.5.2
识别每张图表。	$\left\{\begin{array}{ll}{y=-1} & {\text { line }} \\ {(x-2)^{2}+(y+3)^{2}=4} & {\text { circle }}\end{array}\right.$
绘制圆和直线交点的可能选项。	$。$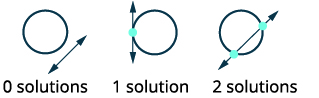
绘制圆圈图，$(x-2)^{2}+(y+3)^{2}=4$ 中心：$(2,-3)$半径：$2$ 绘制线条图，$y=-1$。这是一条水平线。	$。$
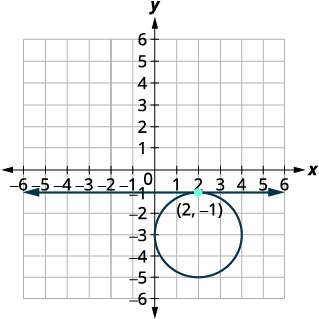确定交叉点。	交叉点似乎是$(2,-1)$。
检查以确保解使两个方程都成立。 $(2,-1)$ $\begin{array} {r r} {(x-2)^{2}+(y+3)^{2}=4} \quad\quad {y=-1} \\ {(2-2)^{2}+(-1+3)^{2}\stackrel{?}{=}4}\quad{-1=-1} \\ {(0)^{2}+(2)^{2}\stackrel{?}{=}4}\quad\quad\quad\quad\quad \\ {4=4}\quad\quad\quad\quad\quad \end{array}$
	解决方案是$(2,-1)$

练习$\PageIndex{3}$

通过绘制图表求解系统：$\left\{\begin{array}{l}{x=-6} \\ {(x+3)^{2}+(y-1)^{2}=9}\end{array}\right.$

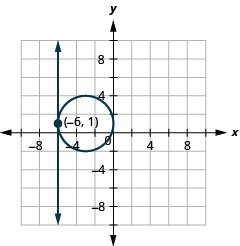
回答: $此图显示了一个系统的方程，x 等于负 6，数量 x 加 3 的平方加上量 y 减去 1 平方等于 x y 坐标平面上的 9，即一个圆。这条线是一条垂直线。圆的中心是（负 3, 1），其半径为 3 个单位。直线和圆之间的交点为（负 6, 1）。$
图 11.5.7

练习$\PageIndex{4}$

通过绘制图表求解系统：$\left\{\begin{array}{l}{y=4} \\ {(x-2)^{2}+(y+3)^{2}=4}\end{array}\right.$

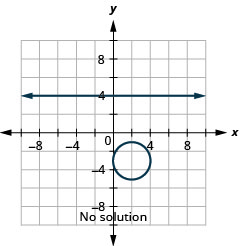
回答: $此图显示了一个系统的方程，y 等于负 4，量 x 减去 2 的平方加上量 y 加 3 的平方等于 x y 坐标平面上的 4，即一个圆。这条线是一条水平线。圆的中心是（2，负 3），其半径为 2 个单位。直线和圆之间没有交点，因此系统没有解。$
图 11.5.8

使用替换求解非线性方程组

当交点是整数并且易于从图表上读取时，绘图方法效果很好。但更多时候很难读出交点的坐标。替换方法是一种代数方法，在许多情况下都能很好地发挥作用。当很容易为其中一个变量求解其中一个方程时，它特别有效。

替换方法与我们在线性方程组中使用的替换方法非常相似。下面列出了这些步骤以供参考。

通过替换求解非线性方程组

确定每个方程的图形。绘制交叉点的可能选项。
求解任一变量的其中一个方程。
将步骤 2 中的表达式替换为另一个方程。
求解由此产生的方程。
将步骤 4 中的每个解替换为其中一个原始方程以找到另一个变量。
将每个解写成有序对。
检查每个有序对是否是两个原始方程的解。

示例$\PageIndex{3}$

使用替换求解系统：$\left\{\begin{array}{l}{9 x^{2}+y^{2}=9} \\ {y=3 x-3}\end{array}\right.$

解决方案：

表 11.5.3
识别每张图表。	$\left\{\begin{array}{ll}{9 x^{2}+y^{2}=9} & {\text { ellipse }} \\ {y=3 x-3} & {\text { line }}\end{array}\right.$
草绘椭圆和直线交点的可能选项。	$。$
该方程$y=3x-3$已求解$y$。	$。$
	$。$
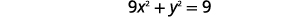在第一个方程$y$中替换$3x-3$。	$。$
求解方程式$x$。	$。$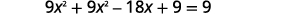
	$。$
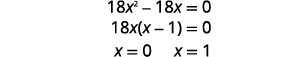替换$x=0$然后$x=1$进$y=3x-3$去找$y$-.	$。$
	$。$
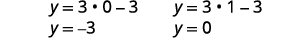	订购的货币对是$(0,-3), (1,0)$。
检查两个方程中的两个有序对。 $(0,-3)$ $\begin{array} {r l}{9 x^{2}+y^{2}=9} &\quad { y=3 x-3} \\ {9\cdot0^{2}+(-3)^{2}\stackrel{?}{=}9}&\quad{-3\stackrel{?}{=}3\cdot0-3} \\ {0+9\stackrel{?}{=}9}&\quad{-3\stackrel{?}{=}0-3} \\ {9=9}&\quad{-3=-3} \end{array}$ $(1,0)$ $\begin{array} {r l}{9 x^{2}+y^{2}=9} &\quad { y=3 x-3} \\ {9\cdot 1^{2}+(0)^{2}\stackrel{?}{=}9}&\quad{0\stackrel{?}{=}3\cdot 1-3} \\ {9+0\stackrel{?}{=}9}&\quad{0\stackrel{?}{=}3-3} \\ {9=9}&\quad{0=0} \end{array}$
	解决方案是$(0,-3), (1,0)$。

练习$\PageIndex{5}$

使用替换求解系统：$\left\{\begin{array}{l}{x^{2}+9 y^{2}=9} \\ {y=\frac{1}{3} x-3}\end{array}\right.$

回答: 没有解决办法

练习$\PageIndex{6}$

使用替换求解系统：$\left\{\begin{array}{l}{4 x^{2}+y^{2}=4} \\ {y=x+2}\end{array}\right.$

回答: $\left(-\frac{4}{5}, \frac{6}{5}\right),(0,2)$

到目前为止，每个非线性方程组都至少有一个解。下一个示例将显示另一个选项。

示例$\PageIndex{4}$

使用替换求解系统：$\left\{\begin{array}{l}{x^{2}-y=0} \\ {y=x-2}\end{array}\right.$

解决方案：

表 11.5.4
识别每张图表。	$\left\{\begin{array}{ll}{x^{2}-y=0} & {\text { parabola }} \\ {y=x-2} & {\text { line }}\end{array}\right.$
绘制抛物线和直线交点的可能选项。	$。$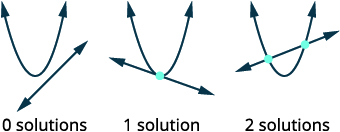
该方程$y=x-2$已求解$y$。	$。$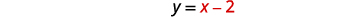
	$。$
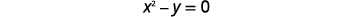在第一个方程$y$中替换$x-2$。	$。$
求解方程式$x$。	$。$
这不容易分解，所以我们可以检查判别值。
$\begin{array}{c}{b^{2}-4 a c} \\ {(-1)^{2}-4 \cdot 1 \cdot 2} \\ {-7}\end{array}$	判别是负数，所以没有真正的解决方案。系统没有解决办法。

练习$\PageIndex{7}$

使用替换求解系统：$\left\{\begin{array}{l}{x^{2}-y=0} \\ {y=2 x-3}\end{array}\right.$

回答: 没有解决办法

练习$\PageIndex{8}$

使用替换求解系统：$\left\{\begin{array}{l}{y^{2}-x=0} \\ {y=3 x-2}\end{array}\right.$

回答: $\left(\frac{4}{9},-\frac{2}{3}\right),(1,1)$

使用消除法求解非线性方程组

当我们研究线性方程组时，我们使用消除法来求解方程组。我们还可以使用消除来求解非线性方程组。当方程将两个变量平方时，它会很好地发挥作用。在使用消除时，我们尝试使一个变量的系数成为相反的系数，所以当我们将方程相加时，该变量就会被消除。

消除法与我们在线性方程组中使用的消除法非常相似。列出这些步骤以供参考。

通过消除求解方程组

确定每个方程的图形。绘制交叉点的可能选项。
用标准形式写下两个方程式。
使一个变量的系数成对立面。
决定要消除哪个变量。
将一个或两个方程相乘，使该变量的系数相对。
将步骤 3 得出的方程相加，以消除一个变量。
求解剩余变量。
将步骤 5 中的每个解替换为原始方程之一。然后求解另一个变量。
将每个解写成有序对。
检查每个有序对是否是两个原始方程的解。

示例$\PageIndex{5}$

通过消除来解决系统：$\left\{\begin{array}{l}{x^{2}+y^{2}=4} \\ {x^{2}-y=4}\end{array}\right.$

解决方案：

表 11.5.5
识别每张图表。	$。$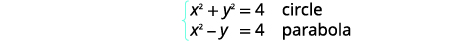
绘制圆形和抛物线交点的可能选项。	$。$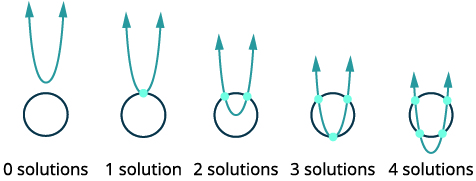
两个方程都是标准形式。	$。$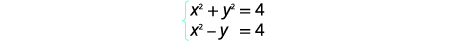
要获得相反的系数$x^{2}$，我们将第二个方程乘以$-1$。	$。$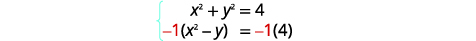
简化。	$。$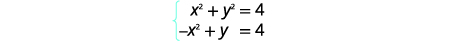
将两个方程相加以消除$x^{2}$/	$。$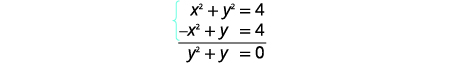
求解$y$。	$。$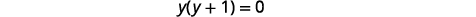
	$。$
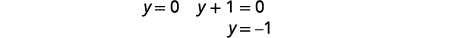$y=-1$将$y=0$和替换为原始方程之一。然后求解$x$。	$。$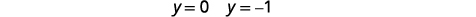
	$。$
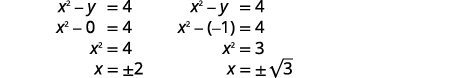将每个解写成有序对。	订购的货币对是$(-2,0)(2,0)$。 $(\sqrt{3},-1)(-\sqrt{3},-1)$
检查每个有序对是否是两个原始方程的解。
我们将把四种解决方案中的每一种的支票留给您。	解决方案是$(-2,0),(2,0),(\sqrt{3},-1)$、和$(-\sqrt{3},-1)$。

练习$\PageIndex{9}$

通过消除来解决系统：$\left\{\begin{array}{l}{x^{2}+y^{2}=9} \\ {x^{2}-y=9}\end{array}\right.$

回答: $(-3,0),(3,0),(-2 \sqrt{2},-1),(2 \sqrt{2},-1)$

练习$\PageIndex{10}$

通过消除来解决系统：$\left\{\begin{array}{l}{x^{2}+y^{2}=1} \\ {-x+y^{2}=1}\end{array}\right.$

回答: $(-1,0),(0,1),(0,-1)$

当我们考虑圆形和双曲线时，还有四个选项。

示例$\PageIndex{6}$

通过消除来解决系统：$\left\{\begin{array}{l}{x^{2}+y^{2}=7} \\ {x^{2}-y^{2}=1}\end{array}\right.$

解决方案：

表 11.5.6
识别每张图表。	$\left\{\begin{array}{ll}{x^{2}+y^{2}=7} & {\text { circle }} \\ {x^{2}-y^{2}=1} & {\text { hyperbola }}\end{array}\right.$
绘制圆形和双曲线交点的可能选项。	$。$
两个方程都是标准形式。	$\left\{\begin{array}{l}{x^{2}+y^{2}=7} \\ {x^{2}-y^{2}=1}\end{array}\right.$
的系数相反$y^{2}$，因此我们将添加方程。	$\left\{\begin{array}{l}{x^{2}+y^{2}=7} \\ {x^{2}-y^{2}=1}\end{array}\right.$ $2 x^{2}=8$
简化。	$x^{2}=4$ $x=\pm 2$ $x=2 \quad x=-2$
$x=-2$将$x=2$和替换为原始方程之一。然后求解$y$。	$\begin{array}{rl}{x^{2}+y^{2} = 7} &\quad { x^{2}+y^{2}=7} \\ {2^{2}+y^{2}=7} & \quad{(-2)^{2}+y^{2}=7} \\ {4+y^{2}=7} &\quad {4+y^{2}=7} \\ {y^{2}=3} &\quad {y^{2}=3} \\ {y=\pm \sqrt{3}} &\quad {y=\pm \sqrt{3}}\end{array}$
将每个解写成有序对。	有序的对是$(-2, \sqrt{3}),(-2,-\sqrt{3})$、$(2, \sqrt{3}),$和$(2,-\sqrt{3})$。
检查有序对是否是两个原始方程的解。
我们将把四种解决方案中的每一种的支票留给您。	解决方案是$(-2, \sqrt{3}),(-2,-\sqrt{3}),(2, \sqrt{3})$、和$(2,-\sqrt{3})$。

练习$\PageIndex{11}$

通过消除来解决系统：$\left\{\begin{array}{l}{x^{2}+y^{2}=25} \\ {y^{2}-x^{2}=7}\end{array}\right.$

回答: $(-3,-4),(-3,4),(3,-4),(3,4)$

练习$\PageIndex{12}$

通过消除来解决系统：$\left\{\begin{array}{l}{x^{2}+y^{2}=4} \\ {x^{2}-y^{2}=4}\end{array}\right.$

回答: $(-2,0),(2,0)$

使用非线性方程组来求解应用程序

非线性方程组可用于对许多应用程序进行建模和求解。我们将以每天的几何情况为例。

示例$\PageIndex{7}$

两个数字的平方之差为$15$。数字之和为$5$。找到数字。

解决方案：

表 11.5.7
确定我们在寻找什么。	两个不同的数字。
定义变量。	$x$=第一个数字 $y$=第二个数字
将信息转换为方程组。
第一句话。	两个数字的平方之差为$15$。
	$。$
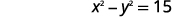第二句话。	数字之和为$5$。
	$。$
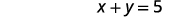通过替换求解系统。	$。$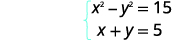
求解第二个方程$x$。	$。$
代$x$入第一个方程式。	$。$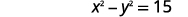
	$。$
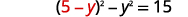扩展和简化。	$。$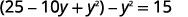
	$。$
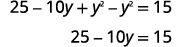求解$y$。	$。$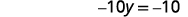
	$。$
替换回第二个方程式。	$。$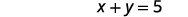
	$。$
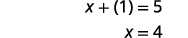	数字是$1$和$4$。

练习$\PageIndex{13}$

两个数字的平方之差为$−20$。数字之和为$10$。找到数字。

回答: $4$和$6$

练习$\PageIndex{14}$

两个数字的平方之差为$35$。数字之和为$−1$。找到数字。

回答: $-18$和$17$

示例$\PageIndex{8}$

迈拉为她的厨房购买了一台$25$ “小” 电视。电视的大小是在屏幕的对角线上测量的。屏幕的面积也为$300$平方英寸。电视屏幕的长度和宽度是多少？

解决方案：

表 11.5.8
确定我们在寻找什么。	矩形的长度和宽度。
定义变量。	Let$x$ = 矩形的宽度 $y$=矩形的长度
绘制图表以帮助可视化情况。	$。$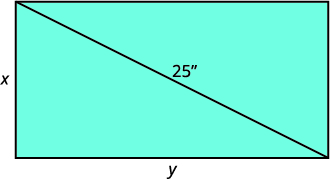
	面积为$300$平方英寸。
将信息转换为方程组。	直角三角形的对角线是$25$英寸。
	$。$
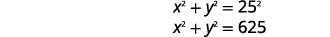	矩形的面积为$300$平方英寸。
	$。$
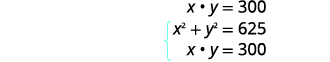使用替换求解系统。	$。$
求解第二个方程$x$。	$。$
代$x$入第一个方程式。	$。$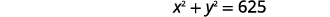
	$。$
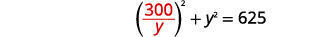简化。	$。$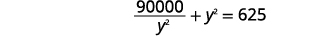
乘$y^{2}$以清除分数。	$。$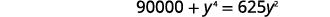
以标准形式放入。	$。$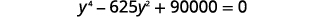
通过分解求解。	$。$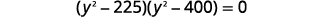
	$。$
	$。$
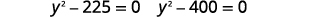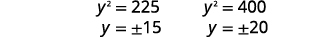由于$y$是矩形的一边，因此我们丢弃负值。	$。$
替换回第二个方程式。	$。$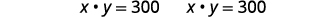
	$。$
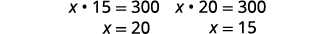	如果长度为$15$英寸，则宽度为$20$英寸。
	如果长度为$20$英寸，则宽度为$15$英寸。

练习$\PageIndex{15}$

埃德加为他的车库购买了一台$20$ “小” 电视。电视的大小是在屏幕的对角线上测量的。屏幕的面积也为$192$平方英寸。电视屏幕的长度和宽度是多少？

回答: 如果长度为$12$英寸，则宽度为$16$英寸。如果长度为$16$英寸，则宽度为$12$英寸。

练习$\PageIndex{16}$

哈珀一家人为他们的家庭房购买了一台小型微波炉。门的对角线长$15$度为英寸。门的面积也为$108$平方英寸。微波门的长度和宽度是多少？

回答: 如果长度为$12$英寸，则宽度为$9$英寸。如果长度为$9$英寸，则宽度为$12$英寸。

访问这些在线资源，获取有关求解非线性方程的更多说明和练习。

非线性方程组
求解非线性方程组
通过消除求解非线性方程组
非线性方程组——面积和周长应用

关键概念

如何通过绘图求解非线性方程组。
1. 确定每个方程的图形。绘制交叉点的可能选项。
2. 绘制第一个方程的图形。
3. 在同一个直角坐标系上绘制第二个方程的图形。
4. 确定图形是否相交。
5. 确定交叉点。
6. 检查每个有序对是否是两个原始方程的解。
如何通过替换求解非线性方程组。
1. 确定每个方程的图形。绘制交叉点的可能选项。
2. 求解任一变量的其中一个方程。
3. 将步骤 2 中的表达式替换为另一个方程。
4. 求解由此产生的方程。
5. 将步骤 4 中的每个解替换为其中一个原始方程以找到另一个变量。
6. 将每个解写成有序对。
7. 检查每个有序对是否是两个原始方程的解。
如何通过消除求解方程组。
1. 确定每个方程的图形。绘制交叉点的可能选项。
2. 用标准形式写下两个方程式。
3. 使一个变量的系数成对立面。
  决定要消除哪个变量。
  将一个或两个方程相乘，使该变量的系数相对。
4. 将步骤 3 得出的方程相加，以消除一个变量。
5. 求解剩余变量。
6. 将步骤 5 中的每个解替换为原始方程之一。然后求解另一个变量。
7. 将每个解写成有序对。
8. 检查每个有序对是否是两个原始方程的解。

识别每张图表。	\(\left\{\begin{array}{ll}{x^{2}+y^{2}=7} & {\text { circle }} \\ {x^{2}-y^{2}=1} & {\text { hyperbola }}\end{array}\right.\)
绘制圆形和双曲线交点的可能选项。	$。$
两个方程都是标准形式。	\(\left\{\begin{array}{l}{x^{2}+y^{2}=7} \\ {x^{2}-y^{2}=1}\end{array}\right.\)
的系数相反\(y^{2}\)，因此我们将添加方程。	\(\left\{\begin{array}{l}{x^{2}+y^{2}=7} \\ {x^{2}-y^{2}=1}\end{array}\right.\) \(2 x^{2}=8\)
简化。	\(x^{2}=4\) \(x=\pm 2\) \(x=2 \quad x=-2\)
\(x=-2\)将\(x=2\)和替换为原始方程之一。然后求解\(y\)。	\(\begin{array}{rl}{x^{2}+y^{2} = 7} &\quad { x^{2}+y^{2}=7} \\ {2^{2}+y^{2}=7} & \quad{(-2)^{2}+y^{2}=7} \\ {4+y^{2}=7} &\quad {4+y^{2}=7} \\ {y^{2}=3} &\quad {y^{2}=3} \\ {y=\pm \sqrt{3}} &\quad {y=\pm \sqrt{3}}\end{array}\)
将每个解写成有序对。	有序的对是\((-2, \sqrt{3}),(-2,-\sqrt{3})\)、\((2, \sqrt{3}),\)和\((2,-\sqrt{3})\)。
检查有序对是否是两个原始方程的解。
我们将把四种解决方案中的每一种的支票留给您。	解决方案是\((-2, \sqrt{3}),(-2,-\sqrt{3}),(2, \sqrt{3})\)、和\((2,-\sqrt{3})\)。

定义\(\PageIndex{1}\)

示例\(\PageIndex{1}\)

练习\(\PageIndex{1}\)

练习\(\PageIndex{2}\)

示例\(\PageIndex{2}\)

练习\(\PageIndex{3}\)

练习\(\PageIndex{4}\)

示例\(\PageIndex{3}\)

练习\(\PageIndex{5}\)

练习\(\PageIndex{6}\)

示例\(\PageIndex{4}\)

练习\(\PageIndex{7}\)

练习\(\PageIndex{8}\)

示例\(\PageIndex{5}\)

练习\(\PageIndex{9}\)

练习\(\PageIndex{10}\)

示例\(\PageIndex{6}\)

练习\(\PageIndex{11}\)

练习\(\PageIndex{12}\)

示例\(\PageIndex{7}\)

练习\(\PageIndex{13}\)

练习\(\PageIndex{14}\)

示例\(\PageIndex{8}\)

练习\(\PageIndex{15}\)

练习\(\PageIndex{16}\)

识别每张图表。	\(\left\{\begin{array}{ll}{x-y=-2} & {\text { line }} \\ {y=x^{2}} & {\text { parabola }}\end{array}\right.\)
绘制抛物线和直线交点的可能选项。	$。$
绘制线条图，\(x-y=-2\)。斜率截距形式\(y=x+2\)。绘制抛物线图，\(y=x^{2}\)。	$。$
确定交叉点。	交点似乎是\((2,3)\)和\((-1,1)\)。
检查以确保每个解都使两个方程都成立。 \((2,4)\) \(\begin{array} {r l } {x-y=-2}\quad\quad {y=x^{2}} \\ {2-4\stackrel{?}{=}-2}\quad\quad {4\stackrel{?}{=}2^{2}} \\ {-2 = -2}\quad\quad\:{4 = 4} \end{array}\) \((-1,1)\) \(\begin{array} {l l } {x-y=-2}\quad\quad {y=x^{2}} \\ {-1-1\stackrel{?}{=}-2}\:\quad {1\stackrel{?}{=}(-1)^{2}} \\ {-2 = -2}\quad\quad\quad{1 = 1} \end{array}\)
	解决方案是\((2,4)\)和\((-1,1)\)。

识别每张图表。	\(\left\{\begin{array}{ll}{y=-1} & {\text { line }} \\ {(x-2)^{2}+(y+3)^{2}=4} & {\text { circle }}\end{array}\right.\)
绘制圆和直线交点的可能选项。	$。$
绘制圆圈图，\((x-2)^{2}+(y+3)^{2}=4\) 中心：\((2,-3)\)半径：\(2\) 绘制线条图，\(y=-1\)。这是一条水平线。	$。$
确定交叉点。	交叉点似乎是\((2,-1)\)。
检查以确保解使两个方程都成立。 \((2,-1)\) \(\begin{array} {r r} {(x-2)^{2}+(y+3)^{2}=4} \quad\quad {y=-1} \\ {(2-2)^{2}+(-1+3)^{2}\stackrel{?}{=}4}\quad{-1=-1} \\ {(0)^{2}+(2)^{2}\stackrel{?}{=}4}\quad\quad\quad\quad\quad \\ {4=4}\quad\quad\quad\quad\quad \end{array}\)
	解决方案是\((2,-1)\)

识别每张图表。	\(\left\{\begin{array}{ll}{9 x^{2}+y^{2}=9} & {\text { ellipse }} \\ {y=3 x-3} & {\text { line }}\end{array}\right.\)
草绘椭圆和直线交点的可能选项。	$。$
该方程\(y=3x-3\)已求解\(y\)。	$。$
	$。$
在第一个方程\(y\)中替换\(3x-3\)。	$。$
求解方程式\(x\)。	$。$
	$。$
替换\(x=0\)然后\(x=1\)进\(y=3x-3\)去找\(y\)-.	$。$
	$。$
	订购的货币对是\((0,-3), (1,0)\)。
检查两个方程中的两个有序对。 \((0,-3)\) \(\begin{array} {r l}{9 x^{2}+y^{2}=9} &\quad { y=3 x-3} \\ {9\cdot0^{2}+(-3)^{2}\stackrel{?}{=}9}&\quad{-3\stackrel{?}{=}3\cdot0-3} \\ {0+9\stackrel{?}{=}9}&\quad{-3\stackrel{?}{=}0-3} \\ {9=9}&\quad{-3=-3} \end{array}\) \((1,0)\) \(\begin{array} {r l}{9 x^{2}+y^{2}=9} &\quad { y=3 x-3} \\ {9\cdot 1^{2}+(0)^{2}\stackrel{?}{=}9}&\quad{0\stackrel{?}{=}3\cdot 1-3} \\ {9+0\stackrel{?}{=}9}&\quad{0\stackrel{?}{=}3-3} \\ {9=9}&\quad{0=0} \end{array}\)
	解决方案是\((0,-3), (1,0)\)。

识别每张图表。	\(\left\{\begin{array}{ll}{x^{2}-y=0} & {\text { parabola }} \\ {y=x-2} & {\text { line }}\end{array}\right.\)
绘制抛物线和直线交点的可能选项。	$。$
该方程\(y=x-2\)已求解\(y\)。	$。$
	$。$
在第一个方程\(y\)中替换\(x-2\)。	$。$
求解方程式\(x\)。	$。$
这不容易分解，所以我们可以检查判别值。
\(\begin{array}{c}{b^{2}-4 a c} \\ {(-1)^{2}-4 \cdot 1 \cdot 2} \\ {-7}\end{array}\)	判别是负数，所以没有真正的解决方案。系统没有解决办法。