9.9: 求解二次不等式

Last updated
Save as PDF

Page ID: 204069

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

学习目标

在本节结束时，您将能够：

以图形方式求解二次不等式
用代数求解二次不等式

在开始之前，请参加这个准备测验。

解决：$2x−3=0$。
如果您错过了此问题，请查看示例 2.2。
解决：$2y^{2}+y=15$。
如果您错过了此问题，请查看示例 6.45。
Sol$\frac{1}{x^{2}+2 x-8}>0$
ve 如果你错过了这个问题，请查看示例 7.56。

我们之前已经学会了如何解决线性不等式和有理不等式。我们用来解决这些问题的一些技术是相同的，有些则不同。现在，我们将学会求解具有二次表达式的不等式。我们将使用一些求解线性和有理不等式以及二次方程的技术。我们将以两种方式求解二次不等式：图形和代数。

以图形方式求解二次不等式

二次方程在写成时为标准形式$ax^{2}+bx+c=0$。如果我们用不等号替换等号，则标准形式的二次不等式。

定义$\PageIndex{1}$: Quadratic Inequality

二次不等式是包含二次表达式的不等式。二次不等式的标准形式写成：

$\begin{array}{ll}{a x^{2}+b x+c<0} & {a x^{2}+b x+c \leq 0} \\ {a x^{2}+b x+c>0} & {a x^{2}+b x+c \geq 0}\end{array}$

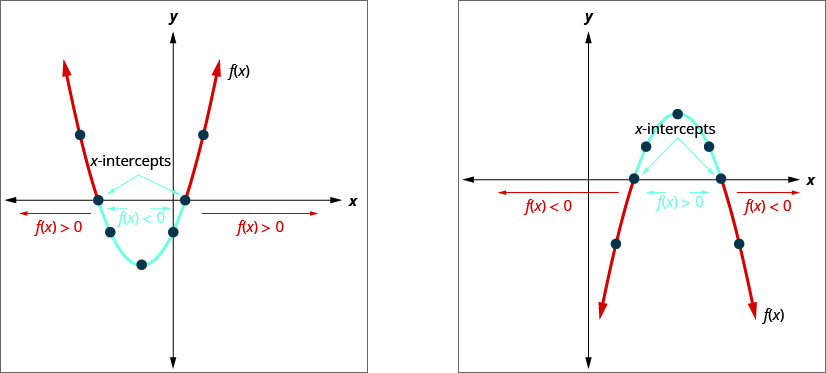
二次函数的图形$f(x)=a x^{2}+b x+c=0$是抛物线。当我们问什么时候是$a x^{2}+b x+c<0$，我们是在问什么时候是$f(x)<0$。我们想知道抛物线何时在$x$-轴以下。

当我们问什么时候是$a x^{2}+b x+c>0$，我们是在问什么时候是$f(x)>0$。我们想知道抛物线何时在$y$-轴上方。

第一张图是 x y 坐标平面上朝上的抛物线，即 x 的 f。在函数的左侧，x 的 f 大于 0。在 x 截距之间，x 的 f 小于 0。在函数的右侧，x 的 f 大于 0。第二张图是 x y 坐标平面上朝下的抛物线，即 x 的 f。在函数的左边，x 的 f 小于 0。在 x 截距之间，x 的 f 大于 0。在函数的右侧，x 的 f 小于 0。 — 图 9.8.1

示例$\PageIndex{1}$: How to Solve a Quadratic Inequality Graphically

$x^{2}−6x+8<0$以图形方式求解。用间隔表示法写出解。

解决方案：

第 1 步：以标准形式写下二次不等式。

不等式是标准形式。

$x^{2}-6 x+8<0$

第 2 步：$f(x)=a x^{2}+b x+c$使用属性或转换绘制函数图表。

我们将使用属性绘制图表。

$f(x)=x^{2}-6 x+8$

看看$a$方程式。

$\color{red}{a=1, b=-6, c=8}$

$f(x)=x^{2}-6 x+8$

由于$a$为正值，抛物线向上打开。

抛物线向上打开。

$f(x)=x^{2}-6 x+8$

对称轴是直线$x=-\frac{b}{2 a}$。

对称轴

$x=-\frac{b}{2 a}$

$\begin{array}{l}{x=-\frac{(-6)}{2 \cdot 1}} \\ {x=3}\end{array}$

对称轴是直线$x=3$。

顶点位于对称轴上。替换$x=3$到函数中。

顶点

$\begin{array}{l}{f(x)=x^{2}-6 x+8} \\ {f(3)=(\color{red}{3}\color{black}{)}^{2}-6(\color{red}{3}\color{black}{)}+8} \\ {f(3)=-1}\end{array}$

顶点是$(3,-1)$。

我们发现$f(0)$

$y$-截距

$\begin{array}{l}{f(x)=x^{2}-6 x+8} \\ {f(0)=(\color{red}{0}\color{black}{)}^{2}-6(\color{red}{0}\color{black}{)}+8} \\ {f(0)=8}\end{array}$

$y$-截距为$(0.8)$。

我们使用对称轴来找到一个与$y$-intercept对称的点。 $y$-截距是$3$指对称轴左边的单位$x=3$。对称轴右侧的点$3$单位有$x=6$。

指向对称$y$点到截距

重点是$(6,8)$。

我们解决$f(x)=0$。

$x$-拦截

我们可以通过分解来求解这个二次方程。

$\begin{aligned} f(x) &=x^{2}-6 x+8 \\ \color{red}{0} &\color{black}{=}x^{2}-6 x+8 \\ \color{red}{0} &\color{black}{=}(x-2)(x-4) \\ x &=2 \text { or } x=4 \end{aligned}$

$x$-intercepts 是$(2,0)$和$(4,0)$。

我们将顶点、截距和点绘制成与$y$-intercept对称的图形。我们将这些$5$点连接起来绘制抛物线。

第 3 步：根据图表确定解决方案。

$x^{2}-6 x+8<0$

不等式要求的值$x$使函数小于$0$。哪些值$x$使抛物线低于$x$-axis。

我们不包括这些值$2$，$4$因为不等式不只是不等式。

在区间表示法中，解是$(2,4)$。

练习$\PageIndex{1}$

用$x^{2}+2 x-8<0$图形求解
用间隔表示法写出解

回答

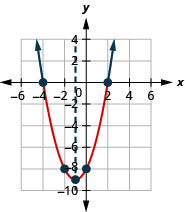
$此图显示了 x y 坐标平面上向上开口的抛物线。它的顶点为（负 2，负 9），y 截距为 (0, 8)，x 处显示的对称轴等于负 2。$
图 9.8.4
$(-4,2)$

练习$\PageIndex{2}$

用$x^{2}-8 x+12 \geq 0$图形求解
用间隔表示法写出解

回答

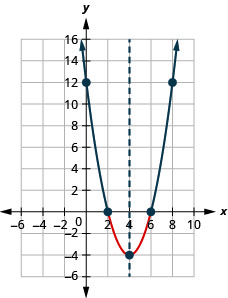
$此图显示了 x y 坐标平面上向上开口的抛物线。它的顶点为 (4，负 4)，x 截距为 (2, 0) 和 (6, 0)。$
图 9.8.5
$(-\infty, 2] \cup[6, \infty)$

我们以图形方式列出了解决二次不等式需要采取的步骤。

用图形求解二次不等式

用标准形式写下二次不等式。
绘制函数图表$f(x)=ax^{2}+bx+c$。
从图中确定解决方案。

在最后一个示例中，抛物线向上打开，在下一个示例中，抛物线向下打开。在这两种情况下，我们都在寻找抛物线中位于$x$-轴以下的部分，但要注意抛物线的位置如何影响解。

示例$\PageIndex{2}$

$-x^{2}-8 x-12 \leq 0$以图形方式求解。用间隔表示法写出解。

解决方案：

表 9.8.1
标准形式的二次不等式。	$-x^{2}-8 x-12 \leq 0$
绘制函数图表 $f(x)=-x^{2}-8 x-12$	抛物线向下打开。 $。$ 图 9.8.6
找到对称线。	$\begin{array}{l}{x=-\frac{b}{2 a}} \\ {x=-\frac{-8}{2(-1)}} \\ {x=-4}\end{array}$
找到顶点。	$\begin{aligned} f(x) &=-x^{2}-8 x-12 \\ f(-4) &=-(-4)^{2}-8(-4)-12 \\ f(-4) &=-16+32-12 \\ & f(-4)=4 \end{aligned}$ 顶点$(-4,4)$
找到$x$-截图。让$f(x)=0$。	$\begin{aligned} f(x) &=-x^{2}-8 x-12 \\ 0 &=-x^{2}-8 x-12 \end{aligned}$
系数：使用零乘积属性。	$\begin{array}{l}{0=-1(x+6)(x+2)} \\ {x=-6 \quad x=-2}\end{array}$
绘制抛物线图。	$x$-拦截$(-6,0), (-2.0)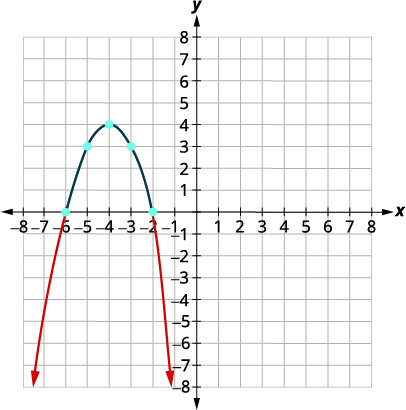$ $。$ 图 9.8.7
从图中确定解决方案。我们将$x$-intercepts包括在内，因为不等于 “小于或等于”。	$(-\infty,-6] \cup[-2, \infty)$

练习$\PageIndex{3}$

用$-x^{2}-6 x-5>0$图形求解
用间隔表示法写出解

回答

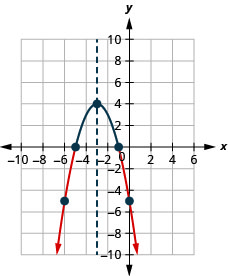
$x y 坐标平面上朝下的抛物线。它的顶点为（负 3，4），在（0，负 5）处的 y 截距，x 处显示的对称轴等于负 3。$
图 9.8.8
$(-5,-1)$

练习$\PageIndex{4}$

用$−x^{2}+10x−16≤0$图形求解
用间隔表示法写出解

回答

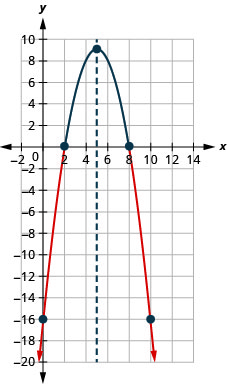
$x y 坐标平面上朝下的抛物线。它的顶点为 (5, 9)，Y 截距位于 (0，负 16)，对称轴为 x 等于 5。$
图 9.8.9
$(-\infty, 2] \cup[8, \infty)$

用代数求解二次不等式

我们将使用的代数方法与用于求解有理不等式的方法非常相似。我们将找到不等式的临界点，这将是相关二次方程的解。请记住，只有在表达式为零的情况下，多项式表达式才能改变符号。

我们将使用临界点将数字线划分为间隔，然后确定二次表达式在区间中是正数还是负数。然后，我们确定不平等的解决方案。

示例$\PageIndex{3}$: How to Solve Quadratic Inequalities Algebraically

用$x^{2}-x-12 \geq 0$代数求解。用间隔表示法写出解。

解决方案：

表 9.8.2
第 1 步：以标准形式写下二次不等式。	不等式是标准形式。	$x^{2}-x-12 \geq 0$
步骤 2：确定临界点——相关二次方程的解。	将不等号更改为等号，然后求解方程。	$\begin{array}{c}{x^{2}-x-12=0} \\ {(x+3)(x-4)=0} \\ {x+3=0 \quad x-4=0} \\ {x=-3 \quad x=4}\end{array}$
步骤 3：使用临界点将数字线划分为间隔。	使用$-3$和$4$将数字行划分为间隔。	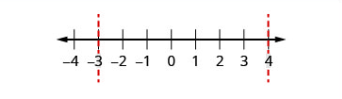$屏幕截图 (4) .png$
步骤 4：在数字线上方显示每个二次表达式的符号，使用取代原始不等式的每个区间的测试点。	测试： $x=-5$ $x=0$ $x=5$	$\begin{array}{ccc}{x^{2}-x-12} & {x^{2}-x-12} & {x^{2}-x-12} \\ {(-5)^{2}-(-5)-12} & {0^{2}-0-12} & {5^{2}-5-12} \\ {18} & {-12} & {8}\end{array}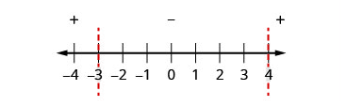$ $屏幕截图 (5) .png$ 图 9.8.11
步骤 5：确定不等式正确的间隔。用间隔表示法写出解。	$x^{2}-x-12 \geq 0$ 在第一个和最后一个间隔中，不等式为正，$0$在点处等于$-4,3$。	在区间表示法中，解是$(-\infty,-3] \cup[4, \infty)$。

练习$\PageIndex{5}$

用$x^{2}+2x−8≥0$代数求解。用间隔表示法写出解。

回答: $(-\infty,-4] \cup[2, \infty)$

练习$\PageIndex{6}$

用$x^{2}−2x−15≤0$代数求解。用间隔表示法写出解。

回答: $[-3,5]$

在这个例子中，由于表达式$x^{2}−x−12$因子很好，我们也可以在每个区间中找到符号，就像我们在求解有理不等式时所做的那样。我们找到每个因素的符号，然后找到产品的符号。我们的数字行是这样的：

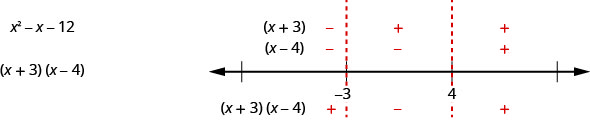
该图显示了表达式 x 的平方减去 x 减去 12 乘以 x 的数量加 3 乘以 x 的数量减去 4。该图显示了一条数字线，显示负数 3 和 4 上的虚线。它将数量 x 加 3 的符号显示为负、正、正，将数量 x 减去 4 的符号显示为负、负、正。在数字行下方，它显示数量 x 加 3 乘以数量 x 减 4，符号为正、负、正。 — 图 9.8.12

结果与我们使用另一种方法发现的结果相同。

我们在这里总结一下步骤。

用代数求解二次不等式

用标准形式写下二次不等式。
确定临界点——相关二次方程的解。
使用临界点将数字线划分为间隔。
数字线上方显示每个二次表达式的符号，使用每个区间的测试点替换为原始不等式。
确定不等式正确的时间间隔。用间隔表示法写出解。

示例$\PageIndex{4}$

用$x^{2}+6x−7≥0$代数求解。用间隔表示法写出解。

解决方案：

表 9.8.3
用标准形式写下二次不等式。	$-x^{2}+6 x-7 \geq 0$
将不等式的两边乘以$-1$。记得反转不等式符号。	$x^{2}-6 x+7 \leq 0$
通过求解相关的二次方程来确定临界点。	$x^{2}-6 x+7=0$
写下二次方程式。	$x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}$
然后替换为的值$a, b, c$。	$x=\frac{-(-6) \pm \sqrt{(-6)^{2}-4 \cdot 1 \cdot(7)}}{2 \cdot 1}$
简化。	$x=\frac{6 \pm \sqrt{8}}{2}$
简化激进。	$x=\frac{6 \pm 2 \sqrt{2}}{2}$
移除共同因素，$2$。	$\begin{array}{l}{x=\frac{2(3 \pm \sqrt{2})}{2}} \\ {x=3 \pm \sqrt{2}} \\ {x=3+\sqrt{2}} \quad x=3-\sqrt{2} \\ {x \approx 1.6}\quad\quad\:\:\: x\approx 4.4\end{array}$
使用临界点将数字线划分为间隔。检验原始不等式中每个间隔的数字。	$。$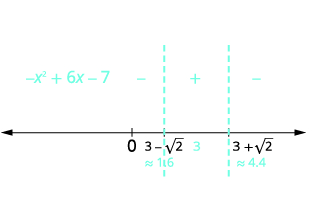
确定不等式正确的时间间隔。用间隔表示法写出解。	$-x^{2}+6 x-7 \geq 0$在中间间隔中$[3-\sqrt{2}, 3+\sqrt{2}]$

练习$\PageIndex{7}$

用$−x^{2}+2x+1≥0$代数求解。用间隔表示法写出解。

回答: $[-1-\sqrt{2},-1+\sqrt{2}]$

练习$\PageIndex{8}$

用$−x^{2}+8x−14<0$代数求解。用间隔表示法写出解。

回答: $(-\infty, 4-\sqrt{2}) \cup(4+\sqrt{2}, \infty)$

在前面的每个示例中，二次不等式的解要么是区间，要么是两个区间的并集。这是因为在每种情况下，我们都找到了相应二次方程的两个解$ax^{2}+bx+c=0$。然后，这两个解决方案为我们提供了两个$x$ —— 图形的截距，或者是将数字线划分为间隔的两个临界点。

这与我们之前关于使用判别的二次方程解的数目和类型的讨论相关。

对于形式的二次方程$ax^{2}+bc+c=0, a≠0$。

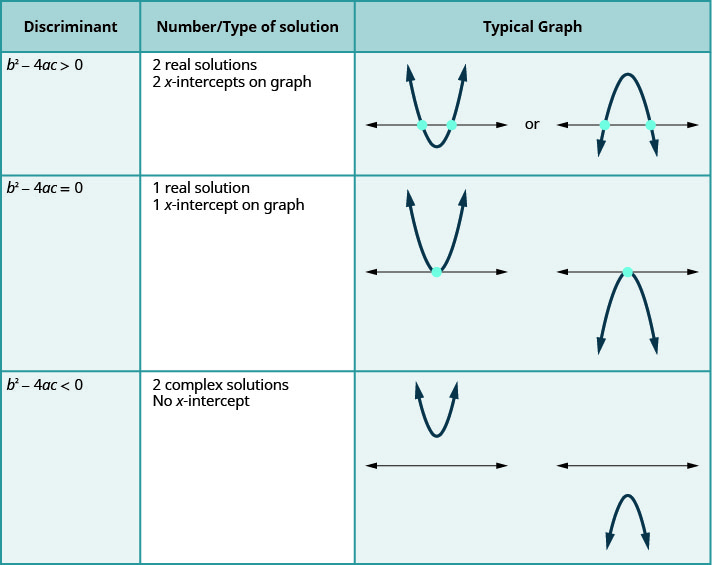
该图是一张包含 3 列的表格。第 1 列标记为判别法，第 2 列标记为解的数目/类型，第 3 列为典型图。横向读取，如果 b 平方减去 4 倍 a 乘以 c 大于 0，则会有 2 个实际解，因为图上有 2 个 x 截距。典型图形的图像是向上或向下的抛物线，有 2 个 x 截距。如果判别平方 b 减去 4 倍 a 乘以 c 等于 0，则有 1 个实解，因为图上有 1 个 x 截距。典型图形的图像是一个朝上或朝下的抛物线，其顶点位于 x 轴而不是穿过它。如果判别平方 b 减去 4 倍 a 乘以 c 小于 0，则有 2 个复解，因为没有 x 截距。典型图形的图像显示了朝上或朝下的抛物线，该抛物线不与 x 轴交叉。 — 图 9.8.14

表的最后一行显示了抛物线从不与$x$-轴相交的时间。使用二次公式求解二次方程，基数为负数。我们有两个复杂的解决方案。

在下一个示例中，二次不等式解将由二次方程的解为复数而产生。

示例$\PageIndex{5}$

求解，用区间表示法写出任何解：

$x^{2}-3 x+4>0$
$x^{2}-3 x+4 \leq 0$

解决方案：

一个。

表 9.8.4
用标准形式写下二次不等式。	$-x^{2}-3 x+4>0$
通过求解相关的二次方程来确定临界点。	$x^{2}-3 x+4=0$
写下二次方程式。	$x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}$
然后替换为的值$a, b, c$。	$x=\frac{-(-3) \pm \sqrt{(-3)^{2}-4 \cdot 1 \cdot(4)}}{2 \cdot 1}$
简化。	$x=\frac{3 \pm \sqrt{-7}}{2}$
简化 radicand。	$x=\frac{3 \pm \sqrt{7 i}}{2}$
复杂的解决方案告诉我们，抛物线不会拦截$x$-axis。此外，抛物线向上打开。这告诉我们抛物线完全高于$x$-axis。	复杂的解决方案 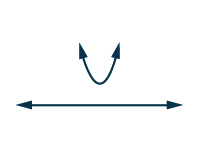$。$ 图 9.8.15

我们要找到解决的办法$x^{2}−3x+4>0$。由于图表的所有值都在$x$-axis上方，因此所有值都$x$使不等式成真。$x$ 我们用间隔表示法写$(−∞,∞)$。

b. 用标准形式写下二次不等式。

$x^{2}-3 x+4 \leq 0$

通过求解相关的二次方程来确定临界点。

$x^{2}-3 x+4=0$

由于相应的二次方程与 (a) 部分中的二次方程相同，因此抛物线将相同。抛物线向上打开，完全高于$x$-axis，其任何部分都不在$x$-axis 以下。

我们要找到解决的办法$x^{2}−3x+4≤0$。由于图表的所有$x$值永远不会低于$x$-axis，因此没有任何值$x$可以使不等式成真。没有办法解决不平等问题。

练习$\PageIndex{9}$

用区间表示法求解并写出任何解：

$-x^{2}+2 x-4 \leq 0$
$-x^{2}+2 x-4 \geq 0$

回答

$(-\infty, \infty)$
没有解决办法

练习$\PageIndex{10}$

用区间表示法求解并写出任何解：

$x^{2}+3 x+3<0$
$x^{2}+3 x+3>0$

回答

没有解决办法
$(-\infty, \infty)$

关键概念

用图形求解二次不等式
1. 用标准形式写下二次不等式。
2. $f(x)=ax^{2}+bx+c$使用属性或转换绘制函数图表。
3. 从图中确定解决方案。
如何用代数求解二次不等式
1. 用标准形式写下二次不等式。
2. 确定临界点——相关二次方程的解。
3. 使用临界点将数字线划分为间隔。
4. 数字线上方显示每个二次表达式的符号，使用每个区间的测试点替换为原始不等式。
5. 确定不等式正确的时间间隔。用间隔表示法写出解。

词汇表

二次不等式: 二次不等式是包含二次表达式的不等式。

标准形式的二次不等式。	\(-x^{2}-8 x-12 \leq 0\)
绘制函数图表 \(f(x)=-x^{2}-8 x-12\)	抛物线向下打开。 $。$ 图 9.8.6
找到对称线。	\(\begin{array}{l}{x=-\frac{b}{2 a}} \\ {x=-\frac{-8}{2(-1)}} \\ {x=-4}\end{array}\)
找到顶点。	\(\begin{aligned} f(x) &=-x^{2}-8 x-12 \\ f(-4) &=-(-4)^{2}-8(-4)-12 \\ f(-4) &=-16+32-12 \\ & f(-4)=4 \end{aligned}\) 顶点\((-4,4)\)
找到\(x\)-截图。让\(f(x)=0\)。	\(\begin{aligned} f(x) &=-x^{2}-8 x-12 \\ 0 &=-x^{2}-8 x-12 \end{aligned}\)
系数：使用零乘积属性。	\(\begin{array}{l}{0=-1(x+6)(x+2)} \\ {x=-6 \quad x=-2}\end{array}\)
绘制抛物线图。	\(x\)-拦截\((-6,0), (-2.0)\) $。$ 图 9.8.7
从图中确定解决方案。我们将\(x\)-intercepts包括在内，因为不等于 “小于或等于”。	\((-\infty,-6] \cup[-2, \infty)\)

用标准形式写下二次不等式。	\(-x^{2}+6 x-7 \geq 0\)
将不等式的两边乘以\(-1\)。记得反转不等式符号。	\(x^{2}-6 x+7 \leq 0\)
通过求解相关的二次方程来确定临界点。	\(x^{2}-6 x+7=0\)
写下二次方程式。	\(x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\)
然后替换为的值\(a, b, c\)。	\(x=\frac{-(-6) \pm \sqrt{(-6)^{2}-4 \cdot 1 \cdot(7)}}{2 \cdot 1}\)
简化。	\(x=\frac{6 \pm \sqrt{8}}{2}\)
简化激进。	\(x=\frac{6 \pm 2 \sqrt{2}}{2}\)
移除共同因素，\(2\)。	\(\begin{array}{l}{x=\frac{2(3 \pm \sqrt{2})}{2}} \\ {x=3 \pm \sqrt{2}} \\ {x=3+\sqrt{2}} \quad x=3-\sqrt{2} \\ {x \approx 1.6}\quad\quad\:\:\: x\approx 4.4\end{array}\)
使用临界点将数字线划分为间隔。检验原始不等式中每个间隔的数字。	$。$
确定不等式正确的时间间隔。用间隔表示法写出解。	\(-x^{2}+6 x-7 \geq 0\)在中间间隔中\([3-\sqrt{2}, 3+\sqrt{2}]\)

用标准形式写下二次不等式。	\(-x^{2}-3 x+4>0\)
通过求解相关的二次方程来确定临界点。	\(x^{2}-3 x+4=0\)
写下二次方程式。	\(x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\)
然后替换为的值\(a, b, c\)。	\(x=\frac{-(-3) \pm \sqrt{(-3)^{2}-4 \cdot 1 \cdot(4)}}{2 \cdot 1}\)
简化。	\(x=\frac{3 \pm \sqrt{-7}}{2}\)
简化 radicand。	\(x=\frac{3 \pm \sqrt{7 i}}{2}\)
复杂的解决方案告诉我们，抛物线不会拦截\(x\)-axis。此外，抛物线向上打开。这告诉我们抛物线完全高于\(x\)-axis。	复杂的解决方案 $。$ 图 9.8.15

定义\(\PageIndex{1}\): Quadratic Inequality

示例\(\PageIndex{1}\): How to Solve a Quadratic Inequality Graphically

练习\(\PageIndex{1}\)

练习\(\PageIndex{2}\)

示例\(\PageIndex{2}\)

练习\(\PageIndex{3}\)

练习\(\PageIndex{4}\)

示例\(\PageIndex{3}\): How to Solve Quadratic Inequalities Algebraically

练习\(\PageIndex{5}\)

练习\(\PageIndex{6}\)

示例\(\PageIndex{4}\)

练习\(\PageIndex{7}\)

练习\(\PageIndex{8}\)

示例\(\PageIndex{5}\)

练习\(\PageIndex{9}\)

练习\(\PageIndex{10}\)

第 1 步：以标准形式写下二次不等式。	不等式是标准形式。	\(x^{2}-x-12 \geq 0\)
步骤 2：确定临界点——相关二次方程的解。	将不等号更改为等号，然后求解方程。	\(\begin{array}{c}{x^{2}-x-12=0} \\ {(x+3)(x-4)=0} \\ {x+3=0 \quad x-4=0} \\ {x=-3 \quad x=4}\end{array}\)
步骤 3：使用临界点将数字线划分为间隔。	使用\(-3\)和\(4\)将数字行划分为间隔。	$屏幕截图 (4) .png$
步骤 4：在数字线上方显示每个二次表达式的符号，使用取代原始不等式的每个区间的测试点。	测试： \(x=-5\) \(x=0\) \(x=5\)	\(\begin{array}{ccc}{x^{2}-x-12} & {x^{2}-x-12} & {x^{2}-x-12} \\ {(-5)^{2}-(-5)-12} & {0^{2}-0-12} & {5^{2}-5-12} \\ {18} & {-12} & {8}\end{array}\) $屏幕截图 (5) .png$ 图 9.8.11
步骤 5：确定不等式正确的间隔。用间隔表示法写出解。	\(x^{2}-x-12 \geq 0\) 在第一个和最后一个间隔中，不等式为正，\(0\)在点处等于\(-4,3\)。	在区间表示法中，解是\((-\infty,-3] \cup[4, \infty)\)。