9.8E:练习
- Page ID
- 204103
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)
练习成就完美
在以下练习中,
- 在同一个矩形坐标系上绘制二次函数的图形
- 描述在函数中添加常量对基本抛物线有什么影响。\(k\)
- \(f(x)=x^{2}, g(x)=x^{2}+4, \text { and } h(x)=x^{2}-4\)
- \(f(x)=x^{2}, g(x)=x^{2}+7, \text { and } h(x)=x^{2}-7\)
- 回答
-
1。
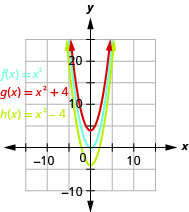
图 9.7.71- 的\(g(x)=x^{2}+4\)图形与单位的图形相同,\(f(x)=x^{2}\)但\(4\)单位向上移动。 的图形\(h(x)=x^{2}-4\)与单位的图形相同,\(f(x)=x^{2}\)但\(4\)单位向下移动。
在以下练习中,使用垂直移位绘制每个函数的图表。
- \(f(x)=x^{2}+3\)
- \(f(x)=x^{2}-7\)
- \(g(x)=x^{2}+2\)
- \(g(x)=x^{2}+5\)
- \(h(x)=x^{2}-4\)
- \(h(x)=x^{2}-5\)
- 回答
-
1。
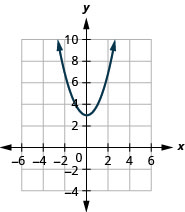
图 9.7.72 3。
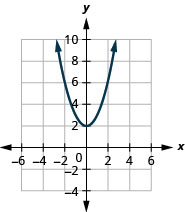
图 9.7.73 5。
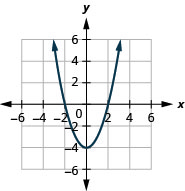
图 9.7.74
在以下练习中,
- 在同一个矩形坐标系上绘制二次函数的图形
- 描述在圆括号内添加常量会产生什么效果\(h\)
- \(f(x)=x^{2}, g(x)=(x-3)^{2}, \text { and } h(x)=(x+3)^{2}\)
- \(f(x)=x^{2}, g(x)=(x+4)^{2}, \text { and } h(x)=(x-4)^{2}\)
- 回答
-
1。
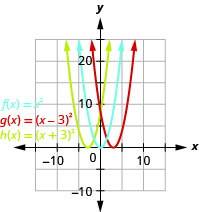
图 9.7.75- 的图形\(g(x)=(x−3)^{2}\)与图形相同,\(f(x)=x^{2}\)但\(3\)单位向右移动。 的图形\(h(x)=(x+3)^{2}\)与图形相同,\(f(x)=x^{2}\)但向左移动了\(3\)单位。
在以下练习中,使用水平移位绘制每个函数的图表。
- \(f(x)=(x-2)^{2}\)
- \(f(x)=(x-1)^{2}\)
- \(f(x)=(x+5)^{2}\)
- \(f(x)=(x+3)^{2}\)
- \(f(x)=(x-5)^{2}\)
- \(f(x)=(x+2)^{2}\)
- 回答
-
1。
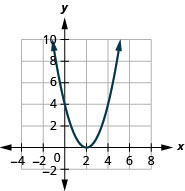
图 9.7.76 3。
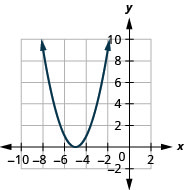
图 9.7.77 5。
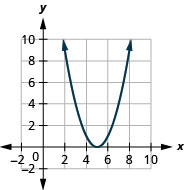
图 9.7.78
在以下练习中,使用转换绘制每个函数的图表。
- \(f(x)=(x+2)^{2}+1\)
- \(f(x)=(x+4)^{2}+2\)
- \(f(x)=(x-1)^{2}+5\)
- \(f(x)=(x-3)^{2}+4\)
- \(f(x)=(x+3)^{2}-1\)
- \(f(x)=(x+5)^{2}-2\)
- \(f(x)=(x-4)^{2}-3\)
- \(f(x)=(x-6)^{2}-2\)
- 回答
-
1。
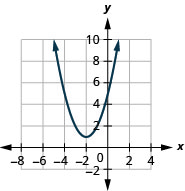
图 9.7.79 3。
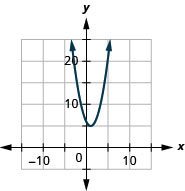
图 9.7.80 5。
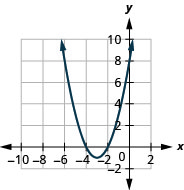
图 9.7.81 7。
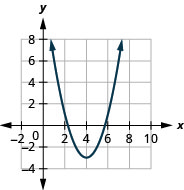
图 9.7.82
在以下练习中,绘制每个函数的图表。
- \(f(x)=-2 x^{2}\)
- \(f(x)=4 x^{2}\)
- \(f(x)=-4 x^{2}\)
- \(f(x)=-x^{2}\)
- \(f(x)=\frac{1}{2} x^{2}\)
- \(f(x)=\frac{1}{3} x^{2}\)
- \(f(x)=\frac{1}{4} x^{2}\)
- \(f(x)=-\frac{1}{2} x^{2}\)
- 回答
-
1。
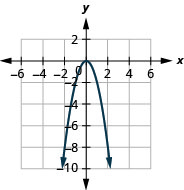
图 9.7.83 3。
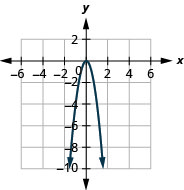
图 9.7.84 5。
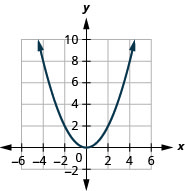
图 9.7.85 7。
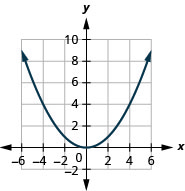
图 9.7.86
在以下练习中,通过填写正方\(f(x)=a(x−h)^{2}+k\)形来重写表单中的每个函数。
- \(f(x)=-3 x^{2}-12 x-5\)
- \(f(x)=2 x^{2}-12 x+7\)
- \(f(x)=3 x^{2}+6 x-1\)
- \(f(x)=-4 x^{2}-16 x-9\)
- 回答
-
1。 \(f(x)=-3(x+2)^{2}+7\)
3。 \(f(x)=3(x+1)^{2}-4\)
在以下练习中,
- 以\(f(x)=a(x−h)^{2}+k\)表单重写每个函数
- 使用转换将其绘制成图形
- \(f(x)=x^{2}+6 x+5\)
- \((x)=x^{2}+4 x-12\)
- \(f(x)=x^{2}+4 x-12\)
- \(f(x)=x^{2}-6 x+8\)
- \(f(x)=x^{2}-6 x+15\)
- \(f(x)=x^{2}+8 x+10\)
- \(f(x)=-x^{2}+8 x-16\)
- \(f(x)=-x^{2}+2 x-7\)
- \(f(x)=-x^{2}-4 x+2\)
- \(f(x)=-x^{2}+4 x-5\)
- \(f(x)=5 x^{2}-10 x+8\)
- \(f(x)=3 x^{2}+18 x+20\)
- \(f(x)=2 x^{2}-4 x+1\)
- \(f(x)=3 x^{2}-6 x-1\)
- \(f(x)=-2 x^{2}+8 x-10\)
- \(f(x)=-3 x^{2}+6 x+1\)
- 回答
-
1。
- f (x) = (x+3) ^ {2} -4
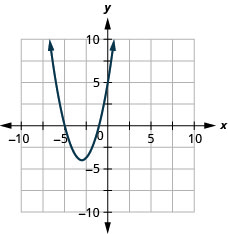
图 9.7.87 3。
- \(f(x)=(x+2)^{2}-1\)
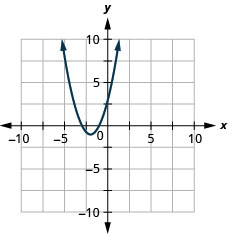
图 9.7.88 5。
- \(f(x)=(x-3)^{2}+6\)
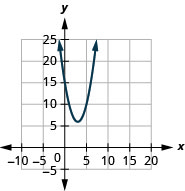
图 9.7.89 7。
- \(f(x)=-(x-4)^{2}+0\)
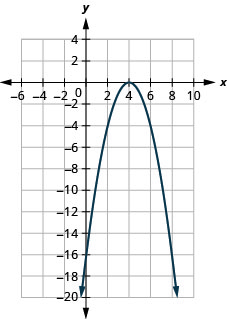
图 9.7.90 9。
- \(f(x)=-(x+2)^{2}+6\)
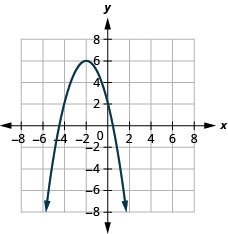
图 9.7.91 11。
- \(f(x)=5(x-1)^{2}+3\)
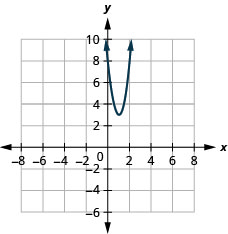
图 9.7.92 13。
- \(f(x)=2(x-1)^{2}-1\)
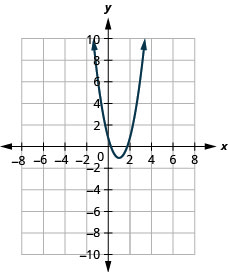
图 9.7.93 15。
- \(f(x)=-2(x-2)^{2}-2\)
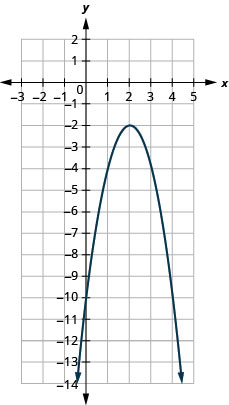
图 9.7.94
在以下练习中,
- 以\(f(x)=a(x−h)^{2}+k\)表单重写每个函数
- 使用属性绘制图表
- \(f(x)=2 x^{2}+4 x+6\)
- \(f(x)=3 x^{2}-12 x+7\)
- \(f(x)=-x^{2}+2 x-4\)
- \(f(x)=-2 x^{2}-4 x-5\)
- 回答
-
1。
- \(f(x)=2(x+1)^{2}+4\)
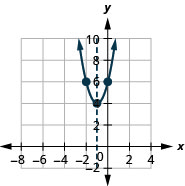
图 9.7.95 3。
- \(f(x)=-(x-1)^{2}-3\)
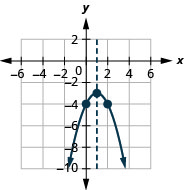
图 9.7.96
在以下练习中,将图表与以下函数之一进行匹配:
- \(f(x)=x^{2}+4\)
- \(f(x)=x^{2}-4\)
- \(f(x)=(x+4)^{2}\)
- \(f(x)=(x-4)^{2}\)
- \(f(x)=(x+4)^{2}-4\)
- \(f(x)=(x+4)^{2}+4\)
- \(f(x)=(x-4)^{2}-4\)
- \(f(x)=(x-4)^{2}+4\)
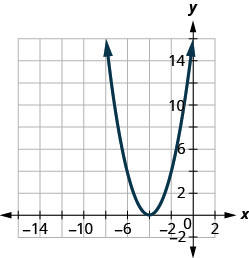
图 9.7.97
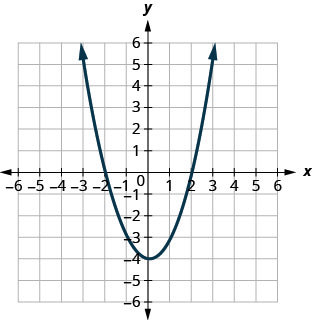
图 9.7.98
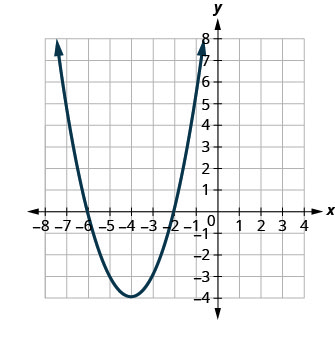
图 9.7.99
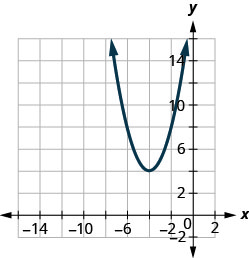
图 9.7.100
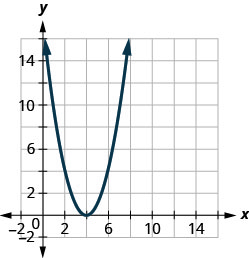
图 9.7.101
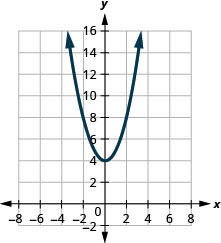
图 9.7.102
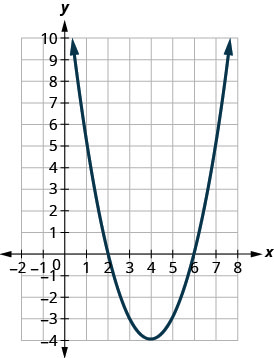
图 9.7.103
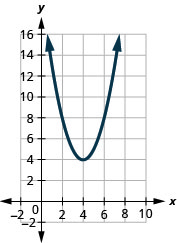
图 9.7.104
- 回答
-
1. c
3. e
5. d
7.g
在以下练习中,以显示图形的\(f(x)=a(x−h)^{2}+k\)形式编写二次函数。
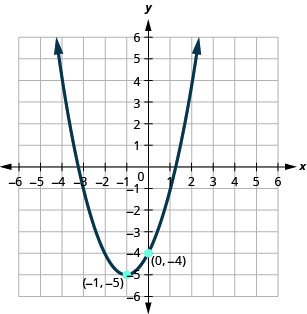
图 9.7.105
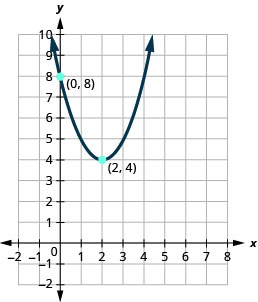
图 9.7.106
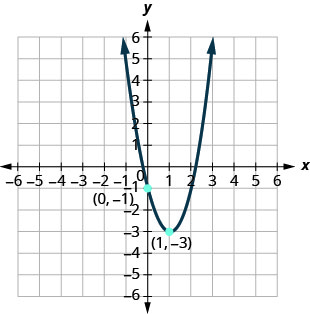
图 9.7.107
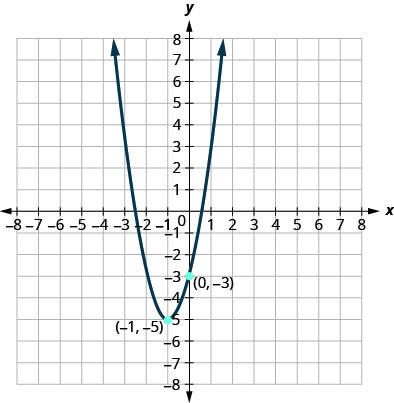
图 9.7.108
- 回答
-
1。 \(f(x)=(x+1)^{2}-5\)
3。 \(f(x)=2(x-1)^{2}-3\)
- 像我们在上一节中所做的那样,\(f(x)=x^{2}+4x+5\)首先使用属性绘制二次函数的图形,然后使用转换将其绘制成图形。 你更喜欢哪种方法? 为什么?
- 像我们在上一节中所做的那样,\(f(x)=2x^{2}−4x−3\)首先使用属性绘制二次函数的图形,然后使用转换将其绘制成图形。 你更喜欢哪种方法? 为什么?
- 回答
-
1。 答案可能有所不同。
自检
a. 完成练习后,使用此清单评估您对本节目标的掌握程度。
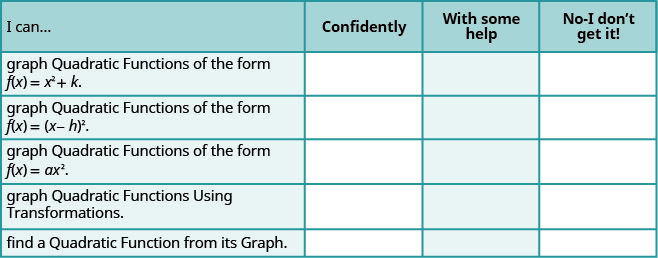
b. 看完清单后,你认为你为下一节做好了充分的准备吗? 为什么或者为什么不呢?


