9.8:使用变换绘制二次函数图
- Page ID
- 204091
在本节结束时,您将能够:
- 图形形式的二次函数\(f(x)=x^{2}+k\)
- 图形形式的二次函数\(f(x)=(x−h)^{2}\)
- 图形形式的二次函数\(f(x)=ax^{2}\)
- 使用变换绘制二次函数的图形
- 从其图形中找到二次函数
在开始之前,请参加这个准备测验。
- \(f(x)=x^{2}\)通过绘制点来绘制函数图表。
如果你错过了这个问题,请查看示例 3.54。 - 完全考虑因素:\(y^{2}−14y+49\).
如果您错过了此问题,请查看示例 6.24。 - 完全考虑因素:\(2x^{2}−16x+32\).
如果您错过了此问题,请查看示例 6.26。
绘制表格的二次函数\(f(x)=x^{2}+k\)
在上一节中,我们学习了如何使用二次函数的属性绘制二次函数的图形。 另一种方法是从基本图开始,\(f(x)=x^{2}\)然后根据函数方程中给出的信息 “移动” 它。 我们称之为使用变换绘制二次函数。
在第一个示例中,我们将\(f(x)=x^{2}\)通过绘制点来绘制二次函数的图形。 然后我们将看看在方程中添加一个常量会对新函数的图形产生什么影响\(f(x)=x^{2}+k\)。\(k\)
在同一个直角坐标系\(h(x)=x^{2}−2\)上绘制图\(f(x)=x^{2}\)形\(g(x)=x^{2}+2\)、和。 描述在函数中添加常量对基本抛物线有什么影响。
解决方案:
绘制点将帮助我们看到常量对基本\(f(x)=x^{2}\)图的影响。 我们填写所有三个函数的图表。
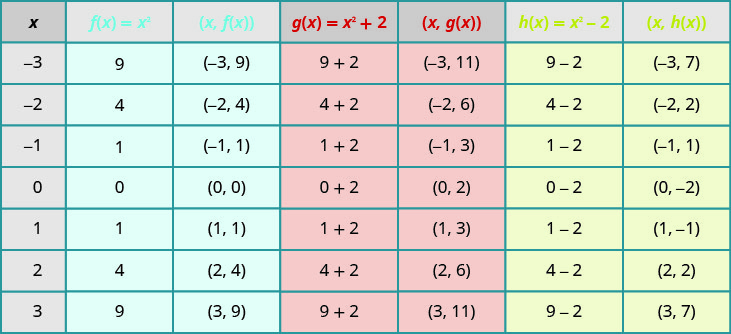
这些\(g(x)\)值比这些\(f(x)\)值多两个。 此外,这些\(h(x)\)值比这些值小两个。\(f(x)\) 现在,我们将在同一个直角坐标系上绘制所有三个函数的图形。
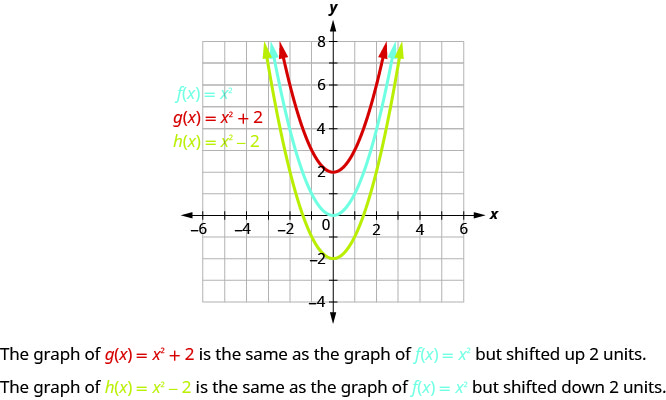
的\(g(x)=x^{2}+2\)图形与单位的图形相同,\(f(x)=x^{2}\)但\(2\)单位向上移动。
的图形\(h(x)=x^{2}−2\)与单位的图形相同,\(f(x)=x^{2}\)但\(2\)单位向下移动。
- 在同一个直角坐标系\(h(x)=x^{2}-1\)上绘制图\(f(x)=x^{2}, g(x)=x^{2}+1,\)形。
- 描述在函数中添加常量对基本抛物线有什么影响。
- 回答
-
一个。
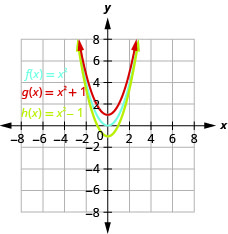
图 9.7.3 b. 的图形与单位的\(g(x)=x^{2}+1\)图形相同,\(f(x)=x^{2}\)但\(1\)单位向上移动。 的图形\(h(x)=x^{2}−1\)与图形相同,\(f(x)=x^{2}\)但\(1\)单位向下移动。
- 在同一个直角坐标系\(h(x)=x^{2}-6\)上绘制图\(f(x)=x^{2}, g(x)=x^{2}+6,\)形。
- 描述在函数中添加常量对基本抛物线有什么影响。
- 回答
-
一个。
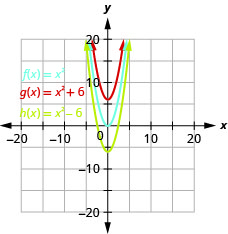
图 9.7.4 b. 的图形与单位的\(h(x)=x^{2}+6\)图形相同,\(f(x)=x^{2}\)但\(6\)单位向上移动。 的图形\(h(x)=x^{2}-6\)与单位的图形相同,\(f(x)=x^{2}\)但\(6\)单位向下移动。
最后一个例子向我们表明,要绘制这种形式的二次函数\(f(x)=x^{2}+k\),我们采用基本的抛物线图,\(f(x)=x^{2}\)然后将其垂直向上移动\((k>0)\)或向下移动\((k<0)\)。
这种变换称为垂直移动。
\(f(x)=x^{2}+k\)使用垂直移位绘制形状的二次函数
的图表会\(f(x)=x^{2}+k\)移动\(f(x)=x^{2}\)垂直\(k\)单位的图形。
- 如果是\(k>0\),则将抛物线垂直向上移动\(k\)单位。
- 如果为\(k<0\),则将抛物线垂直向下移动\(|k|\)单位。
既然我们已经看到了常数的效果\(k\),就可以很容易地绘制出这种形式的函数\(f(x)=x^{2}+k\)了。 我们从基本的抛物线开始,\(f(x)=x^{2}\)然后将其向上或向下移动。
\(f(x)=x^{2}\)快速练习素描可能会有所帮助。 我们知道这些值,可以从那里绘制图表。
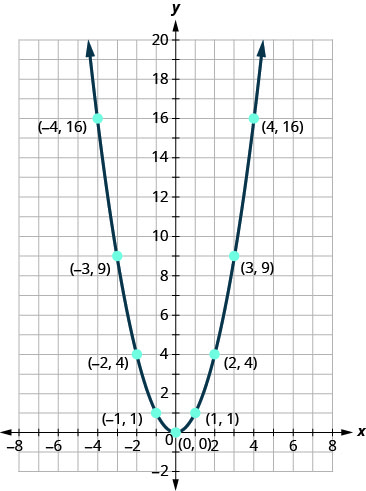
一旦我们知道了这个抛物线,就可以很容易地应用变换了。 下一个示例需要垂直移动。
\(f(x)=x^{2}−3\)使用垂直移位绘制图表。
解决方案:
| 我们首先在网格\(f(x)=x^{2}\)上画出图形。 | 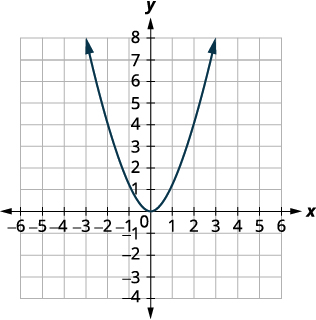 |
| 确定\(k\)。 | 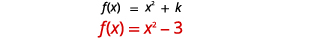 |
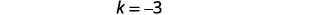 |
|
| \(f(x)=x^{2}\)向下移动图表\(3\)。 | 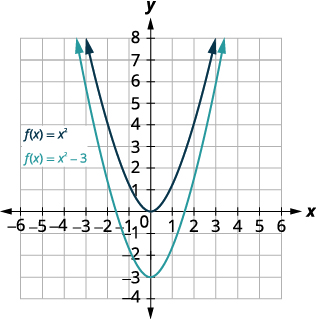 |
\(f(x)=x^{2}−5\)使用垂直移位绘制图表。
- 回答
-
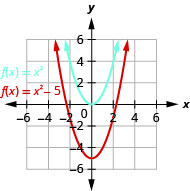
图 9.7.10
\(f(x)=x^{2}+7\)使用垂直移位绘制图表。
- 回答
-
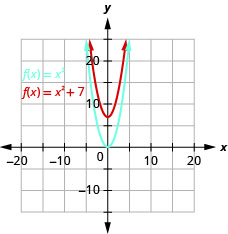
图 9.7.11
绘制表格的二次函数\(f(x)=(x-h)^{2}\)
在第一个示例中,我们\(f(x)=x^{2}\)通过绘制点来绘制二次函数的图形,然后看到\(k\)向该函数添加一个常量对新函数生成的图形产生的影响\(f(x)=x^{2}+k\)。
现在,我们将探讨从 has 中减去一个常量\(x\)对新函数生成的图的影响\(f(x)=(x−h)^{2}\)。\(h\)
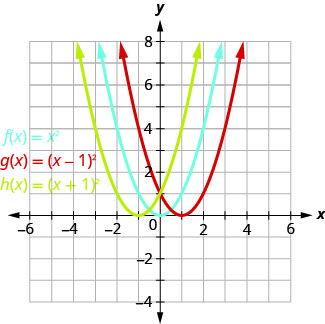
在同一个直角坐标系\(h(x)=(x+1)^{2}\)上绘制图\(f(x)=x^{2}, g(x)=(x-1)^{2},\)形。 描述在函数中添加常量对基本抛物线有什么影响。
解决方案:
绘制点将帮助我们看到常量对基本\(f(x)=x^{2}\)图的影响。 我们填写所有三个函数的图表。
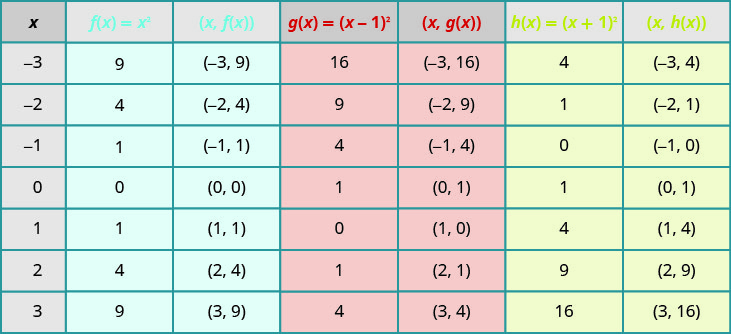
这些\(g(x)\)值和\(h(x)\)值共享共同的数字\(0, 1, 4, 9\)\(16\),但会被移动。

- 在同一个直角坐标系\(h(x)=(x-2)^{2}\)上绘制图\(f(x)=x^{2}, g(x)=(x+2)^{2},\)形。
- 描述在函数中添加常量对基本抛物线有什么影响。
- 回答
-
一个。
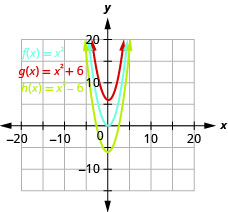
图 9.7.15 b. 的\(g(x)=(x+2)^{2}\)图形与\(2\)单位向左移动\(f(x)=x^{2}\)的图形相同。 的\(h(x)=(x−2)^{2}\)图形与单位的图形相同,\(f(x)=x^{2}\)但\(2\)单位向右移动。
- 在同一个直角坐标系\(h(x)=x^{2}-5\)上绘制图\(f(x)=x^{2}, g(x)=x^{2}+5,\)形。
- 描述在函数中添加常量对基本抛物线有什么影响。
- 回答
-
一个。
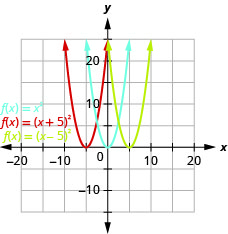
图 9.7.16 b. 的\(g(x)=(x+5)^{2}\)图形与\(5\)单位向左移动\(f(x)=x^{2}\)的图形相同。 的图形\(h(x)=(x-5)^{2}\)与图形相同,\(f(x)=x^{2}\)但\(5\)单位向右移动。
最后一个例子向我们表明,要绘制这种形式的二次函数\(f(x)=(x−h)^{2}\),我们取基本的抛物线图,\(f(x)=x^{2}\)然后向左移动\((h>0)\)或向右移动\((h<0)\)。
这种变换称为水平移动。
\(f(x)=(x-h)^{2}\)使用水平移位绘制表格的二次函数
的图表会\(f(x)=(x-h)^{2}\)移动\(f(x)=x^{2}\)水平\(h\)单位的图形。
- 如果是\(h>0\),则将抛物线水平向左移动\(h\)单位。
- 如果是\(h<0\),则将抛物线水平向右移动\(|h|\)单位。
既然我们已经看到了常数的效果\(h\),就可以很容易地绘制出这种形式的函数\(f(x)=(x−h)^{2}\)了。 我们从基本的抛物线开始,\(f(x)=x^{2}\)然后向左或向右移动。
下一个示例需要水平移动。
\(f(x)=(x−6)^{2}\)使用水平移位绘制图表。
解决方案:
| 我们首先在网格\(f(x)=x^{2}\)上画出图形。 | 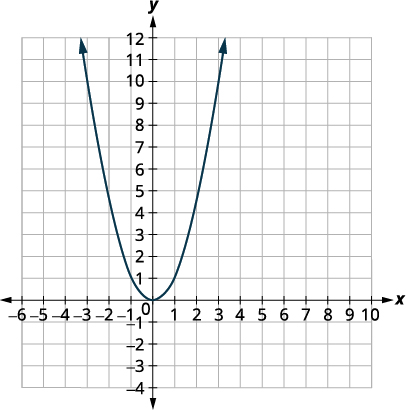 |
| 确定\(h\)。 | 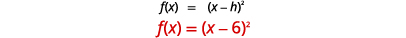 |
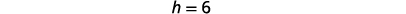 |
|
| 将图表移动\(f(x)=x^{2}\)到右边的\(6\)单位。 | 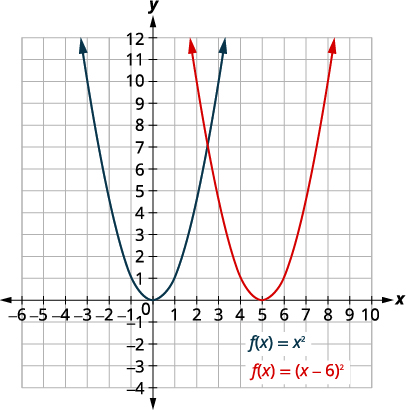 |
\(f(x)=(x−4)^{2}\)使用水平移位绘制图表。
- 回答
-
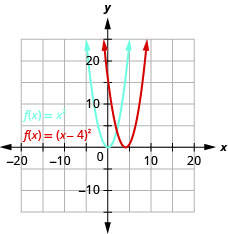
图 9.7.21
\(f(x)=(x+6)^{2}\)使用水平移位绘制图表。
- 回答
-
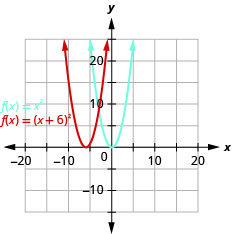
图 9.7.22
现在我们知道了常数\(h\)的效果\(k\),我们将绘制形态的二次函数,\(f(x)=(x-h)^{2}+k\)首先绘制基本抛物线,然后进行水平移动,然后进行垂直移动。 我们可以先进行垂直移动,然后进行水平移动,但是大多数学生更喜欢水平移动,然后是垂直移动。
\(f(x)=(x+1)^{2}-2\)使用转换绘制图表。
解决方案:
这个函数将涉及两个转换,我们需要一个计划。
让我们先确定常量\(h, k\)。
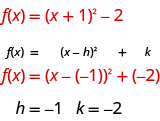
\(h\)常数给我们一个水平移动,\(k\)给我们一个垂直移动。
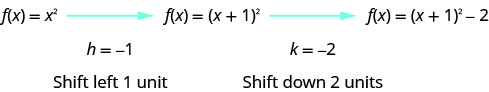
我们首先在网格\(f(x)=x^{2}\)上画出图形。

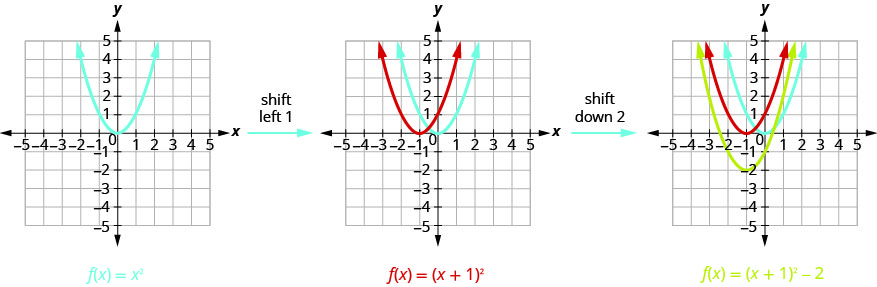
\(f(x)=(x+2)^{2}-3\)使用转换绘制图表。
- 回答
-
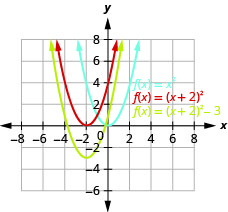
图 9.7.27
\(f(x)=(x-3)^{2}+1\)使用转换绘制图表。
- 回答
-
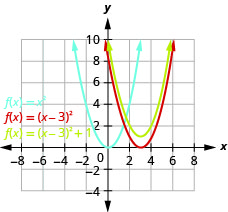
图 9.7.28
绘制表格的二次函数\(f(x)=ax^{2}\)
到目前为止,我们绘制了二次函数的图形,\(f(x)=x^{2}\)然后看到了在方程中包含一个常数\(h\)或\(k\)在方程中对新函数生成的图形产生的影响。 现在,我们将探讨系\(a\)数对新函数生成的图形的影响\(f(x)=ax^{2}\)。
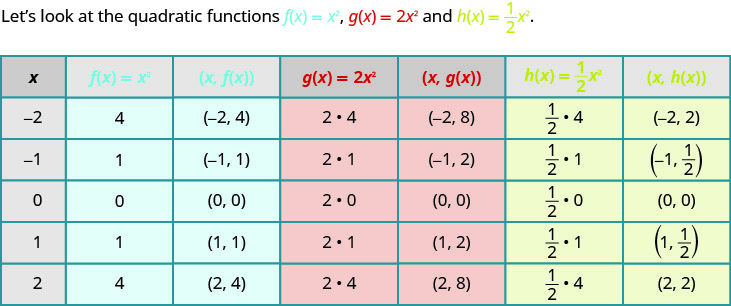
假设,如果我们绘制这些函数的图形\(a\),我们可以看到常量的效果\(a>0\)。
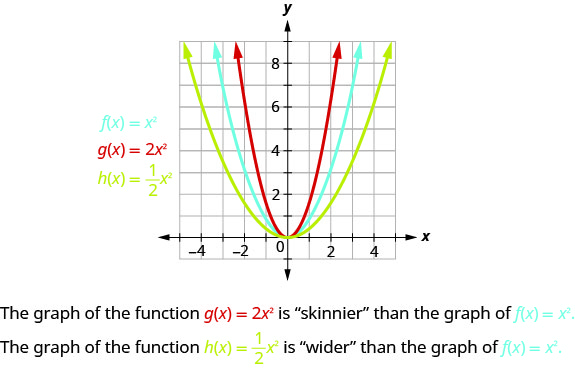
要用常量绘制函数的图形\(a\),最简单的方法是选择几个点\(f(x)=x^{2}\)并将\(y\)-values乘以\(a\)。
形态的二次函数图\(f(x)=ax^{2}\)
函数\(a\)中的系数\(f(x)=x^{2}\)通过拉伸或压缩来\(f(x)=ax^{2}\)影响图形。
- 如果\(0<|a|<1\),的图形\(f(x)=ax^{2}\)将比的图形 “宽”\(f(x)=x^{2}\)。
- 如果\(|a|>1\),的图表\(f(x)=ax^{2}\)将比的图形 “更薄”\(f(x)=x^{2}\)。
图表\(f(x)=3x^{2}\)。
解决方案:
我们将在同一个网格\(g(x)=3x^{2}\)上绘制函数\(f(x)=x^{2}\)和图表。 我们将选择几个点,\(f(x)=x^{2}\)然后将\(y\)-values乘\(3\)以得出分数\(g(x)=3x^{2}\)。
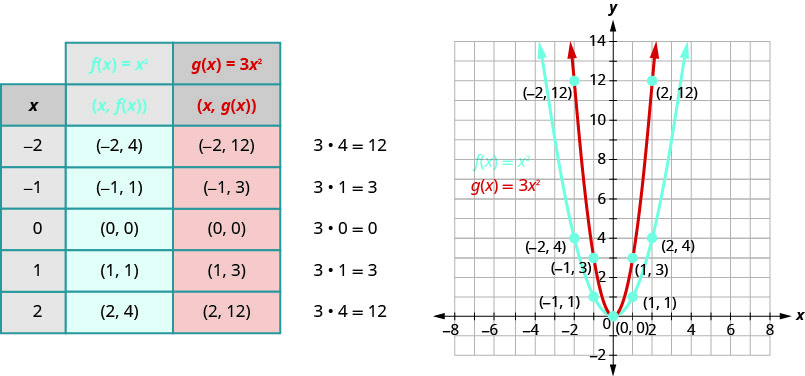
图表\(f(x)=-3x^{2}\)。
- 回答
-
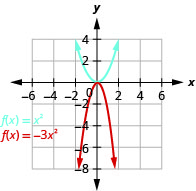
图 9.7.32
图表\(f(x)=2x^{2}\)。
- 回答
-
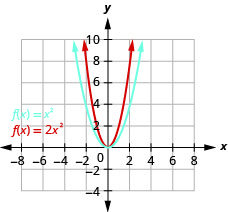
图 9.7.33
使用变换绘制二次函数图
我们已经了解了常量\(a, h\)\(f(x)=x^{2}+k, f(x)=(x−h)^{2}\)、函数\(k\)中的常量和如何\(f(x)=ax^{2}\)影响它们的图形。 现在,我们可以将二次函数放在一起,然后\(f(x)=ax^{2}+bx+c\)通过填写正方形将二次函数放入表单中\(f(x)=a(x−h)^{2}+k\)来绘制二次函数。 这种形式有时被称为顶点形式或标准形式。
我们必须小心谨慎,在函数的同一边加上和减去数字才能完成平方。 我们不能像用二次方程完成正方形时那样将数字相加到两边。

当我们在一个系数不是 1 的函数中完成平方时,我们必须将\(x^{2}\)该系数从\(x\)-terms中分解出来。 我们不将其从常量项中分解出来。 将常量项向右移动一点通常会很有帮助,这样可以更轻松地只关注\(x\)-terms。
一旦我们得到想要完成平方的常数,我们必须记得先将其乘以该系数,然后再将其减去。
通过填写正方形\(f(x)=−3x^{2}−6x−1\)在\(f(x)=a(x−h)^{2}+k\)表单中重写。
解决方案:
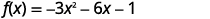 |
|
| 将\(x\)项与常量分开。 | 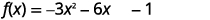 |
| 将系数分解为\(x^{2}, -3\)。 | 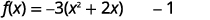 |
| 准备完成方块。 | 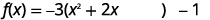 |
| 取一半\(2\)然后将其平整以完成正方形\((\frac{1}{2}\cdot 2)^{2}=1\) | |
| 常量\(1\)补齐圆括号中的正方形,但圆括号乘以\(-3\)。 所以我们真的在补充\(-3\)。 然后,我们必须\(3\)添加而不是更改函数的值。 | 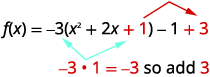 |
| 将三项式重写为正方形并减去常量。 | 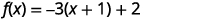 |
| 该函数现在采用表\(f(x)=a(x-h)^{2}+k\)单。 | 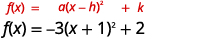 |
通过填写正方形\(f(x)=−4x^{2}−8x+1\)在\(f(x)=a(x−h)^{2}+k\)表单中重写。
- 回答
-
\(f(x)=-4(x+1)^{2}+5\)
通过填写正方形\(f(x)=2x^{2}−8x+3\)在\(f(x)=a(x−h)^{2}+k\)表单中重写。
- 回答
-
\(f(x)=2(x-2)^{2}-5\)
将函数放入\(f(x)=(x−h)^{2}+k\)表单后,我们就可以像在前几个问题中一样使用转换了。 下一个例子将向我们展示如何做到这一点。
使用转换绘\(f(x)=x^{2}+6x+5\)制图表。
解决方案:
步骤 1:通过填写正方形以\(f(x)=a(x-h)^{2}+k\)顶点形式重写函数。
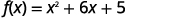 |
|
| 将\(x\)项与常量分开。 | 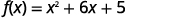 |
| 取一半\(6\)然后将其平整以完成正方形。 \((\frac{1}{2}\cdot 6)^{2}=9\) | |
| 我们\(9\)加减都是\(9\)为了不改变函数的值。 | 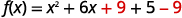 |
| 将三项式重写为正方形并减去常量。 | 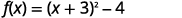 |
| 该函数现在采用表\(f(x)=(x-h)^{2}+k\)单。 | 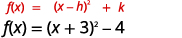 |
第 2 步:使用转换绘制函数图表。
查看这些\(h, k\)值,我们看到图表将取出图形\(f(x)=x^{2}\)并将其向左\(3\)单位和向下\(4\)单位移动。
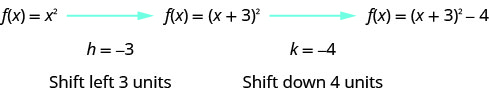
我们首先在网格\(f(x)=x^{2}\)上画出图形。

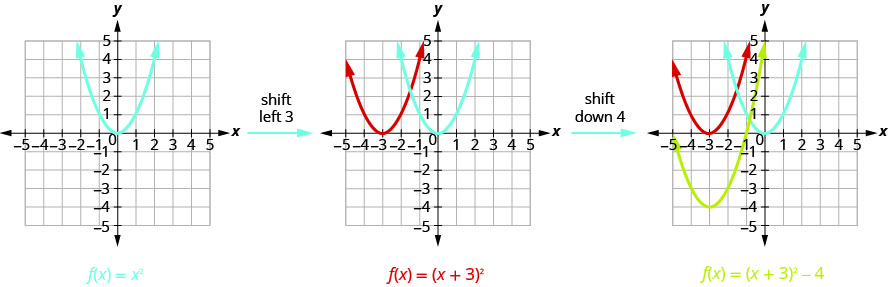
使用转换绘\(f(x)=x^{2}+2x-3\)制图表。
- 回答
-
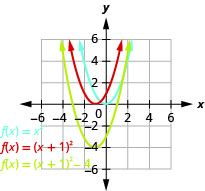
图 9.7.50
使用转换绘\(f(x)=x^{2}-8x+12\)制图表。
- 回答
-
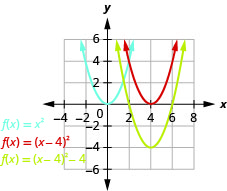
图 9.7.51
我们在此处列出了使用变换绘制二次函数的图形的步骤。
使用变换绘制二次函数的图形
- 通过填写方块来重写\(f(x)=a(x-h)^{2}+k\)表单中的函数。
- 使用转换绘制函数图表。
使用转换绘\(f(x)=-2x^{2}-4x+2\)制图表。
解决方案:
步骤 1:通过填写正方形以\(f(x)=a(x-h)^{2}+k\)顶点形式重写函数。
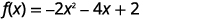 |
|
| 将\(x\)项与常量分开。 | 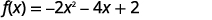 |
| 我们需要将的系数\(x^{2}\)设为一。 我们\(-2\)从\(x\)-terms中考虑因素。 | 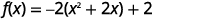 |
| 取一半\(2\)然后将其平整以完成正方形。 \((\frac{1}{2}\cdot 2)^{2}=1\) | |
| 我们在圆括号中加上方形\(1\)以完成方块,但圆括号乘以\(-2\)。 所以我们真的在补充\(-2\)。 为了不更改我们添加的函数的值\(2\)。 | 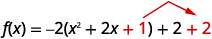 |
| 将三项式重写为正方形并减去常量。 | 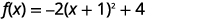 |
| 该函数现在采用表\(f(x)=a(x-h)^{2}+k\)单。 | 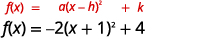 |
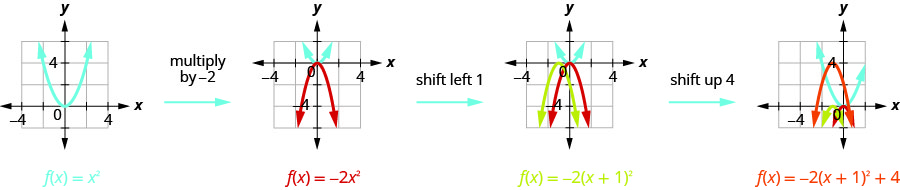
第 2 步:使用转换绘制函数图表。
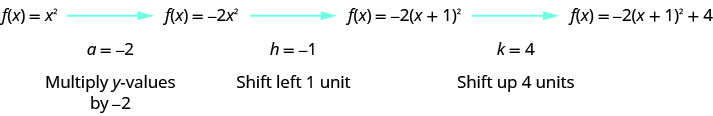
我们首先在网格\(f(x)=x^{2}\)上画出图形。

使用转换绘\(f(x)=-3x^{2}+12x-4\)制图表。
- 回答
-
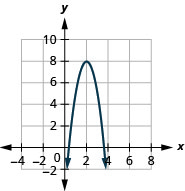
图 9.7.61
使用转换绘\(f(x)=−2x^{2}+12x−9\)制图表。
- 回答
-
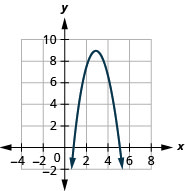
图 9.7.62
现在我们已经完成了方形以\(f(x)=a(x−h)^{2}+k\)形成二次函数,我们也可以像上一节一样使用这种技术使用函数的属性绘制函数的图形。
如果我们回头看最后几个例子,就会发现顶点与常量\(h\)和有关\(k\)。
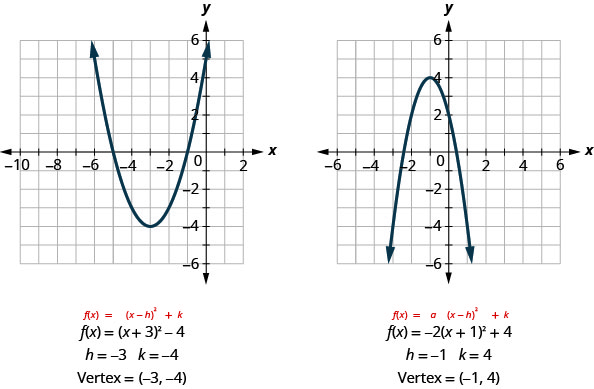
在每种情况下,顶点都是\((h,k)\)。 对称轴也是直线\(x=h\)。
我们重写了使用函数处于\(f(x)=a(x−h)^{2}+k\)形式状态的属性绘制二次函数的步骤。
\(f(x)=a(x-h)^{2}+k\)使用属性绘制表单中的二次函数
- 重写函数表\(f(x)=a(x-h)^{2}+k\)单。
- 确定抛物线是向上打开\(a>0\),还是向下打开\(a<0\)。
- 找到对称轴,\(x=h\)。
- 找到顶点,\((h,k\)。
- 找到\(y\)截距。 在对称轴上找到\(y\)与-截距对称的点。
- 找到\(x\)-截图。
- 绘制抛物线图。
- \(f(x)=2 x^{2}+4 x+5\)在\(f(x)=a(x-h)^{2}+k\)表单中重写
- 使用属性绘制函数图表
解决方案:
| 通过填写方块来重写\(f(x)=a(x-h)^{2}+k\)表单中的函数。 | \(f(x)=2 x^{2}+4 x+5\) |
| \(f(x)=2\left(x^{2}+2 x\right)+5\) | |
| \(f(x)=2\left(x^{2}+2 x+1\right)+5-2\) | |
| \(f(x)=2(x+1)^{2}+3\) | |
| 识别常量\(a, h, k\)。 | \(a=2 h=-1 k=3\) |
| 因为\(a=2\),抛物线向上打开。 |  |
| 对称轴是\(x=h\)。 | 对称轴是\(x=-1\)。 |
| 顶点是\((h,k)\)。 | 顶点是\((-1,3)\)。 |
| 通过查找找到\(y\)-截距\(f(0)\)。 | \(f(0)=2 \cdot 0^{2}+4 \cdot 0+5\) |
| \(f(0)=5\) | |
| \(y\)-截距\((0,5)\) | |
| 找到与对称轴\((0,5)\)对称的点。 | \((-2,5)\) |
| 找到\(x\)-截图。 | 判别值为负,因此没有\(x\)-intercepts。 绘制抛物线图。 |
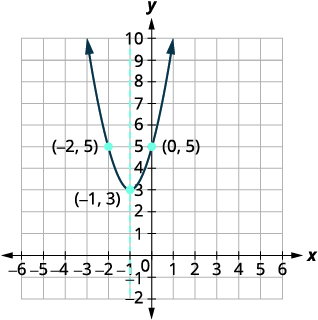 |
- \(f(x)=3 x^{2}-6 x+5\)在\(f(x)=a(x-h)^{2}+k\)表单中重写
- 使用属性绘制函数图表
- 回答
-
- \(f(x)=3(x-1)^{2}+2\)
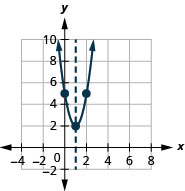
图 9.7.66
- \(f(x)=-2 x^{2}+8 x-7\)在\(f(x)=a(x-h)^{2}+k\)表单中重写
- 使用属性绘制函数图表
- 回答
-
- \(f(x)=-2(x-2)^{2}+1\)
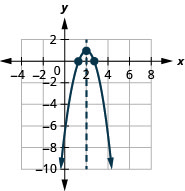
图 9.7.67
从其图形中找到二次函数
到目前为止,我们已经从一个函数开始,然后找到了它的图表。
现在我们要扭转这个过程。 从图表开始,我们将找到函数。
确定显示其图形的二次函数。
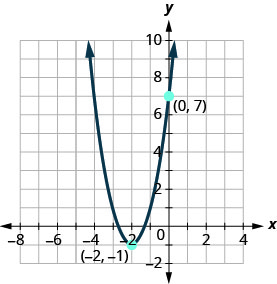
解决方案:
由于它是二次的,所以我们从\(f(x)=a(x−h)^{2}+k\)形式开始。
顶点是\((h,k)\) s\((−2,−1)\) o an\(h=−2\) d\(k=−1\)。
\(f(x)=a(x-(-2))^{2}-1\)
要查找\(a\),我们使用\(y\)-intercept,\((0,7)\)。
所以\(f(0)=7\)。
\(7=a(0+2)^{2}-1\)
求解\(a\)。
\(\begin{array}{l}{7=4 a-1} \\ {8=4 a} \\ {2=a}\end{array}\)
编写函数。
\(f(x)=a(x-h)^{2}+k\)
在\(h=-2, k=-1\)和中替换\(a=2\)。
\(f(x)=2(x+2)^{2}-1\)
以显示图形的\(f(x)=a(x−h)^{2}+k\)形式写下二次函数。
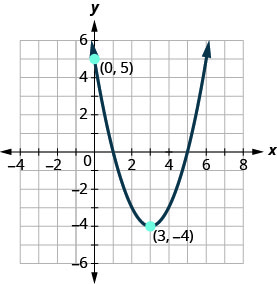
- 回答
-
\(f(x)=(x-3)^{2}-4\)
确定显示其图形的二次函数。
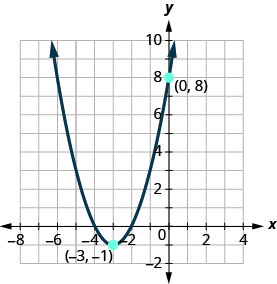
- 回答
-
\(f(x)=(x+3)^{2}-1\)
访问这些在线资源,获取更多指导和练习,使用变换绘制二次函数。
关键概念
- \(f(x)=x^{2}+k\)使用垂直移位绘制形状的二次函数
- 的图表会\(f(x)=x^{2}+k\)移动\(f(x)=x^{2}\)垂直\(k\)单位的图形。
- 如果是\(k>0\),则将抛物线垂直向上移动\(k\)单位。
- 如果为\(k<0\),则将抛物线垂直向下移动\(|k|\)单位。
- 的图表会\(f(x)=x^{2}+k\)移动\(f(x)=x^{2}\)垂直\(k\)单位的图形。
- \(f(x)=(x−h)^{2}\)使用水平偏移绘制形状的二次函数
- 的图表会\(f(x)=(x−h)^{2}\)移动\(f(x)=x^{2}\)水平\(h\)单位的图形。
- 如果是\(h>0\),则将抛物线水平向左移动\(h\)单位。
- 如果是\(h<0\),则将抛物线水平向右移动\(|h|\)单位。
- 的图表会\(f(x)=(x−h)^{2}\)移动\(f(x)=x^{2}\)水平\(h\)单位的图形。
- 形式为二次函数的图形\(f(x)=ax^{2}\)
- 函数\(a\)中的系数\(f(x)=x^{2}\)通过拉伸或压缩来\(f(x)=ax^{2}\)影响图形。
如果\(0<|a|<1\),则的图形\(f(x)=ax^{2}\)将比的图形 “宽”\(f(x)=x^{2}\)。
如果\(|a|>1\),则的图表\(f(x)=ax^{2}\)将比的图形 “更薄”\(f(x)=x^{2}\)。
- 函数\(a\)中的系数\(f(x)=x^{2}\)通过拉伸或压缩来\(f(x)=ax^{2}\)影响图形。
- 如何使用变换绘制二次函数的图形
- 通过填写方块来重写\(f(x)=a(x−h)^{2}+k\)表单中的函数。
- 使用转换绘制函数图表。
- \(f(x)=a(x−h)^{2}+k\)使用属性以顶点形式绘制二次函数的图形
- 以\(f(x)=a(x−h)^{2}+k\)表单重写函数。
- 确定抛物线是向上打开\(a>0\),还是向下打开\(a<0\)。
- 找到对称轴,\(x=h\)。
- 找到顶点,\((h,k)\)。
- 找到\(y\)截距。 在对称轴上找到\(y\)与-截距对称的点。
- 如果可能的话,找到\(x\)-intercepts。
- 绘制抛物线图。


