9.7E：使用属性绘制二次函数图（练习）

Last updated
Save as PDF

Page ID: 204165

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

练习成就完美

练习 1-4：识别二次函数的图

在以下练习中，通过绘制点来绘制函数图表。

1。 $f(x)=x^{2}+3$

2。 $f(x)=x^{2}-3$

3。 $y=-x^{2}+1$

4。 $f(x)=-x^{2}-1$

回答

1。

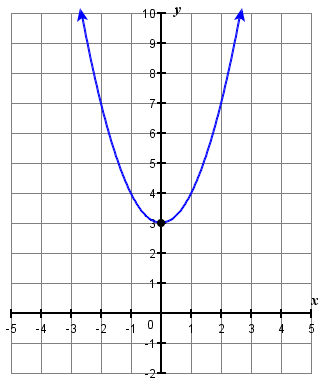
$clipboard_eb78a0f78325e7c8a9cceea709788ca1d.png$

3。

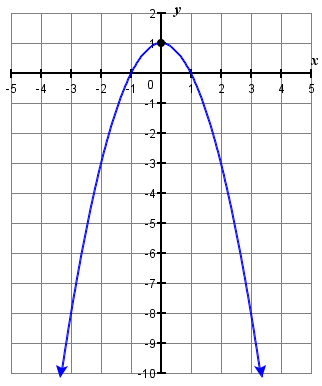
$clipboard_ef318ed788d73edacb2b69f9a778e9ce9.png$

练习 5-8：识别二次函数的图

在以下每个练习中，确定抛物线是向上还是向下打开。

5. a.$f(x)=-2 x^{2}-6 x-7$ b.$f(x)=6 x^{2}+2 x+3$

6. a.$f(x)=4 x^{2}+x-4$ b.$f(x)=-9 x^{2}-24 x-16$

7. a.$f(x)=-3 x^{2}+5 x-1$ b.$f(x)=2 x^{2}-4 x+5$

8. a.$f(x)=x^{2}+3 x-4$ b.$f(x)=-4 x^{2}-12 x-9$

回答

5. a. 向下 b. 向上

7. a. 向下 b. 向上

练习 9-12：找到对称轴和抛物线的顶点

在以下函数中，找到

对称轴方程
其图表的顶点

9。 $f(x)=x^{2}+8 x-1$

10。 $f(x)=x^{2}+10 x+25$

11。 $f(x)=-x^{2}+2 x+5$

12。 $f(x)=-2 x^{2}-8 x-3$

回答

9. a. 对称轴：$x=-4$b。顶点：$(-4,-17)$

11. a. 对称轴：$x=1$b。顶点：$(1,2)$

练习 13-24：找到抛物线的截取物

在以下练习中，找到给定函数的抛物线的截距。

13。 $f(x)=x^{2}+7 x+6$

14。 $f(x)=x^{2}+10 x-11$

15。 $f(x)=x^{2}+8 x+12$

16。 $f(x)=x^{2}+5 x+6$

17。 $f(x)=-x^{2}+8 x-19$

18。 $f(x)=-3 x^{2}+x-1$

19。 $f(x)=x^{2}+6 x+13$

20。 $f(x)=x^{2}+8 x+12$

21。 $f(x)=4 x^{2}-20 x+25$

22。 $f(x)=-x^{2}-14 x-49$

23。 $f(x)=-x^{2}-6 x-9$

24。 $f(x)=4 x^{2}+4 x+1$

回答

13。 $y$-截距:$(0,6)$;$x$-截距:$(-1,0), (-6,0)$

15。 $y$-截距:$(0,12)$;$x$-截距:$(-2,0), (-6,0)$

17。 $y$-截距:$(0,-19)$;$x$-截距:无

19。 $y$-截距:$(0,13)$;$x$-截距:无

21。 $y$-截距:$(0,-16)$;$x$-截距:$(\frac{5}{2},0)$

23。 $y$-截距:$(0,9)$;$x$-截距:$(-3,0)$

练习 25-42：使用属性绘制二次函数图

在以下练习中，使用函数的属性绘制函数的图表。

25。 $f(x)=x^{2}+6 x+5$

26。 $f(x)=x^{2}+4 x-12$

27。 $f(x)=x^{2}+4 x+3$

28。 $f(x)=x^{2}-6 x+8$

29。 $f(x)=9 x^{2}+12 x+4$

30。 $f(x)=-x^{2}+8 x-16$

31。 $f(x)=-x^{2}+2 x-7$

32。 $f(x)=5 x^{2}+2$

33。 $f(x)=2 x^{2}-4 x+1$

34。 $f(x)=3 x^{2}-6 x-1$

35。 $f(x)=2 x^{2}-4 x+2$

36。 $f(x)=-4 x^{2}-6 x-2$

37。 $f(x)=-x^{2}-4 x+2$

38。 $f(x)=x^{2}+6 x+8$

39。 $f(x)=5 x^{2}-10 x+8$

40。 $f(x)=-16 x^{2}+24 x-9$

41。 $f(x)=3 x^{2}+18 x+20$

42。 $f(x)=-2 x^{2}+8 x-10$

回答

25。

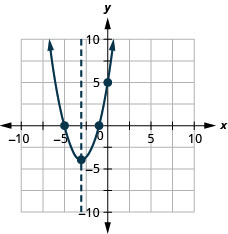
此图显示了在 x y 坐标平面上绘制的向上开口的抛物线。飞机的 x 轴从负 10 延伸到 10。飞机的 y 轴从负 10 延伸到 10。抛物线的顶点位于（负 3，负 4）。绘制 y 截距，即点 (0, 5)，以及 x 截距（负 5, 0）和（负 1, 0）。 — 图 9.6.136

27。

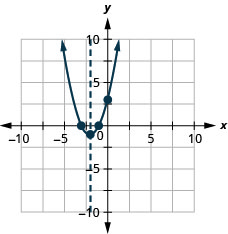
此图显示了在 x y 坐标平面上绘制的向上开口的抛物线。飞机的 x 轴从负 10 延伸到 10。飞机的 y 轴从负 10 延伸到 10。抛物线的顶点位于（负 2，负 1）。绘制 y 截距，即点 (0, 3)，以及 x 截距（负 3, 0）和（负 1, 0）。 — 图 9.6.137

29。

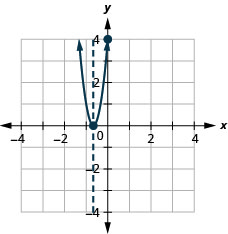
此图显示了在 x y 坐标平面上绘制的向上开口的抛物线。飞机的 x 轴从负 4 延伸到 4。飞机的 y 轴从负 4 延伸到 4。抛物线的顶点位于（负三分之二，0）。绘制了 y 截距，即点 (0, 4)。对称轴 x 等于负三分之二，绘制为垂直虚线。 — 图 9.6.138

31。

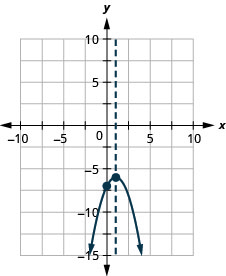
此图显示了在 x y 坐标平面上绘制的向下开口的抛物线。飞机的 x 轴从负 10 延伸到 10。飞机的 y 轴从负 15 延伸到 10。抛物线的顶点位于 (1，负 6)。绘制了 y 截距，即点 (0，负 7)。对称轴 x 等于 1，绘制为一条垂直虚线。 — 图 9.6.139

33。

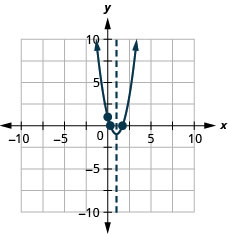
此图显示了在 x y 坐标平面上绘制的向上开口的抛物线。飞机的 x 轴从负 10 延伸到 10。飞机的 y 轴从负 10 延伸到 10。抛物线的顶点位于 (1，负 1)。 y 截距点 (0, 1) 与 x 截距一样绘制，大约为 (0.3, 0) 和 (1.7, 0)。对称轴是垂直线 x 等于 1，绘制为虚线。 — 图 9.6.140

35。

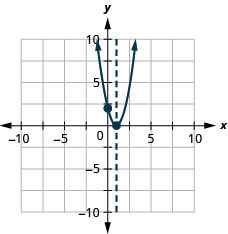
此图显示了在 x y 坐标平面上绘制的向上开口的抛物线。飞机的 x 轴从负 10 延伸到 10。飞机的 y 轴从负 10 延伸到 10。抛物线在 (1, 0) 处有一个顶点。这个点是唯一的 x 截距。绘制了 y 截距，即点 (0, 2)。对称轴是垂直线 x 等于 1，绘制为虚线。 — 图 9.6.141

37。

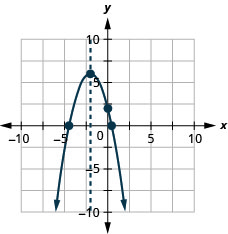
此图显示了在 x y 坐标平面上绘制的向下开口的抛物线。飞机的 x 轴从负 10 延伸到 10。飞机的 y 轴从负 10 延伸到 10。抛物线的顶点位于（负 2, 6）。 y 截距点 (0, 2) 与 x 截距一样绘制，大致为（负 4.4、0）和（0.4、0）。对称轴是垂直线 x 等于 2，绘制为虚线。 — 图 9.6.142

39。

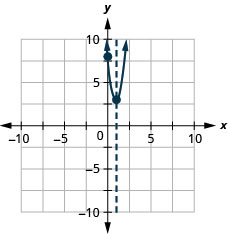
此图显示了在 x y 坐标平面上绘制的向上开口的抛物线。飞机的 x 轴从负 10 延伸到 10。飞机的 y 轴从负 10 延伸到 10。抛物线在 (1, 3) 处有一个顶点。绘制了 y 截距，即点 (0, 8)；没有 x 截距。对称轴是垂直线 x 等于 1，绘制为虚线。 — 图 9.6.143

41。

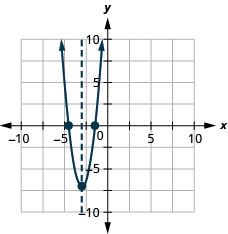
此图显示了在 x y 坐标平面上绘制的向上开口的抛物线。飞机的 x 轴从负 10 延伸到 10。飞机的 y 轴从负 10 延伸到 10。抛物线的顶点位于（负 3，负 7）。 X 截距绘制在近似点（负 4.5、0）和（负 1.5、0）处。对称轴是垂直线 x 等于负 3，绘制为虚线。 — 图 9.6.144

练习 43-48：求解最大值和最小值应用程序

在以下练习中，找到每个函数的最大值或最小值。

43。 $f(x)=2 x^{2}+x-1$

44。 $y=-4 x^{2}+12 x-5$

45。 $y=x^{2}-6 x+15$

46。 $y=-x^{2}+4 x-5$

47。 $y=-9 x^{2}+16$

48。 $y=4 x^{2}-49$

回答

43。最小值为 w$−\frac{9}{8}$ hen$x=−\frac{1}{4}$。

45。最大值为 wh$6$ en$x=3$。

47。最大值为 wh$16$ en$x=0$。

练习 49-60：求解最大值和最小值应用程序

在以下练习中，求解。将答案四舍五入到最接近的十分之一。

49。一支箭以英尺$168$ /秒的速度从平台$45$英尺高处垂直向上射出。使用二次函数$h(t)=-16 t^{2}+168 t+45$找出箭头达到其最大高度需要多长时间，然后找到最大高度。

50。一块石头从高度为$20$英尺的平台垂直向上投掷，速度为英$160$尺/秒。使用二次函数找$h(t)=-16 t^{2}+160 t+20$出宝石达到其最大高度需要多长时间，然后找到最大高度。

51。球从地面垂直向上投掷，初始速度为$109$ ft/sec。使用二次函数$h(t)=-16 t^{2}+109 t+0$找出球达到最大高度需要多长时间，然后找到最大高度。

52。球从地面垂直向上投掷，初始速度为$122$ ft/sec。使用二次函数$h(t)=-16 t^{2}+122 t+0$找出球达到最大高度需要多长时间，然后找到最大高度。

53。一家计算机商店老板估计，通过为某台计算机每人收取$x$美元，他可以每周出售$40 − x$计算机。二次函数$R(x)=-x^{2}+40 x$用于查找计算机的销售价格为时获得的收入$R$$x$，找到能给他带来最大收入的卖出价格，然后找出最大收入的金额。

54。一家销售背包的零售商估计，通过以每包$x$美元的价格出售$100 − x$背包，他将能够每月销售背包。二次函数$R(x)=-x^{2}+100 x$用于查找在$R$背包的售价为时收到的$x$。找到能给他带来最大收入的销售价格，然后找到最高收入的金额。

55。一家销售时装靴的零售商估计，通过以每双$x$美元的价格出售，他将能够每周销售$70 − x$靴子。使用二次函数$R(x)=-x^{2}+70 x$查找当一双时尚靴的平均售价为时获得的收入$x$。找到能给他带来最大收入的销售价格，然后找到每天最高收入的金额。

56。一家手机公司估计，通过为某部手机每人收取$x$美元，他们每天可以出售$8 − x$手机。使用二次函数$R(x)=-x^{2}+8 x$查找当手机的售价为时每天获得的收入$x$。找到能为他们带来每日最大收入的销售价格，然后找到最高收入的金额。

57。牧场主要在河边围栏的三面围栏。他需要使用几$240$英尺的围栏来最大限度地扩大畜栏面积。二次方程$A(x)=x(240-2 x)$给出了畜栏的面积$A$，即沿河畜栏的长度。$x$ 找到沿河畜栏的长度，该长度将给出最大面积，然后找到畜栏的最大面积。

58。一位兽医正在他的建筑物旁边封闭一个矩形的户外跑步区，供他照顾的狗使用。他需要使用$100$英尺的围栏来最大限度地扩大面积。二次函数$A(x)=x(100-2 x)$给出了与狗跑接壤的建筑物的长度所占的面积。$A$$x$ 找出应与狗跑接壤的建筑物的长度以给出最大面积，然后找到狗跑的最大面积。

59。一位土地所有者正计划在自己的车库后面建造一个围栏的矩形露台，将自己的车库作为 “墙” 之一。他想用$80$英尺的围栏最大限度地扩大面积。二次函数$A(x)=x(80-2 x)$给出了露台的面积，其中$x$是一侧的宽度。找到露台的最大面积。

60。一家有三个年幼的孩子刚搬进一所院子里没有围栏的房子。以前的主人给了他们一$300$英尺的围栏，用来封闭部分后院。使用二次函数$A(x)=x(300-2 x)$来确定围栏的最大面积（以码为单位）。

回答

49。在几$5.3$秒钟内，箭头将达到$486$英尺的最大高度。

51。在$3.4$几秒钟内，球将达到其最大$185.6$英尺高度。

53。 $20$计算机将在收据$400$中提供的最大金额为美元。

55。他将能够以最高收入出售$35$两双靴子 $$1,225$.

57。畜栏河边的长度为$120$英尺，最大面积为$7,200$平方英尺。

59。露台的最大面积为$800$英尺.

练习 61-64：写作练习

61。函数图$f(x)=x^{2}$和图表$f(x)=x^{2}−1$有何不同？我们在本节开头绘制了它们的图表。他们的图表有什么区别？他们的图表怎么样？

62。解释寻找抛物线顶点的过程。

63。解释如何找到抛物线的截取点。

64。在绘制二次函数时如何使用判别函数？

回答

1。答案会有所不同。

3。答案会有所不同。

自检

a. 完成练习后，使用此清单评估您对本节目标的掌握程度。

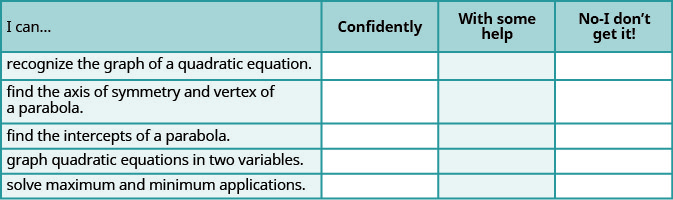
此表提供了一份清单，用于评估对本节目标的掌握程度。选择你将如何回应 “我能识别二次方程的图表” 的说法。“自信地，” 在一些帮助下，“或” 不，我不明白。” 选择你将如何回应这句话 “我能找到抛物线的对称轴和顶点。” ¿€with™帮点忙，“或者 “不，我不明白。” 选择你将如何回应这句话 “我能找到抛物线的拦截。” 自信地，“在一些帮助下，” 或 “不，我不明白。两个变量中的 ratic 方程。™™“自信地，” 有了一些帮助，” 或 “不，我不明白。”™ 选择你将如何回应这份声明 “我能解决最大和最少的申请。”™ — 图 9.6.145