9.7：使用属性绘制二次函数图

Last updated
Save as PDF

Page ID: 204150

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

学习目标

在本节结束时，您将能够：

识别二次函数的图形
找到对称轴和抛物线的顶点
找出抛物线的截距
使用属性绘制二次函数的图形
求解最大值和最小值应用程序

在开始之前，请参加这个准备测验。

$f(x)=x^{2}$通过绘制点来绘制函数图表。
如果你错过了这个问题，请查看示例 3.54。
解决：$2 x^{2}+3 x-2=0$。
如果您错过了此问题，请查看示例 6.45。
评估$-\frac{b}{2 a}$何时$a=3$和$b=-6$。
如果你错过了这个问题，请查看示例 1.21。

识别二次函数的图形

之前我们非常简要地看过这个函数$f(x)=x^{2}$，我们称之为方函数。它是我们研究的第一批非线性函数之一。现在我们将绘制形式$f(x)=a x^{2}+b x+c$为 if 的函数$a \neq 0$。我们将这种函数称为二次函数。

定义$\PageIndex{1}$

二次函数，其中$a, b$，和$c$是实数$a≠0$，是以下形式的函数

$f(x)=a x^{2}+b x+c$

我们通过绘制点$f(x)=x^{2}$来绘制二次函数的图形。

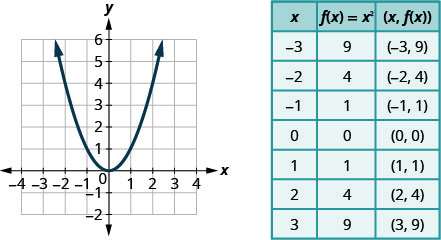
此图显示了在 x y 坐标平面上绘制的向上开口的抛物线。飞机的 x 轴从负 4 延伸到 4。飞机的 y 轴从负 2 延伸到 6。抛物线在 (0, 0) 处有一个顶点，还要穿过点 (-2、4)、(-1、1)、(2、4)。图表右侧是一个包含 3 列的值表。第一行是标题行，标注每列，“x”，“f of x” 等于 x squaredα€，“订单对 x，f of x”。在第 2 行中，x 等于负 3，x 的 f 等于 x 平方为 9，有序对 x、f of x 是负数 3、9。在第 3 行中，x 等于负 2，x 的 f 等于 x 平方为 4，有序对 x, f of x 是有序对负 2, 4。在第 4 行中，x 等于负 1，x 的 f 等于 x 平方为 1，有序对 x, f of x 是有序对负 1, 1。在第 5 行中，x 等于 0，x 的 f 等于 x 平方为 0，有序对 x, f of x 是有序对 0, 0。在第 6 行中，x 等于 1，x 的 f 等于 x 平方为 1，有序对 x，f of x 是有序对 1、1。在第 7 行中，x 等于 2，x 的 f 等于 x 的平方为 4，有序对 x，f of x 是有序对 2、4。在第 8 行中，x 等于 3，x 的 f 等于 x 平方为 9，有序对 x，f of x 是有序对 3、9。 — 图 9.6.1

每个二次函数都有一个看起来像这样的图形。我们称这个数字为抛物线。让我们练习通过绘制几个点来绘制抛物线。

示例$\PageIndex{1}$

图表：$f(x)=x^{2}-1$。

解决方案：

我们将通过绘制点来绘制函数的图形。

选择整数值$x$，将它们替换到方程中，然后简化即可查找$f(x)$。在图表中记录有序货币对的值。	$。$
绘制这些点，然后用平滑曲线将它们连接起来。结果将是函数的图形$f(x)=x^{2}-1$。	$。$

练习$\PageIndex{1}$

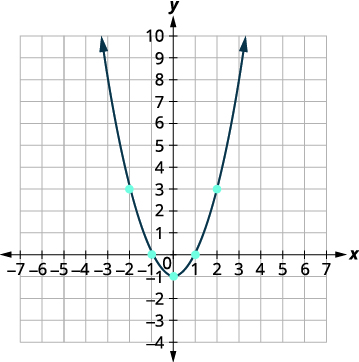图表$f(x)=-x^{2}$。

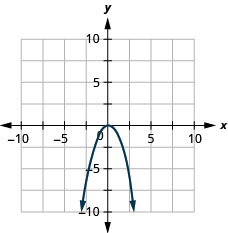
回答: $此图显示了在 x y 坐标平面上绘制的向下开口的抛物线。飞机的 x 轴从负 10 延伸到 10。飞机的 y 轴从负 10 延伸到 10。抛物线在 (0, 0) 处有一个顶点。$

练习$\PageIndex{2}$

图表$f(x)=x^{2}-1$。

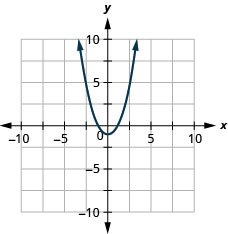
回答: $此图显示了在 x y 坐标平面上绘制的向上开口的抛物线。飞机的 x 轴从负 10 延伸到 10。飞机的 y 轴从负 10 延伸到 10。抛物线在 (0, '1) 处有一个顶点。$

该形式的所有二次函数图$f(x)=a x^{2}+b x+c$都是向上或向下打开的抛物线。参见图 9.6.6

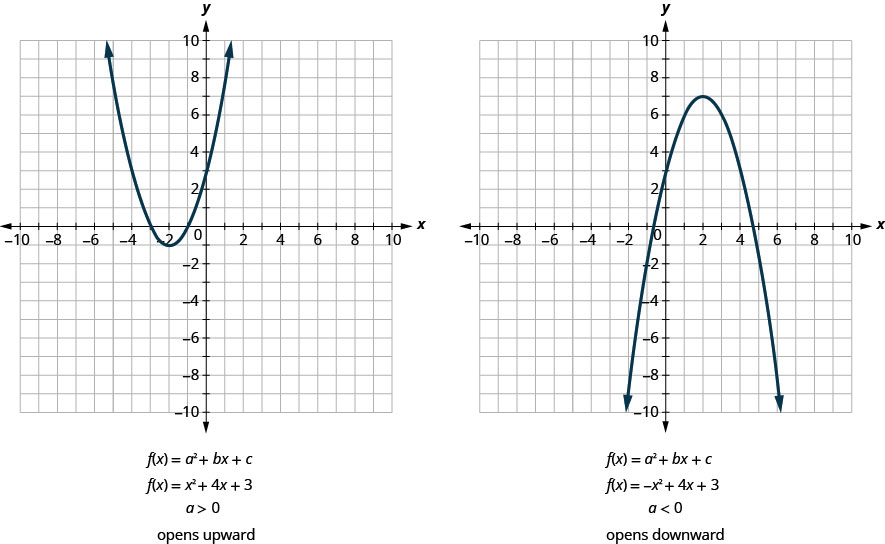
此图并排显示了 2 张图表。左边的图表显示了在 x y 坐标平面上绘制的向上开口的抛物线。飞机的 x 轴从负 10 延伸到 10。飞机的 y 轴从负 10 延伸到 10。抛物线的顶点位于（负 2，负 1），并穿过点（负 4、3）和（0、3）。该图方程的一般形式为 f of x 等于 a x 平方加 b x 加 c。这个抛物线的方程为 x 平方加 4 x 加 3。前导系数 a 大于 0，因此该抛物线向上打开。右图显示了在 x y 坐标平面上绘制的向下开口的抛物线。飞机的 x 轴从负 10 延伸到 10。飞机的 y 轴从负 10 延伸到 10。抛物线在 (2, 7) 处有一个顶点并穿过点 (0, 3) 和 (4, 3)。该图方程的一般形式为 f of x 等于 a x 平方加 b x 加 c。这个抛物线的方程为负 x 平方加 4 x 加 3。前导系数 a 小于 0，因此该抛物线向下打开。

请注意，这两个函数的唯一区别是二次项前的负号（$x^{2}$在图 9.6.6 中的图形方程中）。当二次项为正时，抛物线向上打开；当二次项为负时，抛物线向下打开。

定义$\PageIndex{2}$

抛物线方向

对于二次函数的图形$f(x)=a x^{2}+b x+c$，如果

$此图像显示了项目符号列表。第一个项目符号指出，如果 a 大于 0，则抛物线向上打开并显示向上打开的抛物线的图像。第二个项目符号指出，如果 a 小于 0，则抛物线向下打开并显示向下打开的抛物线的图像。$

示例$\PageIndex{2}$

确定每个抛物线是向上还是向下打开：

$f(x)=-3 x^{2}+2 x-4$
$f(x)=6 x^{2}+7 x-9$

解决方案：

a. 找出的值$a$。

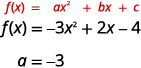
由于$a$是负数，抛物线将向下开放。

b. 找出的值$a$。

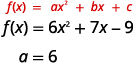
由于$a$为正，抛物线将向上开放。

练习$\PageIndex{3}$

确定每个函数的图形是向上打开还是向下打开的抛物线：

$f(x)=2 x^{2}+5 x-2$
$f(x)=-3 x^{2}-4 x+7$

回答

向上
向下

练习$\PageIndex{4}$

确定每个函数的图形是向上打开还是向下打开的抛物线：

$f(x)=-2 x^{2}-2 x-3$
$f(x)=5 x^{2}-2 x-1$

回答

向下
向上

找到抛物线的对称轴和顶点

再看一下图 9.6.10。你看见我们可以把每个抛物线折成两半然后一面会放在另一面之上吗？ “折叠线” 是一条对称线。我们称之为抛物线的对称轴。

我们用对称轴再次显示相同的两张图。

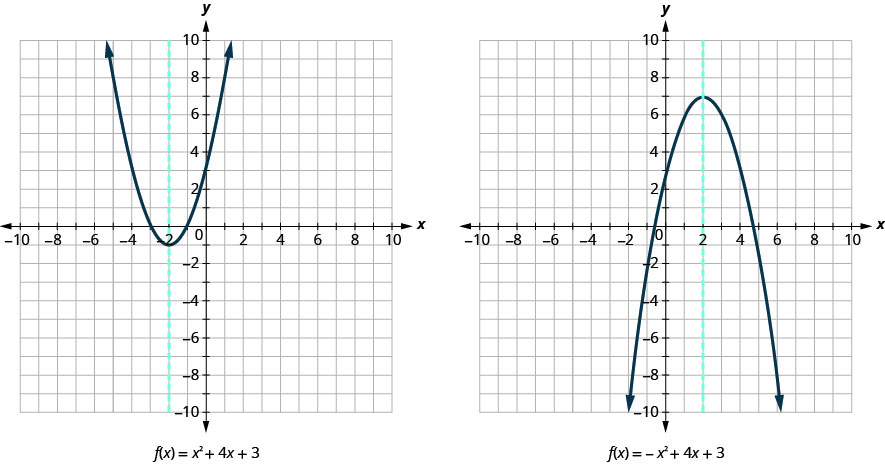
此图并排显示了 2 张图表。左边的图表显示了在 x y 坐标平面上绘制的向上开口的抛物线和一条垂直虚线。飞机的 x 轴从负 10 延伸到 10。飞机的 y 轴从负 10 延伸到 10。抛物线的顶点位于（负 2，负 1），并穿过点（负 4、3）和（0、3）。这个抛物线的方程为 x 平方加 4 x 加 3。垂直线穿过点（负 2, 0），方程 x 等于负 2。右图显示了在 x y 坐标平面上绘制的向下开口的抛物线和一条垂直虚线。飞机的 x 轴从负 10 延伸到 10。飞机的 y 轴从负 10 延伸到 10。抛物线在 (2, 7) 处有一个顶点并穿过点 (0, 3) 和 (4, 3)。这个抛物线的方程为负 x 平方加 4 x 加 3。垂直线穿过点 (2, 0)，方程 x 等于 2。

可以使用二次公式得出对称轴的方程。我们将省略此处的推导并直接使用结果。图形对称轴的方程$f(x)=a x^{2}+b x+c$为$x=-\frac{b}{2 a}$。

因此，为了找到上面绘制的每个抛物线的对称方程，我们将代入公式$x=-\frac{b}{2 a}$。

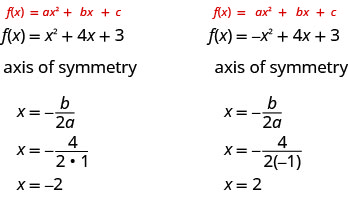
将 x 的函数 f 等于 x 平方加 4 x 加 3 与二次函数的标准形式进行比较，x 的 f 等于 a x 平方加 b x 加 c。对称轴是线 x 等于负 b 除以乘积 2 a。替换 b 和 a 得出 x 等于负 4 除以 2 倍1。对称轴等于负 2。接下来，将 x 的函数 f 等于负 x 平方加 4 x 加 3 与二次函数的标准形式进行比较，x 的 f 等于 a x 平方加 b x 加 c。对称轴是线 x 等于负 b 除以乘积 2 a。用 b 和 a 代替 x 等于负 4 除以产品 2 倍负值 1。对称轴等于 2。

请注意，这些是图表上蓝色虚线的方程式。

抛物线上最低（抛物线向上打开）或最高点（抛物线向下打开）的点位于对称轴上。这个点被称为抛物线的顶点。

我们可以很容易地找到顶点的坐标，因为我们知道它位于对称轴上。这意味着它的
$x$-坐标是$-\frac{b}{2 a}$。为了找到顶点的$y$坐标，我们将$x$-坐标的值替换为二次函数。

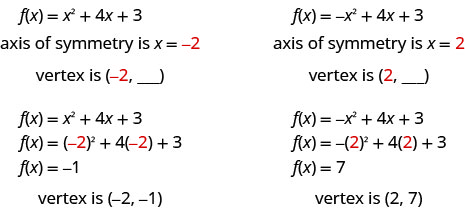
对于 x 的函数 f 等于 x 平方加 4 x 加 3，对称轴为 x 等于负 2。顶点是抛物线上的点，x 坐标为负 2。将 x 等于负 2 替换为函数 f of x 等于 x 平方加 4 x 加 3。 x 的 F 等于负 2 的平方加 4 乘以负 2 加 3，所以 x 的 f 等于负 1。顶点是点（负 2，负 1）。对于 x 的函数 f 等于负 x 平方加 4 x 加 3，则对称轴为 x 等于 2。顶点是抛物线上的 x 坐标为 2 的点。将 x 等于 2 替换为函数 f of x 等于 x 平方加 4 x 加 3。 x 的 F 等于 2 平方加 4 乘以 2 加 3，所以 x 的 f 等于 7。顶点是点 (2, 7)。

抛物线的对称轴和顶点

该函数的图形$f(x)=a x^{2}+b x+c$是一个抛物线，其中：

对称轴是垂直线$x=-\frac{b}{2 a}$。
顶点是对称轴上的一个点，所以它的$x$-坐标是$-\frac{b}{2 a}$
顶点$y$的坐标是通过代$x=-\frac{b}{2 a}$入二次方程来找到的。

示例$\PageIndex{3}$

对于$f(x)=3 x^{2}-6 x+2$查找图：

对称轴
顶点

解决方案：

一个。

	$。$
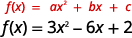对称轴是垂直线$x=-\frac{b}{2 a}$。
将这些值替换$a,b$到方程中。	$x=-\frac{-6}{2 \cdot 3}$
简化。	$x=1$
	对称轴是直线$x=1$。

b。

	$f(x)=3 x^{2}-6 x+2$
顶点是对称线上的一个点，所以它的$x$-坐标将是$x=1$。查找$f(1)$。	$。$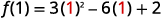
简化。	$。$
结果是$y$-坐标。	$f(1)=-1$
	顶点是$(1,-1)$。

练习$\PageIndex{5}$

对于$f(x)=2 x^{2}-8 x+1$查找图：

对称轴
顶点

回答

$x=2$
$(2,-7)$

练习$\PageIndex{6}$

对于$f(x)=2 x^{2}-4 x-3$查找图：

对称轴
顶点

回答

$x=1$
$(1,-5)$

找出抛物线的截取物

当我们绘制线性方程时，我们经常使用$x$-和$y$-截距来帮助我们绘制线条图。找到拦截的坐标也将有助于我们绘制抛物线图。

请记住，在$y$-intercept 处的值$x$为零。因此，为了找到$y$-intercept，我们$x=0$将其替换为函数。

让我们找出图 9.6.20 所示的两个抛物线的$y$截距。

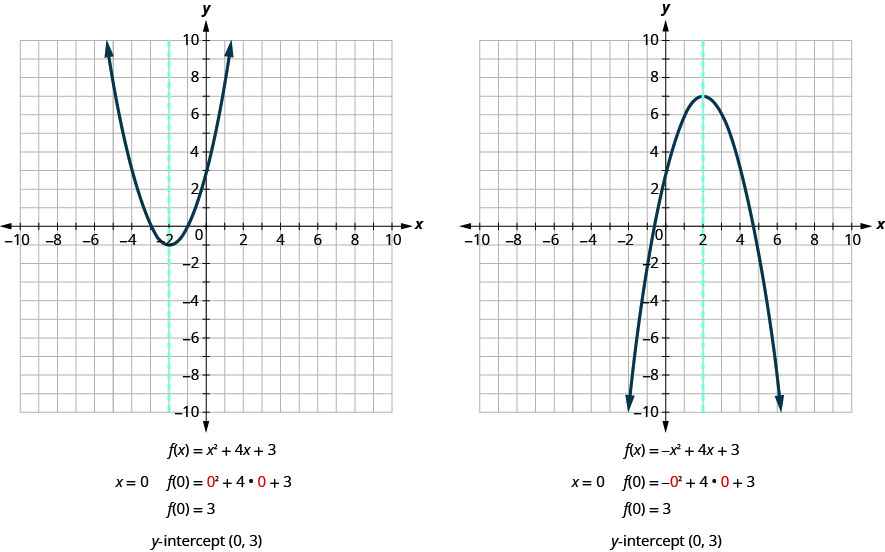
此图并排显示了 2 张图表。左边的图表显示了在 x y 坐标平面上绘制的向上开口的抛物线和一条垂直虚线。飞机的 x 轴从负 10 延伸到 10。飞机的 y 轴从负 10 延伸到 10。抛物线的顶点位于（负 2，负 1），并穿过点（负 4、3）和（0、3）。垂直线是抛物线的对称轴，它穿过该点（负 2, 0）。它的方程式 x 等于负 2。这个抛物线的方程为 x 平方加 4 x 加 3。当 x 等于 0 时，0 的 f 等于 0 的平方加 4 乘以 0 加 3。 0 的 F 等于 3。图形的 y 截距是点 (0, 3)。右图显示了在 x y 坐标平面上绘制的向下开口的抛物线和一条垂直虚线。飞机的 x 轴从负 10 延伸到 10。飞机的 y 轴从负 10 延伸到 10。抛物线在 (2, 7) 处有一个顶点并穿过点 (0, 3) 和 (4, 3)。垂直线是抛物线的对称轴，穿过点 (2, 0)。它的方程式 x 等于 2。这个抛物线的方程为负 x 平方加 4 x 加 3。当 x 等于 0 时，0 的 f 等于负 0 平方加上 4 倍 0 加 3。 0 的 F 等于 3。图形的 y 截距是点 (0, 3)。

当的值为零时，会产生$x$-截距。$f(x)$ 为了找到一个$x$-截距，我们让$f(x)=0$。换句话说，我们需要求解方程式$0=a x^{2}+b x+c$$x$。

$\begin{aligned} f(x) &=a x^{2}+b x+c \\ 0 &=a x^{2}+b x+c \end{aligned}$

像这样求解二次方程正是我们在本章前面所做的！

我们现在可以找到我们看过$x$的两个抛物线的截距了。首先，我们将找到函数为的抛物线的$x$-intercepts$f(x)=x^{2}+4 x+3$。

	$f(x)=x^{2}+4 x+3$
让$f(x)=0$。	$\color{red}0\color{black}=x^{2}+4 x+3$
因子。	$0=(x+1)(x+3)$
使用 “零积分” 属性。	$x+1=0 \quad x+3=0$
解决。	$x=-1 \quad x=-3$
	$x$-intercepts 是$(-1,0)$和$(-3,0)$。

现在我们将找到函数为的抛物线的$x$-intercepts$f(x)=-x^{2}+4 x+3$。

	$f(x)=-x^{2}+4 x+3$
让$f(x)=0$。	$\color{red}0 \color{black}=-x^{2}+4 x+3$
这个二次不分解，所以我们使用二次方程式。	$x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}$
$a=-1, b=4, c=3$	$x=\frac{-4 \pm \sqrt{4^{2}-4(-1)(3)}}{2(-1)}$
简化。	$x=\frac{-4 \pm \sqrt{28}}{-2}$
	$x=\frac{-4 \pm 2 \sqrt{7}}{-2}$
	$x=\frac{-2(2 \pm \sqrt{7})}{-2}$
	$x=2 \pm \sqrt{7}$
	$x$-intercepts 是$(2+\sqrt{7}, 0)$和$(2-\sqrt{7}, 0)$。

我们将使用$x$-intercepts的十进制近似值，这样我们就可以在图表上找到这些点，

$(2+\sqrt{7}, 0) \approx(4.6,0) \quad(2-\sqrt{7}, 0) \approx(-0.6,0)$

这些结果与我们的图表一致吗？参见图 9.6.34

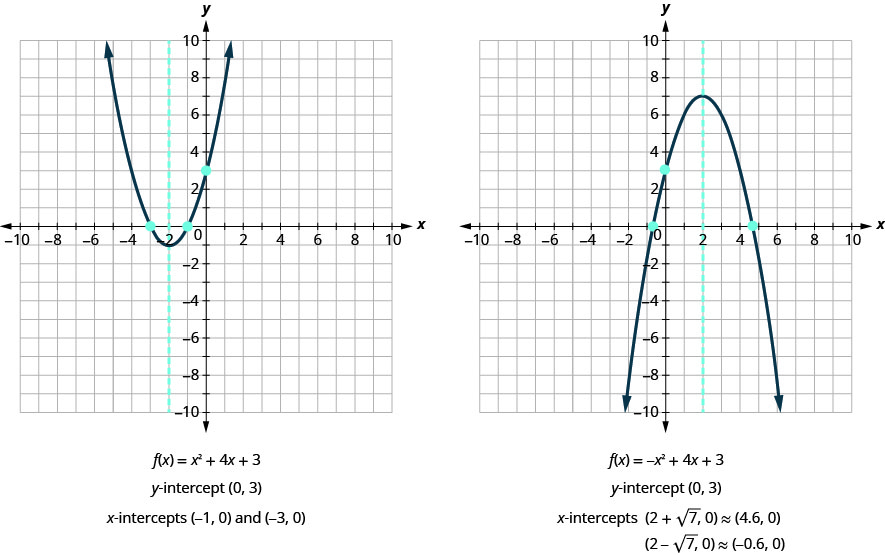
此图并排显示了 2 张图表。左边的图表显示了由函数 f of x 定义的向上开口的抛物线等于 x 平方加 4 x 加 3 和一条垂直虚线 x 等于负 2，在 x y 坐标平面上绘制。飞机的 x 轴从负 10 延伸到 10。飞机的 y 轴从负 10 延伸到 10。抛物线的顶点位于（负 2，负 1）。 y 截距为 (0, 3)，x 截距为（负 1, 0）和（负 3, 0）。右边的图表显示了由 x 的函数 f 定义的向下开口的抛物线等于负 x 平方加 4 x 加 3 和一条在 x y 坐标平面上绘制的垂直虚线 x 等于 2。飞机的 x 轴从负 10 延伸到 10。飞机的 y 轴从负 10 延伸到 10。抛物线在 (2, 7) 处有一个顶点。 y 截距为 (0, 3)，x 截距为（2 加平方根 7、0）、大约（4.6、0）和（2 减去平方根，0），大致为（负 0.6、0）。

找出抛物线的截取物

要找到其功能为的抛物线的截距$f(x)=a x^{2}+b x+c$：

$y$-截距

让我们$x=0$来解决吧$f(x)$。

$x$-拦截

让我们$f(x)=0$来解决吧$x$

示例$\PageIndex{4}$

找出函数为的抛物线的截距$f(x)=x^{2}-2 x-8$。

解决方案：

要找到$y$-截距$x=0$，让我们求解$f(x)$。	$f(x)=x^{2}-2 x-8$
	$f(0)=\color{red}0\color{black}^{2}-2 \cdot \color{red}0 \color{black}-8$
	$f(0)=-8$
	那么$x=0$，什么时候$f(0)=-8$。 $y$-截距是重点$(0,-8)$。
要找到$x$-截距$f(x)=0$，让我们求解$x$。	$f(x)=x^{2}-2 x-8$
	$0=x^{2}-2 x-8$
通过分解求解。	$0=(x-4)(x+2)$
	$0=x-4 \quad 0=x+2$
	$4=x \quad-2=x$
	什么时候$f(x)=0$，然后$x=4$或$x=-2$。 $x$-intercepts 是积分$(4,0)$和$(-2,0)$。

练习$\PageIndex{7}$

找出函数为的抛物线的截距$f(x)=x^{2}+2 x-8$。

回答: $y$-拦截：$(0,-8) x$-拦截$(-4,0),(2,0)$

练习$\PageIndex{8}$

找出函数为的抛物线的截距$f(x)=x^{2}-4 x-12$。

回答: $y$-拦截：$(0,-12) x$-拦截$(-2,0),(6,0)$

在本章中，我们一直在求解这种形式的二次方程$a x^{2}+b x+c=0$。我们求解了$x$，结果就是方程的解。

我们现在正在研究这种形式的二次函数$f(x)=a x^{2}+b x+c$。这些函数的图表是抛物线。 抛物线的截击发生在哪里$f(x)=0$。$x$

例如：

二次方程

$\begin{aligned}x^{2}-2 x-15 & =0\quad \text{Let}\:f(x)=0 \\ (x-5)(x+3) &=0 \\ x-5=0\:\:x+3 & =0 \\ x=5\:\:\:x&=-3\end{aligned}$

二次函数

$\begin{aligned} f(x) &=x^{2}-2 x-15 \\ 0 &=x^{2}-2 x-15 \\ 0 &=(x-5)(x+3) \\ x-5 &=0 \quad x+3=0 \\ x &=5 \quad x=-3 \\(5,0) & \text { and }(-3,0) \\& x\text { -intercepts } \end{aligned}$

二次函数的解是$x$ - 截距的$x$值。

早些时候，我们看到二次方程有$2, 1$$0$解。下图显示了这三种情况的抛物线示例。由于函数的解给出了图形的$x$-intercepts，因此$x$-intercepts的数量与解的数量相同。

以前，我们使用判别来确定这种形式的二次函数的解数$a x^{2}+b x+c=0$。现在我们可以使用判别器来告诉我们图上有多少$x$-intercepts。

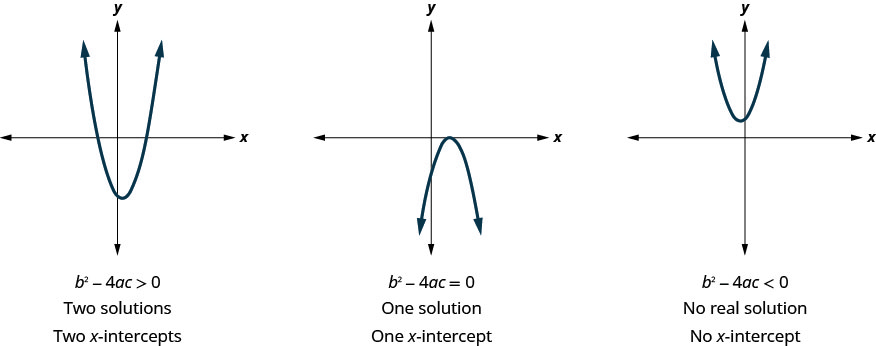
此图并排显示了三张图表。左边的图表显示了在 x y 坐标平面上绘制的向上开口的抛物线。抛物线的顶点位于 x 轴以下，抛物线在两个不同的点与 x 轴交叉。如果 b 平方减去 4 a c 大于 0，则二次方程 a x 平方加 b x 加 c 等于 0 有两个解，抛物线的图形有 2 个 x 截距。中间的图形显示了在 x y 坐标平面上绘制的向下开口的抛物线。抛物线的顶点位于 x 轴上，这是抛物线和 x 轴之间的唯一交点。如果 b 平方减去 4 a c 等于 0，则二次方程 a x 平方加 b x 加 c 等于 0 有一个解，抛物线的图形有 1 x 截距。右图显示了在 x y 坐标平面上绘制的向上开口的抛物线。抛物线的顶点位于 x 轴上方，抛物线不与 x 轴交叉。如果 b 平方减去 4 a c 小于 0，则二次方程 a x 平方加 b x 加 c 等于 0 没有解，抛物线的图形没有 x 截距。

在你找到$x$-intercepts的值之前，你可能需要评估判别值，这样你就可以知道预期会有多少解。

示例$\PageIndex{5}$

找出函数抛物线的截距$f(x)=5 x^{2}+x+4$。

解决方案：

	$。$
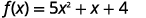要找到$y$-截距$x=0$，让我们求解$f(x)$。	$。$
	$。$
	那么$x=0$，什么时候$f(0)=4$。 $y$-截距是重点$(0,4)$。
要找到$x$-截距$f(x)=0$，让我们求解$x$。	$。$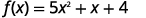
	$。$
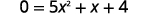找出判别值来预测解的数量，这也是$x$-intercepts的数量。
$\begin{array}{c}{b^{2}-4 a c} \\ {1^{2}-4 \cdot 5 \cdot 4} \\ {1-80} \\ {-79}\end{array}$
	由于判别值为负，因此该方程没有真正的解。没有$x$-intercepts。

练习$\PageIndex{9}$

找出函数为的抛物线的截距$f(x)=3 x^{2}+4 x+4$。

回答: $y$-截距：$(0,4)$没有$x$-截距

练习$\PageIndex{10}$

找出其功能为的抛物线的截距$f(x)=x^{2}-4 x-5$

回答: $y$-拦截：$(0,-5)$$x$-拦截$(-1,0),(5,0)$

使用属性绘制二次函数图

现在我们有了绘制二次函数所需的所有片段。我们只需要把它们放在一起。在下一个示例中，我们将看到如何执行此操作。

示例$\PageIndex{6}$ How to Graph a Quadratic Function Using Properties

使用$f(x)=x^{2}-6x+8$其属性绘制图表。

解决方案：

第 1 步：确定抛物线是向上还是向下打开。	看看$a$方程式$f(x)=x^{2}-6x+8$ 由于$a$为正值，抛物线向上打开。	$f(x)=x^{2}-6x+8$ $\color{red}{a=1, b=-6, c=8}$ 抛物线向上打开。
步骤 2：找到对称轴。	$f(x)=x^{2}-6x+8$ 对称轴是直线$x=-\frac{b}{2 a}$。	对称轴 $x=-\frac{b}{2 a}$ $x=-\frac{(-6)}{2 \cdot 1}$ $x=3$ 对称轴是直线$x=3$。
步骤 3：找到顶点。	顶点位于对称轴上。替换$x=3$到函数中。	顶点 $f(x)=x^{2}-6x+8$ $f(3)=(\color{red}{3}\color{black}{)}^{2}-6(\color{red}{3}\color{black}{)}+8$ $f(3)=-1$ 顶点是$(3,-1)$。
第 4 步：找到$y$截距。在对称轴上找到$y$与-截距对称的点。	我们发现$f(0)$。我们使用对称轴来找到一个与$y$-intercept对称的点。 $y$-截距是$3$指对称轴左边的单位$x=3$。对称轴右侧的点$3$单位有$x=6$。	$y$-截距 $f(x)=x^{2}-6 x+8$ $f(0)=(\color{red}{0}\color{black}{)}^{2}-6(\color{red}{0}\color{black}{)}+8$ $f(0)=8$ $y$-截距为$(0,8)$。指向对称点到$y$-截距：重点是$(6,8)$。
第 5 步：找到$x$-intercepts。如果需要，可以找到其他积分。	我们解决$f(x)=0$。我们可以通过分解求解这个二次方程。	$x$-拦截 $f(x)=x^{2}-6 x+8$ $\color{red}{0}\color{black}{=}x^{2}-6x+8$ $\color{red}{0}\color{black}{=}(x-2)(x-4)$ $x=2 or x=4$ $x$-intercepts 是$(2,0)$和$(4,0)$。
第 6 步：绘制抛物线图。	我们将顶点、截距和点绘制成与$y$-intercept对称的图形。我们将这些$5$点连接起来绘制抛物线。	$屏幕截图 (1) .png$

练习$\PageIndex{11}$

使用$f(x)=x^{2}+2x-8$其属性绘制图表。

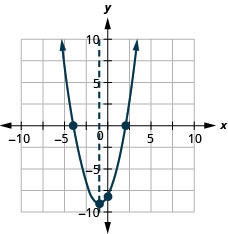
回答: $此图显示了在 x y 坐标平面上绘制的向上开口的抛物线。飞机的 x 轴从负 10 延伸到 10。飞机的 y 轴从负 10 延伸到 10。对称轴 x 等于负 1，以虚线绘制。抛物线的顶点位于（负 1，负 9）。抛物线的 y 截距是点（0，负 8）。抛物线的 x 截距是点（负 4、0）和（4、0）。$

练习$\PageIndex{12}$

使用$f(x)=x^{2}-8x+12$其属性绘制图表。

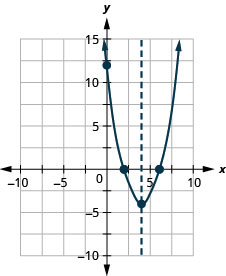
回答: $此图显示了在 x y 坐标平面上绘制的向上开口的抛物线。飞机的 x 轴从负 10 延伸到 10。飞机的 y 轴从负 10 延伸到 15。对称轴 x 等于 4，以虚线绘制。抛物线的顶点位于 (4，负 4)。抛物线的 y 截距是点 (0, 12)。抛物线的 x 截距是点 (2, 0) 和 (6, 0)。$

我们在此处列出了绘制二次函数图所要采取的步骤。

使用属性绘制二次函数的图表

确定抛物线是向上还是向下打开。
找到对称轴的方程。
找到顶点。
找到$y$截距。在对称轴上找到$y$与-截距对称的点。
找到$x$-截图。如果需要，可以找到其他积分。
绘制抛物线图。

通过分解，我们能够在上一个示例中找到$x$-intercepts。在下一个示例中，我们也通过分解找到了$x$-intercepts。

示例$\PageIndex{7}$

使用$f(x)=-x^{2}+6 x-9$其属性绘制图表。

解决方案：

	$。$
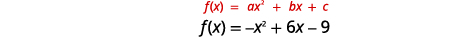$a$既然$-1$如此，抛物线向下打开。
	$。$
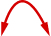要找到对称轴的方程，请使用$x=-\frac{b}{2 a}$。	$x=-\frac{b}{2 a}$
	$x=-\frac{6}{2(-1)}$
	$x=3$
	对称轴是$x=3$。顶点在线上$x=3$。
	$。$
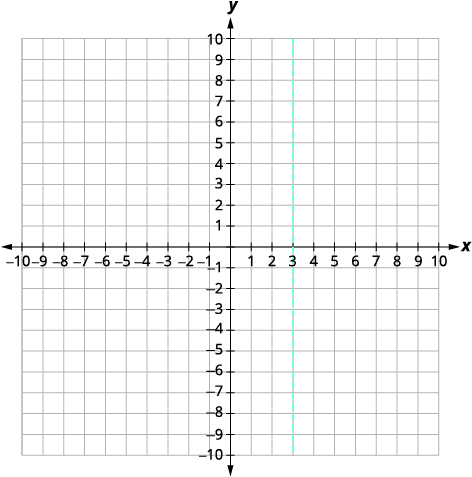查找$f(3)$。	$f(x)=-x^{2}+6 x-9$
	$。$
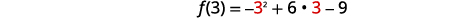	$f(3)=-9+18-9$
	$f(3)=0$
	顶点是$(3,0)$。
	$。$
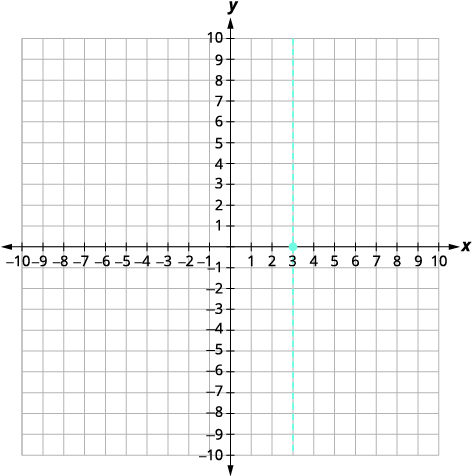$y$-截距发生在$x=0$. 查找$f(0)$。	$f(x)=-x^{2}+6 x-9$
替代$x=0$。	$。$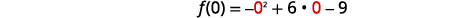
简化。	$f(0)=-9$
该点$(0,-9)$位于对称线左侧的三个单位。对称线右边三个单位的点是$(6,-9)$。	$。$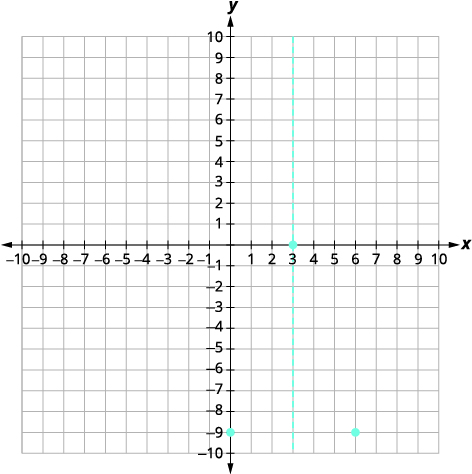
	与$y$-截距对称的点是$(6,-9)$
$x$-截距发生在$f(x)=0$.	$。$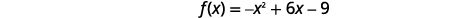
查找$f(x)=0$。	$。$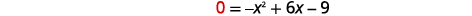
将 GCF 考虑在内。	$。$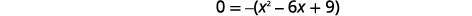
将三项式分解为因子。	$。$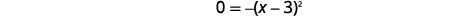
求解$x$。	$。$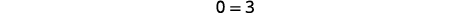
将各点连接起来，绘制抛物线图。	$。$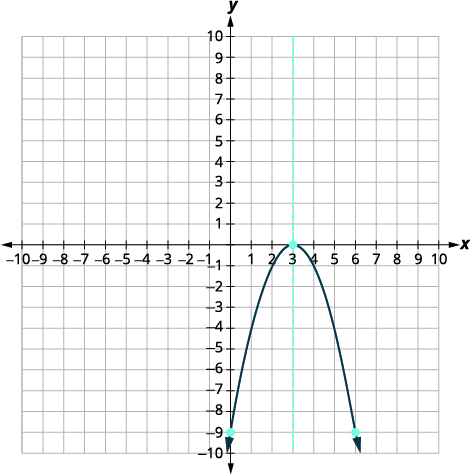

练习$\PageIndex{13}$

使用$f(x)=3 x^{2}+12 x-12$其属性绘制图表。

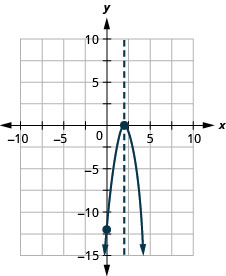
回答: $此图显示了在 x y 坐标平面上绘制的向下开口的抛物线。飞机的 x 轴从负 10 延伸到 10。飞机的 y 轴从负 15 延伸到 10。抛物线在 (2, 0) 处有一个顶点。绘制 y 截距（0，负 12）以及对称轴 x 等于 2。$

练习$\PageIndex{14}$

使用$f(x)=4 x^{2}+24 x+36$其属性绘制图表。

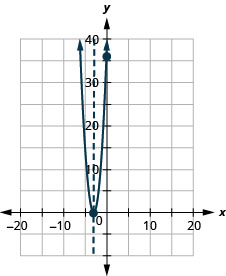
回答: $此图显示了在 x y 坐标平面上绘制的向上开口的抛物线。飞机的 x 轴从负 30 延伸到 20。飞机的 y 轴从负 10 延伸到 40。抛物线的顶点位于（负 3, 0）。绘制了 y 截距 (0, 36) 以及对称轴 x 等于负 3。$

对于的图$f(x)=-x^{2}+6 x-9$，顶点和$x$截距是同一个点。还记得判别是如何确定二次方程解数的吗？方程的判别$0=-x^{2}+6x-9$是$0$，所以只有一个解。这意味着只有一个$x$截距，它是抛物线的顶点。

你希望在图表上看到多少$x$-intercepts$f(x)=x^{2}+4 x+5$？

示例$\PageIndex{8}$

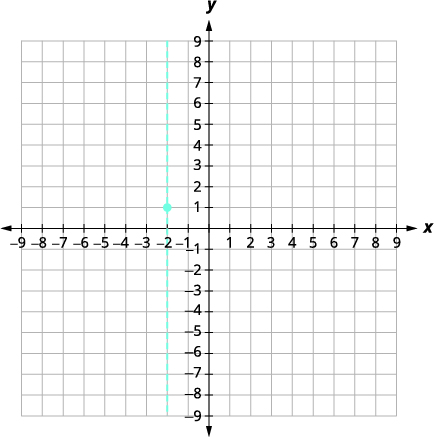
使用$f(x)=x^{2}+4 x+5$其属性绘制图表。

解决方案：

	$。$
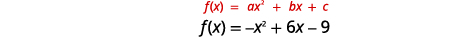$a$既然$-1$如此，抛物线向下打开。
	$。$
要找到对称轴的方程，请使用$x=-\frac{b}{2 a}$。	$。$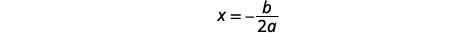
	$。$
	$。$
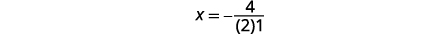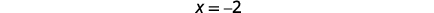	对称轴的方程为\ (x=-2)。
	$。$
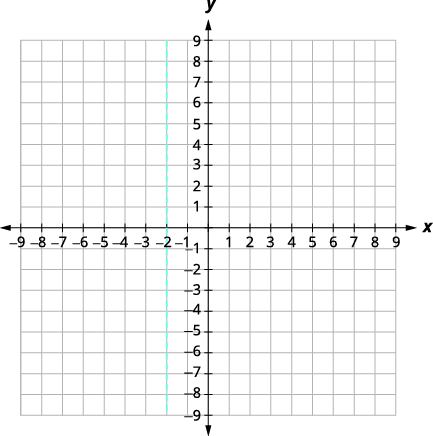顶点在线上$x=-2$。
找出$f(x)$时间$x=-2$。	$。$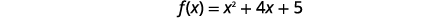
	$。$
	$。$
	$。$
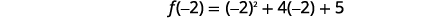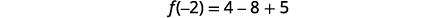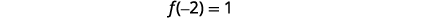	顶点是$(-2,1)$。
	$。$
$y$-截距发生在$x=0$.	$。$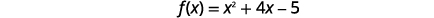
查找$f(0)$。	$。$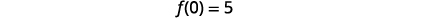
简化。	$。$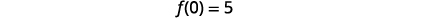
	$y$-截距为$(0,5)$。
该点$(-4,5)$位于对称线左侧的两个单位。指向对称线右边单位的点是\ ((0,5)\。	$。$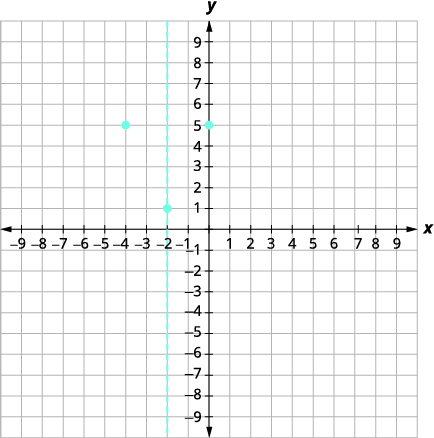
	与$y$-截距对称的点是$(-4,5)$。
$x$-截距发生在$f(x)=0$.	$。$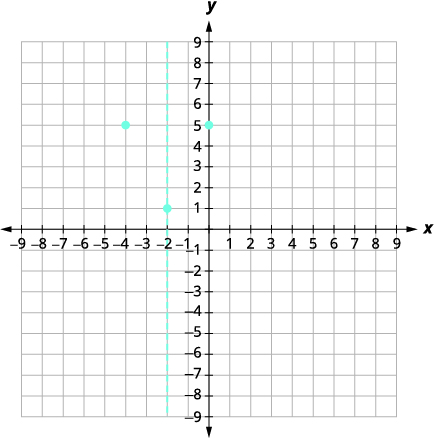
查找$f(x)=0$。	$。$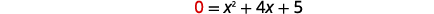
测试判别值。
	$。$
	$。$
	$。$
	$。$
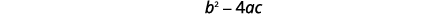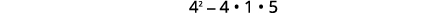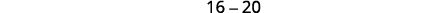由于判别值为负，因此没有真正的解，因此没有$x$-intercept。
将各点连接起来，绘制抛物线图。您可能需要再选择两个点以获得更高的精度。	$。$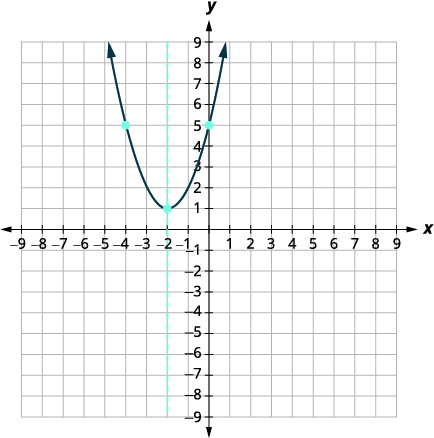

练习$\PageIndex{15}$

使用$f(x)=x^{2}-2 x+3$其属性绘制图表。

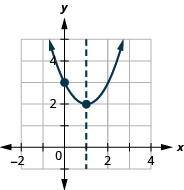
回答: $此图显示了在 x y 坐标平面上绘制的向上开口的抛物线。平面的 x 轴从负 2 延伸到 4。飞机的 y 轴从负 1 延伸到 5。抛物线在 (1, 2) 处有一个顶点。 y 截距 (0, 3) 与对称线一样绘制，x 等于 1。$

练习$\PageIndex{16}$

使用$f(x)=-3x^{2}-6 x-4$其属性绘制图表。

回答: $此图显示了在 x y 坐标平面上绘制的向下开口的抛物线。平面的 x 轴从负 4 延伸到 2。飞机的 y 轴从负 5 延伸到 1。抛物线的顶点位于（负 1，负 2）。 y 截距（0，负 4）与对称线一样绘制，x 等于负 1。$

通过查找找到$y$截距$f(0)$很容易，不是吗？有时我们需要使用二次公式来找到$x$-intercepts。

示例$\PageIndex{9}$

使用$f(x)=2 x^{2}-4 x-3$其属性绘制图表。

解决方案：

	$。$
$a$既然如此$2$，抛物线向上打开。	$。$
要找到对称轴的方程，请使用$x=-\frac{b}{2 a}$。	$x=-\frac{b}{2 a}$
	$x=-\frac{-4}{2 \cdot 2}$
	$x=1$
	对称轴的方程为$x=1$。
顶点在线上$x=1$。	$f(x)=2 x^{2}-4 x-3$
查找$f(1)$。	$。$
	$f(1)=2-4-3$
	\ (\ f (1) =-5)
	顶点是$(1,-5)$。
$y$-截距发生在$x=0$.	$f(x)=2 x^{2}-4 x-3$
查找$f(0)$。	$。$
简化。	$f(0)=-3$
	$y$-截距为$(0,-3)$。
该点$(0,-3)$位于对称线左侧一个单位。	与$y$-截距对称的点是$(2,-3)$
对称线右边一个单位的点是$(2,3)$。
$x$-截距发生在$y=0$.	$f(x)=2 x^{2}-4 x-3$
查找$f(x)=0$。	$。$
使用二次方程式。	$x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}$
用$a,b$和的值代替$c$。	$x=\frac{-(-4) \pm \sqrt{(-4)^{2}-4(2)(3)}}{2(2)}$
简化。	$x=\frac{-4 \pm \sqrt{16+24}}{4}$
在激进内部进行简化。	$x=\frac{4 \pm \sqrt{40}}{4}$
简化激进。	$x=\frac{4 \pm 2 \sqrt{10}}{4}$
将 GCF 考虑在内。	$x=\frac{2(2 \pm \sqrt{10})}{4}$
移除常见因素。	$x=\frac{2 \pm \sqrt{10}}{2}$
写成两个方程式。	$x=\frac{2+\sqrt{10}}{2}, \quad x=\frac{2-\sqrt{10}}{2}$
对数值进行近似值。	$x \approx 2.5, \quad x \approx-0.6$
	$x$-intercepts 的近似值为$(2.5,0)$和$(-0.6,0)$。
使用找到的点绘制抛物线图。	$。$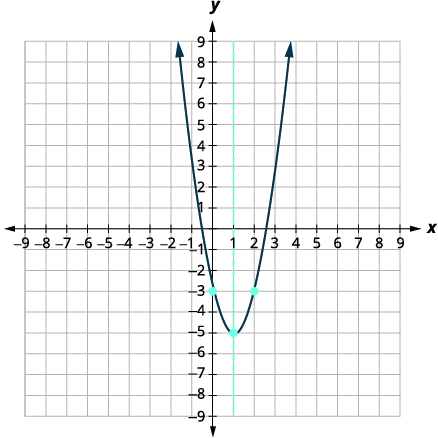

练习$\PageIndex{17}$

使用$f(x)=5 x^{2}+10 x+3$其属性绘制图表。

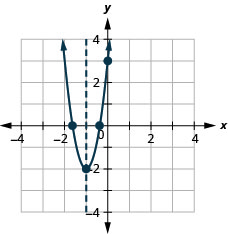
回答: $此图显示了在 x y 坐标平面上绘制的向上开口的抛物线。飞机的 x 轴从负 4 延伸到 4。飞机的 y 轴从负 4 延伸到 4。对称轴 x 等于负 1，以虚线绘制。抛物线的顶点位于（负 1，负 2）。抛物线的 y 截距是点 (0, 3)。抛物线的 x 截距大约为（负 1.6、0）和（负 0.4、0）。$

练习$\PageIndex{18}$

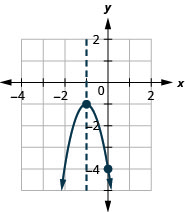
使用$f(x)=-3 x^{2}-6 x+5$其属性绘制图表。

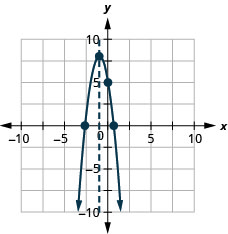
回答: $此图显示了在 x y 坐标平面上绘制的向下开口的抛物线。飞机的 x 轴从负 10 延伸到 10。飞机的 y 轴从负 10 延伸到 10。对称轴 x 等于负 1，以虚线绘制。抛物线的顶点位于（负 1, 8）。抛物线的 y 截距是点 (0, 5)。抛物线的 x 截距大约为（负 2.6、0）和（0.6、0）。$

求解最大值和最小值应用程序

知道抛物线的顶点是抛物线的最低点或最高点，这为我们提供了一种确定二次函数的最小值或最大值的简便方法。顶点的 y 坐标是向上打开的抛物线的最小值。它是向下打开的抛物线的最大值。参见图 9.6.124。

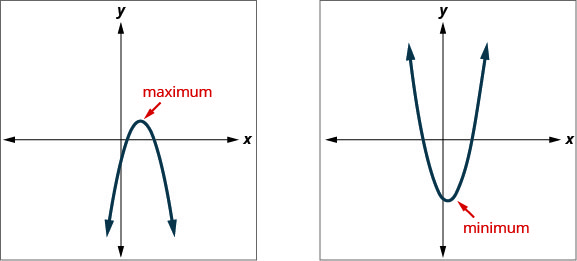
此图并排显示了 2 张图表。左图显示了在 x y 平面上绘制的向下开口的抛物线。箭头指向标签最大值的顶点。右图显示了在 x y 平面上绘制的向上开口的抛物线。箭头指向带有最小标签的顶点。 — 图 9.6.124

二次函数的最小值或最大值

二次函数图形顶点的 y 坐标是

如果抛物线向上打开，则二次方程@@ 的最小值。
如果抛物线向下打开，则二次方程@@ 的最大值。

示例$\PageIndex{10}$

求二次函数的最小值或最大值$f(x)=x^{2}+2 x-8$。

解决方案：

	$f(x)=x^{2}+2 x-8$
由于$a$为正值，抛物线向上打开。二次方程具有最小值。
找到对称轴的方程。	$x=-\frac{b}{2 a}$
	$x=-\frac{2}{2 \times 1}$
	$x=-1$
	对称轴的方程为$x=-1$。
顶点在线上$x=-1$。	$f(x)=x^{2}+2 x-8$
查找$f(-1)$。	$。$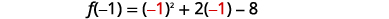
	$f(-1)=1-2-8$
	$f(-1)=-9$
	顶点是$(-1,-9)$。
由于抛物线具有最小值，因此顶点的$y$坐标是二次方程的最小$y$值。二次曲线的最小值为$-9$，它出现在何时$x=-1$。
	$。$

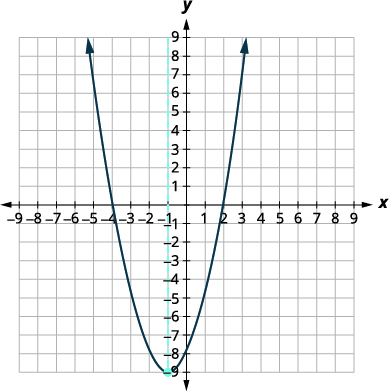显示图表以验证结果。

练习$\PageIndex{19}$

求二次函数的最大值或最小值$f(x)=x^{2}-8 x+12$。

回答: 二次函数的最小值为$−4$，它发生在什么时候$x=4$。

练习$\PageIndex{20}$

求二次函数的最大值或最小值$f(x)=-4 x^{2}+16 x-11$。

回答: 二次函数的最大值为，它发生在什么时候$x=2$。$5$

我们已经使用了这个公式

$h(t)=-16 t^{2}+v_{0} t+h_{0}$

计算以英尺为单位的物体在$t$秒后以初始速度向上射入空中的高度。$h$$v_{0}$

这个公式是二次函数，所以它的图形是一个抛物线。通过求解顶点的坐标$(t,h)$，我们可以得出物体需要多长时间才能达到其最大高度。然后我们可以计算出最大高度。

示例$\PageIndex{11}$

二次方程$h(t)=-16 t^{2}+176 t+4$模拟了排球从英尺高处直向上击球的高度，速度$4$英$176$尺/秒。

排球需要多少秒才能达到最大高度？
找到排球的最大高度。

解决方案：

$h(t)=-16 t^{2}+176 t+4$

由于$a$为负值，抛物线向下打开。二次函数具有最大值。

a. 找到对称轴的方程。

$\begin{array}{l}{t=-\frac{b}{2 a}} \\ {t=-\frac{176}{2(-16)}} \\ {t=5.5}\end{array}$

对称轴的方程为$t=5.5$。

顶点在线上$t=5.5$。

最大值以$t=5.5$秒为单位。

b. 查找$h(5.5)$。

$\begin{array}{l}{h(t)=-16 t^{2}+176 t+4} \\ {h(t)=-16(5.5)^{2}+176(5.5)+4}\end{array}$

使用计算器进行简化。

$h(t)=488$

顶点是$(5.5,488)$。

由于抛物线具有最大值，因此顶点的$h$坐标是二次函数的最大值。

二次曲线的最大值是$488$英尺，它在$t=5.5$秒钟时出现。

$5.5$几秒钟后，排球将达到其最大$488$英尺高度。

练习$\PageIndex{21}$

求解，将答案四舍五入到最接近的十分之一。

二次函数$h(t)=-16 t^{2}+128 t+32$用于计算以英尺$128$ /秒的速度从$32$英尺高度向上投掷的石头的高度。宝石需要多长时间才能达到其最大高度？最大高度是多少？

回答: 石头需要$4$几秒钟才能达到其最大高度（$288$英尺）。

练习$\PageIndex{22}$

玩具火箭以$208$英尺/秒的速度从地面向上投掷的路径由的二次函数建模$h(t)=-16 t^{2}+208 t$。火箭何时会达到最大高度？最大高度是多少？

回答: 火箭需要$6.5$几秒钟才能达到其最大$676$英尺高度。

关键概念

抛物线方向
- 对于二次函数的图形$f(x)=a x^{2}+b x+c$，如果
  - $a>0$，抛物线向上打开。
  - $a<0$，抛物线向下打开。
对称轴和抛物线顶点函数的图形$f(x)=a x^{2}+b x+c$是一个抛物线，其中：
- 对称轴是垂直线$x=-\frac{b}{2 a}$。
- 顶点是对称轴上的一个点，所以它的$x$-坐标是$-\frac{b}{2 a}$。
- 顶点$y$的坐标是通过代$x=-\frac{b}{2 a}$入二次方程来找到的。
找出抛物线的截取物
- 要找到其功能为的抛物线的截距$f(x)=a x^{2}+b x+c$：
  - $y$-截距
    - 让我们$x=0$来解决吧$f(x)$。
  - $x$-拦截
    - 让我们$f(x)=0$来解决吧$x$.
如何使用属性绘制二次函数图。
1. 确定抛物线是向上还是向下打开。
2. 找到对称轴的方程。
3. 找到顶点。
4. 找到$y$截距。在对称轴上找到与 y 截距对称的点。
5. 找到$x$-截图。如果需要，可以找到其他积分。
6. 绘制抛物线图。
二次方程的最小值或最大值
- 二次方程图形顶点的$y$坐标是
- 如果抛物线向上打开，则二次方程@@ 的最小值。
- 如果抛物线向下打开，则二次方程@@ 的最大值。

词汇表

二次函数: 二次函数，其中$a, b$，和$c$是实数$a≠0$，是形式的函数$f(x)=ax^{2}+bx+c$。

	$。$
对称轴是垂直线\(x=-\frac{b}{2 a}\)。
将这些值替换\(a,b\)到方程中。	\(x=-\frac{-6}{2 \cdot 3}\)
简化。	\(x=1\)
	对称轴是直线\(x=1\)。

	\(f(x)=3 x^{2}-6 x+2\)
顶点是对称线上的一个点，所以它的\(x\)-坐标将是\(x=1\)。查找\(f(1)\)。	$。$
简化。	$。$
结果是\(y\)-坐标。	\(f(1)=-1\)
	顶点是\((1,-1)\)。

	\(f(x)=x^{2}+4 x+3\)
让\(f(x)=0\)。	\(\color{red}0\color{black}=x^{2}+4 x+3\)
因子。	\(0=(x+1)(x+3)\)
使用 “零积分” 属性。	\(x+1=0 \quad x+3=0\)
解决。	\(x=-1 \quad x=-3\)
	\(x\)-intercepts 是\((-1,0)\)和\((-3,0)\)。

	\(f(x)=-x^{2}+4 x+3\)
让\(f(x)=0\)。	\(\color{red}0 \color{black}=-x^{2}+4 x+3\)
这个二次不分解，所以我们使用二次方程式。	\(x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\)
\(a=-1, b=4, c=3\)	\(x=\frac{-4 \pm \sqrt{4^{2}-4(-1)(3)}}{2(-1)}\)
简化。	\(x=\frac{-4 \pm \sqrt{28}}{-2}\)
	\(x=\frac{-4 \pm 2 \sqrt{7}}{-2}\)
	\(x=\frac{-2(2 \pm \sqrt{7})}{-2}\)
	\(x=2 \pm \sqrt{7}\)
	\(x\)-intercepts 是\((2+\sqrt{7}, 0)\)和\((2-\sqrt{7}, 0)\)。

要找到\(y\)-截距\(x=0\)，让我们求解\(f(x)\)。	\(f(x)=x^{2}-2 x-8\)
	\(f(0)=\color{red}0\color{black}^{2}-2 \cdot \color{red}0 \color{black}-8\)
	\(f(0)=-8\)
	那么\(x=0\)，什么时候\(f(0)=-8\)。 \(y\)-截距是重点\((0,-8)\)。
要找到\(x\)-截距\(f(x)=0\)，让我们求解\(x\)。	\(f(x)=x^{2}-2 x-8\)
	\(0=x^{2}-2 x-8\)
通过分解求解。	\(0=(x-4)(x+2)\)
	\(0=x-4 \quad 0=x+2\)
	\(4=x \quad-2=x\)
	什么时候\(f(x)=0\)，然后\(x=4\)或\(x=-2\)。 \(x\)-intercepts 是积分\((4,0)\)和\((-2,0)\)。

定义\(\PageIndex{1}\)

示例\(\PageIndex{1}\)

练习\(\PageIndex{1}\)

练习\(\PageIndex{2}\)

定义\(\PageIndex{2}\)

示例\(\PageIndex{2}\)

练习\(\PageIndex{3}\)

练习\(\PageIndex{4}\)

示例\(\PageIndex{3}\)

练习\(\PageIndex{5}\)

练习\(\PageIndex{6}\)

示例\(\PageIndex{4}\)

练习\(\PageIndex{7}\)

练习\(\PageIndex{8}\)

示例\(\PageIndex{5}\)

练习\(\PageIndex{9}\)

练习\(\PageIndex{10}\)

示例\(\PageIndex{6}\) How to Graph a Quadratic Function Using Properties

练习\(\PageIndex{11}\)

练习\(\PageIndex{12}\)

示例\(\PageIndex{7}\)

练习\(\PageIndex{13}\)

练习\(\PageIndex{14}\)

示例\(\PageIndex{8}\)

练习\(\PageIndex{15}\)

练习\(\PageIndex{16}\)

示例\(\PageIndex{9}\)

练习\(\PageIndex{17}\)

练习\(\PageIndex{18}\)

示例\(\PageIndex{10}\)

练习\(\PageIndex{19}\)

练习\(\PageIndex{20}\)

示例\(\PageIndex{11}\)

练习\(\PageIndex{21}\)

练习\(\PageIndex{22}\)

选择整数值\(x\)，将它们替换到方程中，然后简化即可查找\(f(x)\)。在图表中记录有序货币对的值。	$。$
绘制这些点，然后用平滑曲线将它们连接起来。结果将是函数的图形\(f(x)=x^{2}-1\)。	$。$

第 1 步：确定抛物线是向上还是向下打开。	看看\(a\)方程式\(f(x)=x^{2}-6x+8\) 由于\(a\)为正值，抛物线向上打开。	\(f(x)=x^{2}-6x+8\) \(\color{red}{a=1, b=-6, c=8}\) 抛物线向上打开。
步骤 2：找到对称轴。	\(f(x)=x^{2}-6x+8\) 对称轴是直线\(x=-\frac{b}{2 a}\)。	对称轴 \(x=-\frac{b}{2 a}\) \(x=-\frac{(-6)}{2 \cdot 1}\) \(x=3\) 对称轴是直线\(x=3\)。
步骤 3：找到顶点。	顶点位于对称轴上。替换\(x=3\)到函数中。	顶点 \(f(x)=x^{2}-6x+8\) \(f(3)=(\color{red}{3}\color{black}{)}^{2}-6(\color{red}{3}\color{black}{)}+8\) \(f(3)=-1\) 顶点是\((3,-1)\)。
第 4 步：找到\(y\)截距。在对称轴上找到\(y\)与-截距对称的点。	我们发现\(f(0)\)。我们使用对称轴来找到一个与\(y\)-intercept对称的点。 \(y\)-截距是\(3\)指对称轴左边的单位\(x=3\)。对称轴右侧的点\(3\)单位有\(x=6\)。	\(y\)-截距 \(f(x)=x^{2}-6 x+8\) \(f(0)=(\color{red}{0}\color{black}{)}^{2}-6(\color{red}{0}\color{black}{)}+8\) \(f(0)=8\) \(y\)-截距为\((0,8)\)。指向对称点到\(y\)-截距：重点是\((6,8)\)。
第 5 步：找到\(x\)-intercepts。如果需要，可以找到其他积分。	我们解决\(f(x)=0\)。我们可以通过分解求解这个二次方程。	\(x\)-拦截 \(f(x)=x^{2}-6 x+8\) \(\color{red}{0}\color{black}{=}x^{2}-6x+8\) \(\color{red}{0}\color{black}{=}(x-2)(x-4)\) \(x=2 or x=4\) \(x\)-intercepts 是\((2,0)\)和\((4,0)\)。
第 6 步：绘制抛物线图。	我们将顶点、截距和点绘制成与\(y\)-intercept对称的图形。我们将这些\(5\)点连接起来绘制抛物线。	$屏幕截图 (1) .png$

	$。$
\(a\)既然\(-1\)如此，抛物线向下打开。
	$。$
要找到对称轴的方程，请使用\(x=-\frac{b}{2 a}\)。	\(x=-\frac{b}{2 a}\)
	\(x=-\frac{6}{2(-1)}\)
	\(x=3\)
	对称轴是\(x=3\)。顶点在线上\(x=3\)。
	$。$
查找\(f(3)\)。	\(f(x)=-x^{2}+6 x-9\)
	$。$
	\(f(3)=-9+18-9\)
	\(f(3)=0\)
	顶点是\((3,0)\)。
	$。$
\(y\)-截距发生在\(x=0\). 查找\(f(0)\)。	\(f(x)=-x^{2}+6 x-9\)
替代\(x=0\)。	$。$
简化。	\(f(0)=-9\)
该点\((0,-9)\)位于对称线左侧的三个单位。对称线右边三个单位的点是\((6,-9)\)。	$。$
	与\(y\)-截距对称的点是\((6,-9)\)
\(x\)-截距发生在\(f(x)=0\).	$。$
查找\(f(x)=0\)。	$。$
将 GCF 考虑在内。	$。$
将三项式分解为因子。	$。$
求解\(x\)。	$。$
将各点连接起来，绘制抛物线图。	$。$

	$。$
\(a\)既然如此\(2\)，抛物线向上打开。	$。$
要找到对称轴的方程，请使用\(x=-\frac{b}{2 a}\)。	\(x=-\frac{b}{2 a}\)
	\(x=-\frac{-4}{2 \cdot 2}\)
	\(x=1\)
	对称轴的方程为\(x=1\)。
顶点在线上\(x=1\)。	\(f(x)=2 x^{2}-4 x-3\)
查找\(f(1)\)。	$。$
	\(f(1)=2-4-3\)
	\ (\ f (1) =-5)
	顶点是\((1,-5)\)。
\(y\)-截距发生在\(x=0\).	\(f(x)=2 x^{2}-4 x-3\)
查找\(f(0)\)。	$。$
简化。	\(f(0)=-3\)
	\(y\)-截距为\((0,-3)\)。
该点\((0,-3)\)位于对称线左侧一个单位。	与\(y\)-截距对称的点是\((2,-3)\)
对称线右边一个单位的点是\((2,3)\)。
\(x\)-截距发生在\(y=0\).	\(f(x)=2 x^{2}-4 x-3\)
查找\(f(x)=0\)。	$。$
使用二次方程式。	\(x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\)
用\(a,b\)和的值代替\(c\)。	\(x=\frac{-(-4) \pm \sqrt{(-4)^{2}-4(2)(3)}}{2(2)}\)
简化。	\(x=\frac{-4 \pm \sqrt{16+24}}{4}\)
在激进内部进行简化。	\(x=\frac{4 \pm \sqrt{40}}{4}\)
简化激进。	\(x=\frac{4 \pm 2 \sqrt{10}}{4}\)
将 GCF 考虑在内。	\(x=\frac{2(2 \pm \sqrt{10})}{4}\)
移除常见因素。	\(x=\frac{2 \pm \sqrt{10}}{2}\)
写成两个方程式。	\(x=\frac{2+\sqrt{10}}{2}, \quad x=\frac{2-\sqrt{10}}{2}\)
对数值进行近似值。	\(x \approx 2.5, \quad x \approx-0.6\)
	\(x\)-intercepts 的近似值为\((2.5,0)\)和\((-0.6,0)\)。
使用找到的点绘制抛物线图。	$。$

	\(f(x)=x^{2}+2 x-8\)
由于\(a\)为正值，抛物线向上打开。二次方程具有最小值。
找到对称轴的方程。	\(x=-\frac{b}{2 a}\)
	\(x=-\frac{2}{2 \times 1}\)
	\(x=-1\)
	对称轴的方程为\(x=-1\)。
顶点在线上\(x=-1\)。	\(f(x)=x^{2}+2 x-8\)
查找\(f(-1)\)。	$。$
	\(f(-1)=1-2-8\)
	\(f(-1)=-9\)
	顶点是\((-1,-9)\)。
由于抛物线具有最小值，因此顶点的\(y\)坐标是二次方程的最小\(y\)值。二次曲线的最小值为\(-9\)，它出现在何时\(x=-1\)。
	$。$