9.6：求解二次方程的应用

Last updated
Save as PDF

Page ID: 204113

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

学习目标

在本节结束时，您将能够：

求解由二次方程建模的应用程序

在开始之前，请参加这个准备测验。

两个连续奇数的总和为$−100$。找到数字。
如果你错过了这个问题，请查看示例 2.18。
解决：$\frac{2}{x+1}+\frac{1}{x-1}=\frac{1}{x^{2}-1}$。
如果您错过了此问题，请查看示例 7.35。
找出腿部$5$英寸和$12$英寸的直角三角形的斜边长度。
如果你错过了这个问题，请查看示例 2.34。

求解由二次方程建模的应用程序

我们之前求解了一些由二次方程建模的应用程序，当时我们唯一的求解方法是分解。现在我们有了更多的求解二次方程的方法，我们再来看一下应用。

让我们先总结一下现在求解二次方程的方法。

求解二次方程的方法

保理
平方根属性
完成方块
二次方程式

在求解每个方程时，请选择最便于解决问题的方法。提醒一下，我们将在这里复制我们通常的问题解决策略，以便我们可以按照步骤操作。

使用问题解决策略

阅读问题。确保所有文字和想法都被理解。
确定我们在寻找什么。
说出我们要找的东西。选择一个变量来表示该数量。
翻译成方程式。用一句话用所有重要信息重述问题可能会有所帮助。然后，将英语句子翻译成代数方程。
使用代数技术求解方程。
检查问题中的答案并确保答案合理。
用完整的句子@@ 回答问题。

通过使用线性方程对情况进行建模，我们已经求解了涉及连续偶数和奇数整数的数字应用程序。请记住，我们注意到每个偶数整数都$2$比它前面的数字大。如果我们调用第一个$n$，那么下一个是$n+2$。下一个是$n+2+2$或$n+4$。当我们使用奇数整数时也是如此。下面显示了一组偶数和一组奇数整数。

$\begin{array}{cl}{}&{\text{Consecutive even integers}}\\{}& {64,66,68}\\ {n} & {1^{\text { st }} \text { even integer }} \\ {n+2} & {2^{\text { nd }} \text { consecutive even integer }} \\ {n+4} & {3^{\text { rd }} \text { consecutive even integer }}\end{array}$

$\begin{array}{cl}{}&{\text{Consecutive odd integers}}\\{}& {77,79,81}\\ {n} & {1^{\text { st }} \text { odd integer }} \\ {n+2} & {2^{\text { nd }} \text { consecutive odd integer }} \\ {n+4} & {3^{\text { rd }} \text { consecutive odd integer }}\end{array}$

奇数或偶数连续整数的某些应用是通过二次方程建模的。上面的表示法在你命名变量时会有所帮助。

示例$\PageIndex{1}$

两个连续奇数整数的乘积为$195$。找出整数。

解决方案：

第 1 步：阅读问题

第 2 步：确定我们在寻找什么。

我们正在寻找两个连续的奇数整数。

第 3 步：说出我们要找的内容。

假设$n=$第一个奇数整数。

$n+2=$下一个奇数整数。

第 4 步：转换为方程式。用一句话陈述问题。

“两个连续奇数整数的乘积是$195$。” 第一个奇数整数和第二个奇数整数的乘积为$195$。

翻译成方程式。

$n(n+2)=195$

步骤 5：求解方程。分发。

$n^{2}+2 n=195$

用标准形式写出方程式。

$n^{2}+2 n-195=0$

因子。

$(n+15)(n-13)=0$

使用 “零积分” 属性。

$n+15=0 \quad n-13=0$

求解每个方程。

$n=-15, \quad n=13$

有两个值$n$是解。这将为我们的解提供两对连续的奇数整数。

$\begin{array}{cc}{\text { First odd integer } n=13} & {\text { First odd integer } n=-15} \\ {\text { next odd integer } n+2} & {\text { next odd integer } n+2} \\ {13+2} & {-15+2} \\ {15} & {-13}\end{array}$

第 6 步：检查答案。

这些对能起作用吗？它们是连续的奇数整数吗？

$\begin{aligned} 13,15 & \text { yes } \\-13,-15 & \text { yes } \end{aligned}$

是他们的产品$195$吗？

$\begin{aligned} 13 \cdot 15 &=195 &\text{yes} \\-13(-15) &=195 & \text { yes } \end{aligned}$

第 7 步：回答问题。

乘积为的两个连续奇数整数$195$是$13,15$和$-13,-15$。

练习$\PageIndex{1}$

两个连续奇数整数的乘积为$99$。找出整数。

回答: 乘积为的两个连续奇数整数$99$是$9, 11$、和$−9, −11$。

练习$\PageIndex{2}$

两个连续偶数整数的乘积为$168$。找出整数。

回答: 乘积为$12, 14$和的两个连续偶数整数$−12, −14$。$128$

我们将使用三角形面积的公式来求解下一个示例。

定义$\PageIndex{1}$

三角形的面积

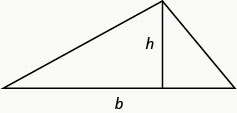
对于基数和高度的三角形$h$，面积由公式给出$A=\frac{1}{2} b h$。$b$$A$

三角形的图像。水平基边被标记为 b，标有 h 的线段垂直于底部，将其连接到相反的顶点。 — 图 9.5.1

回想一下，当我们求解几何应用时，绘制图形会很有帮助。

示例$\PageIndex{2}$

一位建筑师正在设计一家餐厅的入口通道。她想在门口上方放一扇三角窗。由于能源限制，窗户的面积只能为$120$平方英尺，建筑师希望底座的高度超过两倍。$4$ 找到窗户的底部和高度。

解决方案：

表 9.5.1
第 1 步：阅读问题。画一张照片。	$。$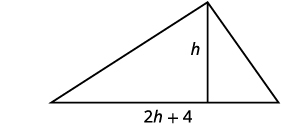
第 2 步：确定我们在寻找什么。	我们正在寻找底座和高度。
第 3 步：说出我们要找的内容。	假$h=$设三角形的高度。 $2h+4=$三角形的底部。
第 4 步：转换为方程式。我们知道这个地区。写出三角形面积的公式。	$A=\frac{1}{2} b h$
步骤 5：求解方程。在值中替换。	$120=\frac{1}{2}(2 h+4) h$
分发。	$120=h^{2}+2 h$
这是一个二次方程，用标准形式重写。	$h^{2}+2 h-120=0$
因子。	$(h-10)(h+12)=0$
使用 “零积分” 属性。	$h-10=0 \quad h+12=0$
简化。	$h=10, \quad \cancel{h=-12}$
因为$h$是窗口的高度，所以值是$h=-12$没有意义的。
三角形的高度$h=10$。
三角形的底部$2h+4$。 $2 \cdot 10+4$ $24$
第 6 步：检查答案。有高度$10$和底部的三角形$24$有面积$120$吗？是的。
第 7 步：回答问题。	三角窗的高度为$10$英尺，底部为$24$英尺。

练习$\PageIndex{3}$

找出一个三角形的底部和高度，该三角形的底部比其高度的六倍多四英寸，面$456$积为平方英寸。

回答: 三角形的高度为$12$英寸，底部为$76$英寸。

练习$\PageIndex{4}$

如果面积为$110$平方英尺的三角形的底部小于两倍高度的两倍，那么其底部的长度和高度是多少？

回答: 三角形的高度为$11$英尺，底部为$20$英尺。

在前两个示例中，二次公式中激进部分中的数字是一个完美的正方形，因此解是有理数。如果我们得到一个非理性数作为应用程序问题的解，我们将使用计算器来得到一个近似值。

我们将使用矩形面积的公式来求解下一个示例。

定义$\PageIndex{2}$

矩形的面积

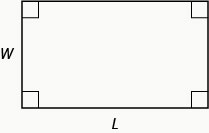
对于长度$L$、宽度均为的矩形$A$，面积由公式给出$A=LW$。$W$

该图显示了一个矩形。所有四个角度都标记为直角。较长的水平边标记为 L，较短的垂直边标记为 w。 — 图 9.5.3

示例$\PageIndex{3}$

迈克想在他的前院放一$150$平方英尺的人造草皮。这是他的房主协会允许的最大人造草坪面积。他想要一个长度小于宽度$3$乘以一英尺的矩形草皮区域。找到长度和宽度。四舍五入到最接近的十分之一英尺。

解决方案：

表 9.5.2
第 1 步：阅读问题。画一张照片。	$。$
第 2 步：确定我们在寻找什么。	我们正在寻找长度和宽度。
第 3 步：说出我们要找的内容。	假$w=$设矩形的宽度。 $3w-1=$矩形的长度
第 4 步：转换为方程式。我们知道这个地区。写出矩形面积的公式。	$。$
步骤 5：求解方程。在值中替换。	$。$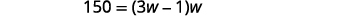
分发。	$。$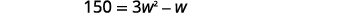
这是一个二次方程；用标准形式重写它。使用二次公式求解方程。	$。$
确定$a,b,c$值。	$。$
写下二次方程式。	$。$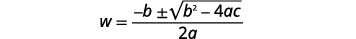
然后替换为的值$a,b,c$。	$。$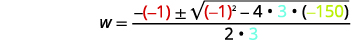
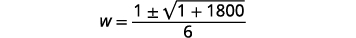
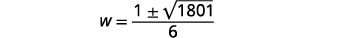
简化。	$。$ $。$ 图 9.5.13
重写以显示两个解决方案。	$。$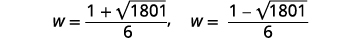
使用计算器估算答案。我们消除了宽度的负解。	$。$
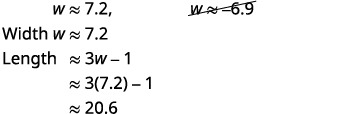第 6 步：检查答案。确保答案有意义。由于答案是近似的，因此该区域不会完全确定$150$。
第 7 步：回答问题。	矩形的宽度约为$7.2$英尺，长度约为$20.6$英尺。

练习$\PageIndex{5}$

$200$平方英尺的矩形菜园的长度比宽度的两倍小四英尺。找出花园的长度和宽度，精确到最接近的十分之一英尺。

回答: 花园的长度约为$18$英尺，宽度为$11$英尺.

练习$\PageIndex{6}$

矩形桌布的面积为$80$平方英尺。宽度比长度短一$5$英尺。桌布的长度和宽度是多少，最接近十分之一英尺？

回答: 桌布的长度约为$11.8$英尺，宽度为$6.8$英尺。

毕达哥拉斯定理给出了直角三角形的腿和斜边之间的关系。我们将使用毕达哥拉斯定理来求解下一个例子。

定义$\PageIndex{3}$

毕达哥拉斯定理

在任何直角三角形中，其中$a$和$b$是腿的长度，$c$是斜边的长度$a^{2}+b^{2}=c^{2}$。

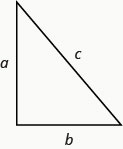
该图显示了带有水平和垂直支腿的直角三角形。垂直腿标记为 a。水平边标记为 b。斜边标记为 c。 — 图 9.5.16

示例$\PageIndex{4}$

Rene 正在设置节日灯光显示屏。他想做一棵两个直角三角形形状的 “树”，如下所示，两侧有两$10$英尺长的灯串可供使用。他会把灯固定在杆子的顶部和地上的两个木桩上。他希望杆子的高度与杆底到每个木桩的距离相同。杆子应该有多高？

解决方案：

表 9.5.3
第 1 步：阅读问题。画一张照片。	$。$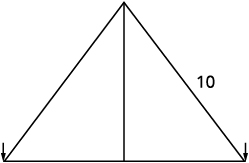
第 2 步：确定我们在寻找什么。	我们正在寻找杆子的高度。
第 3 步：说出我们要找的内容。	从杆子底部到任一木桩的距离与杆子的高度相同。假$x=$设杆子的高度。 $x=$从杆子到木桩的距离每边都是一个直角三角形。我们画了其中一张照片。 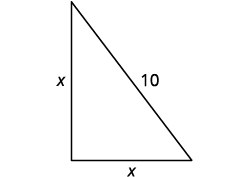$。$ 图 9.5.18
第 4 步：转换为方程式。我们可以使用毕达哥拉斯定理来求解$x$。写下毕达哥拉斯定理。	$a^{2}+b^{2}=c^{2}$
步骤 5：求解方程。替代。	$x^{2}+x^{2}=10^{2}$
简化。	$2 x^{2}=100$
除$2$以分离变量。	$\frac{2 x^{2}}{2}=\frac{100}{2}$
简化。	$x^{2}=50$
使用平方根属性。	$x=\pm \sqrt{50}$
简化激进。	$x=\pm 5 \sqrt{2}$
重写以显示两个解决方案。	$x=5 \sqrt{2}, \quad \cancel{x=-5 \sqrt{2}}$
	如果我们用计算器将这个数字近似到最接近的十分之一，我们就会发现$x≈7.1$。
第 6 步：检查答案。在毕达哥拉斯定理中自己检查一下。
第 7 步：回答问题。	杆子应该高约一$7.1$英尺。

练习$\PageIndex{7}$

太阳从旗杆上投下阴影。旗杆的高度是其阴影长度的三倍。阴影末端与旗杆顶部之间的距离为$20$英尺。找出阴影的长度和旗杆的长度。四舍五入到最接近的十分之一。

回答: 旗杆阴影的长度约为$6.3$英尺，旗杆的高度为$18.9$英尺。

练习$\PageIndex{8}$

矩形场的对角之间的距离比该场的宽度多四个。字段的长度是其宽度的两倍。找出相反角落之间的距离。四舍五入到最接近的十分之一。

回答: 对角之间的距离约为$7.2$英尺。

从地面向上射出的弹丸的高度由二次方程建模。初始速度推动物体向上推动，$v_{0}$直到重力导致物体向下回落。

定义$\PageIndex{4}$

公式给出了以初始速度向上射向空中的物体的高度（以英尺为$t$单位）$h$$v_{0}$

$h=-16 t^{2}+v_{0} t$

我们可以使用这个公式来计算烟花达到特定高度需要多少秒。

示例$\PageIndex{5}$

烟花以初始速度$130$英尺每秒向上射击。达到$260$英尺高度需要几秒钟？四舍五入到最接近的十分之一秒。

解决方案：

表 9.5.4
第 1 步：阅读问题。
第 2 步：确定我们在寻找什么。	我们正在寻找秒数，也就是时间。
第 3 步：说出我们要找的内容。	假$t=$设秒数。
第 4 步：转换为方程式。使用公式。	$。$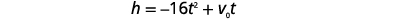
步骤 5：求解方程。我们知道速度$v_{0}$是$130$英尺每秒。高度是$260$英尺。替换这些值。	$。$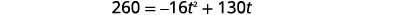
这是一个二次方程，用标准形式重写。使用二次公式求解方程。	$。$
确定的值$a, b, c$。	$。$
写下二次方程式。	$。$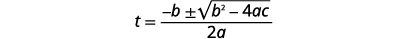
然后替换为的值$a,b,c$。	$。$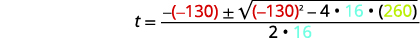
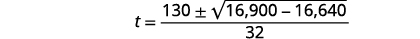
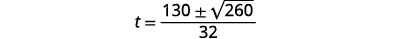
简化。	$。$ $。$ 图 9.5.26
重写以显示两个解决方案。	$。$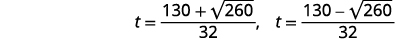
用计算器估算答案。	$。$
第 6 步：检查答案。支票留给你了。
第 7 步：回答问题。	烟花会上升然后掉下来。随着烟花的升高，它将在大约$3.6$几秒钟后到达$260$英尺。它也会在$4.6$几秒钟内向下穿过那个高度。

练习$\PageIndex{9}$

一支箭以$108$ ft/s 的初始速度从地面射向空中。使用公式$h=-16 t^{2}+v_{0} t$来确定箭何时会离地面几$180$英尺。四舍五入最接近的十分之一。

回答: $3$几秒钟后，箭将在向上移动时伸到$180$脚下，大约几秒$3.8$钟后再次向下移动。

练习$\PageIndex{10}$

一个人以$96$ ft/s 的速度向空中投球。使用公式$h=-16 t^{2}+v_{0} t$来确定球的高度何时为$48$英尺。四舍五入到最接近的十分之一。

回答: 大约一秒钟后，球将在向上的路上伸到$48$脚下，大约$.6$$5.4$几秒钟后再次向下。

我们已经使用前几章$D=rt$中的公式解决了均匀运动问题。我们使用了如下所示的表格来整理信息并引导我们得出方程式。

该图显示了包含三行四列的表的模板。第一列为空。第二列标有 “rate.á€” 第三列标有 “时间”。第四列标有 “距离”。标签写在方程中 “速率乘以时间等于距离”。第四列的底部还有一个额外的单元格。 — 图 9.5.29

该公式$D=rt$假设我们知道$r$$t$并使用它们来查找$D$。如果我们知道$D$$r$并且需要找到$t$，我们将求解方程$t$并得到公式$t=\frac{D}{r}$。

一些均匀运动问题也由二次方程建模。

示例$\PageIndex{6}$

史密斯教授刚从离他家以东$2,000$几英里处的一个会议回来。他在飞机上的往返总时间为$9$几个小时。如果飞机以每小时$450$英里的速度飞行，那么喷气流的速度是多少？

解决方案：

这是一种统一的运动情况。图表将帮助我们直观地了解情况。

第一张图显示了飞机以每小时 450 英里的速度运动，右边有一个箭头。飞机随风行驶 2000 英里，用表达式 450 加 r 表示。喷气流运动向右。往返需要 9 个小时。在图的底部，左边的箭头模拟飞机的返回运动。飞机的速度为每小时 450 英里，逆风运动速度为 2000 英里，由表情 450 “r” 建模。™ — 图 9.5.30

我们填写图表来整理信息。

我们正在寻找喷气流的速度。让$r=$喷气流的速度流过来。

当飞机随风飞行时，风会提高其速度，速度也是如此$450 + r$。

当飞机逆风飞行时，风速会降低，速度降低$450 − r$。

表 9.5.5
写下费率。在远处写字。从那以后$D=r⋅t$，我们求解 $t$并得到$t=\frac{D}{r}$。我们将距离除以每行的速率，然后将表达式放在时间列中。	$。$
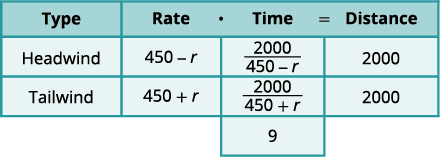我们知道时代会增加$9$ ，所以我们写下了方程式。	$\frac{2000}{450-r}+\frac{2000}{450+r}=9$
我们将两边乘以液晶屏。	$(450-r)(450+r)\left(\frac{2000}{450-r}+\frac{2000}{450+r}\right)=9(450-r)(450+r)$
简化。	$2000(450+r)+2000(450-r)=9(450-r)(450+r)$
考虑到$2,000$.	$2000(450+r+450-r)=9\left(450^{2}-r^{2}\right)$
解决。	$2000(900)=9\left(450^{2}-r^{2}\right)$
除以$9$。	$2000(100)=450^{2}-r^{2}$
简化。	$\begin{aligned}200000&=202500-r^{2} \\ -2500&=-r^{2}\\ 50&=r\end{aligned}$\ 喷气流的速度为$50$英里每小时.
查看： $50$mph 是喷气流的合理速度吗？是的。如果飞机以英里/小时的$450$速度行驶而风速为$50$英里每小时，顺风 $450+50=500 \mathrm{mph} \quad \frac{2000}{500}=4$小时逆风 $450-50=400 \mathrm{mph} \quad \frac{2000}{400}=5$小时时间增加了$9$时间，所以它会检查一下。

喷气流的速度为$50$英里每小时.

练习$\PageIndex{11}$

MaryAnne 刚带着孙子们回到东部探望回来。这次旅行离她家只有$2400$几英里远，她在飞机上的往返总时间为$10$几个小时。如果飞机以每小时$500$英里的速度飞行，那么喷气流的速度是多少？

回答: 喷气流的速度为$100$英里每小时.

练习$\PageIndex{12}$

格里刚从越野旅行中回来。这次旅行离他家只有$3000$几英里远，他在飞机上的往返总时间为$11$几个小时。如果飞机以每小时$550$英里的速度飞行，那么喷气流的速度是多少？

回答: 喷气流的速度为$50$英里每小时.

也可以通过二次方程对工作应用程序进行建模。我们将使用与使用有理方程求解它们时所用的方法相同的方法来设置它们。我们现在将使用类似的场景。

示例$\PageIndex{7}$

每周八卦杂志有一篇关于总统大选的重大报道，编辑希望该杂志尽快出版。她要求打印机额外运行一台印刷机以更快地完成打印。按 #1 比按 #2 多花$12$几个小时才能完成作业，当两台印刷机都在运行时，它们可以在$8$数小时内打印作业。每台印刷机单独打印作业需要多长时间？

解决方案：

这是一个工作问题。图表将帮助我们整理信息。

我们正在寻找每台印刷机分别需要多少小时才能完成这项工作。

表 9.5.6
$x=$输入按 #2 完成任务的小时数。输入每项作业的工时，按 #1，按 #2，以及它们何时协同工作。	$。$
由 Press #1 完成的部分加上 Press #2 完成的部分等于总完成的数量。转换为方程。	$。$
解决。	$。$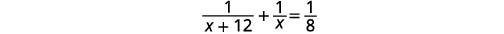
乘以液晶屏 8$x(x+12)$。	$。$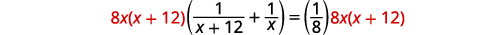
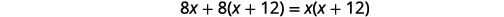
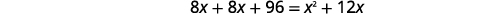
简化。	$。$ $。$ 图 9.5.37 $。$ 图 9.5.38
解决。	$。$ $。$ 图 9.5.40 $。$ 图 9.5.41
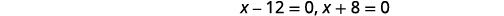
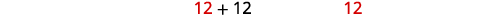
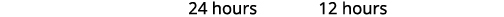
由于负时数的概念没有意义，因此我们使用这些值$x=12$。	$。$ $。$ 图 9.5.43
写下我们的句子答案。	按 #1 需要$24$几个小时，而按 #2 则需要$12$几个小时才能单独完成这项工作。

练习$\PageIndex{13}$

每周新闻杂志有一篇名为 “年度人物” 的重大报道，编辑希望该杂志尽快出版。她要求打印机额外运行一台印刷机以更快地完成打印。按 #1 比按 #2 多花$6$几个小时才能完成作业，当两台印刷机都在运行时，它们可以在$4$数小时内打印作业。每台印刷机单独打印作业需要多长时间？

回答: 按 #1 需要$12$几个小时，而按 #2 则需要$6$几个小时才能单独完成这项工作。

练习$\PageIndex{14}$

Erlinda 正在开派对，想把她的热水浴缸装满。如果她只使用红色软管，则比只使用绿色软管要多花$3$几个小时。如果她同时使用两根软管，热水浴缸将在$2$数小时内填满。每根软管填满热水浴缸需要多长时间？

回答: 红色软管需要$6$几个小时，绿色软管单独需要$3$几个小时。

访问这些在线资源，获取有关求解二次方程建模应用程序的更多指导和练习。

关键概念

求解二次方程的方法
- 保理
- 平方根属性
- 完成方块
- 二次方程式
如何使用问题解决策略。
1. 阅读问题。确保所有文字和想法都被理解。
2. 确定我们在寻找什么。
3. 说出我们要找的东西。选择一个变量来表示该数量。
4. 翻译成方程式。用一句话用所有重要信息重述问题可能会有所帮助。然后，将英语句子翻译成代数方程。
5. 使用良好的代数技巧求@@ 解方程。
6. 检查问题中的答案并确保答案合理。
7. 用完整的句子@@ 回答问题。
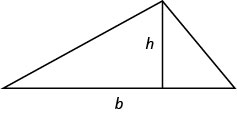
三角形的面积
- 对于基数和高度的三角形$h$，面积由公式给出$A=\frac{1}{2}bh$。$b$$A$

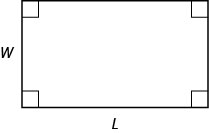
矩形的面积
- 对于长度$L$、宽度均为的矩形$A$，面积由公式给出$A=LW$。$W$

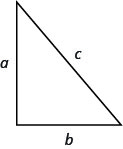
毕达哥拉斯定理
- 在任何直角三角形中，其中$a$和$b$是腿的长度，$c$是斜边的长度$a^{2}+b^{2}=c^{2}$。

射弹运动
- 公式给出了以初始速度向上射向空中的物体的高度（以英尺为单位）$v_{0}$，在$t$秒后由公式给出$h=-16 t^{2}+v_{0} t$。$h$

第 1 步：阅读问题。画一张照片。	$。$
第 2 步：确定我们在寻找什么。	我们正在寻找底座和高度。
第 3 步：说出我们要找的内容。	假\(h=\)设三角形的高度。 \(2h+4=\)三角形的底部。
第 4 步：转换为方程式。我们知道这个地区。写出三角形面积的公式。	\(A=\frac{1}{2} b h\)
步骤 5：求解方程。在值中替换。	\(120=\frac{1}{2}(2 h+4) h\)
分发。	\(120=h^{2}+2 h\)
这是一个二次方程，用标准形式重写。	\(h^{2}+2 h-120=0\)
因子。	\((h-10)(h+12)=0\)
使用 “零积分” 属性。	\(h-10=0 \quad h+12=0\)
简化。	\(h=10, \quad \cancel{h=-12}\)
因为\(h\)是窗口的高度，所以值是\(h=-12\)没有意义的。
三角形的高度\(h=10\)。
三角形的底部\(2h+4\)。 \(2 \cdot 10+4\) \(24\)
第 6 步：检查答案。有高度\(10\)和底部的三角形\(24\)有面积\(120\)吗？是的。
第 7 步：回答问题。	三角窗的高度为\(10\)英尺，底部为\(24\)英尺。

写下费率。在远处写字。从那以后\(D=r⋅t\)，我们求解 \(t\)并得到\(t=\frac{D}{r}\)。我们将距离除以每行的速率，然后将表达式放在时间列中。	$。$
我们知道时代会增加\(9\) ，所以我们写下了方程式。	\(\frac{2000}{450-r}+\frac{2000}{450+r}=9\)
我们将两边乘以液晶屏。	\((450-r)(450+r)\left(\frac{2000}{450-r}+\frac{2000}{450+r}\right)=9(450-r)(450+r)\)
简化。	\(2000(450+r)+2000(450-r)=9(450-r)(450+r)\)
考虑到\(2,000\).	\(2000(450+r+450-r)=9\left(450^{2}-r^{2}\right)\)
解决。	\(2000(900)=9\left(450^{2}-r^{2}\right)\)
除以\(9\)。	\(2000(100)=450^{2}-r^{2}\)
简化。	\(\begin{aligned}200000&=202500-r^{2} \\ -2500&=-r^{2}\\ 50&=r\end{aligned}\)\ 喷气流的速度为\(50\)英里每小时.
查看： \(50\)mph 是喷气流的合理速度吗？是的。如果飞机以英里/小时的\(450\)速度行驶而风速为\(50\)英里每小时，顺风 \(450+50=500 \mathrm{mph} \quad \frac{2000}{500}=4\)小时逆风 \(450-50=400 \mathrm{mph} \quad \frac{2000}{400}=5\)小时时间增加了\(9\)时间，所以它会检查一下。

示例\(\PageIndex{1}\)

练习\(\PageIndex{1}\)

练习\(\PageIndex{2}\)

定义\(\PageIndex{1}\)

示例\(\PageIndex{2}\)

练习\(\PageIndex{3}\)

练习\(\PageIndex{4}\)

定义\(\PageIndex{2}\)

示例\(\PageIndex{3}\)

练习\(\PageIndex{5}\)

练习\(\PageIndex{6}\)

定义\(\PageIndex{3}\)

示例\(\PageIndex{4}\)

练习\(\PageIndex{7}\)

练习\(\PageIndex{8}\)

定义\(\PageIndex{4}\)

示例\(\PageIndex{5}\)

练习\(\PageIndex{9}\)

练习\(\PageIndex{10}\)

示例\(\PageIndex{6}\)

练习\(\PageIndex{11}\)

练习\(\PageIndex{12}\)

示例\(\PageIndex{7}\)

练习\(\PageIndex{13}\)

练习\(\PageIndex{14}\)

\(x=\)输入按 #2 完成任务的小时数。输入每项作业的工时，按 #1，按 #2，以及它们何时协同工作。	$。$
由 Press #1 完成的部分加上 Press #2 完成的部分等于总完成的数量。转换为方程。	$。$
解决。	$。$
乘以液晶屏 8\(x(x+12)\)。	$。$
简化。	$。$ $。$ 图 9.5.37 $。$ 图 9.5.38
解决。	$。$ $。$ 图 9.5.40 $。$ 图 9.5.41
由于负时数的概念没有意义，因此我们使用这些值\(x=12\)。	$。$ $。$ 图 9.5.43
写下我们的句子答案。	按 #1 需要\(24\)几个小时，而按 #2 则需要\(12\)几个小时才能单独完成这项工作。