9.5:求解二次形式的二次方程
- Page ID
- 204090
在本节结束时,您将能够:
- 以二次形式求解方程
... 参加这个准备测验。
- 替代因子:\(y^{4}-y^{2}-20\).
- 替代因子:\((y-4)^{2}+8(y-4)+15\).
- 简化
- \(x^{\frac{1}{2}} \cdot x^{\frac{1}{4}}\)
- \(\left(x^{\frac{1}{3}}\right)^{2}\)
- \(\left(x^{-1}\right)^{2}\)
以二次形式求解方程
有时候,当我们考虑三项式时,三项式似乎不是这种\(ax^{2}+bx+c\)形式。 因此,我们考虑了替代因素,使之符合\(ax^{2}+bx+c\)形式。 我们使用了标准\(u\)作为替代。
为了分解表达式\(x^{4}-4 x^{2}-5\),我们注意到中间项的可变部分是\(x^{2}\)\(x^{4}\),其平方是第一个项的可变部分。 (我们知道\(\left(x^{2}\right)^{2}=x^{4}\)。) 因此,我们放手\(u=x^{2}\)并考虑了因素。
| \(x^{4}-4 x^{2}-5\) | |
| \(\left(\color{red}x^2 \color{black} \right)^{2}-4\left( \color{red}x^{2} \color{black}\right)-5\) | |
| 让我们\(u=x^{2}\)替换。 | \(\color{red}u \color{black}^{2}-4 \color{red}u \color{black}-5\) |
| 将三项式分解为因子。 | \((u+1)(u-5)\) |
| 替换\(u\)为\(x^{2}\)。 | \(\left( \color{red}x^{2} \color{black} + 1\right)\left( \color{red}x^2 \color{black}-5\right)\) |
同样,有时方程不是这种\(ax^{2}+bx+c=0\)形式,但看起来很像二次方程。 然后,我们通常可以进行深思熟虑的替换,使我们能够使其符合\(ax^{2}+bx+c=0\)形式。 如果我们能使它符合形式,那么我们就可以使用所有的方法来求解二次方程。
请注意,在二次方程中\(ax^{2}+bx+c=0\),中间项有一个变量\(x\)\(x^{2}\),其平方是第一个项的可变部分。 当你尝试寻找替代品时,请寻找这种关系。
同样,我们将使用标准\(u\)进行替换,将方程置于二次形式。 如果替换给我们一个形式的方程\(ax^{2}+bx+c=0\),我们就说原始方程是二次形式。
下一个示例显示了求解二次形式方程的步骤。
解决:\(6 x^{4}-7 x^{2}+2=0\)
解决方案:
| 步骤 1:确定一个替代方案,它将使方程呈二次形式。 | 从那以后\(\left(x^{2}\right)^{2}=x^{4}\),我们放手\(u=x^{2}\)了。 | \(6 x^{4}-7 x^{2}+2=0\) |
| 第 2 步:使用替换重写方程,使其成为二次形式。 |
重写为替换做准备。 替代\(u=x^{2}\)。 |
\(\begin{aligned}6\color{black}{\left(\color{red}{x^{2}}\right)}^{2}-7\color{red}{ x^{2}}\color{black}{+}2&=0 \\ \color{black}{6 \color{red}{u}^{2}}-7 \color{red}{u}\color{black}{+}2&=0\end{aligned}\) |
| 步骤 3:求解二次方程\(u\)。 |
我们可以通过保理来解决。 使用 “零积分” 属性。 |
\(\begin{aligned}(2 u-1)(3 u-2) &=0 \\ 2 u-1=0, 3 u-2&=0 \\ 2 u =1,3 u&=2 \\ u =\frac{1}{2} u&=\frac{2}{3} \end{aligned}\) |
| 步骤 4:使用替换将原始变量替换回结果中。 | 替换\(u\)为\(x^{2}\)。 | \(x^{2}=\frac{1}{2} \quad x^{2}=\frac{2}{3}\) |
| 步骤 5:求解原始变量。 | 使用平方根属性求解。\(x\) |
\(\begin{array}{ll}{x=\pm \sqrt{\frac{1}{2}}} & {x=\pm \sqrt{\frac{2}{3}}} \\ {x=\pm \frac{\sqrt{2}}{2}} & {x=\pm \frac{\sqrt{6}}{3}}\end{array}\) 有四种解决方案。 \(\begin{array}{ll}{x=\frac{\sqrt{2}}{2}} & {x=\frac{\sqrt{6}}{3}} \\ {x=-\frac{\sqrt{2}}{2}} & {x=-\frac{\sqrt{6}}{3}}\end{array}\) |
| 第 6 步:检查解决方案。 | 检查所有四个解决方案。 我们将在此处显示一张支票。 |
\(\begin{aligned}x&=\frac{\sqrt{2}}{2} \\ 6 x^{4}-7 x^{2}+2&=0 \\ 6\left(\frac{\sqrt{2}}{2}\right)^{4}-7\left(\frac{\sqrt{2}}{2}\right)^{2}+2 &\stackrel{?}{=} 0\\ 6\left(\frac{4}{16} \right)-7\left(\frac{2}{4} \right)^{2}+2&\stackrel{?}{=}0 \\ \frac{3}{2}-\frac{7}{2}+\frac{4}{2}&\stackrel{?}{=}0 \\ 0&=0 \end{aligned}\) 我们把其他支票留给你! |
解决:\(x^{4}-6 x^{2}+8=0\)。
- 回答
-
\(x=\sqrt{2}, x=-\sqrt{2}, x=2, x=-2\)
解决:\(x^{4}-11 x^{2}+28=0\)。
- 回答
-
\(x=\sqrt{7}, x=-\sqrt{7}, x=2, x=-2\)
我们总结了求解二次形式方程的步骤。
- 找出一个将方程变为二次形式的替换。
- 使用替换重写方程,使其成为二次形式。
- 求解二次方程\(u\)。
- 使用替换将原始变量替换回结果中。
- 求解原始变量。
- 检查解决方案。
在下一个示例中,中间项中的二项式\((x-2)\)是第一个项的平方。 如果我们让\(u=x-2\)和替换,我们的三项式就会\(a x^{2}+b x+c\)形成形式。
解决:\((x-2)^{2}+7(x-2)+12=0\)。
解决方案:
| \((x-2)^{2}+7(x-2)+12=0\) | |
| 为替补做准备。 | \(\color{red}(x-2)\color{black}^{2}+7\color{red}(x-2) \color{black} +12=0\) |
| 让我们\(u=x-2\)替换。 | \(\color{red}u^{\color{black}2} \color{black}+ 7 \color{red}u \color{black}+12=0\) |
| 通过分解求解。 |
\((u+3)(u+4)=0\) \ (\ begin {聚集} |
|
替换\(u\)为\(x-2\)。 |
\(x-2=-3, \quad x-2=-4\) |
|
求解\(x\)。 |
\(x=-1, \quad x=-2\) |
|
查看: 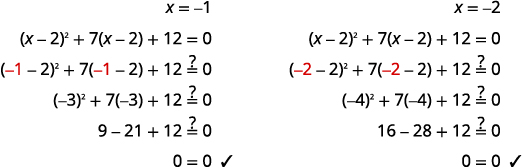
|
解决:\((x-5)^{2}+6(x-5)+8=0\)。
- 回答
-
\(x=3, x=1\)
解决:\((y-4)^{2}+8(y-4)+15=0\)。
- 回答
-
\(y=-1, y=1\)
在下一个示例中,我们注意到了这一点\((\sqrt{x})^{2}=x\)。 另外,请记住,当我们对方程的两边进行平方时,我们可能会引入无关的根。 一定要检查你的答案!
解决:\(x-3 \sqrt{x}+2=0\)。
解决方案:
中间学期的,是第一个学期的平方\((\sqrt{x})^{2}=x\)。\(\sqrt{x}\) 如果我们让\(u=\sqrt{x}\)和替换,我们的三项式就会\(a x^{2}+b x+c=0\)形成形式。
| \(x-3 \sqrt{x}+2=0\) | |
| 重写三项式为替换做准备。 | 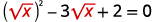 |
| 让我们\(u=\sqrt{x}\)替换。 | 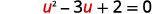 |
| 通过分解求解。 |
\((u-2)(u-1)=0\) \(u-2=0, \quad u-1=0\) |
| 替换\(u\)为\(\sqrt{x}\)。 |
\(\sqrt{x}=2, \quad \sqrt{x}=1\) |
| 求解\(x\),将两边平方。 | \(x=4, \quad x=1\) |
|
查看: 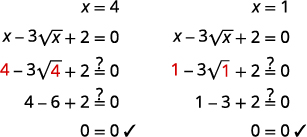 |
解决:\(x-7 \sqrt{x}+12=0\)。
- 回答
-
\(x=9, x=16\)
解决:\(x-6 \sqrt{x}+8=0\)。
- 回答
-
\(x=4, x=16\)
替换有理指数也可以帮助我们求解二次形式的方程。 在开始下一个示例时,请考虑指数的属性。
解决:\(x^{\frac{2}{3}}-2 x^{\frac{1}{3}}-24=0\)。
解决方案:
中间\(x^{\frac{1}{3}}\)项是第一个学期的平方\(\left(x^{\frac{1}{3}}\right)^{2}=x^{\frac{2}{3}}\)。 如果我们让\(u=x^{\frac{1}{3}}\)和替换,我们的三项式就会\(a x^{2}+b x+c=0\)形成形式。
| \(x^{\frac{2}{3}}-2 x^{\frac{1}{3}}-24=0\) | |
| 重写三项式为替换做准备。 | 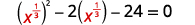 |
| 让\(u=x^{\frac{1}{3}}\) |  |
| 通过分解求解。 |
\((u-6)(u+4)=0\) \(u-6=0, \quad u+4=0\) \(u=6, \quad u=-4\) |
| 替换\(u\)为\(x^{\frac{1}{3}}\)。 |
\(x^{\frac{1}{3}}=6, \quad x^{\frac{1}{3}}=-4\) |
| \(x\)通过将两边都立方来求解。 |
\(\left(x^{\frac{1}{3}}\right)^{3}=(6)^{3}, \quad\left(x^{\frac{1}{3}}\right)^{3}=(-4)^{3}\) \(x=216, \quad x=-64\) |
|
查看: 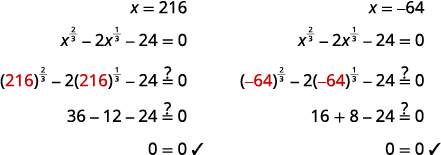
|
解决:\(x^{\frac{2}{3}}-5 x^{\frac{1}{3}}-14=0\)。
- 回答
-
\(x=-8, x=343\)
解决:\(x^{\frac{1}{2}}+8 x^{\frac{1}{4}}+15=0\)。
- 回答
-
\(x=81, x=625\)
在下一个示例中,我们需要记住负指数的定义以及指数的属性。
解决:\(3 x^{-2}-7 x^{-1}+2=0\)。
解决方案:
中间\(x^{−1}\)项是第一个学期的平方\(\left(x^{-1}\right)^{2}=x^{-2}\)。 如果我们让\(u=x^{−1}\)和替换,我们的三项式就会\(a x^{2}+b x+c=0\)形成形式。
| \(3 x^{-2}-7 x^{-1}+2=0\) | |
| 重写三项式为替换做准备。 | 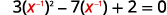 |
| 让我们\(u=x^{-1}\)替换。 | 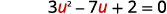 |
| 通过分解求解。 | \((3 u-1)(u-2)=0\) |
| \(3 u-1=0, \quad u-2=0\) | |
| \(u=\frac{1}{3}, \quad u=2\) | |
| 替换\(u\)为\(x^{-1}\)。 | \(x^{-1}=\frac{1}{3}, \quad x^{-1}=2\) |
| \(x\)通过取自起的倒数求解\(x^{-1}=\frac{1}{x}\)。 | \(x=3, \quad x=\frac{1}{2}\) |
|
查看: 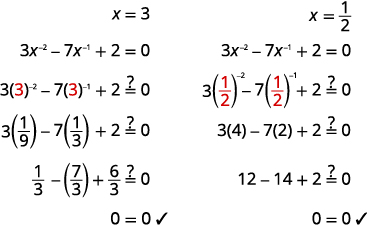
|
解决:\(8 x^{-2}-10 x^{-1}+3=0\)。
- 回答
-
\(x=\frac{4}{3}, x=2\)
解决:\(6 x^{-2}-23 x^{-1}+20=0\)。
- 回答
-
\(x=\frac{2}{5}, x=\frac{3}{4}\)
观看此在线视频,获取有关求解二次方程的更多指导和练习:https://www.youtube.com/watch?v=7X-CZMbpxuw
关键概念
- 如何以二次形式求解方程。
- 找出一个将方程变为二次形式的替换。
- 使用替换重写方程,使其成为二次形式。
- 求解二次方程\(u\)。
- 使用替换将原始变量替换回结果中。
- 求解原始变量。
- 检查解决方案。


