Skip to main content
Global

9.4E：练习

  1. Last updated
  2. Save as PDF
  • Page ID
    204124

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    练习成就完美

    练习 1-32：使用二次公式求解二次方程

    在以下练习中，使用二次公式求解。

    1。 \(4 m^{2}+m-3=0\)

    2。 \(4 n^{2}-9 n+5=0\)

    3。 \(2 p^{2}-7 p+3=0\)

    4。 \(3 q^{2}+8 q-3=0\)

    5。 \(p^{2}+7 p+12=0\)

    6。 \(q^{2}+3 q-18=0\)

    7。 \(r^{2}-8 r=33\)

    8。 \(t^{2}+13 t=-40\)

    9。 \(3 u^{2}+7 u-2=0\)

    10。 \(2 p^{2}+8 p+5=0\)

    11。 \(2 a^{2}-6 a+3=0\)

    12。 \(5 b^{2}+2 b-4=0\)

    13。 \(x^{2}+8 x-4=0\)

    14。 \(y^{2}+4 y-4=0\)

    15。 \(3 y^{2}+5 y-2=0\)

    16。 \(6 x^{2}+2 x-20=0\)

    17。 \(2 x^{2}+3 x+3=0\)

    18。 \(2 x^{2}-x+1=0\)

    19。 \(8 x^{2}-6 x+2=0\)

    20。 \(8 x^{2}-4 x+1=0\)

    21。 \((v+1)(v-5)-4=0\)

    22。 \((x+1)(x-3)=2\)

    23。 \((y+4)(y-7)=18\)

    24。 \((x+2)(x+6)=21\)

    25。 \(\dfrac{1}{4} m^{2}+\dfrac{1}{12} m=\dfrac{1}{3}\)

    26。 \(\dfrac{1}{3} n^{2}+n=-\dfrac{1}{2}\)

    27。 \(\dfrac{3}{4} b^{2}+\dfrac{1}{2} b=\dfrac{3}{8}\)

    28。 \(\dfrac{1}{9} c^{2}+\dfrac{2}{3} c=3\)

    29。 \(16 c^{2}+24 c+9=0\)

    30。 \(25 d^{2}-60 d+36=0\)

    31。 \(25 q^{2}+30 q+9=0\)

    32。 \(16 y^{2}+8 y+1=0\)

    回答

    1。 \(m=-1, m=\dfrac{3}{4}\)

    3。 \(p=\dfrac{1}{3}, p=2\)

    5。 \(p=-4, p=-3\)

    7。 \(r=-3, r=11\)

    9。 \(u=\dfrac{-7 \pm \sqrt{73}}{6}\)

    11。 \(a=\dfrac{3 \pm \sqrt{3}}{2}\)

    13。 \(x=-4 \pm 2 \sqrt{5}\)

    15。 \(y=-\dfrac{2}{3}, y=-1\)

    17。 \(x=-\dfrac{3}{4} \pm \dfrac{\sqrt{15}}{4} i\)

    19。 \(x=\dfrac{3}{8} \pm \dfrac{\sqrt{7}}{8} i\)

    21。 \(v=2 \pm 2 \sqrt{2}\)

    23。 \(y=-4, y=7\)

    25。 \(m=1, m=\dfrac{-4}{3}\)

    27。 \(b=\dfrac{-2 \pm \sqrt{22}}{6}\)

    29。 \(c=-\dfrac{3}{4}\)

    31。 \(q=-\dfrac{3}{5}\)

    练习 33-36 使用判别法预测二次方程的实解数

    在以下练习中，确定每个二次方程的实解数。

      1. \(4 x^{2}-5 x+16=0\)
      2. \(36 y^{2}+36 y+9=0\)
      3. \(6 m^{2}+3 m-5=0\)
      1. \(9 v^{2}-15 v+25=0\)
      2. \(100 w^{2}+60 w+9=0\)
      3. \(5 c^{2}+7 c-10=0\)
      1. \(r^{2}+12 r+36=0\)
      2. \(8 t^{2}-11 t+5=0\)
      3. \(3 v^{2}-5 v-1=0\)
      1. \(25 p^{2}+10 p+1=0\)
      2. \(7 q^{2}-3 q-6=0\)
      3. \(7 y^{2}+2 y+8=0\)
    回答

    33. a. 没有真正的解决办法 b.\(1\) c.\(2\)

    35. a.\(1\) b. 没有真正的解决方案 c.\(2\)

    练习 37-40：确定用于求解二次方程的最合适方法

    在以下练习中，确定用于求解每个二次方程的最合适的方法（因子分解、平方根或二次公式）。 不要解决。

      1. \(x^{2}-5 x-24=0\)
      2. \((y+5)^{2}=12\)
      3. \(14 m^{2}+3 m=11\)
      1. \((8 v+3)^{2}=81\)
      2. \(w^{2}-9 w-22=0\)
      3. \(4 n^{2}-10=6\)
      1. \(6 a^{2}+14=20\)
      2. \(\left(x-\dfrac{1}{4}\right)^{2}=\dfrac{5}{16}\)
      3. \(y^{2}-2 y=8\)
      1. \(8 b^{2}+15 b=4\)
      2. \(\dfrac{5}{9} v^{2}-\dfrac{2}{3} v=1\)
      3. \(\left(w+\dfrac{4}{3}\right)^{2}=\dfrac{2}{9}\)
    回答

    37. a. 因子 b. 平方根 c. 二次公式

    39. a. 二次公式 b. 平方根 c. 因子

    练习 41-42：写作练习
    1. 求解方程\(x^{2}+10 x=120\)
      1. 通过完成正方形
      2. 使用二次公式
      3. 你更喜欢哪种方法？ 为什么？
    2. 求解方程\(12 y^{2}+23 y=24\)
      1. 通过完成正方形
      2. 使用二次公式
      3. 你更喜欢哪种方法？ 为什么？
    回答

    41。 答案会有所不同

    自检

    a. 完成练习后，使用此清单评估您对本节目标的掌握程度。

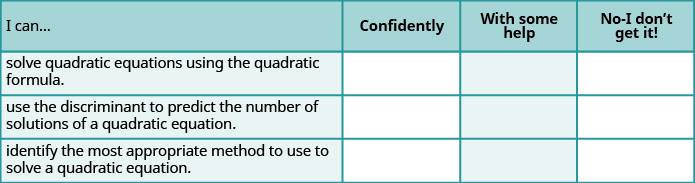
    此表提供了一份清单，用于评估对本节目标的掌握程度。 选择你将如何回应这个说法 “我能用二次公式求解二次方程。” 自信地，“在一些帮助下，” 或 “不，我不明白。” 选择你将如何回应这个陈述 “我可以用判别来预测二次方程的解数™equation.ဠ“自信地，” 有了一些帮助，“或者 “不，我不明白。” 选择你将如何回应这句话 “我能找到最合适的求解二次方程的方法。” ¿€™ 不明白。¿€™
    图 9.3.87

    b. 关于你对本部分的掌握程度，这份清单告诉了你什么？ 你会采取哪些措施来改进？