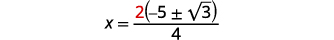9.4:使用二次公式求解二次方程
- Page ID
- 204112
在本节结束时,您将能够:
- 使用二次公式求解二次方程
- 使用判别函数预测二次方程解的数量和类型
- 确定用于求解二次方程的最合适方法
在开始之前,请参加这个准备测验。
- 评估\(b^{2}-4 a b\)何时\(a=3\)和\(b=−2\)。
- 简化\(\sqrt{108}\)。
- 简化\(\sqrt{50}\)。
使用二次公式求解二次方程
当我们在最后一节中通过完成正方形求解二次方程时,我们每次都采取相同的步骤。 在练习集结束时,你可能想知道 “没有更简单的方法可以做到这一点吗?” 答案是 “是”。 数学家一遍又一遍地做事时会寻找模式,以便更轻松地完成工作。 在本节中,我们将推导并使用公式来找到二次方程的解。
我们已经看到了如何 “一般地” 求解特定变量的公式,因此我们只做一次代数步骤,然后使用新公式来找出特定变量的值。 现在,我们将通过使用二次方程的一般形式完成正方程的步骤,以求解二次方程\(x\)。
我们从二次方程的标准形式开始,然后\(x\)通过完成方程来求解。
| \(ax^2 + bx + c = 0, \quad a \ne 0\) | |
| 隔离一侧的变量项。 | \(ax^2 + bx \quad = -c\) |
| 将系数除以\(1\),使系数\(x^{2}\)等于\(a\)。 | \(\dfrac{ax^2}{a} + \dfrac{b}{a}x \quad = -\dfrac{c}{a}\) |
| 简化。 | \(x^2+ \dfrac{b}{a}x \quad = -\dfrac{c}{a}\) |
| 要完成正方形,请找到\(\left(\dfrac{1}{2} \cdot \dfrac{b}{a}\right)^{2}\)并将其添加到方程的两边。 | |
| \(\left(\dfrac{1}{2} \dfrac{b}{a}\right)^{2}=\dfrac{b^{2}}{4 a^{2}}\) | \(x^2 + \dfrac{b}{a}x +{\color{red}{\dfrac{b^2}{4a^2}}}{\color{black}{ = -\dfrac{c}{a}\,+\,}}{\color{red}{\dfrac{b^2}{4a^2}}}\) |
| 左边是一个完美的正方形,将其考虑在内。 | \(\left( x + \dfrac{b}{2a}\right)^2 = -\dfrac{c}{a}+\dfrac{b^2}{4a^2}\) |
| 找到右侧的公分母,用公分母写出等效分数。 | \(\left( x + \dfrac{b}{2a}\right)^2 =\dfrac{b^2}{4a^2}-\dfrac{c\cdot\color{red}{4a}}{a\cdot\color{red}{4a}}\) |
| 简化。 | \(\left( x + \dfrac{b}{2a}\right)^2 =\dfrac{b^2}{4a^2}-\dfrac{4ac}{4a^2}\) |
| 合并为一个分数。 | \(\left( x + \dfrac{b}{2a}\right)^2 =\dfrac{b^2-4ac}{4a^2}\) |
| 使用平方根属性。 | \(x + \dfrac{b}{2a}= \pm\sqrt{\dfrac{b^2-4ac}{4a^2}}\) |
| 简化激进。 | \(x + \dfrac{b}{2a}= \pm\dfrac{\sqrt{b^2-4ac}}{2a}\) |
| 加\(-\dfrac{b}{2a}\)到等式的两边。 | \(x = -\dfrac{b}{2a} \pm\dfrac{\sqrt{b^2-4ac}}{2a}\) |
| 合并右侧的术语。 | \(x = \dfrac{-b\pm\sqrt{b^2-4ac}}{2a}\) |
最后一个方程称为 “二次公式”。
以下形式的二次方程的解\(a x^{2}+b x+c=0\),其中\(a≠0\)由公式给出:
\[x=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a} \label{quad}\]
要使用二次公式,我们将标准形式\(c\)中的和值替换为公式右侧的表达式。\(a,b\) 然后我们简化表达式。 结果是二次方程的一对解。
注意二次公式(方程\ ref {quad})是一个方程。 确保使用方程的两边。
使用二次公式求解:\(2 x^{2}+9 x-5=0\).
解决方案:
| 步骤 1:以标准形式写出二次方程。 确定\(a,b,c\)值。 | 这个方程是标准形式。 | \(\begin{aligned} \color{red}{a x^{2}+b x+c =0} \\ 2 x^{2}+9 x-5 =0 \\ a=2, b =9, c=-5 \end{aligned}\) |
| 第 2 步:写出二次方程式。 然后替换为的值\(a,b,c\)。 | 替换为\(a=2, b=9, c=-5\) | \(x=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\) \(x=\dfrac{-9 \pm \sqrt{9^{2}-4 \cdot 2 \cdot(-5)}}{2 \cdot 2}\) |
| 步骤 3:简化分数并求解\(x\)。 | \(\begin{array}{l}{x=\dfrac{-9 \pm \sqrt{81-(-40)}}{4}} \\ {x=\dfrac{-9 \pm \sqrt{121}}{4}} \\ {x=\dfrac{-9 \pm 11}{4}} \\ {x=\dfrac{-9+11}{4}}\quad x=\dfrac{-9-11}{4} \\ {x=\dfrac{2}{4} \quad \quad\:\:\: x=\dfrac{-20}{4}}\\ {x=\dfrac{1}{2} \quad\quad\:\:\: x=-5}\end{array}\) | |
| 第 4 步:检查解决方案。 | 将每个答案放在原始方程式中进行检查。 替换\(x=\color{red}{\dfrac{1}{2}}\)和\(x=\color{red}{-5}\). |
\(\begin{aligned}2 x^{2}+9 x-5&=0 \\ 2\color{black}{\left(\color{red}{\dfrac{1}{2}}\right)}^{2}+9 \cdot \color{red}{\dfrac{1}{2}}\color{black}{-}5 &\stackrel{?}{=} 0 \\ 2\cdot\dfrac{1}{4}+0\cdot\dfrac{1}{2}-5&\stackrel{?}{=}0 \\ 2\cdot\dfrac{1}{4}+9\cdot\dfrac{1}{2}-5&\stackrel{?}{=}0 \\ \dfrac{1}{2}+\dfrac{9}{2}-5&\stackrel{?}{=}0 \\ \dfrac{10}{2}-5&\stackrel{?}{=}0 \\5-5&\stackrel{?}{=}0\\0&=0\end{aligned}\) \(\begin{array}{r}{2 x^{2}+9 x-5=0} \\ {2(\color{red}{-5}\color{black}{)}^{2}+9(\color{red}{-5}\color{black}{)}-5\stackrel{?}{=}0} \\ {2 \cdot 25-45-5\stackrel{?}{=}0} \\ {50-45-5\stackrel{?}{=}0} \\ {0=0}\end{array}\) |
使用二次公式求解:\(3 y^{2}-5 y+2=0\).
- 回答
-
\(y=1, y=\dfrac{2}{3}\)
使用二次公式求解:\(4 z^{2}+2 z-6=0\).
- 回答
-
\(z=1, z=-\dfrac{3}{2}\)
- 以标准形式写下二次方程\(a x^{2}+b x+c=0\)。 确定\(a,b\)、和的值\(c\)。
- 写下二次方程式。 然后用\(a,b\)、和的值替换\(c\)。
- 简化。
- 检查解决方案。
如果你在写每个问题时说出这个公式,你很快就会记住它! 请记住,二次公式是一个方程。 请务必以 “\(x=\)” 开头。
使用二次公式求解:\(x^{2}-6 x=-5\).
解决方案:
|
\(x^{2}-6 x=-5\) |
|
| 通过将两边相加,以标准形式写\(5\)出方程。 |
\(x^{2}-6 x+5=0\) |
| 这个方程现在是标准形式。 |
\({\color{red}{\small{ax^2+bx + c} = \small{0}}}\) |
| 识别\(\color{cyan}a\)、\(\color{red}b\)、的值\(\color{limegreen}c\)。 | \({\color{cyan}a=1}\),\({\color{red}b=-6}\),\({\color{limegreen}c=5}\) |
| 写下二次方程式。 |
\(x=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\) |
| 然后替换为的值\(a, b, c\)。 |
\(x=\dfrac{-\color{red} (-6 ) \color{black} \pm \sqrt{\color{red}(-6) \color{black}^{2}-4 \cdot \color{cyan}1 \color{black} \cdot ( \color{limegreen}5 \color{black})}}{2 \cdot \color{cyan} 1} \) |
| 简化。 |
\(x=\dfrac{6 \pm \sqrt{36-20}}{2}\) \(x=\dfrac{6 \pm \sqrt{16}}{2}\) \(x=\dfrac{6 \pm 4}{2}\) |
| 重写以显示两个解决方案。 |
\(x=\frac{6+4}{2}, \quad x=\frac{6-4}{2}\) |
| 简化。 |
\(x=\frac{10}{2}, \quad x=\frac{2}{2}\) |
| \(x=5, \quad x=1\) | |
|
查看: 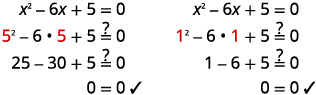 |
使用二次公式求解:\(a^{2}-2 a=15\).
- 回答
-
\(a=-3, a=5\)
使用二次公式求解:\(b^{2}+24=-10 b\).
- 回答
-
\(b=-6, b=-4\)
当我们使用平方根属性求解二次方程时,我们有时会得到含有激进的答案。 使用二次方程式时也可能发生这种情况。 如果我们以激进作为解决方案,则最终答案必须采用简化形式的激进分子。
使用二次公式求解:\(2 x^{2}+10 x+11=0\).
解决方案:
 |
|
| 这个方程是标准形式。 |  |
| 确定\(a,b\)和的值\(c\)。 |  |
| 写下二次方程式。 |
\(x=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\) |
| 然后用\(a, b\)、和的值替换\(c\)。 | 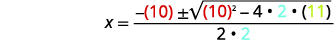 |
| 简化。 |
\(x=\dfrac{-10 \pm \sqrt{100-88}}{4}\) |
|
\(x=\dfrac{-10 \pm \sqrt{12}}{4}\) |
|
| 简化激进。 |
\(x=\dfrac{-10 \pm 2 \sqrt{3}}{4}\) |
| 分解出分子中的公因子。 |
\(x=\dfrac{\color{red}{2}(-5 \pm \sqrt{3})}{4}\) |
| 移除常见因素。 |
\(x=\dfrac{-5 \pm \sqrt{3}}{2}\) |
| 重写以显示两个解决方案。 |
\(x=\dfrac{-5+\sqrt{3}}{2}, \quad x=\dfrac{-5-\sqrt{3}}{2}\) |
|
查看: 我们把支票留给你! |
使用二次公式求解:\(3 m^{2}+12 m+7=0\).
- 回答
-
\(m=\dfrac{-6+\sqrt{15}}{3}, m=\dfrac{-6-\sqrt{15}}{3}\)
使用二次公式求解:\(5 n^{2}+4 n-4=0\).
- 回答
-
\(n=\dfrac{-2+2 \sqrt{6}}{5}, n=\dfrac{-2-2 \sqrt{6}}{5}\)
当我们将二次方程替换\(a, b\)\(c\)为二次公式并且基数为负时,二次方程将具有虚数或复数解。 我们将在下一个示例中看到这一点。
使用二次公式求解:\(3 p^{2}+2 p+9=0\).
解决方案:
 |
|
| 这个方程是标准形式。 |  |
| 确定的值\(a,b,c\)。 |  |
| 写下二次方程式。 | 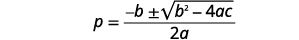 |
| 然后替换为的值\(a,b,c\)。 | 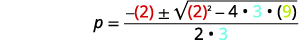 |
| 简化。 | 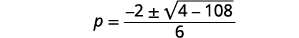 |
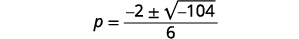 |
|
| 使用复数简化部首。 | 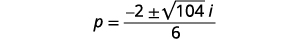 |
| 简化激进。 | 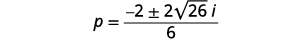 |
| 将分子中的公因子分解。 | 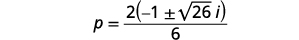 |
| 移除常见因素。 | 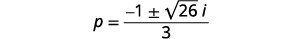 |
| 以标准\(a+bi\)形式重写。 | 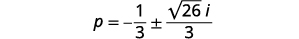 |
| 写成两个解决方案。 | 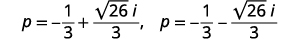 |
使用二次公式求解:\(4 a^{2}-2 a+8=0\).
- 回答
-
\(a=\dfrac{1}{4}+\dfrac{\sqrt{31}}{4} i, \quad a=\dfrac{1}{4}-\dfrac{\sqrt{31}}{4} i\)
使用二次公式求解:\(5 b^{2}+2 b+4=0\).
- 回答
-
\(b=-\dfrac{1}{5}+\dfrac{\sqrt{19}}{5} i, \quad b=-\dfrac{1}{5}-\dfrac{\sqrt{19}}{5} i\)
请记住,要使用二次公式,方程必须以标准形式书写\(a x^{2}+b x+c=0\)。 有时,我们需要先做一些代数才能使方程变为标准形式,然后才能使用二次公式。
使用二次公式求解:\(x(x+6)+4=0\).
解决方案:
我们的第一步是获得标准形式的方程式。
 |
|
| 分布以获得标准形式的方程。 |  |
| 这个方程现在是标准形式。 |  |
| 确定的值\(a,b,c\)。 |  |
| 写下二次方程式。 | 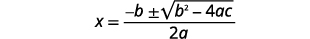 |
| 然后替换为的值\(a,b,c\)。 | 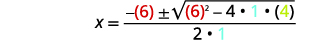 |
| 简化。 | 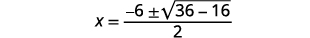 |
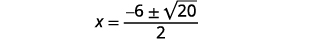 |
|
| 简化激进。 | 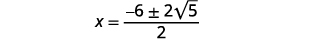 |
| 将分子中的公因子分解。 | 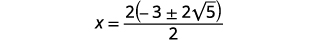 |
| 移除常见因素。 | 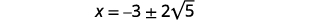 |
| 写成两个解决方案。 | 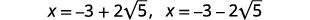 |
|
查看: 我们把支票留给你! |
使用二次公式求解:\(x(x+2)−5=0\).
- 回答
-
\(x=-1+\sqrt{6}, x=-1-\sqrt{6}\)
使用二次公式求解:\(3y(y−2)−3=0\).
- 回答
-
\(y=1+\sqrt{2}, y=1-\sqrt{2}\)
当我们求解线性方程时,如果一个方程有太多的分数,我们会通过将方程的两边乘以 LCD 来清除分数。 这给了我们一个等效方程——没有分数——需要求解。 我们可以对二次方程使用相同的策略。
使用二次公式求解:\(\dfrac{1}{2} u^{2}+\dfrac{2}{3} u=\dfrac{1}{3}\).
解决方案:
我们的第一步是清除分数。
 |
|
| 将两边乘以液晶屏\(6\),以清除分数。 | 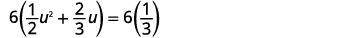 |
| 乘以。 |  |
| 减去\(2\)即可得到标准形式的方程式。 |  |
| 确定\(a, b\)、和的值\(c\)。 |  |
| 写下二次方程式。 | 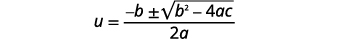 |
| 然后用\(a, b,\)和的值代替\(c\)。 | 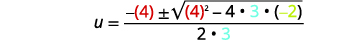 |
| 简化。 | 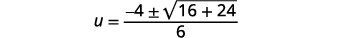 |
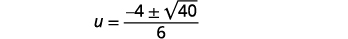 |
|
| 简化激进。 | 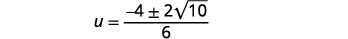 |
| 将分子中的公因子分解。 | 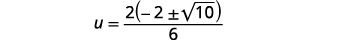 |
| 移除常见因素。 | 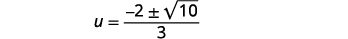 |
| 重写以显示两个解决方案。 | 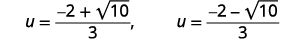 |
|
查看: 我们把支票留给你! |
使用二次公式求解:\(\dfrac{1}{4} c^{2}-\dfrac{1}{3} c=\dfrac{1}{12}\).
- 回答
-
\(c=\dfrac{2+\sqrt{7}}{3}, \quad c=\dfrac{2-\sqrt{7}}{3}\)
使用二次公式求解:\(\dfrac{1}{9} d^{2}-\dfrac{1}{2} d=-\dfrac{1}{3}\).
- 回答
-
\(d=\dfrac{9+\sqrt{33}}{4}, d=\dfrac{9-\sqrt{33}}{4}\)
想想这个方程式\((x-3)^{2}=0\)。 我们从零积属性中知道这个方程只有一个解,即\(x=3\)。
在下一个示例中,我们将看到如何使用二次公式求解标准形式为完美平方三项式等于的方程只能得\(0\)出一个解。 请注意,一旦简化了 radicand\(0\),它就会变成,这导致只有一个解。
使用二次公式求解:\(4 x^{2}-20 x=-25\).
解决方案:
 |
|
| 添加\(25\)即可获得标准形式的方程式。 |  |
| 确定\(a, b\)、和的值\(c\)。 |  |
| 写下二次方程式。 | 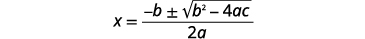 |
| 然后用\(a, b\)、和的值替换\(c\)。 |  |
| 简化。 | 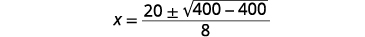 |
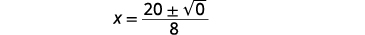 |
|
| 简化激进。 |  |
| 简化分数。 |  |
|
查看: 我们把支票留给你! |
你有没有意识到\(4 x^{2}-20 x+25\)这是一个完美的方形三项式。 它等同于\((2 x-5)^{2}\)? 如果你\(4 x^{2}-20 x+25=0\)通过分解然后使用平方根属性求解,你会得到相同的结果吗?
使用二次公式求解:\(r^{2}+10 r+25=0\).
- 回答
-
\(r=-5\)
使用二次公式求解:\(25 t^{2}-40 t=-16\).
- 回答
-
\(t=\dfrac{4}{5}\)
使用判别法预测二次方程解的数目和类型
当我们在前面的例子中求解二次方程时,有时会得到两个实解,一个实解,有时还有两个复杂解。 有没有办法在不实际求解方程的情况下预测二次方程解的数量和类型?
是的,二次方程式的基数下的表达式使我们很容易确定解的数量和类型。 这个表达式被称为判别词。
判别性

让我们来看看一些示例中方程的判别值以及这些二次方程解的数量和类型。
| 二次方程(标准形式) | 歧视\(b^{2}-4ac\) | 判别值的值 | 解决方案的数量和类型 |
|---|---|---|---|
| \(2 x^{2}+9 x-5=0\) | \ (b^ {2} -4ac\)” >\(\begin{aligned} 9^{2}-& 4 \cdot 2(-5) \\ & 121 \end{aligned}\) | \(+\) | \(2\)真实的 |
| \(4 x^{2}-20 x+25=0\) | \ (b^ {2} -4ac\)” >\((-20)^{2}-4 \cdot 4 \cdot 25\) \(0\) |
\(0\) | \(1\)真实的 |
| \(3 p^{2}+2 p+9=0\) | \ (b^ {2} -4ac\)” >\(2^{2}-4 \cdot 3 \cdot 9\) \(-104\) |
\(-\) | \(2\)复杂 |

使用判别\(b^{2}-4ac\)法确定二次方程解的数目和类型
对于形式的二次方程\(ax^{2}+bx+c=0\)\(a \neq 0\),
- 如果\(b^{2}-4 a c>0\),则方程具有\(2\)实解。
- if\(b^{2}-4 a c=0\),方程有\(1\)实解。
- if\(b^{2}-4 a c<0\),该方程具有\(2\)复数解。
确定每个二次方程的解数。
- \(3 x^{2}+7 x-9=0\)
- \(5 n^{2}+n+4=0\)
- \(9 y^{2}-6 y+1=0\)
解决方案:
为了确定每个二次方程的解数,我们将研究其判别值。
一个。
\(3 x^{2}+7 x-9=0\)
方程采用标准形式,请识别\(a, b\)和\(c\)。
\(a=3, \quad b=7, \quad c=-9\)
写下判别词。
\(b^{2}-4 a c\)
替换\(a, b\)、和的值\(c\)。
\((7)^{2}-4 \cdot 3 \cdot(-9)\)
简化。
\(49+108\)
\(157\)
由于判别值为正,因此该方程有\(2\)实际解。
b。
\(5 n^{2}+n+4=0\)
方程采用标准形式,请识别\(a, b\)和\(c\)。
\(a=5, \quad b=1, \quad c=4\)
写下判别词。
\(b^{2}-4 a c\)
替换\(a, b\)、和的值\(c\)。
\((1)^{2}-4 \cdot 5 \cdot 4\)
简化。
\(1-80\)
\(-79\)
由于判别值为负,因此该方程有\(2\)复杂的解。
c。
\(9 y^{2}-6 y+1=0\)
方程采用标准形式,请识别\(a, b\)和\(c\)。
\(a=9, \quad b=-6, \quad c=1\)
写下判别词。
\(b^{2}-4 a c\)
替换\(a, b\)、和的值\(c\)。
\((-6)^{2}-4 \cdot 9 \cdot 1\)
简化。
\(36-36\)
\(0\)
既然判别是\(0\),这个方程就有了\(1\)真正的解。
确定每个二次方程解的数量和类型。
- \(8 m^{2}-3 m+6=0\)
- \(5 z^{2}+6 z-2=0\)
- \(9 w^{2}+24 w+16=0\)
- 回答
-
- \(2\)复杂的解决方案
- \(2\)真正的解决方案
- \(1\)真正的解决方案
确定每个二次方程解的数量和类型。
- \(b^{2}+7 b-13=0\)
- \(5 a^{2}-6 a+10=0\)
- \(4 r^{2}-20 r+25=0\)
- 回答
-
- \(2\)真正的解决方案
- \(2\)复杂的解决方案
- \(1\)真正的解决方案
确定用于求解二次方程的最合适方法
我们在下面总结了用于求解二次方程的四种方法。
求解二次方程的方法
- 保理
- 平方根属性
- 完成正方形
- 二次方程式
鉴于我们有四种方法可以用来求解二次方程,那么你如何决定使用哪一种呢? 保理通常是最快的方法,所以我们先尝试一下。 如果方程为,\(ax^{2}=k\)或者\(a(x−h)^{2}=k\)我们使用平方根属性。 对于任何其他方程,最好使用二次公式。 请记住,你可以使用二次公式求解任何二次方程,但这并不总是最简单的方法。
那么完成方块的方法呢? 大多数人觉得这种方法很麻烦,宁愿不使用它。 我们需要将其包含在方法列表中,因为我们通常完成了方程式以得出二次公式。 你还将在其他代数区域使用完成正方形的过程。
确定求解二次方程的最合适方法
- 先试试保理。 如果二次因素很容易,则此方法非常快。
- 接下来试试平方根属性。 如果方程符合\(ax^{2}=k\)或的形式\(a(x−h)^{2}=k\),则可以使用平方根属性轻松求解。
- 使用二次方程式。 任何其他二次方程最好使用二次公式求解。
下一个示例使用此策略来决定如何求解每个二次方程。
确定用于求解每个二次方程的最合适方法。
- \(5 z^{2}=17\)
- \(4 x^{2}-12 x+9=0\)
- \(8 u^{2}+6 u=11\)
解决方案:
一个。
\(5z^{2}=17\)
由于方程在中\(ax^{2}=k\),因此最合适的方法是使用平方根属性。
b。
\(4 x^{2}-12 x+9=0\)
我们认识到,方程的左侧是一个完美的方形三项式,因此分解将是最合适的方法。
c。
\(8 u^{2}+6 u=11\)
将方程式以标准形式表示。
\(8 u^{2}+6 u-11=0\)
虽然我们首先想到的可能是尝试分解,但考虑反复试验法的所有可能性会导致我们选择二次方程式作为最合适的方法。
确定用于求解每个二次方程的最合适方法。
- \(x^{2}+6 x+8=0\)
- \((n-3)^{2}=16\)
- \(5 p^{2}-6 p=9\)
- 回答
-
- 保理
- 平方根属性
- 二次方程式
确定用于求解每个二次方程的最合适方法。
- \(8 a^{2}+3 a-9=0\)
- \(4 b^{2}+4 b+1=0\)
- \(5 c^{2}=125\)
- 回答
-
- 二次方程式
- 分解或平方根属性
- 平方根属性
访问这些在线资源以获取更多指导和使用二次公式进行练习。
关键概念
- 二次方程式
- 这种形式的\(a x^{2}+b x+c=0, a \neq 0\)二次方程的解由以下公式给出:
\(x=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\)
- 这种形式的\(a x^{2}+b x+c=0, a \neq 0\)二次方程的解由以下公式给出:
- 如何使用二次公式求解二次方程。
- 以标准形式写下二次方程\(a x^{2}+b x+c=0\)。 确定的值\(a, b, c\)。
- 写下二次方程式。 然后替换为的值\(a, b, c\)。
- 简化。
- 检查解决方案。
- 使用判别来确定二次方程解的数目和类型\(b^{2}-4 a c\)
- 对于这种形式的二次方程\(a x^{2}+b x+c=0, a \neq 0\),
- 如果\(b^{2}-4 a c>0\),则方程具有\(2\)实解。
- 如果\(b^{2}-4 a c=0\),则方程具有\(1\)实解。
- 如果\(b^{2}-4 a c<0\),则方程具有\(2\)复数解。
- 对于这种形式的二次方程\(a x^{2}+b x+c=0, a \neq 0\),
- 求解二次方程的方法:
- 保理
- 平方根属性
- 完成正方形
- 二次方程式
- 如何确定求解二次方程的最合适方法。
- 先试试保理。 如果二次因素很容易,则此方法非常快。
- 接下来试试平方根属性。 如果方程符合\(a x^{2}=k\)或的形式\(a(x-h)^{2}=k\),则可以使用平方根属性轻松求解。
- 使用二次方程式。 任何其他二次方程最好使用二次公式求解。
词汇表
- 判别的
- 在二次公式中\(x=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\),量\(b^{2}-4 a c\)称为判别值。