9.3:通过完成正方形求解二次方程
- Page ID
- 204135
在本节结束时,您将能够:
- 完成二项式表达式的平方
- \(x^{2}+bx+c=0\)通过完成正方形求解表格的二次方程
- \(ax^{2}+bx+c=0\)通过完成正方形求解表格的二次方程
在开始之前,请参加这个准备测验。
- 扩展:\((x+9)^{2}\)。
如果您错过了此问题,请查看示例 5.32。 - 因子\(y^{2}-14 y+49\)。
如果您错过了此问题,请查看示例 6.9。 - 因子\(5 n^{2}+40 n+80\)。
如果您错过了此问题,请查看示例 6.14。
到目前为止,我们已经通过分解和使用平方根属性求解了二次方程。 在本节中,我们将通过一个称为完成正方程的过程求解二次方程,这对于我们以后的圆锥研究很重要。
完成二项式表达式的平方
在最后一节中,我们能够使用平方根属性来求解方程,\((y-7)^{2}=12\)因为左边是一个完美的正方形。
\(\begin{aligned}(y-7)^{2} &=12 \\ y-7 &=\pm \sqrt{12} \\ y-7 &=\pm 2 \sqrt{3} \\ y &=7 \pm 2 \sqrt{3} \end{aligned}\)
我们还求解了一个方程,其中左侧是一个完美的三项方程,但是\((x−k)^{2}\)为了使用平方根属性,我们必须将其重写为形式。
\(\begin{aligned} x^{2}-10 x+25 &=18 \\(x-5)^{2} &=18 \end{aligned}\)
如果变量不是完美正方形的一部分会发生什么? 我们可以用代数来做一个完美的正方形吗?
让我们看两个例子来帮助我们识别模式。
\(\begin{array}{cc}{(x+9)^{2}} & {(y-7)^{2}} \\ {(x+9 )(x+9)} & {(y-7)(y-7)} \\ {x^{2}+9 x+9 x+81} & {y^{2}-7 y-7 y+49} \\ {x^{2}+18 x+81} & {y^{2}-14 y+49}\end{array}\)
我们在这里重述这些模式以供参考。
如果\(a\)和\(b\)是实数,
我们可以使用这种图案来 “制作” 一个完美的正方形。
我们将从表达式开始\(x^{2}+6 x\)。 由于两个术语之间有一个加号,我们将使用\((a+b)^{2}\)模式,\(a^{2}+2 a b+b^{2}=(a+b)^{2}\)。
我们最终需要找到这个三项式的最后一个项,使它成为一个完美的方形三项式。 要做到这一点,我们需要找到\(b\)。 但首先我们从确定开始\(a\)。 请注意,的第一个项\(x^{2}+6x\)是正方形\(x^{2}\)。 这告诉我们这一点\(a=x\)。
当与之相乘时\(b\),得\(2x\)出的是什么数字\(6x\)? 一定是这样\(3\),也就是说\(\frac{1}{2}(6)\)。 所以\(b=3\)。
现在要完成完美平方三项式,我们将通过平方来找到最后一个项\(b\),也就是说\(3^{2}=9\)。
我们现在可以考虑了。
所以我们发现添加\(9\)到\(x^{2}+6 x\) “完成正方形”,我们把它写成\((x+3)^{2}\)。
- 确定\(b\),系数\(x\)。
- 查找\(\left(\frac{1}{2} b\right)^{2}\),完成正方形的数字。
- 将添加\(\left(\frac{1}{2} b\right)^{2}\)到\(x^{2}+bx\)。
- 将完美的三项方分解出来,将其写成二项式的平方。
完成正方形以形成完美的三项式方形。 然后将结果写成二项式平方。
- \(x^{2}-26 x\)
- \(y^{2}-9 y\)
- \(n^{2}+\frac{1}{2} n\)
解决方案:
一个。
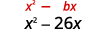 |
|
| 的系数\(x\)为 -26。 | |
|
查找\(\left(\frac{1}{2} b\right)^{2}\)。 \(\left(\frac{1}{2} \cdot(-26)\right)^{2}\) |
|
| \(169\)添加到二项式以完成正方形。 |
\(x^{2}-26 x+169\) |
| 将完美的三项方分解出来,将其写成二项式的平方。 |
\((x-13)^{2}\) |
b。
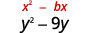 |
|
| 的系数\(y\)为\(-9\)。 | |
|
查找\(\left(\frac{1}{2} b\right)^{2}\)。 \(\left(\frac{1}{2} \cdot(-9)\right)^{2}\) |
|
| \(\frac{81}{4}\)添加到二项式以完成正方形。 |
\(y^{2}-9 y+\frac{81}{4}\) |
| 将完美的三项方分解出来,将其写成二项式的平方。 |
\(\left(y-\frac{9}{2}\right)^{2}\) |
c。
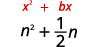 |
|
| 的系数\(n\)为\(\frac{1}{2}\)。 | |
|
查找\(\left(\frac{1}{2} b\right)^{2}\)。 \(\left(\frac{1}{2} \cdot \frac{1}{2}\right)^{2}\) |
|
| \(\frac{1}{16}\)添加到二项式以完成正方形。 | \(n^{2}+\frac{1}{2} n+\frac{1}{16}\) |
| 重写为二项式方块。 | \(\left(n+\frac{1}{4}\right)^{2}\) |
完成正方形以形成完美的三项式方形。 然后将结果写成二项式平方。
- \(a^{2}-20 a\)
- \(m^{2}-5 m\)
- \(p^{2}+\frac{1}{4} p\)
- 回答
-
- \((a-10)^{2}\)
- \(\left(b-\frac{5}{2}\right)^{2}\)
- \(\left(p+\frac{1}{8}\right)^{2}\)
完成正方形以形成完美的三项式方形。 然后将结果写成二项式平方。
- \(b^{2}-4 b\)
- \(n^{2}+13 n\)
- \(q^{2}-\frac{2}{3} q\)
- 回答
-
- \((b-2)^{2}\)
- \(\left(n+\frac{13}{2}\right)^{2}\)
- \(\left(q-\frac{1}{3}\right)^{2}\)
\(x^{2}+bx+c=0\)通过完成正方形求解表格的二次方程
在求解方程时,我们必须始终对方程的两边做同样的事情。 当然,当我们通过完成方程来求解二次方程时,情况也是如此。 当我们在方程的一侧添加一个项以形成完美的三项方形时,我们还必须将相同的项添加到方程的另一边。
例如,如果我们从方程开始\(x^{2}+6x=40\),想要完成左边的正方形,我们将在方程的两边加 9。
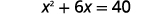 |
|
 |
|
 |
|
| \(9\)向两边添加即可完成正方形。 | 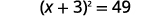 |
现在,方程的形式是使用平方根属性求解的! 完成正方形是将方程转换为我们能够使用平方根属性所需的形式的一种方法。
通过完成方块求解:\(x^{2}+8x=48\).
解决方案:
| 步骤 1:分离一侧的变量项和另一侧的常量项。 | 这个方程的所有变量都在左边。 | \(\begin{array}{l}{\color{red}{x^{2}+b x\quad\:\:\: c }} \\ {x^{2}+8 x=48}\end{array}\) |
| 步骤2:找到\(\left(\frac{1}{2} \cdot b\right)^{2}\),完成正方形的数字。 将其添加到方程的两边。 |
取一半\(8\)然后把它弄成平方。 \(4^{2}=16\) 加\(16\)到等式的两边。 |
\(x^{2}+8 x+\frac{}{\color{red}{\left(\frac{1}{2} \cdot 8\right)^{2}}}\color{black}{=}48 \) \(x^{2}+8 x\color{red}{+16}\color{black}{=}48\color{red}{+16}\) |
| 第 3 步:将完美的三项方形分解为二项式正方形。 |
\(x^{2}+8 x+16=(x+4)^{2}\) 在右侧添加条款。 |
\((x+4)^{2}=64\) |
| 步骤 4:使用平方根属性。 | \(x+4=\pm \sqrt{64}\) | |
| 步骤 5:简化基数,然后求解两个由此产生的方程。 |
\(x+4=\pm 8\) \(\begin{aligned} x+4 &=8 \quad x+4=-8 \\ x &=4 \quad\quad\:\:\: x=-12 \end{aligned}\) |
|
| 第 6 步:检查解决方案。 | 将每个答案放在原始方程式中进行检查。 替换\(x=4\)和\(x=-12\). |
\(\begin{array}{r}{x^{2}+8 x=48} \\ {(\color{red}{4}\color{black}{)}^{2}+8(\color{red}{4}\color{black}{)} \stackrel{?}{=} 48} \\ {16+32\stackrel{?}{=}48} \\ {48=48}\end{array}\) \(\begin{array}{r}{x^{2}+8 x=48} \\ {(\color{red}{-12}\color{black}{)}^{2}+8(\color{red}{-12}\color{black}{)}\stackrel{?}{=} 48} \\ {144-96 \stackrel{?}{=} 48} \\ {48=48}\end{array}\) |
通过完成方块求解:\(x^{2}+4 x=5\).
- 回答
-
\(x=-5, x=-1\)
通过完成方块求解:\(y^{2}−10y=−9\).
- 回答
-
\(y=1, y=9\)
此处列出了通过完成方程求解二次方程的步骤。
\(x^{2}+bx+c=0\)通过完成正方形求解形状的二次方程
- 分离一侧的变量项和另一侧的常量项。
- 查找\(\left(\frac{1}{2} \cdot b\right)^{2}\),完成正方形所需的数字。 将其添加到方程的两边。
- 将完美的正方形三项式分解,将其写成左边的二项式平方,然后通过在右边添加项来进行简化
- 使用平方根属性。
- 简化基数,然后求解两个由此产生的方程。
- 检查解决方案。
当我们通过完成正方形求解方程时,答案并不总是整数。
通过完成方块求解:\(x^{2}+4 x=-21\).
解决方案:
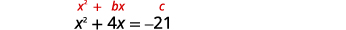 |
|
|
变量项在左边。 取一半\(4\)然后把它弄成平方。 |
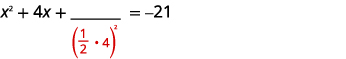 |
| \(\left(\frac{1}{2}(4)\right)^{2}=4\) | |
| 两\(4\)边都加上。 |  |
| 将完美的三项方分解出来,将其写成二项式的平方。 | 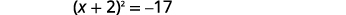 |
| 使用平方根属性。 | 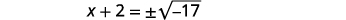 |
| 使用复数进行简化。 | 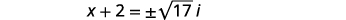 |
| \(2\)从两边减去。 | 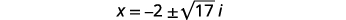 |
| 重写以显示两个解决方案。 | 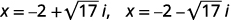 |
| 我们把支票留给你。 |
通过完成方块求解:\(y^{2}-10 y=-35\).
- 回答
-
\(y=5+\sqrt{15} i, y=5-\sqrt{15 i}\)
通过完成方块求解:\(z^{2}+8 z=-19\).
- 回答
-
\(z=-4+\sqrt{3} i, z=-4-\sqrt{3} i\)
在前面的示例中,我们的解是复数。 在下一个示例中,解将是非理性数。
通过完成方块求解:\(y^{2}-18 y=-6\).
解决方案:
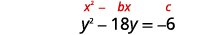 |
|
| 变量项在左边。 取一半\(-18\)然后把它弄成平方。 | |
| \(\left(\frac{1}{2}(-18)\right)^{2}=81\) | 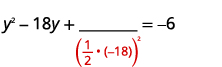 |
| 两\(81\)边都加上。 | 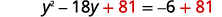 |
| 将完美的三项方分解出来,将其写成二项式的平方。 | 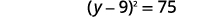 |
| 使用平方根属性。 | 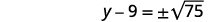 |
| 简化激进。 | 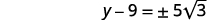 |
| 求解\(y\)。 |  |
|
查看。 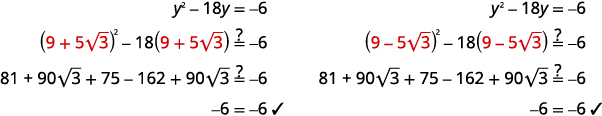
|
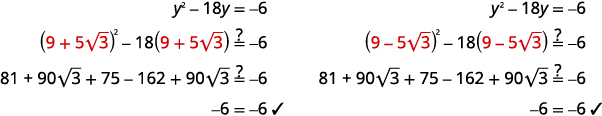 |
另一种检查方法是使用计算器。 \(y^{2}−18y\)评估这两种解决方案。 答案应该是\(−6\)。
通过完成方块求解:\(x^{2}-16 x=-16\).
- 回答
-
\(x=8+4 \sqrt{3}, x=8-4 \sqrt{3}\)
通过完成方块求解:\(y^{2}+8 y=11\).
- 回答
-
\(y=-4+3 \sqrt{3}, y=-4-3 \sqrt{3}\)
我们将从隔离方程左侧的变量项开始下一个示例。
通过完成方块求解:\(x^{2}+10 x+4=15\).
解决方案:
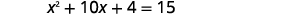 |
|
| 分离左侧的变量项。 减去\(4\)即可得到右侧的常量项。 | 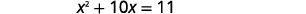 |
| 取一半\(10\)然后把它弄成平方。 | |
| \(\left(\frac{1}{2}(10)\right)^{2}=25\) | 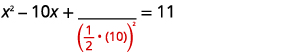 |
| 两\(25\)边都加上。 | 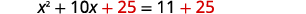 |
| 将完美的三项方分解出来,将其写成二项式的平方。 | 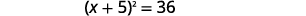 |
| 使用平方根属性。 | 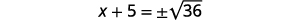 |
| 简化激进。 | 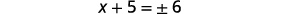 |
| 求解\(x\)。 | 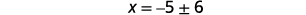 |
| 重写以显示两个解决方案。 | 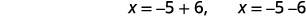 |
| 求解方程式。 | 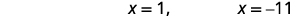 |
|
查看: 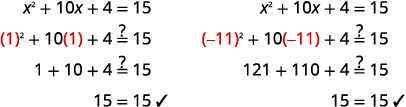
|
通过完成方块求解:\(a^{2}+4 a+9=30\).
- 回答
-
\(a=-7, a=3\)
通过完成方块求解:\(b^{2}+8 b-4=16\).
- 回答
-
\(b=-10, b=2\)
要求解下一个方程,我们必须首先收集方程左侧的所有变量项。 然后我们按照前面的示例继续操作。
通过完成方块求解:\(n^{2}=3 n+11\).
解决方案:
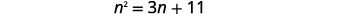 |
|
| 减\(3n\)去得到左侧的变量项。 |  |
| 取一半\(-3\)然后把它弄成平方。 | |
| \(\left(\frac{1}{2}(-3)\right)^{2}=\frac{9}{4}\) | 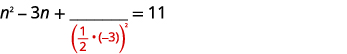 |
| 两\(\frac{9}{4}\)边都加上。 | 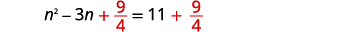 |
| 将完美的三项方分解出来,将其写成二项式的平方。 | 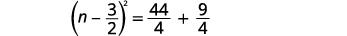 |
| 在右侧添加分数。 | 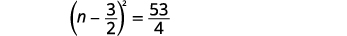 |
| 使用平方根属性。 | 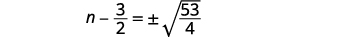 |
| 简化激进。 | 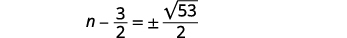 |
| 求解\(n\)。 | 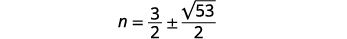 |
| 重写以显示两个解决方案。 | 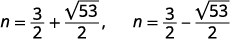 |
|
查看: 我们把支票留给你! |
通过完成方块求解:\(p^{2}=5 p+9\).
- 回答
-
\(p=\frac{5}{2}+\frac{\sqrt{61}}{2}, p=\frac{5}{2}-\frac{\sqrt{61}}{2}\)
通过完成方块求解:\(q^{2}=7 q-3\).
- 回答
-
\(q=\frac{7}{2}+\frac{\sqrt{37}}{2}, q=\frac{7}{2}-\frac{\sqrt{37}}{2}\)
请注意,下一个方程的左侧是因子形式。 但是右边不是零。 因此,我们不能使用零积属性,因为它显示 “如果\(a⋅b=0\),那么\(a=0\)或”\(b=0\)。 取而代之的是,我们将因子相乘,然后将方程转换为标准形式,通过完成方程来求解。
通过完成方块求解:\((x-3)(x+5)=9\).
解决方案:
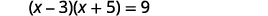 |
|
| 我们将左边的二项式相乘。 | 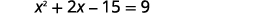 |
| 添加\(15\)以隔离右侧的常量项。 | 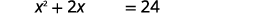 |
| 取一半\(2\)然后把它弄成平方。 | |
| \(\left(\frac{1}{2} \cdot(2)\right)^{2}=1\) | 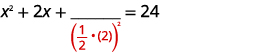 |
| 两\(1\)边都加上。 | 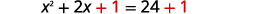 |
| 将完美的三项方分解出来,将其写成二项式的平方。 | 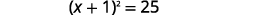 |
| 使用平方根属性。 | 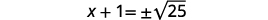 |
| 求解\(x\)。 | 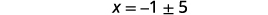 |
| 重写以显示两个解决方案。 | 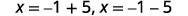 |
| 简化。 | 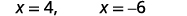 |
|
查看: 我们把支票留给你! |
通过完成方块求解:\((c-2)(c+8)=11\).
- 回答
-
\(c=-9, c=3\)
通过完成方块求解:\((d-7)(d+3)=56\).
- 回答
-
\(d=11, d=-7\)
\(ax^{2}+bx+c=0\)通过完成正方形求解表格的二次方程
当系数为时,完成正方形的\(x^{2}\)过程效果最好\(1\),因此方程左侧的形式为\(x^{2}+bx+c\)。 如果该\(x^{2}\)项的系数不是\(1\),则我们会采取一些初步步骤使系数等于\(1\)。
有时,系数可以从三项式的所有三个项中分解出来。 这将是我们在下一个例子中的策略。
通过完成方块求解:\(3 x^{2}-12 x-15=0\).
解决方案:
要完成平方,我们需要将的系数\(x^{2}\)设为一。 如果我们将的系数\(x^{2}\)作为公因子分解,我们可以通过完成方程来继续求解方程。
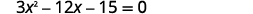 |
|
| 排除最大的共同因素。 | 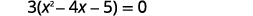 |
| 将两边除以\(3\)以分离带系数的三项式\(1\)。 | 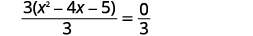 |
| 简化。 | 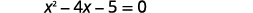 |
| \(5\)相加即可获得右侧的常量项。 | 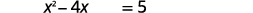 |
| 取一半\(4\)然后把它弄成平方。 | |
| \(\left(\frac{1}{2}(-4)\right)^{2}=4\) | 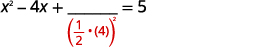 |
| 两\(4\)边都加上。 | 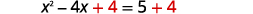 |
| 将完美的三项方分解出来,将其写成二项式的平方。 | 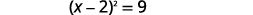 |
| 使用平方根属性。 | 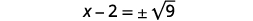 |
| 求解\(x\)。 | 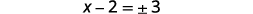 |
| 重写以显示两个解决方案。 | 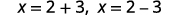 |
| 简化。 |  |
|
查看: 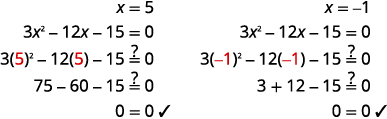
|
通过完成方块求解:\(2 m^{2}+16 m+14=0\).
- 回答
-
\(m=-7, m=-1\)
通过完成方块求解:\(4 n^{2}-24 n-56=8\).
- 回答
-
\(n=-2, n=8\)
要完成平方,的系数\(x^{2}\)必须为\(1\)。 当前导系数不是所有项的因子时,我们将把方程的两边除以前导系数! 这将为我们提供第二个系数的分数。 在本节中,我们已经看到了如何用分数完成正方形。
通过完成方块求解:\(2 x^{2}-3 x=20\).
解决方案:
要完成正方形,我们需要将的系数\(x^{2}\)设为一。 我们将方程的两边除以系数\(x^{2}\)。 然后我们可以通过完成方程来继续求解方程。
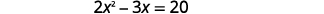 |
|
| 将两边除\(2\)以得出 to be\(x^{2}\) 的系数\(1\)。 | 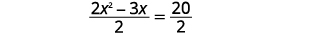 |
| 简化。 | 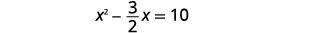 |
| 取一半\(-\frac{3}{2}\)然后把它弄成平方。 | |
| \(\left(\frac{1}{2}\left(-\frac{3}{2}\right)\right)^{2}=\frac{9}{16}\) | 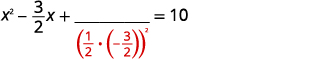 |
| 两\(\frac{9}{16}\)边都加上。 | 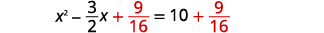 |
| 将完美的三项方分解出来,将其写成二项式的平方。 | 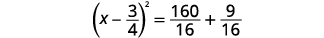 |
| 在右侧添加分数。 | 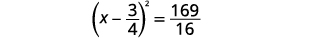 |
| 使用平方根属性。 | 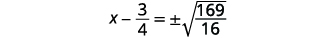 |
| 简化激进。 | 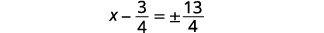 |
| 求解\(x\)。 | 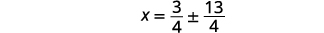 |
| 重写以显示两个解决方案。 | 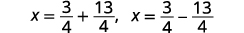 |
| 简化。 | 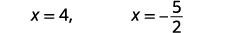 |
|
查看: 我们把支票留给你! |
通过完成方块求解:\(3 r^{2}-2 r=21\).
- 回答
-
\(r=-\frac{7}{3}, r=3\)
通过完成方块求解:\(4 t^{2}+2 t=20\).
- 回答
-
\(t=-\frac{5}{2}, t=2\)
既然我们已经看到,要完成正方形\(x^{2}\)必须\(1\)使用系数,我们更新了求解二次方程的程序,完成方程以包括形式的方程\(a x^{2}+b x+c=0\)。
- 除以 aa 得出\(x^{2}\)项系数\(1\)。
- 分离一侧的变量项和另一侧的常量项。
- 查找\(\left(\frac{1}{2} \cdot b\right)^{2}\),完成正方形所需的数字。 将其添加到方程的两边。
- 将完美的正方形三项式分解,将其写成左边的二项式平方,然后通过在右边添加项来进行简化
- 使用平方根属性。
- 简化基数,然后求解两个由此产生的方程。
- 检查解决方案。
通过完成方块求解:\(3 x^{2}+2 x=4\).
解决方案:
同样,我们的第一步将是将系数设\(x^{2}\)为 1。 通过将方程的两边除以系数\(x^{2}\),然后我们可以通过完成方程来继续求解方程。
 |
|
| 将两边除\(3\)以使系数\(x^{2}\)相等\(1\)。 | 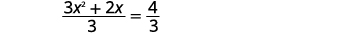 |
| 简化。 |  |
| 取一半\(\frac{2}{3}\)然后把它弄成平方。 | |
| \(\left(\frac{1}{2} \cdot \frac{2}{3}\right)^{2}=\frac{1}{9}\) | 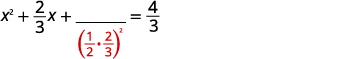 |
| 两\(\frac{1}{9}\)边都加上。 | 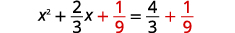 |
| 将完美的三项方分解出来,将其写成二项式的平方。 | 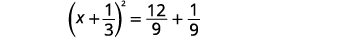 |
| 使用平方根属性。 | 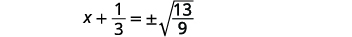 |
| 简化激进。 | 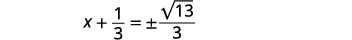 |
| 求解\(x\)。 | 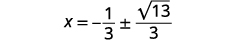 |
| 重写以显示两个解决方案。 | 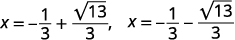 |
|
查看: 我们把支票留给你! |
通过完成方块求解:\(4 x^{2}+3 x=2\).
- 回答
-
\(x=-\frac{3}{8}+\frac{\sqrt{41}}{8}, x=-\frac{3}{8}-\frac{\sqrt{41}}{8}\)
通过完成方块求解:\(3 y^{2}-10 y=-5\).
- 回答
-
\(y=\frac{5}{3}+\frac{\sqrt{10}}{3}, y=\frac{5}{3}-\frac{\sqrt{10}}{3}\)
访问这些在线资源以获取更多指导和练习,完成方块即可。
关键概念
- 二项式方块模式
如果\(a\)和\(b\)是实数,
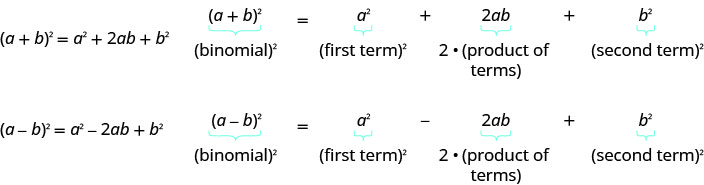
- 如何完成正方形
- 确定\(b\),系数\(x\)。
- 查找\(\left(\frac{1}{2} b\right)^{2}\),完成正方形的数字。
- 将添加\(\left(\frac{1}{2} b\right)^{2}\)到\(x^{2}+bx\)
- 将三项式重写为二项式正方形
- 如何\(a x^{2}+b x+c=0\)通过完成正方形来求解形状的二次方程。
- 除\(a\)以得出\(x^{2}\)项系数\(1\)。
- 分离一侧的变量项和另一侧的常量项。
- 查找\(\left(\frac{1}{2} \cdot b\right)^{2}\),完成正方形所需的数字。 将其添加到方程的两边。
- 将完美平方三项式分解出来,将其写成左边的二项式平方,然后通过在右边添加项来进行简化。
- 使用平方根属性。
- 简化基数,然后求解两个由此产生的方程。
- 检查解决方案。


