7.7: 解决理性不等式

Last updated
Save as PDF

Page ID: 204274

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

学习目标

解决理性不平等问题
用有理函数求解不等式

做好准备

在开始之前，请参加这个准备测验。

找出 when ⓐ$x=6$ ⓑ$x=-3$ ⓒ 的$x-5$值$x=5$
如果你错过了这个问题，请查看示例 1.2.16。
解决：$8-2 x<12$
如果您错过了此问题，请查看示例 2.6.13。
用间隔符号书写：$-3 \leq x<5 $
如果你错过了这个问题，请查看示例 2.6.4。

解决理性不等式

在学会求解线性方程之后，我们学会了求解线性不等式。除了一个主要的例外，这些技术大致相同。当我们乘以或除以负数时，不等式符号反转。

在学会了求解有理方程之后，我们现在已经准备好解决有理不等式了。理性不等式是包含理性表达的不等式。

理性不平等

理性不等式是包含理性表达的不等式。

$\quad \dfrac{3}{2 x}>1, \quad \dfrac{2 x}{x-3}<4, \quad \dfrac{2 x-3}{x-6} \geq x,\quad$和之类的不等式$\quad \dfrac{1}{4}-\dfrac{2}{x^{2}} \leq \dfrac{3}{x}\quad $是理性不等式，因为它们都包含理性表达。

当我们求解有理不等式时，我们将使用许多求解线性不等式的技术。我们尤其必须记住，当我们乘以或除以负数时，不等式符号必须反转。

另一个不同之处在于，我们必须仔细考虑什么价值可能使理性表达不明确，因此必须将其排除在外。

当我们求解一个方程并且结果是$x=3$，我们知道有一个解，那就是 3。

当我们解决不等式时$x>3$，结果是，我们知道有很多解决方案。我们绘制结果图以更好地帮助显示所有解决方案，我们从 3 开始。三个成为临界点，然后我们决定是向左还是向右遮挡。 3 右边的数字大于 3，所以我们向右加阴影。

$clipboard_e564fdf3437198939cd8bf44061cfa74e.png$

为了解决理性不等式，我们首先必须写出左边只有一个商而右边只有一个商的不等式。

接下来，我们确定用于将数字线划分为间隔的关键点。 临界点是使有理表达式为零或未定义的数字。

然后，我们将评估分子和分母的因子，并在每个区间中找到商。这将确定包含有理不等式所有解的区间或间隔。

我们用间隔表示法来写解，谨慎确定是否包含端点。

示例$\PageIndex{1}$

求解并用区间表示法写出解：$\dfrac{x-1}{x+3} \geq 0$

解决方案

第 1 步。将不等式写成左边的一商和右边的零。

我们的不平等就是这种形式。 \[\dfrac{x-1}{x+3} \geq 0 \nonumber \]

第 2 步。确定临界点，即有理表达式为零或未定义的点。

当分子为零时，有理表达式将为零。从那$x-1=0$时起$x=1$，1 就是临界点。

当分母为零时，有理表达式将未定义。从那$x+3=0$时起$x=-3$，-3就是临界点。

临界点为 1 和 -3。

第 3 步。使用临界点将数字线划分为间隔。

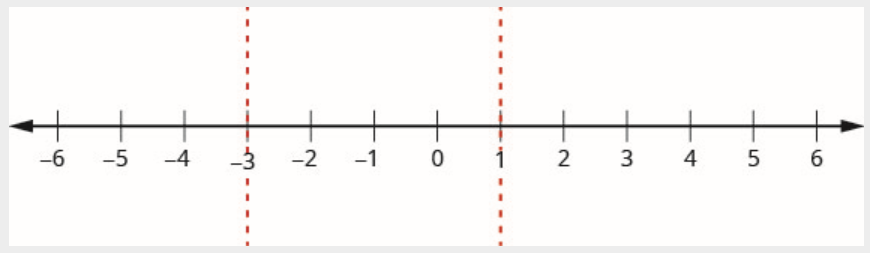
$clipboard_e431a0043d1c5bb7e4b4d0de15dc59cbc.png$

数字行分为三个间隔：

\[(-\infty,-3) \quad (-3,1) \quad (1,\infty) \nonumber \]

第 4 步。在每个间隔内测试一个值。数字线上方显示每个区间内有理表达式的每个因子的符号。数字线下方显示商的符号。

要找到区间中每个因子的符号，我们选择该区间中的任意点并将其用作测试点。区间中的任何点都将赋予表达式相同的符号，因此我们可以选择区间中的任何点。

\[\text { Interval }(-\infty,-3) \nonumber \]

数字 -4 在间隔内$(-\infty,-3)$。 $x=-4$在分子和分母中的表达式中进行测试。

分子：

\[\begin{array}{l} {x-1} \\ {-4-1} \\ {-5} \\ {\text {Negative}} \end{array} \nonumber \]

分母：

\[\begin{array}{l} {x+3} \\ {-4+3} \\ {-1} \\ {\text {Negative}} \end{array} \nonumber \]

在数字线上方，将系数标记为$x-1$负数，然后将系数标记为$x+3$负数。

由于负数除以负数为正数，因此在区间内将商标记为正数$(-\infty,-3)$

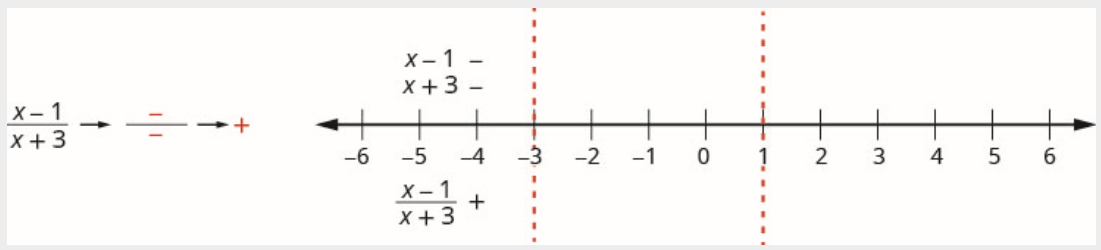
$clipboard_e4d5ff31fd44e4c2b9e0115f2b58099f8.png$

\[\text {Interval } (-3,1) \nonumber \]

数字 0 在间隔内$(-3,1)$。测试$x=0$。

分子：

\[\begin{array}{l} {x-1} \\ {0-1} \\ {-1} \\ {\text {Negative}} \end{array} \nonumber \]

分母：

\[\begin{array}{l} {x+3} \\ {0+3} \\ {3} \\ {\text {Positive}} \end{array} \nonumber \]

在数字线上方，将系数标记为$x-1$负数并标记为$x+3$正数。

由于负数除以正数为负数，因此在区间内商被标记为负数$(-3,1)$。

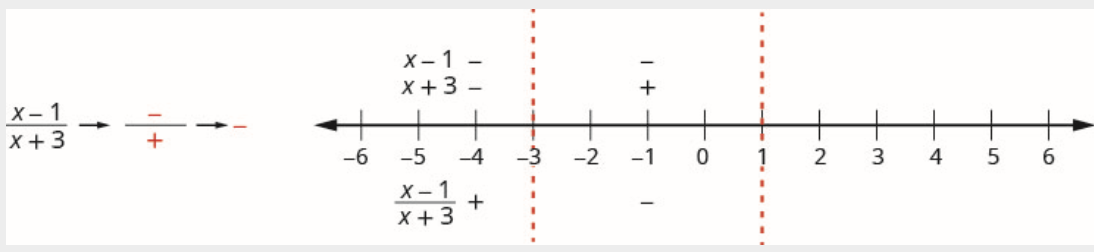
$clipboard_ee9a065f5ae1eb4312d2506f46f91b4f5.png$

\[\text {Interval }(1, \infty) \nonumber \]

数字 2 在间隔内$(1, \infty)$。测试$x=2$。

分子：

\[\begin{array}{l} {x-1} \\ {2-1} \\ {1} \\ {\text {Positive}} \end{array} \nonumber \]

分母：

\[\begin{array}{l} {x+3} \\ {2+3} \\ {5} \\ {\text {Positive}} \end{array} \nonumber \]

在数字线上方，将因子标记为$x-1$正数并标记为$x+3$正数。

由于正数除以正数为正数，因此在区间内将商标记为正数$(1, \infty)$。

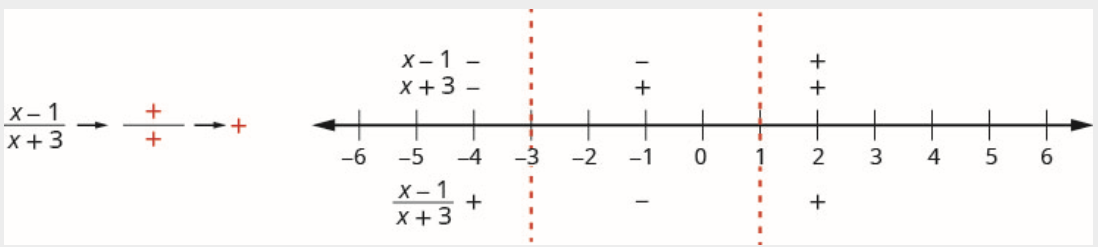
$clipboard_e9f05dbda07764ab489a7211f1b930f81.png$

第 5 步。确定不等式正确的间隔。用间隔表示法写出解。

我们希望商大于或等于零，因此区间$(-\infty,-3)$和中的数字$(1, \infty) $是解。

但是关键点呢？

临界点$x=-3$使分母为 0，因此必须将其排除在解之外，并用括号标记它。

临界点$x=1$使整个有理表达式为 0。不等式要求理性表达大于或等于。所以，1 是解决方案的一部分，我们将用方括号标记它。

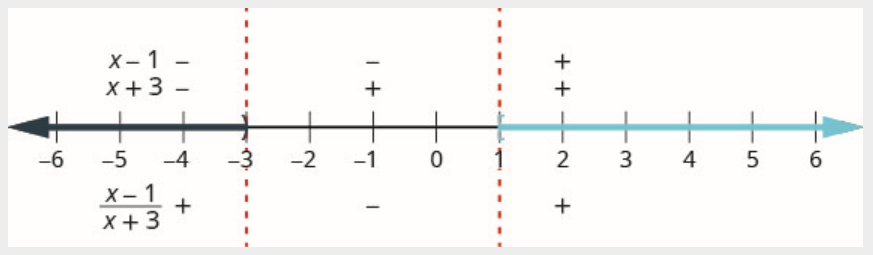
$clipboard_eff4e23ab54188da0d5229b26f9790bb8.png$

回想一下，当我们有一个由多个间隔组成的解时，我们使用并集符$\cup $号来连接两个间隔。区间表示法中的解是$(-\infty,-3) \cup[1, \infty)$。

练习$\PageIndex{1}$

求解并用区间表示法写出解：$\dfrac{x-2}{x+4} \geq 0$

回答: $(-\infty,-4) \cup[2, \infty)$

练习$\PageIndex{2}$

求解并用区间表示法写出解：$\dfrac{x+2}{x-4} \geq 0$

回答: $(-\infty,-2] \cup(4, \infty)$

我们总结了这些步骤以便于参考。

如何解决理性不平等

第 1 步。将不等式写成左边的一商和右边的零。

第 2 步。确定临界点，即有理表达式为零或未定义的点。

第 3 步。使用临界点将数字线划分为间隔。

第 4 步。在每个间隔内测试一个值。数字线上方显示每个间隔内分子和分母的每个因子的符号。数字线下方显示商的符号。

第 5 步。确定不等式正确的间隔。用间隔表示法写出解。

下一个例子要求我们首先将理性不等式转换为正确的形式。

示例$\PageIndex{2}$

求解并用区间表示法写出解：$\dfrac{4 x}{x-6}<1$

解决方案

\[\dfrac{4 x}{x-6}<1 \nonumber \]

减去 1 得到右边的零。

\[\dfrac{4 x}{x-6}-1<0 \nonumber \]

使用 LCD 将 1 重写为分数。

\[\dfrac{4 x}{x-6}-\frac{x-6}{x-6}<0 \nonumber \]

减去分子，然后将差值放在公分母上。

\[\dfrac{4 x-(x-6)}{x-6}<0 \nonumber \]

简化。

\[\dfrac{3 x+6}{x-6}<0 \nonumber \]

将分子分解以显示所有因子。

\[\dfrac{3(x+2)}{x-6}<0 \nonumber \]

找到关键点。

当分子为零时，商将为零。当分母为零时，商未定义。

\[\begin{array}{rlrl} {x+2} & {=0} & {x-6} & {=0} \\ {x} & {=-2} & {x} & {=6} \end{array} \nonumber \]

使用临界点将数字线划分为间隔。

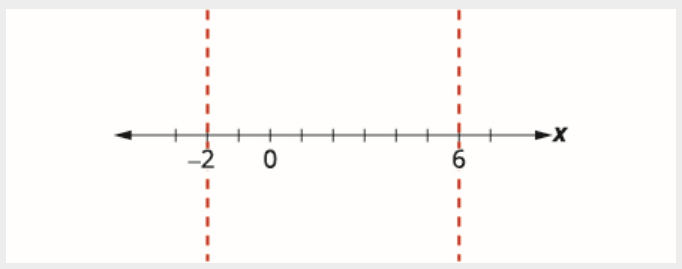
$clipboard_e21abd0b663d106757f6f6e723393df4e.png$

在每个间隔内测试一个值。

	\((-\infty,-2)\)	\((-2,6)\)	\((6, \infty)\)
\(x+2)\)	\ (-\ infty, -2)\)” style= “vertical-align: middle;” class= “lt-math-5164"> x+2 -3+2 -1 -	\ (-2,6)\)” style= “vertical-align: middle;” class= “lt-math-5164"> x+2 0+2 2 +	\ (6,\ infty)\)” style= “vertical-align: middle;” class= “lt-math-5164"> x+2 7+2 9 +
\(x-6\)	\ (-\ infty, -2)\)” style= “vertical-align: middle;” class= “lt-math-5164"> x-6 -3-6 -9 -	\ (-2,6)\)” style= “vertical-align: middle;” class= “lt-math-5164"> x-6 0-6 -6 -	\ (6,\ infty)\)” style= “vertical-align: middle;” class= “lt-math-5164"> x-6 7-6 1 +

$(-\infty,-2)$

$(-2,6)$

$(6, \infty)$

$x+2)$

\ (-\ infty, -2)\)” style= “vertical-align: middle;” class= “lt-math-5164">

x+2

-3+2

-1

\ (-2,6)\)” style= “vertical-align: middle;” class= “lt-math-5164">

x+2

0+2

\ (6,\ infty)\)” style= “vertical-align: middle;” class= “lt-math-5164">

x+2

7+2

$x-6$

\ (-\ infty, -2)\)” style= “vertical-align: middle;” class= “lt-math-5164">

x-6

-3-6

-9

\ (-2,6)\)” style= “vertical-align: middle;” class= “lt-math-5164">

x-6

0-6

-6

\ (6,\ infty)\)” style= “vertical-align: middle;” class= “lt-math-5164">

x-6

7-6

数字线上方显示每个区间内有理表达式的每个因子的符号。数字线下方显示商的符号。

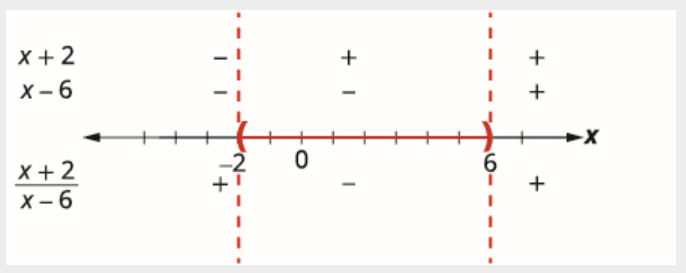
$clipboard_e667e7f41140a947d1fadb213a3b6434f.png$

确定不等式正确的间隔。我们希望商为负数，因此解包括介于 −2 和 6 之间的点。由于不等式严格小于，因此不包括端点。

我们将解用区间表示法写成 (−2, 6)。

练习$\PageIndex{3}$

求解并用区间表示法写出解:$\dfrac{3 x}{x-3}<1$.

回答: $\left(-\dfrac{3}{2}, 3\right)$

练习$\PageIndex{4}$

求解并用区间表示法写出解:$\dfrac{3 x}{x-4}<2$.

回答: $(-8,4)$

在下一个示例中，分子总是正数，因此有理表达式的符号取决于分母的符号。

示例$\PageIndex{3}$

求解并用区间表示法写出解:$\dfrac{5}{x^{2}-2 x-15}>0$.

解决方案

不等式的形式是正确的。

\[\dfrac{5}{x^{2}-2 x-15}>0 \nonumber \]

将分母系数考虑在内。

\[\dfrac{5}{(x+3)(x-5)}>0 \nonumber \]

找到关键点。当分子为 0 时，商为 0。由于分子始终为 5，因此商不能为 0。

当分母为零时，商将未定义。

\[\begin{aligned} &(x+3)(x-5)=0\\ &x=-3, x=5 \end{aligned} \nonumber \]

使用临界点将数字线划分为间隔。

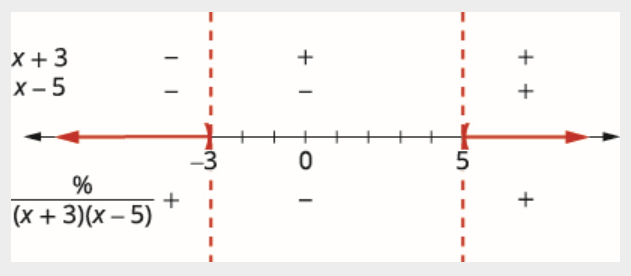
$clipboard_e021f22ee9a3dcabc95f9915aaa56196b.png$

每个间隔中的测试值。数字线上方显示每个间隔内分母的每个因子的符号。在数字线下方，显示商的符号。

用间隔表示法写出解。

\[(-\infty,-3) \cup(5, \infty) \nonumber \]

Exercise $\PageIndex{5}$

Solve and write the solution in interval notation: $\dfrac{1}{x^{2}+2 x-8}>0$.

Answer: $(-\infty,-4) \cup(2, \infty)$

Exercise $\PageIndex{6}$

Solve and write the solution in interval notation: $\dfrac{3}{x^{2}+x-12}>0 $.

Answer: $(-\infty,-4) \cup(3, \infty)$

The next example requires some work to get it into the needed form.

Example $\PageIndex{4}$

Solve and write the solution in interval notation: $\dfrac{1}{3}-\dfrac{2}{x^{2}}<\dfrac{5}{3 x}$.

Solution

\[\dfrac{1}{3}-\dfrac{2}{x^{2}}<\dfrac{5}{3 x} \nonumber \]

Subtract $\dfrac{5}{3 x}$ to get zero on the right.

\[\dfrac{1}{3}-\dfrac{2}{x^{2}}-\dfrac{5}{3 x}<0 \nonumber \]

Rewrite to get each fraction with the LCD

\[\dfrac{1 \cdot x^{2}}{3 \cdot x^{2}}-\dfrac{2 \cdot 3}{x^{2} \cdot 3}-\dfrac{5 \cdot x}{3 x-x}<0 \nonumber \]

Simplify.

\[\dfrac{x^{2}}{3 x^{2}}-\dfrac{6}{3 x^{2}}-\dfrac{5 x}{3 x^{2}}<0 \nonumber \]

Subtract the numerators and place the difference over the common denominator.

\[\dfrac{x^{2}-5 x-6}{3 x^{2}}<0 \nonumber \]

Factor the numerator.

\[\dfrac{(x-6)(x+1)}{3 x^{2}}<0 \nonumber \]

Find the critical points.

\[\begin{array}{rlrl} {3 x^{2}=0} && {x-6=0} && {x+1=0} \\ {x=0} && {x=6} && {x=-1} \end{array} \nonumber \]

Use the critical points to divide the number line into intervals.

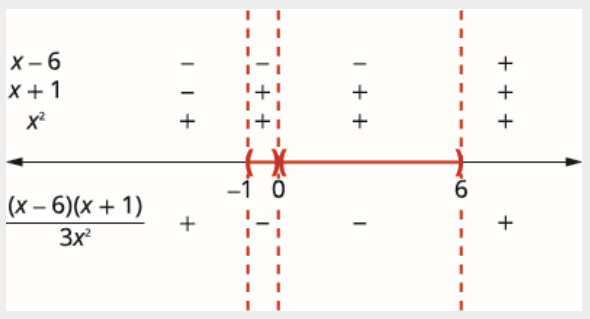
$clipboard_e782e665edacc8e08d9dc6bd0db2081e9.png$

数字线上方显示每个间隔中每个因子的符号。在数字线下方，显示商的符号。

由于排除 0，因此解是两个$(-1,0) \cup(0,6)$间隔，$(-1,0)$和$(0,6)$。

练习$\PageIndex{7}$

求解并用区间表示法写出解:$\dfrac{1}{2}+\dfrac{4}{x^{2}}<\dfrac{3}{x}$.

回答: $(2,4)$

练习$\PageIndex{8}$

求解并用区间表示法写出解:$\dfrac{1}{3}+\dfrac{6}{x^{2}}<\dfrac{3}{x}$.

回答: $(3,6)$

用有理函数求解不等式

在使用有理函数时，知道该函数何时大于或小于特定值有时很有用。这导致了理性的不平等。

示例$\PageIndex{5}$

给定函数$R(x)=\dfrac{x+3}{x-5}$，求出使函数小于或等于 0 的 x 值。

解决方案

我们希望该函数小于或等于 0。

\[R(x) \leq 0 \nonumber \]

用有理表达式代替$R(x)$。

\[\dfrac{x+3}{x-5} \leq 0 \quad x \neq 5 \nonumber \]

找到关键点。

\[\begin{array}{rlrl} {x+3=0} && {x-5=0} \\ {x=-3} && {x=5} \end{array} \nonumber \]

使用临界点将数字线划分为间隔。

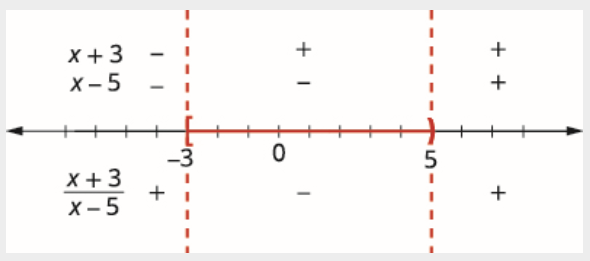
$clipboard_e76bb40ea8906c703f6c28ecf1b509d58.png$

每个间隔中的测试值。在数字线上方，显示每个间隔中每个因子的符号。在数字线下方，显示商的符号。用间隔表示法写出解。由于 5 被排除在外，因此请勿将其包含在间隔中。

\[[-3,5) \nonumber \]

Exercise $\PageIndex{9}$

Given the function $R(x)=\dfrac{x-2}{x+4}$, find the values of $x$ that make the function less than or equal to 0.

Answer: $(-4,2]$

Exercise $\PageIndex{10}$

Given the function $R(x)=\dfrac{x+1}{x-4}$, find the values of $x$ that make the function less than or equal to 0.

Answer: $[-1,4)$

In economics, the function $C(x)$ is used to represent the cost of producing $x$ units of a commodity. The average cost per unit can be found by dividing $C(x)$ by the number of items $x$. Then, the average cost per unit is \(c(x)=\dfrac{C(x)}{x}).

Example $\PageIndex{6}$

The function$C(x)=10 x+3000$ represents the cost to produce $x$, number of items. Find:

The average cost function, $c(x)$
How many items should be produced so that the average cost is less than $40.

Solution

\[C(x)=10 x+3000 \nonumber \]

The average cost function is $c(x)=\dfrac{C(x)}{x})$. To find the average cost function, divide the cost function by $x$.

\[\begin{aligned} &c(x)=\dfrac{C(x)}{x}\\ &c(x)=\dfrac{10 x+3000}{x} \end{aligned} \nonumber \]

The average cost function is $c(x)=\dfrac{10 x+3000}{x} $

We want the function $c(x)$ to be less than 40.

\[c(x)<40 \nonumber \]

Substitute the rational expression forc(x).

\[\dfrac{10 x+3000}{x}<40, \quad x \neq 0 \nonumber \]

Subtract 40 to get 0 on the right.

\[\dfrac{10 x+3000}{x}-40<0 \nonumber \]

Rewrite the left side as one quotient by finding the LCD and performing the subtraction.

\[\begin{aligned} \dfrac{10 x+3000}{x}-40\left(\dfrac{x}{x}\right) &<0\\ \dfrac{10 x+3000}{x}-\dfrac{40 x}{x} &<0\\ \dfrac{10 x+3000-40 x}{x} &<0 \\ \dfrac{-30 x+3000}{x} &<0 \end{aligned} \nonumber \]

Factor the numerator to show all factors.

\[\begin{array}{ll} {\dfrac{-30(x-100)}{x}<0} \\ {-30(x-100)=0} && {x=0} \end{array} \nonumber \]

Find the critical points.

\[\begin{array}{rl} {-30 \neq 0} & {x-100=0} \\ &{x=100} \end{array} \nonumber \]

More than 100 items must be produced to keep the average cost below $40 per item.

Exercise $\PageIndex{11}$

The function$C(x)=20 x+6000$ represents the cost to produce $x$, number of items. Find:

How many items should be produced so that the average cost is less than $60.

Answer

$c(x)=\dfrac{20 x+6000}{x}$
More than 150 items must be produced to keep the average cost below $60 per item.

Exercise $\PageIndex{12}$

The function$C(x)=5 x+900$ represents the cost to produce $x$, number of items. Find:

How many items should be produced so that the average cost is less than $20.

Answer

$c(x)=\dfrac{5 x+900}{x}$
More than 60 items must be produced to keep the average cost below $20 per item.

理性不平等

示例\(\PageIndex{1}\)

练习\(\PageIndex{1}\)

练习\(\PageIndex{2}\)

如何解决理性不平等

示例\(\PageIndex{2}\)

练习\(\PageIndex{3}\)

练习\(\PageIndex{4}\)

示例\(\PageIndex{3}\)

Exercise \(\PageIndex{5}\)

Exercise \(\PageIndex{6}\)

Example \(\PageIndex{4}\)

练习\(\PageIndex{7}\)

练习\(\PageIndex{8}\)

示例\(\PageIndex{5}\)

Exercise \(\PageIndex{9}\)

Exercise \(\PageIndex{10}\)

Example \(\PageIndex{6}\)

Exercise \(\PageIndex{11}\)

Exercise \(\PageIndex{12}\)