7.6：使用有理方程求解应用程序

学习目标

• 求解比例
• 求解相似图形的应用程序
• 解决均匀运动应用程序
• 解决工作申请
• 解决直接变异问题
• 解决逆变问题

注意

在开始之前，请参加这个准备测验。

1. 示例 2.2.13。 示例 2.5.13。 示例 2.2.9。

求解比例

当两个有理表达式相等时，将它们关联的方程称为比例。

比例

比例是形式的方程式$\dfrac{a}{b}=\dfrac{c}{d}$，其中$b \neq 0, d \neq 0$。

该比例被读$a$$b$$c$为 “原样”$d$。

该方程$\dfrac{1}{2}=\dfrac{4}{8}$是一个比例，因为两个分数是相等的。 比例读$\dfrac{1}{2}=\dfrac{4}{8}$作 “1 等于 2 就像 4 等于 8”。

由于比例是带有有理表达式的方程，因此我们将以与求解有理方程相同的方式求解比例。 我们将方程的两边乘以 LCD 以清除分数，然后求解由此产生的方程。

示例$\PageIndex{1}$

解决：$\dfrac{n}{n+14}=\dfrac{5}{7}$。

解决方案

$$\dfrac{n}{n+14}=\dfrac{5}{7}, \quad n \neq-14 \nonumber$$

将两边乘以 LCD。

$$7(n+14)\left(\dfrac{n}{n+14}\right)=7(n+14)\left(\dfrac{5}{7}\right) \nonumber$$

删除双方的共同因素。

$$7 n=5(n+14) \nonumber$$

简化。

$$7 n=5 n+70 \nonumber$$

求解$n$。

$$\begin{aligned} 2n&=70\\ n&=35 \end{aligned} \nonumber$$

查看。

$$\dfrac{n}{n+14}=\dfrac{5}{7} \nonumber$$

替代$n=35$

$$\dfrac{35}{35+14} \overset{?}{=} \dfrac{5}{7} \nonumber$$

简化。

$$\dfrac{35}{49} \overset{?}{=} \dfrac{5}{7} \nonumber$$

显示常见因素。

$$\dfrac{5 \cdot 7}{7 \cdot 7} \overset{?}{=} \dfrac{5}{7} \nonumber$$

简化。

$$\dfrac{5}{7}=\dfrac{5}{7}\; \surd \nonumber$$

练习$\PageIndex{1}$

求解比例:$\dfrac{y}{y+55}=\dfrac{3}{8}$.

回答

$y=33$

练习$\PageIndex{2}$

求解比例:$\dfrac{z}{z-84}=-\dfrac{1}{5}$.

回答

$z=14$

请注意，在最后一个示例中，当我们通过乘以 LCD 来清除分数时，结果与交叉乘法相同。

$$\begin{aligned} \dfrac{n}{n+14}=\dfrac{5}{7} \quad \quad \quad \dfrac{n}{n+14}=\dfrac{5}{7} \\ 7(n+14)\left(\dfrac{n}{n+14}\right)=7(n+14)\left(\dfrac{5}{7}\right) \quad \quad \quad \dfrac{n}{n+14}=\dfrac{5}{7} \\ 7n=5(n+14) \quad \quad \quad 7n=5(n+14) \end{aligned} \nonumber$$

对于任何比例$\dfrac{a}{b}=\dfrac{c}{d}$，当我们通过乘以液晶屏清除分数时，我们得到的结果与交叉乘法时得到的结果相同。

$$\begin{aligned} \dfrac{a}{b} =\dfrac{c}{d} \quad \quad \quad \dfrac{a}{b}=\dfrac{c}{d} \\ bd\left(\dfrac{a}{b}=\frac{c}{d}\right) bd \quad \quad \quad \frac{a}{b} = \frac{c}{d} \\ ad =bc \quad \quad \quad ad=bc \end{aligned} \nonumber$$

要使用比例求解应用程序，我们将遵循通常的策略来求解应用程序。但是当我们设置比率时，我们必须确保单位正确——分子中的单位必须相互匹配，分母中的单位也必须相互匹配。

当儿科医生给孩子开对乙酰氨基酚处方时，他们会为孩子每体重25磅开5毫升（ml）的对乙酰氨基酚处方。 如果佐伊体重 80 磅，她的医生会开多少毫升的对乙酰氨基酚处方？

解决方案

确定我们要查找的内容，然后选择一个变量来表示它。

医生会开多少毫升的对乙酰氨基酚？

放开$a=ml$对乙酰氨基酚。

写一句话，给出找到它的信息。

如果每 25 磅开出 5 毫升处方，那么 80 磅的处方是多少？

换算成比例——小心单位。

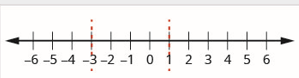
第 1 步。 将不等式写成左边的一商和右边的零。 我们的不平等就是这种形式。

$$\dfrac{x-1}{x+3} \geq 0 \nonumber$$

第 2 步。 确定临界点——有理表达式为零或未定义的点。

当分子为零时，有理表达式将为零。 从那$x-1=0$时起$x=1$，1 就是临界点。 当分母为零时，有理表达式将未定义。 从那$x+3=0$时起$x=-3$，-3就是临界点。

第 3 步。 使用临界点将数字线划分为间隔。

第 4 步。 数字线上方显示每个区间内有理表达式的每个因子的符号。 数字线下方显示商的符号。

使用每个区间中的值来确定区间中每个因子的值。 在间隔 (-3,1) 中，零是一个很好的检验值。 例如，wh$x=0$ en$x-1=-1$ 和 The 因$x+3=3$子标记$x-1$为负值并$x+3$标记为正数。 由于负数除以正数为负数，因此在该区间内，商被标记为负数。

第 5 步。 确定不等式正确的时间间隔。 用间隔表示法写出解。

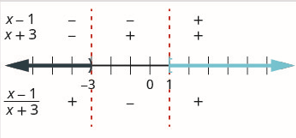
我们希望商大于或等于零，因此区间$(-\infty,-3)$和中的数字$(1, \infty)$是解。 由于必须排除 3，因为它使有理表达式为 0，因此我们不能将其包含在解中。 我们可以在解决方案中包含 1。

$$(-\infty,-3) \cup[1, \infty) \nonumber$$

将两边乘以液晶屏 400。 删除双方的共同因素。 简化，但不要在左边乘以。 注意下一步将是什么。

$$16 \cdot 5=5 a \nonumber$$

求解$a$。

$$\begin{aligned} \dfrac{16 \cdot 5}{5}&=\dfrac{5 a}{5}\\ 16&=a \end{aligned} \nonumber$$

查看。 答案合理吗？ 写一个完整的句子。

儿科医生会给佐伊开16毫升的对乙酰氨基酚处方。

练习$\PageIndex{3}$

儿科医生为孩子每体重 25 磅开出 5 毫升（ml）的对乙酰氨基酚处方。 医生会为体重60磅的艾米莉亚开多少毫升的对乙酰氨基酚处方？

回答

儿科医生会给艾米莉亚开12毫升对乙酰氨基酚的处方。

练习$\PageIndex{4}$

每增加一个孩子的体重 1 千克（kg），儿科医生就会开出 15 毫克（mg）的减烧剂。 如果伊莎贝拉体重12千克，儿科医生会开多少毫克的减烧药？

回答

儿科医生会给伊莎贝拉开180毫克的减烧药。

求解相似图形的应用程序

当你在手机或平板电脑上缩小或放大照片，在地图上计算出一段距离，或者使用图案制作书柜或缝制衣服时，你正在处理相似的人物。 如果两个数字的形状完全相同，但大小不同，则说它们是相似的。 一个是另一个的比例模型。 它们的所有对应角度都具有相同的测量值，并且它们对应的边具有相同的比例。

相似数字

如果两个图对应角度的测量值相等，并且它们对应的边的比率相同，则这两个数字是相似的。

例如，下图中的两个三角形是相似的。 的每一边$\Delta ABC$是相应边长度的四倍$\Delta XYZ$。

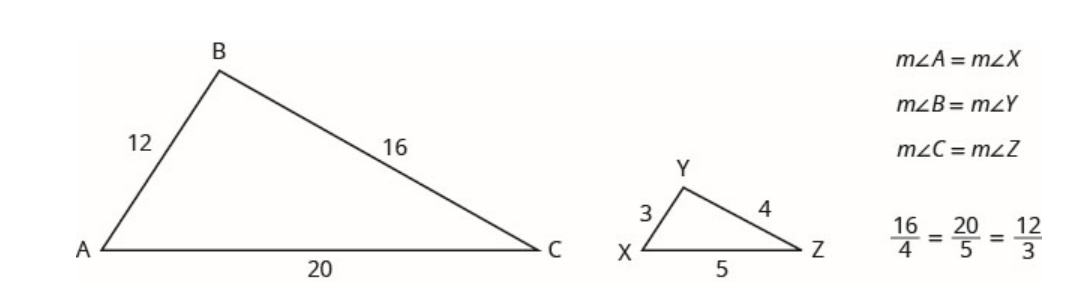
相似三角形的属性对此进行了总结。

相似三角形的属性

如果$\Delta ABC$与相似$\Delta XYZ$，则它们对应的角度测量值相等，并且它们对应的边具有相同的比率。

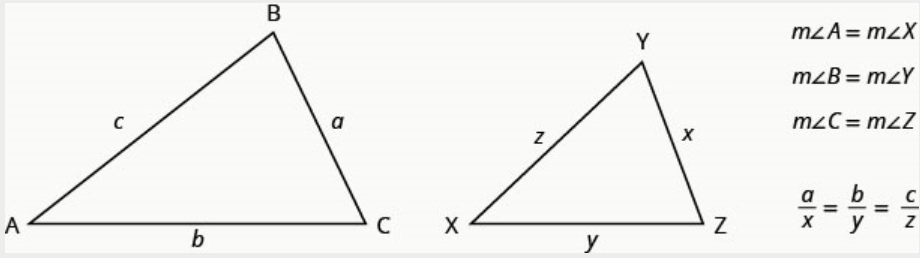
为了解决具有相似数字的应用程序，我们将遵循我们之前使用的几何应用程序问题解决策略。

示例$\PageIndex{3}$

在地图上，旧金山、拉斯维加斯和洛杉矶形成一个三角形。 城市之间的距离以英寸为单位测量。 下方左边的图表示地图上城市形成的三角形。 如果洛杉矶到拉斯维加斯的实际距离为 270 英里，请计算从洛杉矶到旧金山的距离。

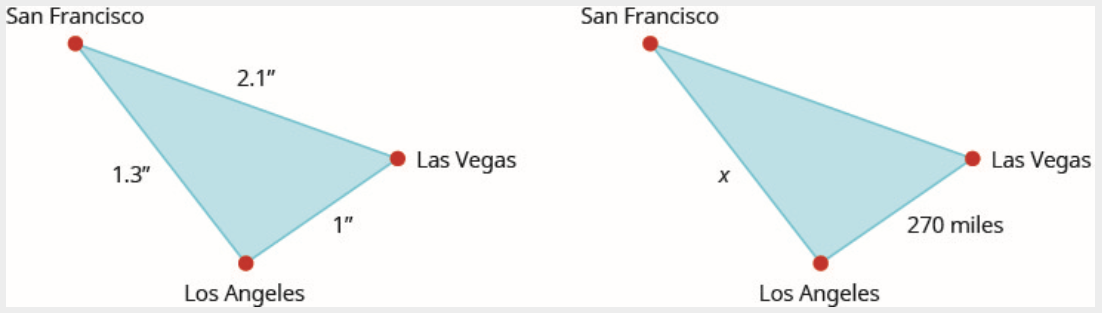
解决方案

由于三角形相似，因此相应的边是成比例的。

阅读问题。 绘制图形并用给定的信息对其进行标记。 数字如上所示。

确定我们在寻找什么：从洛杉矶到旧金山的实际距离

命名变量：让$x$ = 从洛杉矶到旧金山的距离。

翻译成方程式。 由于三角形相似，因此相应的边是成比例的。 我们将分子设为 “英里”，将分母设为 “英寸”。

$$$\dfrac{x \text { miles }}{1.3 \text { inches }}=\dfrac{270 \text { miles }}{1 \text { inch }}$ \nonumber$$

求解方程。

$$\begin{aligned} 1.3\left(\dfrac{x}{1.3}\right)&=1.3\left(\dfrac{270}{1}\right) \\ x&=351 \end{aligned} \nonumber$$

查看。 在地图上，从洛杉矶到旧金山的距离大于洛杉矶到拉斯维加斯的距离。 由于 351 大于 270，所以答案是有道理的。

检查$x=351$原始比例。 使用计算器。

$$\begin {aligned} \dfrac{x \text { miles }}{1.3 \text { inches }}&=\dfrac{270 \text { miles }}{1 \text { inch }}\\ \dfrac{351 \text { miles }}{1.3 \text { inches }} &\overset{?}{=} \dfrac{270 \text { miles }}{1 \text { inch }}\\ \dfrac{270 \text { miles }}{1 \text { inch }}&=\dfrac{270 \text { miles }}{1 \text { inch }} \surd \end{aligned} \nonumber$$

回答问题：从洛杉矶到旧金山的距离是351英里。

在地图上，西雅图、波特兰和博伊西形成一个三角形。 城市之间的距离以英寸为单位测量。 下方左边的图表示地图上城市形成的三角形。 从西雅图到博伊西的实际距离为 400 英里。

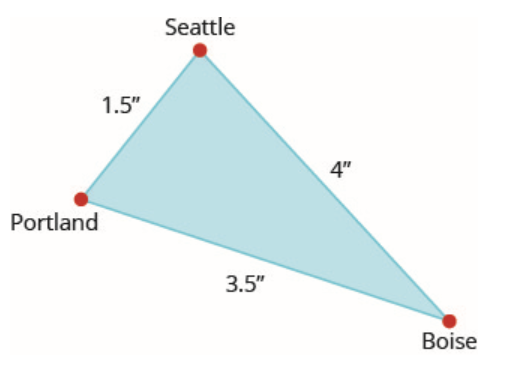
练习$\PageIndex{5}$

找出从西雅图到波特兰的实际距离。

回答

距离为 150 英里。

练习$\PageIndex{6}$

找出从波特兰到博伊西的实际距离。

回答

距离为 350 英里。

我们可以使用相似的数字来找到我们无法直接测量的高度。

示例$\PageIndex{4}$

泰勒身高 6 英尺。 一天下午晚些时候，他的影子长达 8 英尺。 同时，一棵树的阴影长达 24 英尺。 找出树的高度。

解决方案

阅读问题并画一个数字。 我们正在寻找$h$，树的高度。

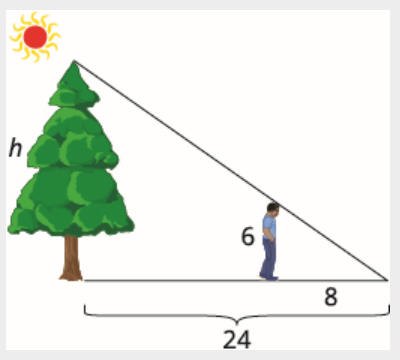
我们将使用相似的三角形来编写方程。 小三角形类似于大三角形。

$$\dfrac{h}{24}=\dfrac{6}{8} \nonumber$$

求解比例。

$$\begin {aligned} 24\left(\dfrac{6}{8}\right)&=24\left(\dfrac{h}{24}\right)\\ 18&=h \end{aligned} \nonumber$$

简化。 查看。

泰勒的高度小于他阴影的长度，所以树的高度小于其阴影的长度是有道理的。 检查$h=18$原始比例。

$$\begin{aligned} &\dfrac{6}{8}=\dfrac{h}{24}\\ &\dfrac{6}{8} \overset{?}{=} \dfrac{18}{24}\\ &\dfrac{3}{4}=\dfrac{3}{4} \surd \end{aligned} \nonumber$$

练习$\PageIndex{7}$

电线杆投射出 50 英尺长的阴影。 在附近，一个 8 英尺高的交通标志投射出 10 英尺长的阴影。 电线杆有多高？

回答

电线杆高 40 英尺。

练习$\PageIndex{8}$

一棵松树在一座30英尺高的建筑物旁边投射出80英尺的阴影，该建筑投射了40英尺的阴影。 那棵松树有多高？

回答

这棵松树高 60 英尺。

求解均匀运动应用程序

我们已经使用前面章节$D=r t$中的公式解决了均匀运动问题。 我们使用了如下所示的表格来整理信息并引导我们得出方程式。

	速率$\cdot$时间 = 距离
	\ (\ cdot\) 时间 = 距离” class= “lt-math-14671” >
	\ (\ cdot\) 时间 = 距离” class= “lt-math-14671” >

该公式$D=r t$假设我们知道$r$$t$并使用它们来查找$D$。 如果我们知道$D$$r$并且需要找到$t$，我们将求解方程$t$并得到公式$t=\dfrac{D}{r}$。

我们还解释了随风或逆风飞行如何影响飞机的速度。 我们将在下一个示例中重新审视这个想法。

示例$\PageIndex{5}$

一架飞机可以在 30 英里/小时的逆风中飞行 200 英里，其时间与在 30 英里/小时的顺风下飞行 300 英里所需的时间相同。 飞机的速度是多少？

解决方案

这是一种统一的运动情况。 图表将帮助我们直观地了解情况。

我们填写图表来整理信息。

我们正在寻找飞机的速度。 让$r$ = 飞机的速度。

当飞机随风飞行时，风会提高其速度，速度也是如此$r + 30$。

当飞机逆风飞行时，风速会降低，速度降低$r − 30$。

写下费率。 在远处写字。 从那以后$D=r \cdot t$，我们求解$t$并得到$t=\dfrac{D}{r}$。 我们将距离除以每行的速率，然后将表达式放在时间列中。

	速率$\cdot$时间 = 距离
逆风	\ (\ cdot\) 时间 = 距离 “>$r-30$	$\dfrac{200}{r-30}$	200
顺风	\ (\ cdot\) 时间 = 距离 “>$r+30$	$\dfrac{300}{r+30}$	300

我们知道时间是相等的，所以我们写出方程式。

$$\dfrac{200}{r-30}=\dfrac{300}{r+30} \nonumber$$

我们将两边乘以液晶屏。

$$(r+30)(r-30)\left(\frac{200}{r-30}\right)=(r+30)(r-30)\left(\frac{300}{r+30}\right) \nonumber$$

简化并解决。

$$\begin{aligned} (r+30)(200)&=(r-30) 300 \\ 200 r+6000&=300 r-9000 \\ 15000&=100 r \end{aligned} \nonumber$$

查看。

飞$150 \mathrm{mph}$机的速度是合理的吗？ 是的。 如果飞机在行驶$150 \mathrm{mph}$而风在$30 \mathrm{mph}$行驶

$$\text { Tailwind } \quad 150+30=180 \mathrm{mph} \quad \dfrac{300}{180}=\dfrac{5}{3} \text { hours } \nonumber$$

$$\text { Headwind } 150-30=120 \mathrm{mph} \dfrac{200}{120}=\dfrac{5}{3} \text { hours } \nonumber$$

时间是相等的，所以它会检查。 飞机正在飞行$150 \mathrm{mph}$。

练习$\PageIndex{9}$

Link 可以在 3 英里/小时的逆风中骑自行车 20 英里，这与他以 3 英里/小时的顺风行驶 30 英里的时间相同。 Link 的骑行速度是多少？

回答

林克的骑行速度为 15 英里/小时。

练习$\PageIndex{10}$

Danica 可以在 7 英里/小时的逆风中航行 5 英里，这与她在 7 英里/小时的顺风下航行 12 英里的时间相同。 没有风的 Danica 的船速度是多少？

回答

丹妮卡的船的速度是 17 英里每小时。

在下一个示例中，我们将知道以不同速度行驶不同距离所产生的总时间。

示例$\PageIndex{6}$

周六，贾兹敏训练了 3 个小时。 她跑了 8 英里然后骑了 24 英里。 她的骑行速度比跑步速度快 4 英里/小时。 她的跑步速度是多少？

解决方案

这是一种统一的运动情况。 图表将帮助我们直观地了解情况。

我们填写图表来整理信息。 我们正在寻找 Jazmine 的跑步速度。 让$r$ = Jazmine 的跑步速度。

她的骑行速度比跑步速度快 4 英里。 $r + 4$= 她的骑行速度

给出了距离，将其输入到图表中。 从那以后$D=r \cdot t$，我们求解$t$并得到$t=\dfrac{D}{r}$。我们将距离除以每行的速率，然后将表达式放在时间列中。

	速率$\cdot$时间 = 距离
跑	\ (\ cdot\) 时间 = 距离 “>$r$	$\dfrac{8}{r}$	8
自行车	\ (\ cdot\) 时间 = 距离 “>$r+4$	$\dfrac{24}{r+4}$	24
	\ (\ cdot\) 时间 = 距离 “>	3

写一句话：她的时间加上骑自行车的时间是 3 小时。

翻译句子得出方程式。

$$\dfrac{8}{r}+\dfrac{24}{r+4}=3 \nonumber$$

解决。

\ [\ begin {aligned}
r (r+4)\ 左 (\ dfrac {8} {r} +\ dfrac {24} {r+4}\ 右) &=3\
cdot r (r+4)\ 24 r &=3 r (r+4)\\
8 r+32+24 r &=3 r^ {2} +12 r\
32+32 r &=3 r^ {2} +12 r\\
0 &=3 r^ {2} -20 r-32\\
0 & =( 3 r+4) (r-8)
\ end {aligned}\ nonumber\]

$$\begin{array}{lc} {(3 r+4)=0} & {(r-8)=0} \\ \cancel{r=\dfrac{4}{3}} \quad & {r=8} \end{array} \nonumber$$

查看。

在这个问题中，负速度是没有意义的，解决方案$r=8$也是如此。

8 英里/小时是合理的跑步速度吗？ 是的。

如果 Jazmine 的跑步速率为 4$r+4$，那么她的骑行速率就是$8+4=12$。

$$\text { Run } 8 \mathrm{mph} \quad \dfrac{8 \mathrm{miles}}{8 \mathrm{mph}}=1 \text { hour } \nonumber$$

$$\text { Bike } 12 \text { mph } \quad \dfrac{24 \text { miles }}{12 \mathrm{mph}}=2 \text { hours } \nonumber$$

总计 3 个小时。

Jazmine 的跑步速度为 8 英里/小时。

练习$\PageIndex{11}$

周六，丹尼斯进行了6个小时的越野滑雪。 他在上坡滑了20英里，然后向下滑了20英里，回到了起点。 他的上坡速度比下坡速度慢 5 英里/小时。 丹尼斯的上坡速度和下坡的速度是多少？

回答

丹尼斯的上坡速度为 10 英里/小时，下坡速度为 5 英里/小时。

练习$\PageIndex{12}$

Joon 开车4个小时回家，在州际公路上行驶208英里，在乡间小路上行驶40英里。 如果他在州际公路上的行驶速度比在乡间道路上快15英里/小时，那么他在乡间小路上的速度是多少？

回答

Joon 在乡间小路上的速度为 50 英里/小时。

再一次，我们将使用为变量求解的均匀运动公式$t$。

示例$\PageIndex{7}$

汉密尔顿骑着自行车沿着从家到大海的河道上下坡12英里，然后骑上坡回家。 他的上坡速度比下坡速度慢8英里/小时。 他回家的时间比他去海里花的时间长了两个小时。 找出汉密尔顿的下坡速度。

解决方案

这是一种统一的运动情况。 图表将帮助我们直观地了解情况。

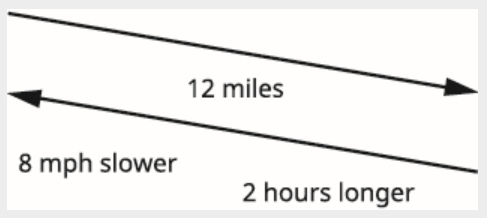
我们填写图表来整理信息。

我们正在寻找汉密尔顿的下坡速度。 让$h$ = 汉密尔顿的下坡速度。

他的上坡速度慢了每小时 8 英里。 $h-8$= 汉密尔顿的上坡速度。

在图表中输入汇率。

两个方向的距离相同：12 英里。

从那以后$D=r \cdot t$，我们求解$t$并得到$t=\dfrac{D}{r}$。 我们将距离除以每行的速率，然后将表达式放在时间列中。

	速率$\cdot$时间 = 距离
下坡	\ (\ cdot\) 时间 = 距离 “>$h$	$\dfrac{12}{h}$	12
上坡	\ (\ cdot\) 时间 = 距离 “>$h-8$	$\dfrac{12}{h-8}$	12

写一句关于这条线的一句话：他上坡的时间比下坡时间长 2 个小时。 上坡时间比下坡时间长 2。

翻译句子得出方程式。

$$\dfrac{12}{h-8}=\dfrac{12}{h}+2 \nonumber$$

解决。

\ [\ begin {aligned}
h (h-8)\ 左 (\ dfrac {12} {h-8}\ 右) &=h (h-8)\ 左 (\ dfrac {
12} {h} +2\ 右)\\ 12 h &=12 h (h-8)\\
12 h &=12 h^ {2} -16 h\\
0 &=2 h ^ {2} -16 h-96\\
0 &=2\ 左 (h^ {2} -8 h-48\ 右)\\
0 &=2 (h-12) (h+4)
\ end {aligned}\ nonumber\]

$$\begin{array}{lc} h-12=0 & h+4=0 \\ h=12 & \cancel {h=4} \end{array} \nonumber$$

查看。 下坡骑行是$12 \mathrm{mph}$合理的速度吗？ 是的。

$$\text { Downhill } 12 \mathrm{mph} \quad \dfrac{12 \text { miles }}{12 \mathrm{mph}}=1 \text { hour } \nonumber$$

$$\text { Uphill } 12-8=4 \mathrm{mph} \quad \dfrac{12 \text { miles }}{4 \mathrm{mph}}=3 \text { hours} \nonumber$$

上坡时间比下坡时间多 2 小时。

汉密尔顿的下坡速度是$12 \mathrm{mph}$.

练习$\PageIndex{13}$

一个周末，凯拉在离大学75英里的地方骑着自行车回家，然后乘公共汽车回大学。 她坐公交车回大学的时间比骑自行车回家花的时间少了两个小时，而且公交车的平均时速比凯拉的骑行速度快了10英里/小时。 查找 Kayla 的骑行速度。

回答

Kayla 的骑行速度为 15 英里/小时。

练习$\PageIndex{14}$

维多利亚沿着一条平坦的小径慢跑12英里到公园，然后在20英里的丘陵小径上慢跑返回。 她在丘陵小径上慢跑每小时比在平坦的小径上慢一英里，而且她的回程花了两个小时。 在平坦的小径上找到她的慢跑速度。

回答

维多利亚在平坦的小径上慢跑 6 英里/小时。

解决工作申请

每周八卦杂志有一篇关于公主宝贝的重大报道，编辑希望该杂志尽快出版。 她要求打印机额外运行一台印刷机以更快地完成打印。 按 #1 需要 6 个小时才能完成工作，按 #2 需要 12 个小时才能完成这项工作。 在两台印刷机一起运行的情况下，打印机需要多长时间才能打印杂志？

这是一个典型的 “工作” 应用程序。 这里涉及三个数量——两台印刷机单独完成工作所花费的时间，以及它们一起完成工作所花费的时间。

如果按 #1 可以在 6 小时内完成作业，那么它将在一小时$\dfrac{1}{6}$内完成作业。

如果按 #2 可以在 12 小时内完成作业，那么它将在一小时$\dfrac{1}{12}$内完成作业。

$t$我们将假设印刷机在两台印刷机一起运行的情况下印刷杂志所花费的小时数。 因此，在一起工作1小时后，他们就完成$\dfrac{1}{t}$了工作。

我们可以用 “方程” 一词对其进行建模，然后将其转换为有理方程。 为了找到印刷机协同工作需要多少时间才能完成工作，我们解决了问题$t$。

按照步骤整理信息。 我们正在寻找在两台印刷机一起运行的情况下完成这项工作需要多少小时。

第 1 步：让$t$ = 一起完成任务所需的小时数。

第 2 步：输入每项作业的工时，按 #1，按 #2，以及它们何时协同工作。

如果 Press #1 上的作业需要 6 个小时，则该作业将在 1 小时$\dfrac{1}{6}$内完成。

同样，可以找到 Press #2 的作业完成部分/小时以及两者何时在一起。

	完成任务的小时数。	部分作业已完成/小时
按 #1	6	$\dfrac{1}{6}$
按 #2	12	$\dfrac{1}{12}$
在一起	$t$	$\dfrac{1}{t}$

写一个单词句子。 按 #1 完成的部分加上 Press #2 完成的部分等于总完成的数量。

第 3 步：转换为方程式。

$$\text {Work completed by}\\ \underbrace{\text {Press } \#1 + \text {Press } \#2 = \text {Together}}\\ \dfrac{1}{6} \qquad+\qquad\dfrac{1}{12}\qquad =\qquad \dfrac{1}{t} \nonumber$$

第 4 步：求解。 简化。

$$\dfrac{1}{6}+\dfrac{1}{12}=\dfrac{1}{t} \nonumber$$

乘以 LCD，$12t$然后简化。

\ [\ begin {aligned}
12 t\ 左 (\ dfrac {1} {6} +\ dfrac {1} {12}\ 右) &=12 t\ 左 (\ dfrac {1} {t}\ 右)\\

2 t+t &=12\\
t &=4
\ end {aligner\]

当两台印刷机都在运行时，需要4个小时才能完成这项工作。

请记住，两台印刷机协同工作所需的时间应该比两台印刷机单独完成工作所需的时间要少。

示例$\PageIndex{8}$

假设 Pete 可以在 10 个小时内粉刷一个房间。 如果他以稳定的速度工作，他将在1小时内画出房间$\dfrac{1}{10}$的画面。 如果艾丽西亚要花 8 个小时来粉刷同一个房间，那么 1 小时后她就会画$\dfrac{1}{8}$出这个房间。 如果 Pete 和 Alicia 一起工作（并且不干扰彼此的进步），他们要花多长时间才能粉刷房间？

解决方案

这是一个 “工作” 应用程序。 以下步骤将帮助我们整理信息。 我们正在寻找他们一起粉刷房间所需的小时数。

一小时后 Pete 就完成$\dfrac{1}{10}$了这份工作。 艾丽西亚做$\dfrac{1}{8}$了这份工作。 他们一起完成$\dfrac{1}{t}$了这项工作。

第 1 步：假设$t$一起粉刷房间所需的小时数。

第 2 步：输入 Pete、Alicia 每份工作的工时以及他们在一起工作的时间。 他们一起工作了 1 个小时，就完成$\dfrac{1}{t}$了工作。 同样，找到 Pete 和 Alicia 完成的工作每小时完成的那部分。

	完成任务的小时数。	部分作业已完成/小时
彼得	10	$\dfrac{1}{10}$
艾丽西亚	8	$\dfrac{1}{8}$
在一起	$t$	$\dfrac{1}{t}$

写一个单词句子。 Pete 完成的工作加上 Alicia 完成的工作等于已完成的工作总数。

第 3 步：转换为方程式。

$$\text {Work completed by}\\ \underbrace{\text {Pete } + \text {Alicia } = \text {Together}}\\ \dfrac{1}{10} \qquad+\qquad\dfrac{1}{8}\qquad =\qquad \dfrac{1}{t} \nonumber$$

步骤 4：简化。 解决。

乘以液晶屏，$40t$。

$$40 t\left(\dfrac{1}{10}+\dfrac{1}{8}\right)=40 t\left(\dfrac{1}{t}\right) \nonumber$$

分发。

$$40 t \cdot \dfrac{1}{10}+40 t \cdot \dfrac{1}{8}=40 t\left(\dfrac{1}{t}\right) \nonumber$$

简化并解决。

\ [\ begin {array}
{r} {4 t+5 t=40}\\
{9 t=40}\\
{t=\ dfrac {40} {9}}
\ end {array}\ nonumber\]

我们将写成混合数字，这样我们就可以将其转换为小时和分钟。

$$t=4 \dfrac{4}{9} \text { hours } \nonumber$$

请记住，1 小时 = 60 分钟。

$$t=4 \text { hours }+\dfrac{4}{9}(60 \text { minutes }) \nonumber$$

乘以，然后四舍五入到最接近的分钟。

$$t=4 \text { hours }+27\text { minutes } \nonumber$$

Pete 和 Alica 要花大约 4 小时 27 分钟才能粉刷房间。

练习$\PageIndex{15}$

一个园丁可以在 4 小时内修剪一个高尔夫球场，而另一个园丁可以在 6 小时内修剪同一个高尔夫球场。 如果两个园丁一起修剪高尔夫球场需要多长时间？

回答

当两个园丁一起工作时，需要2小时24分钟。

练习$\PageIndex{16}$

达里亚可以在7个小时内在花园里除草，而她的母亲可以在3个小时内除草。 他们两个一起工作要花多长时间？

回答

当 Daria 和她的母亲一起工作时，需要 2 小时 6 分钟。

示例$\PageIndex{9}$

Ra'shon 可以在 7 小时内打扫房子。 当他的妹妹帮助他时，需要3个小时。 他妹妹独自打扫房子要花多长时间？

解决方案

这是一个工作问题。 以下步骤将帮助我们整理信息。 我们正在寻找 Ra'shon 的姐姐要花多少小时才能独自完成这项工作。

第 1 步：假$s$设 Ra'shon 的姐姐独自打扫房子所花的小时数。

第 2 步：输入他的妹妹 Ra'shon 每份工作的工时，以及他们在一起工作的时间。 如果 Ra'shon 需要 7 个小时，则在 1 小时内$\dfrac{1}{s}$完成作业。 如果 Ra'shon 的姐姐花了$s$几个小时，那么工作在 1 小时$\dfrac{1}{s}$内就完成了。

	完成任务的小时数。	部分作业已完成/小时
Ra'shon	7	$\dfrac{1}{7}$
他的妹妹	$s$	$\dfrac{1}{s}$
在一起	3	$\dfrac{1}{3}$

写一个单词句子。 Ra'shon 完成的部分加上他姐姐完成的部分等于总共完成的金额。

步骤 3：转换为方程。

$$\text {Work completed by}\\ \underbrace{\text {Ra'shon } + \text {His sister } = \text {Together}}\\ \dfrac{1}{7} \qquad+\qquad\dfrac{1}{s}\qquad =\qquad \dfrac{1}{3} \nonumber$$

步骤 4：简化。 解决。

$$\dfrac{1}{7}+\dfrac{1}{5}=\dfrac{1}{3} \nonumber$$

乘以液晶显示屏 21 秒。

\ [\ begin {aligned}
21 s\ 左 (\ dfrac {1} {7} +\ dfrac {1} {s}\ 右) &=\ 左 (\ dfrac {1} {3}\ 右) 21 s\\\
3 s+21 &=7 s\ end {alig
ned}\ nonumber\]

简化。

\ [\ begin {aligned}-
4 s &=-21\\
s &=\ frac {-21} {-4} =\ frac {21} {4}
\ end {aligned}\ nonumber\]

以混合数字写入，将其转换为小时和分钟。

$$s=5 \dfrac{1}{4} \text { hours } \nonumber$$

1 小时内有 60 分钟。

$$s=5 \text { hours }+\dfrac{1}{4}(60 \text { minutes })\\ s=5\text { hours }+15\text { minutes } \nonumber$$

Ra'shon 的姐姐要花 5 小时 15 分钟才能独自打扫房子。

练习$\PageIndex{17}$

爱丽丝可以在 6 小时内粉刷一个房间。 如果克里斯蒂娜帮助她，他们要花4个小时才能粉刷房间。 克里斯蒂娜自己粉刷房间要花多长时间？

回答

克里斯蒂娜可以在 12 小时内粉刷房间。

练习$\PageIndex{18}$

Tracy 可以在 3 小时内铺设一块混凝土板，在乔丹的帮助下，他们可以在 2 小时内完成。 如果乔丹独自工作，需要多长时间？

回答

这将需要乔丹6个小时。

解决直接变异问题

当两个量按比例关联时，我们说它们彼此成正比。 表达这种关系的另一种方法是讨论两个数量的变化。 在本节中，我们将讨论直接变异和逆变异。

Lindsay 在工作时每小时可获得 15 美元的报酬。 如果我们$s$把她的薪水当作她的工作时数，我们可以用方程式来模拟这种情况

$$s=15 h \nonumber$$

Lindsay 的薪水是常数 15 和她工作时数的乘积。 我们说林赛的薪水与她的工作时数直接不同。 如果一个变量是常量的乘积，而另一个变量是直接变化。

直接变体

对于任意两个变量$x$ and$y$，与$x$ if 直接$y$变化

$y=kx$，哪里$k\neq 0$

该常数$k$被称为变异常数。

在使用直接变异的应用程序中，通常我们会知道一对变量的值，并被要求找到$x$与相关的方程$y$。 然后我们可以使用该方程来查找其他值的值$x$。$y$

我们将在此处列出步骤。

如何解决直接变异问题

第 1 步。 写出直接变异的公式。

第 2 步。 用给定值代替变量。

第 3 步。 求解变异常数。

第 4 步。 写出相关方程$x$并$y$使用变异常数。

现在我们将求解直接变异的应用。

示例$\PageIndex{10}$

当拉乌尔在健身房的跑步机上跑步时$c$，他消耗的卡路里数量直接随分钟数变化$m$，他使用跑步机。 当他使用跑步机 18 分钟时，他消耗了 315 卡路里的热量。

1. 写下与$c$和相关的方程式$m$。
2. 如果他在跑步机上跑了 25 分钟，他会消耗多少卡路里？

解决方案

卡路里的数量直接取决于跑步机上的分钟数$m$、跑步机上的卡路里数和$c=315$时间$m=18$。$c$

写出直接变异的公式。

$$y=kx \nonumber$$

我们将使用$c$来代替$y$和$m$代替$x$。

$$c=k m \nonumber$$

用给定值代替变量。

$$315=k \cdot 18 \nonumber$$

求解变异常数。

\ [\ begin {aligned}
&\ dfrac {315} {18} =\ dfrac {k\ cdot 18} {18}\\\
&17.5=k
\ end {aligned}\ nonumber\]

写下与$c$和相关的方程式$m$。

$$c=k m \nonumber$$

用变异常数代替。

$$c=17.5 m \nonumber$$

找出$c$时间$m = 25$。

写下与$c$和相关的方程式$m$。

$$c=17.5 m \nonumber$$

用给定的值替换$m$。

$$c=17.5(25) \nonumber$$

简化。

$$c=437.5 \nonumber$$

如果拉乌尔使用跑步机 25 分钟，他将消耗 437.5 卡路里的热量。

练习$\PageIndex{19}$

消耗的卡$c$路里数量直接随运动所花费的时间$t$而变化。 阿诺德在 65 分钟的锻炼中消耗了 312 卡路里的热量。

1. 写下与$c$和相关的方程式$t$。
2. 如果他运动 90 分钟，他会消耗多少卡路里？

回答

1. $c=4.8 t$
2. 他会消耗 432 卡路里的热量。

练习$\PageIndex{20}$

移动物体行进的距离$d$，随着时间的推移直接变化$t$，它会移动。 一列火车在 2 小时内行驶 100 英里。

1. 写下与$d$和相关的方程式$t$。
2. 它会在 5 小时内行驶多少英里？

回答

1. $d=50 t$
2. 它会行驶 250 英里。

解决逆变问题

许多应用程序涉及两个反向变化的变量。 随着一个变量的增加，另一个变量的减少。 将它们关联的方程式是$y=\dfrac{k}{x}$。

反向变化

对于任意两个变量 an$x$ d$y$，与$x$ if 成反比$y$变化

$y=\dfrac{k}{x}$，哪里$k\neq 0$

该常数$k$被称为变异常数。

逆@@ 变中的 “逆变” 一词是指乘法逆变。 的乘法逆$x$为$\dfrac{1}{x}$。

我们解决逆变异问题的方式与解决直接变异问题的方法相同。 只有方程的一般形式发生了变化。 我们将在这里复制程序框，然后将 “直接” 更改为 “反向”。

如何解决逆变问题

第 1 步。 写下逆变异的公式。

第 2 步。 用给定值代替变量。

第 3 步。 求解变异常数。

第 4 步。 写出相关方程$x$并$y$使用变异常数。

示例$\PageIndex{11}$

吉他弦的频率与其长度成反比。 一个 26 英寸 -长弦的振动频率为每秒 440 次。

1. 写下变异方程。
2. 如果将手指放在琴格上将琴弦的长度缩短到 20 英寸，每秒会有多少振动？

解决方案

频率与长度成反比。

为变量命名。 让$f$ = 频率。 $L$= 长度

写下逆变异的公式。

$$y=\dfrac{k}{x} \nonumber$$

我们将使用$f$来代替$y$和$L$代替$x$。

$$f=\dfrac{k}{L} \nonumber$$

$$f=440 \text { when } L=26 \nonumber$$

用给定值代替变量。

$$440=\dfrac{k}{26} \nonumber$$

求解变异常数。

\ [\ begin {aligned}
&26 (440) =26\ 左 (\ dfrac {k} {26}\ 右)\\
&11,440=k
\ end {aligned}\ nonumber\]

写下与$f$和相关的方程式$L$。

$$f=\dfrac{k}{L} \nonumber$$

用变异常数代替。

$$f=\dfrac{11,440}{L} \nonumber$$

找出$f$时间$L=20$。

写下与$f$和相关的方程式$L$。

$$f=\dfrac{11,440}{L} \nonumber$$

用给定值替换 L。

$$f=\dfrac{11,440}{20} \nonumber$$

简化。

$$f=572 \nonumber$$

一根 20 英寸的吉他弦每秒振动 572 次。

练习$\PageIndex{21}$

冰融化所需的小时数与空气温度成反比。 假设温度为 65 摄氏度时，一块冰在 2 小时内融化。

1. 写下变异方程。
2. 如果温度为78度，同一块冰需要多少小时才能融化？

回答

1. $h=\dfrac{130}{t}$
2. $1 \dfrac{2}{3}$小时

练习$\PageIndex{22}$

Xander的新业务发现，对其产品的每日需求与价格成反比$p$。 当价格为5美元时，需求为700个单位。

1. 写下变异方程。
2. 如果价格提高到7美元，需求是多少？

回答

1. $x=\dfrac{3500}{p}$
2. 500 个单位

媒体访问其他在线资源

访问此在线资源，获取有关有理表达式应用的更多指导和练习

• 有理表达式的应用