7.3E：练习

练习成就完美

用公分母加减有理表达式

在以下练习中，添加。

1。 \(\dfrac{2}{15}+\dfrac{7}{15}\)

回答

\(\dfrac{3}{5}\)

2。 \(\dfrac{7}{24}+\dfrac{11}{24}\)

3。 \(\dfrac{3c}{4c−5}+\dfrac{5}{4c−5}\)

回答

\(\dfrac{3c+5}{4c−5}\)

4。 \(\dfrac{7m}{2m+n}+\dfrac{4}{2m+n}\)

5。 \(\dfrac{2r^2}{2r−1}+\dfrac{15r−8}{2r−1}\)

回答

\(r+8\)

6。 \(\dfrac{3s^2}{3s−2}+\dfrac{13s−10}{3s−2}\)

7。 \(\dfrac{2w^2}{w^2−16}+\dfrac{8w}{w^2−16}\)

回答

\(\dfrac{2w}{w−4}\)

8。 \(\dfrac{7x^2}{x^2−9}+\dfrac{21x}{x^2−9}\)

在以下练习中，减去。

9。 \(\dfrac{9a^2}{3a−7}−\dfrac{49}{3a−7}\)

回答

\(3a+7\)

10。 \(\dfrac{25b^2}{5b−6}−\dfrac{36}{5b−6}\)

11。 \(\dfrac{3m^2}{6m−30}−\dfrac{21m−30}{6m−30}\)

回答

\(\dfrac{m−2}{2}\)

12。 \(\dfrac{2n^2}{4n−32}−\dfrac{18n−16}{4n−32}\)

13。 \(\dfrac{6p^2+3p+4}{p^2+4p−5}−\dfrac{5p^2+p+7}{p^2+4p−5}\)

回答

\(\dfrac{p+3}{p+5}\)

14。 \(\dfrac{5q^2+3q−9}{q^2+6q+8}−\dfrac{4q^2+9q+7}{q^2+6q+8}\)

15。 \(\dfrac{5r^2+7r−33}{r^2−49}−\dfrac{4r^2+5r+30}{r^2−49}\)

回答

\(\dfrac{r+9}{r+7}\)

16。 \(\dfrac{7t^2−t−4}{t^2−25}−\dfrac{6t^2+12t−44}{t^2−25}\)

加减分母对立的有理表达式

在以下练习中，加上或减去。

17。 \(\dfrac{10v}{2v−1}+\dfrac{2v+4}{1−2v}\)

回答

\(4\)

18。 \(\dfrac{20w}{5w−2}+\dfrac{5w+6}{2−5w}\)

19。 \(\dfrac{10x^2+16x−7}{8x−3}+\dfrac{2x^2+3x−1}{3−8x}\)

回答

\(x+2\)

20。 \(\dfrac{6y^2+2y−11}{3y−7}+\dfrac{3y^2−3y+17}{7−3y}\)

21。 \(\dfrac{z^2+6z}{z^2−25}−\dfrac{3z+20}{25−z^2}\)

回答

\(\dfrac{z+4}{z−5}\)

22。 \(\dfrac{a^2+3a}{a^2−9}−\dfrac{3a−27}{9−a^2}\)

23。 \(\dfrac{2b^2+30b−13}{b^2−49}−\dfrac{2b^2−5b−8}{49−b^2}\)

回答

\(\dfrac{4b−3}{b−7}\)

24。 \(\dfrac{c^2+5c−10}{c^2−16}−\dfrac{c^2−8c−10}{16−c^2}\)

找出有理表达式的最小公分母

在以下练习中，a. 找到给定有理表达式的 LCD b. 将它们重写为公分母最小的等效有理表达式。

25。 \(\dfrac{5}{x^2−2x−8},\dfrac{2x}{x^2−x−12}\)

回答

a.\((x+2)(x−4)(x+3)\)
b.\(\dfrac{5x+15}{(x+2)(x−4)(x+3)}\)，
\(\dfrac{2x^2+4x}{(x+2)(x−4)(x+3)}\)

26。 \(\dfrac{8}{y^2+12y+35},\dfrac{3y}{y^2+y−42}\)

27。 \(\dfrac{9}{z^2+2z−8},\dfrac{4z}{z^2−4}\)

回答

a.\((z−2)(z+4)(z−4)\)
b.\(\dfrac{9z−36}{(z−2)(z+4)(z−4)}\)，
\(\dfrac{4z^2−8z}{(z−2)(z+4)(z−4)}\)

28。 \(\dfrac{6}{a^2+14a+45},\dfrac{5a}{a^2−81}\)

29。 \(\dfrac{4}{b^2+6b+9},\dfrac{2b}{b^2−2b−15}\)

回答

a.\((b+3)(b+3)(b−5)\)
b.\(\dfrac{4b−20}{(b+3)(b+3)(b−5)}\)，
\(\dfrac{2b^2+6b}{(b+3)(b+3)(b−5)}\)

30。 \(\dfrac{5}{c^2−4c+4},\dfrac{3c}{c^2−7c+10}\)

31。 \(\dfrac{2}{3d^2+14d−5},\dfrac{5d}{3d^2−19d+6}\)

回答

a.\((d+5)(3d−1)(d−6)\)
b.\(\dfrac{2d−12}{(d+5)(3d−1)(d−6)}\)，
\(\dfrac{5d^2+25d}{(d+5)(3d−1)(d−6)}\)

32。 \(\dfrac{3}{5m^2−3m−2},\dfrac{6m}{5m^2+17m+6}\)

使用不同分母加减有理表达式

在以下练习中，执行指定的操作。

33。 \(\dfrac{7}{10x^2y}+\dfrac{4}{15xy^2}\)

回答

\(\dfrac{21y+8x}{30x^2y^2}\)

34。 \(\dfrac{1}{12a^3b^2}+\dfrac{5}{9a^2b^3}\)

35。 \(\dfrac{3}{r+4}+\dfrac{2}{r−5}\)

回答

\(\dfrac{5r−7}{(r+4)(r−5)}\)

36。 \(\dfrac{4}{s−7}+\dfrac{5}{s+3}\)

37。 \(\dfrac{5}{3w−2}+\dfrac{2}{w+1}\)

回答

\(\dfrac{11w+1}{(3w−2)(w+1)}\)

38。 \(\dfrac{4}{2x+5}+\dfrac{2}{x−1}\)

39。 \(\dfrac{2y}{y+3}+\dfrac{3}{y−1}\)

回答

\(\dfrac{2y^2+y+9}{(y+3)(y−1)}\)

40。 \(\dfrac{3z}{z−2}+\dfrac{1}{z+5}\)

41。 \(\dfrac{5b}{a^2b−2a^2}+\dfrac{2b}{b^2−4}\)

回答

\(\dfrac{b(5b+10+2a^2)}{a^2(b−2)(b+2)}\)

42。 \(\dfrac{4}{cd+3c}+\dfrac{1}{d^2−9}\)

43。 \(\dfrac{−3m}{3m−3}+\dfrac{5m}{m^2+3m−4}\)

回答

\(-\dfrac{m}{m+4}\)

44。 \(\dfrac{8}{4n+4}+\dfrac{6}{n^2−n−2}\)

45。 \(\dfrac{3r}{r^2+7r+6}+\dfrac{9}{r^2+4r+3}\)

回答

\(\dfrac{3(r^2+6r+18)}{(r+1)(r+6)(r+3)}\)

46。 \(\dfrac{2s}{s^2+2s−8}+\dfrac{4}{s^2+3s−10}\)

47。 \(\dfrac{t}{t−6}−\dfrac{t−2}{t+6}\)

回答

\(\dfrac{2(7t−6)}{(t−6)(t+6)}\)

48。 \(\dfrac{x−3}{x+6}−\dfrac{x}{x+3}\)

49。 \(\dfrac{5a}{a+3}−\dfrac{a+2}{a+6}\)

回答

\(\dfrac{4a^2+25a−6}{(a+3)(a+6)}\)

50。 \(\dfrac{3b}{b−2}−\dfrac{b−6}{b−8}\)

51。 \(\dfrac{6}{m+6}−\dfrac{12m}{m^2−36}\)

回答

\(\dfrac{−6}{m−6}\)

52。 \(\dfrac{4}{n+4}−\dfrac{8n}{n^2−16}\)

53。 \(\dfrac{−9p−17}{p^2−4p−21}−\dfrac{p+1}{7−p}\)

回答

\(\dfrac{p+2}{p+3}\)

54。 \(\dfrac{−13q−8}{q^2+2q−24}−\dfrac{q+2}{4−q}\)

55。 \(\dfrac{−2r−16}{r^2+6r−16}−\dfrac{5}{2−r}\)

回答

\(\dfrac{3}{r−2}\)

56。 \(\dfrac{2t−30}{t^2+6t−27}−\dfrac{2}{3−t}\)

57。 \(\dfrac{2x+7}{10x−1}+3\)

回答

\(\dfrac{4(8x+1)}{10x−1}\)

58。 \(\dfrac{8y−4}{5y+2}−6\)

59。 \(\dfrac{3}{x^2−3x−4}−\dfrac{2}{x^2−5x+4}\)

回答

\(\dfrac{x−5}{(x−4)(x+1)(x−1)}\)

60。 \(\dfrac{4}{x^2−6x+5}−\dfrac{3}{x^2−7x+10}\)

61。 \(\dfrac{5}{x^2+8x−9}−\dfrac{4}{x^2+10x+9}\)

回答

\(\dfrac{1}{(x−1)(x+1)}\)

62。 \(\dfrac{3}{2x^2+5x+2}−\dfrac{1}{2x^2+3x+1}\)

63。 \(\dfrac{5a}{a−2}+\dfrac{9}{a}−\dfrac{2a+18}{a^2−2a}\)

回答

\(\dfrac{5a^2+7a−36}{a(a−2)}\)

64。 \(\dfrac{2b}{b−5}+\dfrac{3}{2b}−\dfrac{2b−15}{2b^2−10b}\)

65。 \(\dfrac{c}{c+2}+\dfrac{5}{c−2}−\dfrac{10c}{c^2−4}\)

回答

\(\dfrac{c−5}{c+2}\)

66。 \(\dfrac{6d}{d−5}+\dfrac{1}{d+4}+\dfrac{7d−5}{d^2−d−20}\)

67。 \(\dfrac{3d}{d+2}+\dfrac{4}{d}−\dfrac{d+8}{d^2+2d}\)

回答

\(\dfrac{3(d+1)}{d+2}\)

68。 \(\dfrac{2q}{q+5}+\dfrac{3}{q−3}−\dfrac{13q+15}{q^2+2q−15}\)

加减有理函数

在以下练习中，找到 a.\(R(x)=f(x)+g(x)\) b\(R(x)=f(x)−g(x)\).

69。 \(f(x)=\dfrac{−5x−5}{x^2+x−6}\)和\( g(x)=\dfrac{x+1}{2−x}\)

回答

a.\(R(x)=−\dfrac{(x+8)(x+1)}{(x−2)(x+3)}\)
b。\(R(x)=\dfrac{x+1}{x+3}\)

70。 \(f(x)=\dfrac{−4x−24}{x^2+x−30}\)和\( g(x)=\dfrac{x+7}{5−x}\)

71。 \(f(x)=\dfrac{6x}{x^2−64}\)和\(g(x)=\dfrac{3}{x−8}\)

回答

a.\(R(x)=\dfrac{3(3x+8)}{(x−8)(x+8)}\)
b。\(R(x)=\dfrac{3}{x+8}\)

72。 \(f(x)=\dfrac{5}{x+7}\)和\( g(x)=\dfrac{10x}{x^2−49}\)

写作练习

73。 唐纳德认为\(\dfrac{3}{x}+\dfrac{4}{x}\)是这样\(\dfrac{7}{2x}\)。 唐纳德对吗？ 解释一下。

回答

答案会有所不同。

74。 解释如何找到\(x^2+5x+4\)和的最小公分母\(x^2−16\)。

75。 费利佩认为\(\dfrac{1}{x}+\dfrac{1}{y}\)是\(\dfrac{2}{x+y}\)。
a. 为 x 和 y 选择数值并进行计算\(\dfrac{1}{x}+\dfrac{1}{y}\)。
b. 计算\(\dfrac{2}{x+y}\)与 a 部分中使用的 x 和 y 的值相同。
c. 解释为什么 Felipe 错了。
d. 找到正确的表达式\(1x+1y\)。

回答

a. 答案会有所不同。
b. 答案视情况而定。
c. 答案视情况而定。
d。\(\dfrac{x+y}{x}\)

76。 简化表达式\(\dfrac{4}{n^2+6n+9}−\dfrac{1}{n^2−9}\)并解释所有步骤。

自检

a. 完成练习后，使用此清单评估您对本节目标的掌握程度。

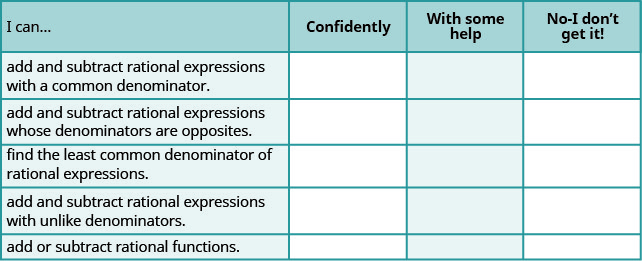
b. 看完这份清单后，你会怎么做才能对所有目标充满信心？