7.3:加减有理表达式
- Page ID
- 204233
在本节结束时,您将能够:
- 用公分母加减有理表达式
- 加减分母相反的有理表达式
- 找出有理表达式的最小公分母
- 添加和减去具有不同分母的有理表达式
- 加减有理函数
在@@
用公分母加减有理表达式
当你添加数值分数时,你要做的第一步是什么? 你检查它们是否有共同点。 如果有,则将分子相加,然后将总和放在公分母之上。 如果它们没有公分母,则在添加之前先找到一个公分母。
有理表达式也是如此。 要添加有理表达式,它们必须有一个共同的分母。 当分母相同时,将分子相加,然后将总和置于公分母之上。
如果\(p\)\(q\)、和\(r\)是多项式\(r\neq 0\),其中,那么
\[\dfrac{p}{r}+\dfrac{q}{r}=\dfrac{p+q}{r} \quad \text{and} \quad \dfrac{p}{r}−\dfrac{q}{r}=\dfrac{p−q}{r}\nonumber\]
要加上或减去具有公分母的有理表达式,请将分子相加或减去,然后将结果置于公分母之上。
我们总是简化有理表达。 如果可能的话,一定要在减去分子之后进行分数,这样你就可以识别出任何常见的因子。
还要记住,我们不允许使用会使分母为零的值。 在下一个示例中\(x\)应排除的哪个值?
添加:\(\dfrac{11x+28}{x+4}+\dfrac{x^2}{x+4}\)。
解决方案
由于分母是\(x+4\),我们必须排除该值\(x=−4\)。
\(\begin{array} {ll} &\dfrac{11x+28}{x+4}+\dfrac{x^2}{x+4},\space x\neq −4 \\ \begin{array} {l} \text{The fractions have a common denominator,} \\ \text{so add the numerators and place the sum} \\ \text{over the common denominator.} \end{array} &\dfrac{11x+28+x^2}{x+4} \\ & \\ \text{Write the degrees in descending order.} &\dfrac{x^2+11x+28}{x+4} \\ & \\ \text{Factor the numerator.} &\dfrac{(x+4)(x+7)}{x+4} \\ & \\ \text{Simplify by removing common factors.} &\dfrac{\cancel{(x+4)}(x+7)}{\cancel{x+4}} \\ & \\ \text{Simplify.} &x+7 \end{array}\)
表达式简化为,\(x+7\)但原始表达式的分母为 s\(x+4\) o\(x\neq −4\)。
简化:\(\dfrac{9x+14}{x+7}+\dfrac{x^2}{x+7}\)。
- 回答
-
\(x+2\)
简化:\(\dfrac{x^2+8x}{x+5}+\dfrac{15}{x+5}\)。
- 回答
-
\(x+3\)
要减去有理表达式,它们还必须有一个共同的分母。 当分母相同时,可以减去分子,然后将差值放在公分母上。 减去二项式或三项式时要注意这些符号。
减去:\(\dfrac{5x^2−7x+3}{x^2−3x+18}−\dfrac{4x^2+x−9}{x^2−3x+18}\)。
解决方案
\(\begin{array} {ll} &\dfrac{5x^2−7x+3}{x^2−3x+18}−\dfrac{4x^2+x−9}{x^2−3x+18} \\ & \\ \begin{array} {l} \text{Subtract the numerators and place the} \\ \text{difference over the common denominator.} \end{array} &\dfrac{5x^2−7x+3−(4x^2+x−9)}{x^2−3x+18} \\ & \\ \text{Distribute the sign in the numerator.} &\dfrac{5x^2−7x+3−4x^2−x+9}{x^2−3x−18} \\ & \\ \text{Combine like terms.} &\dfrac{x^2−8x+12}{x^2−3x−18} \\ & \\ \text{Factor the numerator and the denominator.} &\dfrac{(x−2)(x−6)}{(x+3)(x−6)} \\ & \\ \text{Simplify by removing common factors.} &\dfrac{(x−2)\cancel{(x−6)}}{(x+3)\cancel{(x−6)}} \\ & \\ &(x−2)(x+3) \end{array}\)
减去:\(\dfrac{4x^2−11x+8}{x^2−3x+2}−\dfrac{3x^2+x−3}{x^2−3x+2}\)。
- 回答
-
\(\dfrac{x−11}{x−2}\)
减去:\(\dfrac{6x^2−x+20}{x^2−81}−\dfrac{5x^2+11x−7}{x^2−81}\)。
- 回答
-
\(\dfrac{x−3}{x+9}\)
加减分母对立的有理表达式
当两个有理表达式的分母相反时,很容易得到一个共同的分母。 我们只需要将其中一个分数乘以\(\dfrac{−1}{−1}\)。
让我们看看这是如何工作的。
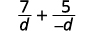 |
|
| 将第二个分数乘以\(\dfrac{−1}{−1}\)。 | 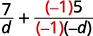 |
| 分母是一样的。 | 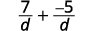 |
| 简化。 | 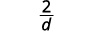 |
在减去分数时,在处理对立面时要小心符号。
减去:\(\dfrac{m^2−6m}{m^2−1}−\dfrac{3m+2}{1−m^2}\)。
解决方案
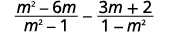 |
|
|
分母是相反的,因此将 |
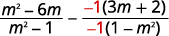 |
| 简化第二部分。 | 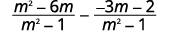 |
| 分母是一样的。 减去分子。 | 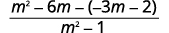 |
| 分发。 | 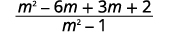 |
| 将相似的术语组合在一起。 | 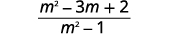 |
| 系数分子和分母。 | 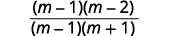 |
| 通过删除常见因素进行简化。 | 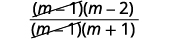 |
| 简化。 | 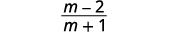 |
减去:\(\dfrac{y^2−5y}{y^2−4}−\dfrac{6y−6}{4−y^2}\)。
- 回答
-
\(\dfrac{y+3}{y+2}\)
减去:\(\dfrac{2n^2+8n−1}{n^2−1}−\dfrac{n^2−7n−1}{1−n^2}\)。
- 回答
-
\(\dfrac{3n−2}{n−1}\)
找出有理表达式的最小公分母
当我们加上或减去具有不同分母的有理表达式时,我们需要得到公分母。 如果我们回顾一下我们使用数字分数的程序,我们就会知道如何处理有理表达式。
让我们来看这个例子:\(\dfrac{7}{12}+\dfrac{5}{18}\). 由于分母不同,第一步是找到最小公分母 (LCD)。
为了找到分数的液晶显示器,我们将12和18分解为素数,将所有常见的素数排成列在列中。 然后我们从每列中 “降低” 一个素数。 最后,我们将这些因子相乘得出液晶屏。
当我们添加数值分数时,一旦找到液晶显示屏,我们通过将分子和分母乘以相同的数字,将每个分数重写为与液晶显示屏的等效分数。 我们现在准备添加。
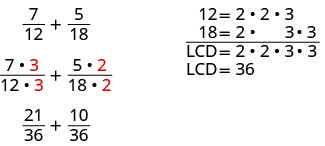
对于理性表达,我们也做同样的事情。 但是,我们将液晶屏保留为保值形式。
- 将每个分母完全考虑在内。
- 列出每个分母的因子。 尽可能垂直匹配因子。
- 通过包含所有因子来缩小各列,但不要将常见因子包含两次。
- 将液晶屏写成因素的乘积。
请记住,我们总是排除会使分母为零的值。 在下一个示例中,我们应该排除 xx 的哪些值?
a. 找到表达式的 LCD\(\dfrac{8}{x^2−2x−3}\)\(\dfrac{3x}{x^2+4x+3}\),然后 b. 将它们重写为公分母最小的等效有理表达式。
解决方案
一个。
| 找到\(\dfrac{8}{x^2−2x−3}\),的液晶屏\(\dfrac{3x}{x^2+4x+3}\)。 | |
| 将每个分母完全考虑在内,列出共同的因素。 把柱子放下。 |
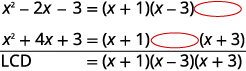 |
| 将液晶屏写成因素的乘积。 | 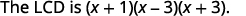 |
b。
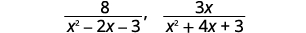 |
|
| 将每个分母除去。 | 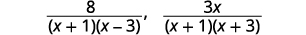 |
| 将每个分母乘以 “缺失” 的 LCD 系数,然后将每个分子乘以相同的系数。 |
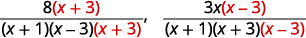 |
| 简化分子。 | 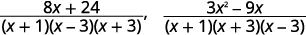 |
a. 找到表达式的 LCD\(\dfrac{2}{x^2−x−12}\),\(\dfrac{1}{x^2−16}\)b. 将它们重写为公分母最小的等效有理表达式。
- 回答
-
a.\((x−4)(x+3)(x+4)\)
b.\(\dfrac{2x+8}{(x−4)(x+3)(x+4)}\),
\(\dfrac{x+3}{(x−4)(x+3)(x+4)}\)
a. 找到表达式的 LCD\(\dfrac{3x}{x^2−3x+10}\),\(\dfrac{5}{x^2+3x+2}\)b. 将它们重写为公分母最小的等效有理表达式。
- 回答
-
a.\((x+2)(x−5)(x+1)\)
b.\(\dfrac{3x^2+3x}{(x+2)(x−5)(x+1)}\),
\(\dfrac{5x−25}{(x+2)(x−5)(x+1)}\)
使用不同分母加减有理表达式
现在我们有了添加或减去具有不同分母的有理表达式所需的所有步骤。
添加:\(\dfrac{3}{x−3}+\dfrac{2}{x−2}\)。
解决方案



添加:\(\dfrac{2}{x−2}+\dfrac{5}{x+3}\)。
- 回答
-
\(\dfrac{7x−4}{(x−2)(x+3)}\)
添加:\(\dfrac{4}{m+3}+\dfrac{3}{m+4}\)。
- 回答
-
\(\dfrac{7m+25}{(m+3)(m+4)}\)
此处总结了用于添加有理表达式的步骤。
- 确定表达式是否有公分母。
- 是-转到步骤 2。
- 否 — 使用 LCD 重写每个有理表达式。
- 找到液晶屏。
- 使用 LCD 将每个有理表达式重写为等效的有理表达式。
- 加上或减去有理表达式。
- 尽可能简化。
避免过早简化的诱惑。 在上面的例子中,我们必须保留第一个有理表达式\(\dfrac{3x−6}{(x−3)(x−2)}\)才能将其添加到\(\dfrac{2x−6}{(x−2)(x−3)}\)。 只有在组合分子后才能简化。
添加:\(\dfrac{8}{x^2−2x−3}+\dfrac{3x}{x^2+4x+3}\)。
解决方案
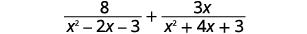 |
|
| 这些表达式有共同点吗? | 不。 |
| 使用 LCD 重写每个表达式。 | |
| \(\begin{array} {ll} & \\ & \\ \text{Find the LCD.} &\begin{array} {l} \hspace{5mm} x^2−2x−3=(x+1)(x−3) \\ \underline{x^2+4x+3=(x+1)\quad (x+3)} \\ & \\ \qquad LCD=(x+1)(x−3)(x+3) \end{array} \end{array} \) | |
| 使用 LCD 将每个有理表达式重写为 等效的有理表达式。 |
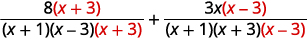 |
| 简化分子。 | 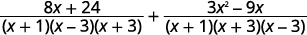 |
| 添加有理表达式。 | 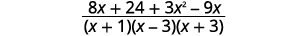 |
| 简化分子。 | 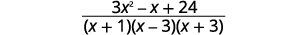 |
| 分子是素数,因此 没有常见的因子。 |
添加:\(\dfrac{1}{m^2−m−2}+\dfrac{5m}{m^2+3m+2}\)。
- 回答
-
\(\dfrac{5m^2−9m+2}{(m+1)(m−2)(m+2)}\)
添加:\(\dfrac{2n}{n^2−3n−10}+\dfrac{6}{n^2+5n+6}\)。
- 回答
-
\(\dfrac{2n^2+12n−30}{(n+2)(n−5)(n+3)}\)
我们用来减去具有不同分母的有理表达式的过程与加法的过程相同。 在减去分子时,我们只需要非常小心符号即可。
减去:\(\dfrac{8y}{y^2−16}−\dfrac{4}{y−4}\)。
解决方案
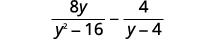 |
|
| 这些表达式有共同点吗? | 不。 |
| 使用 LCD 重写每个表达式。 | |
| \(\begin{array} {ll} \text{Find the LCD.} &\begin{array} {l} y^2−16=(y−4)(y+4) \\ \quad \underline{y−4=y−4} \\ LCD=(y−4)(y+4) \end{array} \end{array} \) | |
| 使用 LCD 将每个有理表达式重写为 等效的有理表达式。 |
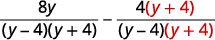 |
| 简化分子。 | 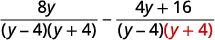 |
| 减去有理表达式。 | 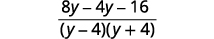 |
| 简化分子。 | 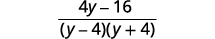 |
| 将分子分解以寻找常见因子。 | 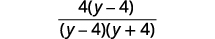 |
| 移除常见因素 | 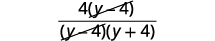 |
| 简化。 | 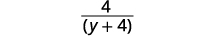 |
减去:\(\dfrac{2x}{x^2−4}−\dfrac{1}{x+2}\)。
- 回答
-
\(\dfrac{1}{x−2}\)
减去:\(\dfrac{3}{z+3}−\dfrac{6z}{z^2−9}\)。
- 回答
-
\(\dfrac{−3}{z−3}\)
下一个例子中有很多负面信号。 要格外小心。
减去:\(\dfrac{−3n−9}{n^2+n−6}−\dfrac{n+3}{2−n}\)。
解决方案
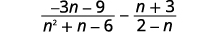 |
|
| 将分母考虑在内。 | 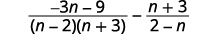 |
| 由于\(n−2\)和\(2−n\)是对立的,我们将第二个有理表达式 乘以\(\dfrac{−1}{−1}\)。 |
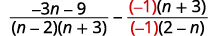 |
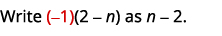 |
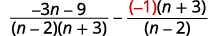 |
| 简化。 记住,\(a−(−b)=a+b\)。 | 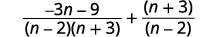 |
| 有理表达式有 共同点吗? 不。 |
|
| \(\begin{array} {ll} \text{Find the LCD.} &\begin{array} {l} n^2+n−6=(n−2)(n+3) \\ \quad\underline{n−2=(n−2)} \\ LCD=\quad (n−2)(n+3) \end{array} \end{array} \) | |
| 使用 LCD 将每个有理表达式重写为 等效的有理表达式。 |
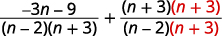 |
| 简化分子。 | 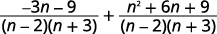 |
| 添加有理表达式。 | 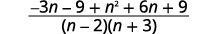 |
| 简化分子。 | 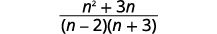 |
| 将分子分解以寻找常见因子。 | 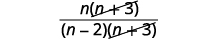 |
| 简化。 | 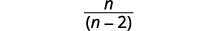 |
减去:\(\dfrac{3x−1}{x^2−5x−6}−\dfrac{2}{6−x}\)。
- 回答
-
\(\dfrac{5x+1}{(x−6)(x+1)}\)
减去:\(\dfrac{−2y−2}{y^2+2y−8}−\dfrac{y−1}{2−y}\)。
- 回答
-
\(\dfrac{y+3}{y+4}\)
当必须将两个分数乘以二项式才能得到公分母时,事情可能会变得非常混乱。
减去:\(\dfrac{4}{a^2+6a+5}−\dfrac{3}{a^2+7a+10}\)。
解决方案
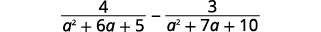 |
|
| 将分母考虑在内。 | 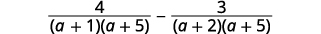 |
| 有理表达式有 共同点吗? 不。 |
|
|
\(\begin{array} {ll} \text{Find the LCD.} &\begin{array} {l} a^2+6a+5=(a+1)(a+5) \\ \underline{a^2+7a+10=(a+5)(a+2)} \\ LCD=(a+1)(a+5)(a+2) \end{array} \end{array} \) |
|
| 使用 LCD 将每个有理表达式重写为 等效的有理表达式。 |
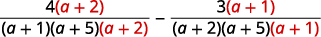 |
| 简化分子。 | 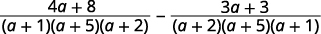 |
| 减去有理表达式。 | 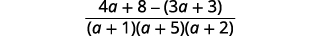 |
| 简化分子。 | 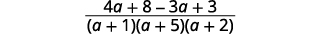 |
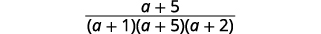 |
|
| 寻找常见因素。 | 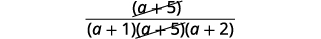 |
| 简化。 | 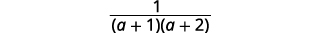 |
减去:\(\dfrac{3}{b^2−4b−5}−\dfrac{2}{b^2−6b+5}\)。
- 回答
-
\(\dfrac{1}{(b+1)(b−1)}\)
减去:\(\dfrac{4}{x^2−4}−\dfrac{3}{x^2−x−2}\)。
- 回答
-
\(\dfrac{1}{(x+2)(x+1)}\)
当我们有两个以上的有理表达式时,我们会按照与以前相同的步骤找到液晶屏。 在下一个示例中,我们将首先分解所有三个分母以找到它们的液晶显示屏。
简化:\(\dfrac{2u}{u−1}+\dfrac{1}{u}−\dfrac{2u−1}{u^2−u}\)。
解决方案
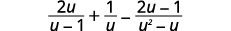 |
|
| 这些表达式有共同点吗? 不。 使用 LCD 重写每个表达式。 |
|
| \(\begin{array} {ll} \text{Find the LCD.} &\begin{array} {l} u−1=(u−1) \\ u=u \\ \underline{u^2−u=u(u−1)} \\ LCD=u(u−1) \end{array} \end{array}\) | |
| 使用 LCD 将每个有理表达式重写为 等效的有理表达式。 |
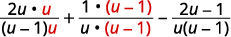 |
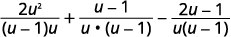 |
|
| 写成一个理性表达。 | 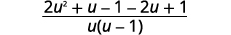 |
| 简化。 | 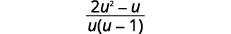 |
| 将分子分解并移除 常见因子。 |
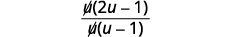 |
| 简化。 | 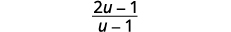 |
简化:\(\dfrac{v}{v+1}+\dfrac{3}{v−1}−\dfrac{6}{v^2−1}\)。
- 回答
-
\(\dfrac{v+3}{v+1}\)
简化:\(\dfrac{3w}{w+2}+\dfrac{2}{w+7}−\dfrac{17w+4}{w^2+9w+14}\)。
- 回答
-
\(\dfrac{3w}{w+7}\)
加减有理函数
要加上或减去有理函数,我们使用与添加或减去多项式函数相同的技术。
找出\(R(x)=f(x)−g(x)\)位置\(f(x)=\dfrac{x+5}{x−2}\)和\(g(x)=\dfrac{5x+18}{x^2−4}\).
- Elution
-

在函数中替换\(f(x)\),\(g(x)\)。 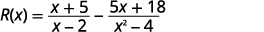
将分母考虑在内。 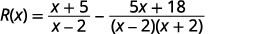
这些表达式有共同点吗? 不。
使用 LCD 重写每个表达式。\(\begin{array} {ll} \text{Find the LCD.} &\begin{array} {l} x−2=(x−2) \\ \underline{x^2−4=(x−2)(x+2)} \\ \hspace{4mm} LCD=(x−2)(x+2)\end{array} \end{array}\) 使用 LCD 将每个有理表达式重写为
等效的有理表达式。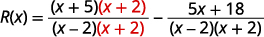
写成一个理性表达。 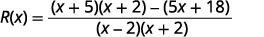
简化。 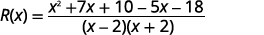
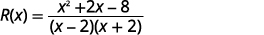
将分子分解并移除
常见因子。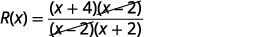
简化。 
找出\(R(x)=f(x)−g(x)\)位置\(f(x)=\dfrac{x+1}{x+3}\)和\(g(x)=\dfrac{x+17}{x^2−x−12}\).
- 回答
-
\(\dfrac{x−7}{x−4}\)
找出\(R(x)=f(x)+g(x)\)位置\(f(x)=\dfrac{x−4}{x+3}\)和\(g(x)=\dfrac{4x+6}{x^2−9}\).
- 回答
-
\(\dfrac{x^2−3x+18}{(x+3)(x−3)}\)
访问此在线资源,获取有关加减有理表达式的更多指导和练习。
- 加减有理表达式-与分母不同
关键概念
- 有理表达式加减
如果\(p\)\(q\)、和\(r\)是多项式在哪里\(r\neq 0\),那么
\[\dfrac{p}{r}+\dfrac{q}{r}=\dfrac{p+q}{r} \quad \text{and} \quad \dfrac{p}{r}−\dfrac{q}{r}=\dfrac{p−q}{r}\nonumber\] - 如何找到有理表达式的最小公分母。
- 对每个表达式进行完全分解。
- 列出每个表达式的因子。 尽可能垂直匹配因子。
- 把柱子放下。
- 将液晶屏写成因素的乘积。
- 如何添加或减去有理表达式。
- 确定表达式是否有公分母。
- 是-转到步骤 2。
- 否 — 使用 LCD 重写每个有理表达式。
- 找到液晶屏。
- 使用 LCD 将每个有理表达式重写为等效的有理表达式。
- 加上或减去有理表达式。
- 尽可能简化。
- 确定表达式是否有公分母。


