6.5: 分解多项式表达式的通用策略
- Page ID
- 203912
在本节结束时,您将能够:
- 识别并使用适当的方法将多项式完全分解
识别并使用适当的方法完全分解多项式
现在,您已经熟悉了本课程中需要的所有保理方法。 下表总结了我们介绍的所有分解方法,并概述了在分解多项式时应使用的策略。

- 有最大的共同因素吗?
把它排除在外。 - 多项式是二项式、三项式还是超过三个项?
如果是二项式:- 这是总和吗?
正方形? 平方和不分解。
多维数据集? 使用立方体总和模式。 - 有区别吗?
正方形? 因子是共轭物的乘积。
多维数据集? 使用立方体差异图案。
- 是这样的吗\(x^2+bx+c\)? 撤消 FOIL。
- 是这样的吗\(ax^2+bx+c\)?
如果 a 和 c 是正方形,请检查它是否符合三项式方形图案。
使用反复试验或 “\(ac\)” 方法。
- 使用分组方法。
- 这是总和吗?
- 查看。
完全考虑了吗?
这些因子会乘回原来的多项式吗?
请记住,如果除单项式以外,多项式的因子是素数,则该多项式是完全分解的!
完全考虑因素:\(7x^3−21x^2−70x\).
解决方案
\(\begin{array} {ll} {7x^3−21x^2−70x} & \\ \text{Is there a GCF? Yes, }7x. & \\ \text{Factor out the GCF.} &7x(x^2−3x−10) \\ \text{In the parentheses, is it a binomial, trinomial,} & \\ \text{or are there more terms?} & \\ \text{Trinomial with leading coefficient 1.} & \\ \text{“Undo” FOIL.} &7x(x\hspace{8mm})(x\hspace{8mm}) \\ &7x(x+2)(x−5) \\ \text{Is the expression factored completely? Yes.} & \\ \text{Neither binomial can be factored.} & \\ \text{Check your answer.} & \\ \text{Multiply.} & \\ & \\ & \\ \hspace{15mm}7x(x+2)(x−5) & \\ \hspace{10mm}7x(x^2−5x+2x−10) & \\ \hspace{15mm}7x(x^2−3x−10) & \\ \hspace{13mm}7x^3−21x^2−70x\checkmark & \end{array} \)
完全考虑因素:\(8y^3+16y^2−24y\).
- 回答
-
\(8y(y−1)(y+3)\)
完全考虑因素:\(5y^3−15y^2−270y\).
- 回答
-
\(5y(y−9)(y+6)\)
当你被要求分解二项式时要小心,因为有几个选项!
完全考虑以下因素:\(24y^2−150\)
解决方案
\(\begin{array} {ll} &24y^2−150 \\ \text{Is there a GCF? Yes, }6. & \\ \text{Factor out the GCF.} &6(4y^2−25) \\ \text{In the parentheses, is it a binomial, trinomial} & \\ \text{or are there more than three terms? Binomial.} & \\ \text{Is it a sum? No.} & \\ \text{Is it a difference? Of squares or cubes? Yes, squares.} &6((2y)^2−(5)^2) \\ \text{Write as a product of conjugates.} &6(2y−5)(2y+5) \\ & \\ & \\ \hspace{5mm}\text{Is the expression factored completely?} & \\ \hspace{5mm}\text{Neither binomial can be factored.} & \\ \text{Check:} & \\ & \\ & \\ \hspace{5mm}\text{Multiply.} & \\ & \\ \hspace{15mm}6(2y−5)(2y+5) & \\ & \\ \hspace{18mm}6(4y^2−25) & \\ \hspace{18mm}24y^2−150\checkmark \end{array}\)
完全考虑因素:\(16x^3−36x\).
- 回答
-
\(4x(2x−3)(2x+3)\)
完全考虑因素:\(27y^2−48\).
- 回答
-
\(3(3y−4)(3y+4)\)
下一个示例可以使用多种方法进行分解。 识别三项式正方形模式将使您的工作更轻松。
完全考虑因素:\(4a^2−12ab+9b^2\).
解决方案
\(\begin{array} {ll} &4a^2−12ab+9b^2 \\ \text{Is there a GCF? No.} & \\ \text{Is it a binomial, trinomial, or are there more terms?} & \\ \text{Trinomial with }a\neq 1.\text{ But the first term is a perfect square.} \\ \text{Is the last term a perfect square? Yes.} &(2a)^2−12ab+(3b)^2 \\ \text{Does it fit the pattern, }a^2−2ab+b^2?\text{ Yes.} &(2a)^2 −12ab+ (3b)^2 \\ &\hspace{7mm} {\,}^{\searrow}{\,}_{−2(2a)(3b)}{\,}^{\swarrow}\\ \text{Write it as a square.} &(2a−3b)^2 \\ & \\ & \\ \quad\text{Is the expression factored completely? Yes.} & \\ \quad\text{The binomial cannot be factored.} & \\ \text{Check your answer.} \\ & \\ & \\ \quad\text{Multiply.} & \\ \hspace{30mm}(2a−3b)^2 \\ \hspace{20mm} (2a)^2−2·2a·3b+(3b)^2 \\ \hspace{24mm}4a^2−12ab+9b^2\checkmark & \end{array} \)
完全考虑因素:\(4x^2+20xy+25y^2\).
- 回答
-
\((2x+5y)^2\)
完全考虑因素:\(9x^2−24xy+16y^2\).
- 回答
-
\((3x−4y)^2\)
请记住,平方和不分解,但立方之和是分数!
完全考虑因素\(12x^3y^2+75xy^2\)。
解决方案
\(\begin{array} {ll} &12x^3y^2+75xy^2 \\ \text{Is there a GCF? Yes, }3xy^2. & \\ \text{Factor out the GCF.} &3xy^2(4x^2+25) \\ \text{In the parentheses, is it a binomial, trinomial, or are} & \\ \text{there more than three terms? Binomial.} & \\ & \\ \text{Is it a sum? Of squares? Yes.} &\text{Sums of squares are prime.} \\ & \\ & \\ \quad\text{Is the expression factored completely? Yes.} & \\ \text{Check:} & \\ & \\ & \\ \quad\text{Multiply.} & \\ \hspace{15mm}3xy^2(4x^2+25) & \\ \hspace{14mm}12x^3y^2+75xy^2\checkmark \end{array} \)
完全考虑因素:\(50x^3y+72xy\).
- 回答
-
\(2xy(25x^2+36)\)
完全考虑因素:\(27xy^3+48xy\).
- 回答
-
\(3xy(9y^2+16)\)
使用立方体之和或差值模式时,请注意符号。
完全考虑因素:\(24x^3+81y^3\).
解决方案
| 有全球气候基金吗? 是的,3。 | 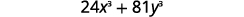 |
| 把它排除在外。 | 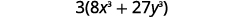 |
| 在括号中,它是二项式、三项式还是有三个以上的项? 二项式。 |
|
| 是总和还是差异? 总和。 | |
| 正方形还是立方体? 立方体总和。 | 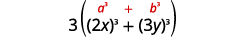 |
| 使用立方体总和模式进行编写。 | 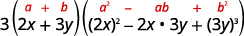 |
| 这个表达式是完全考虑的吗? 是的。 | 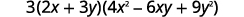 |
| 乘法检查。 |
完全考虑因素:\(250m^3+432n^3\).
- 回答
-
\(2(5m+6n)(25m^2−30mn+36n^2)\)
完全考虑因素:\(2p^3+54q^3\).
- 回答
-
\(2(p+3q)(p^2−3pq+9q^2)\)
完全考虑因素:\(3x^5y−48xy\).
解决方案
\(\begin{array} {ll} &3x^5y−48xy \\ \text{Is there a GCF? Factor out }3xy &3xy(x^4−16) \\ \begin{array} {l} \text{Is the binomial a sum or difference? Of squares or cubes?} \\ \text{Write it as a difference of squares.} \end{array} &3xy\left((x^2)^2−(4)2\right) \\ \text{Factor it as a product of conjugates} &3xy(x^2−4)(x^2+4) \\ \text{The first binomial is again a difference of squares.} &3xy\left((x)^2−(2)^2\right)(x^2+4) \\ \text{Factor it as a product of conjugates.} &3xy(x−2)(x+2)(x^2+4) \\ \text{Is the expression factored completely? Yes.} & \\ \text{Check your answer.} & \\ \text{Multiply.} & \\ 3xy(x−2)(x+2)(x^2+4) & \\ 3xy(x^2−4)(x^2+4) & \\ 3xy(x^4−16) & \\ 3x^5y−48xy\checkmark & \end{array}\)
完全考虑因素:\(4a^5b−64ab\).
- 回答
-
\(4ab(a^2+4)(a−2)(a+2)\)
完全考虑因素:\(7xy^5−7xy\).
- 回答
-
\(7xy(y^2+1)(y−1)(y+1)\)
完全考虑因素:\(4x^2+8bx−4ax−8ab\).
解决方案
\(\begin{array} {ll} &4x^2+8bx−4ax−8ab \\ \text{Is there a GCF? Factor out the GCF, }4. &4(x^2+2bx−ax−2ab) \\ \text{There are four terms. Use grouping.} &4[x(x+2b)−a(x+2b)]4(x+2b)(x−a) \\ \text{Is the expression factored completely? Yes.} & \\ \text{Check your answer.} & \\ \text{Multiply.} & \\ \hspace{25mm}4(x+2b)(x−a) & \\ \hspace{20mm} 4(x^2−ax+2bx−2ab) & \\ \hspace{20mm}4x^2+8bx−4ax−8ab\checkmark \end{array}\)
完全考虑因素:\(6x^2−12xc+6bx−12bc\).
- 回答
-
\(6(x+b)(x−2c)\)
完全考虑因素:\(16x^2+24xy−4x−6y\).
- 回答
-
\(2(4x−1)(2x+3y)\)
在第一步中取出完整的 GCF 总是会让你的工作更轻松。
完全考虑因素:\(40x^2y+44xy−24y\).
解决方案
\(\begin{array} {ll} &40x^2y+44xy−24y \\ \text{Is there a GCF? Factor out the GCF, }4y. &4y(10x^2+11x−6) \\ \text{Factor the trinomial with }a\neq 1. &4y(10x^2+11x−6) \\ &4y(5x−2)(2x+3) \\ \text{Is the expression factored completely? Yes.} & \\ \text{Check your answer.} & \\ \text{Multiply.} & \\ \hspace{25mm}4y(5x−2)(2x+3) & \\ \hspace{24mm}4y(10x^2+11x−6) & \\ \hspace{22mm}40x^2y+44xy−24y\checkmark \end{array}\)
完全考虑因素:\(4p^2q−16pq+12q\).
- 回答
-
\(4q(p−3)(p−1)\)
完全考虑因素:\(6pq^2−9pq−6p\).
- 回答
-
\(3p(2q+1)(q−2)\)
当我们对具有四个项的多项式进行分解时,通常将其分成两组,每组两个项。 请记住,我们也可以将其分为三项式,然后再分为一个项。
完全考虑因素:\(9x^2−12xy+4y^2−49\).
解决方案
\(\begin{array} {ll} &9x^2−12xy+4y^2−49 \\ \text{Is there a GCF? No.} & \\ \begin{array} {l} \text{With more than 3 terms, use grouping. Last 2 terms} \\ \text{have no GCF. Try grouping first 3 terms.} \end{array} &9x^2−12xy+4y^2−49 \\ \begin{array} {l} \text{Factor the trinomial with }a\neq 1. \text{ But the first term is a} \\ \text{perfect square.} \end{array} & \\ \text{Is the last term of the trinomial a perfect square? Yes.} &(3x)^2−12xy+(2y)^2−49 \\ \text{Does the trinomial fit the pattern, }a^2−2ab+b^2? \text{ Yes.} &(3x)^2 −12xy+ (2y)^2−49 \\ &\hspace{7mm} {\,}^{\searrow}{\,}_{−2(3x)(2y))}{\,}^{\swarrow} \\ \text{Write the trinomial as a square.} &(3x−2y)^2−49 \\ \begin{array} {ll} \text{Is this binomial a sum or difference? Of squares or} \\ \text{cubes? Write it as a difference of squares.} \end{array} &(3x−2y)^2−72 \\ \text{Write it as a product of conjugates.} &((3x−2y)−7)((3x−2y)+7) \\ &(3x−2y−7)(3x−2y+7) \\ \text{Is the expression factored completely? Yes.} & \\ \text{Check your answer.} & \\ \text{Multiply.} & \\ \hspace{23mm}(3x−2y−7)(3x−2y+7) & \\ \hspace{10mm}9x^2−6xy−21x−6xy+4y^2+14y+21x−14y−49 \qquad & \\ \hspace{25mm}9x^2−12xy+4y^2−49\checkmark & \end{array}\)
完全考虑因素:\(4x^2−12xy+9y^2−25\).
- 回答
-
\((2x−3y−5)(2x−3y+5)\)
完全考虑因素:\(16x^2−24xy+9y^2−64\).
- 回答
-
\((4x−3y−8)(4x−3y+8)\)
关键概念

- 如何使用通用策略对多项式进行分解。
- 有最大的共同因素吗?
把它排除在外。 - 多项式是二项式、三项式还是超过三个项?
如果是二项式:
是总和吗?
正方形? 平方和不分解。
多维数据集? 使用立方体总和模式。
有区别吗?
正方形? 因子是共轭物的乘积。
多维数据集? 使用立方体差异图案。
如果是三项式:
是这样的\(x^2+bx+c\)吗? 撤消 FOIL。
是这样的吗\(ax^2+bx+c\)?
如果 a 和 c 是正方形,请检查它是否符合三项式方形图案。
使用反复试验或 “\(ac\)” 方法。
如果它有三个以上的术语:
使用分组方法。 - 查看。
完全考虑了吗?
这些因子会乘回原来的多项式吗?
- 有最大的共同因素吗?


