6.4: Factor 特殊产品
- Page ID
- 203941
在本节结束时,您将能够:
- 因子完美方形三项式
- 正方形的因子差
- 因子总和和和与立方差
在开始之前,请参加这个准备测验。
- 简化:\((3x^2)^3\)。
- 乘以:\((m+4)^2\)。
- 乘以:\((x−3)(x+3)\)。
我们已经看到,一些二项式和三项式是由特殊乘积产生的,即二项式的平方和乘法共轭物。 如果你学会识别这类多项式,你可以使用特殊乘积模式更快地分解它们。
Factor Perfect Square 三项式
有些三项式是完美的正方形。 它们是通过将二项式乘以本身得出的。 在上一章中,我们使用二项式方块模式对二项式进行了平方。
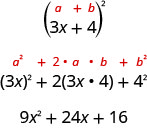
三项式\(9x^2+24x+16\)被称为完美正方形三项式。 它是二项式的平方\(3x+4\)。
在本章中,你将从一个完美的正方三项式开始,然后将其分解为其素数。 你可以使用上一节中描述的方法来分解这个三项式,因为它的形式是这样的\(ax^2+bx+c\)。 但是,如果你认识到第一个和最后一个项是正方形,而三项式符合完美的方形三项式模式,那么你可以为自己节省很多工作。 这是图案——与二项式方块图案相反。
如果\(a\)和\(b\)是实数
\[a^2+2ab+b^2=(a+b)^2\nonumber\]
\[a^2−2ab+b^2=(a−b)^2\nonumber\]
要使用这种模式,你必须认识到给定的三项式适合它。 首先检查前导系数是否为完美正方形\(a^2\)。 接下来检查最后一个术语是否是完美的正方形,\(b^2\)。 然后检查中间术语——是产品\(2ab\)吗,? 如果一切正常,你可以很容易地写出因子。
因子:\(9x^2+12x+4\)。
- 回答
-



因子:\(4x^2+12x+9\)。
- 回答
-
\((2x+3)^2\)
因子:\(9y^2+24y+16\)。
- 回答
-
\((3y+4)^2\)
中间术语的符号决定了我们将使用哪种模式。 当中间术语为负数时,我们使用模式\(a^2−2ab+b^2\),其因素是\((a−b)^2\)。
这里总结了这些步骤。
\(\begin{array} {lllll} \textbf{Step 1.} &\text{Does the trinomial fit the pattern?} &\quad &\hspace{7mm} a^2+2ab+b^2 &\hspace{7mm} a^2−2ab+b^2 \\ &\text{Are the first and last terms perfect squares?} &\quad & &\\ &\text{Write them as squares.} &\quad &\hspace{5mm}(a)^2\hspace{16mm} (b)^2 &\hspace{6mm}(a)^2\hspace{16mm} (b)^2 \\ &\text{Check the middle term. Is it }2ab? &\quad &\hspace{12mm} {\,}^{\searrow}{\,}_{2·a·b}{\,}^{\swarrow} &\hspace{12mm} {\,}^{\searrow}{\,}_{2·a·b}{\,}^{\swarrow} \\ \textbf{Step 2.} &\text{Write the square of the binomial.} &\quad &\hspace{13mm} (a+b)^2 &\hspace{13mm} (a−b)^2 \\ \textbf{Step 3.} &\text{Check by multiplying.} & & & \end{array}\)
我们现在要研究一个中间术语为负值的地方。
因子:\(81y^2−72y+16\)。
- 回答
-
第一个和最后一个项是平方。 看看中间术语是否符合完美方形三项式的模式。 中间项是负数,所以二项式平方是负数\((a−b)^2\)。
\(81 y^{2}-72 y+16\) 第一个和最后一个项是完美的正方形吗? 
查看中间术语。 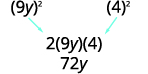
它匹配\((a−b)^2\)吗? 是的。 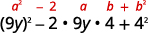
写成二项式的平方。 \((9 y-4)^{2}\) 乘以检查:
\[(9y−4)^2\nonumber\]\[(9y)^2−2·9y·4+4^2\nonumber\]\[81y^2−72y+16\checkmark\nonumber\]
因子:\(64y^2−80y+25\)。
- 回答
-
\((8y−5)^2\)
因子:\(16z^2−72z+81\)。
- 回答
-
\((4z−9)^2\)
下一个例子将是具有两个变量的完美平方三项式。
因子:\(36x^2+84xy+49y^2\)。
- 回答
-
\(36 x^{2}+84 x y+49 y^{2}\) 测试每个术语以验证模式。 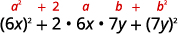
因子。 \((6 x+7 y)^{2}\) 乘法检查。
\[(6x+7y)^2\nonumber\]\[(6x)^2+2·6x·7y+(7y)^2\nonumber\]\[36x^2+84xy+49y^2\checkmark\nonumber\]
因子:\(49x^2+84xy+36y^2\)。
- 回答
-
\((7x+6y)^2\)
因子:\(64m^2+112mn+49n^2\)。
- 回答
-
\((8m+7n)^2\)
请记住,保理的第一步是寻找最大的共同因素。 完美方三项式可能在所有三个项中都有 GCF,应该先将其分解出来。 而且,有时候,一旦考虑了 GCF,你就会认出一个完美的方形三项式。
因子:\(100x^2y−80xy+16y\)。
- 回答
-
\(100 x^{2} y-80 x y+16 y\) 有全球气候基金吗? 是的\(4y\),所以把它排除在外。 \(4 y\left(25 x^{2}-20 x+4\right)\) 这是一个完美的方形三项式吗? 验证图案。 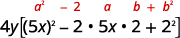
因子。 \(4 y(5 x-2)^{2}\) 记住:在最终产品中保留因子 4 y。 查看:
\[4y(5x−2)^2\nonumber\]\[4y[(5x)2−2·5x·2+22]\nonumber\]\[4y(25x2−20x+4)\nonumber\]100x2y−80xy+16y\ 复选标记\]
因子:\(8x^2y−24xy+18y\)。
- 回答
-
\(2y(2x−3)^2\)
因子:\(27p^2q+90pq+75q\)。
- 回答
-
\(3q(3p+5)^2\)
正方形的因子差
你在上一章中看到的另一个特殊产品是共轭物乘积图案。 你用它来乘以两个作为共轭物的二项式。 下面是一个例子:
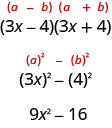
平方因子与共轭物乘积的差。
如果\(a\)和\(b\)是实数,
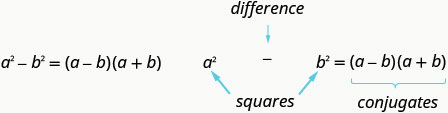
请记住,“差异” 是指减法。 因此,要使用这种模式,你必须确保你有一个二项式,其中要减去两个正方形。
因子:\(64y^2−1\)。
- 回答
-




因子:\(121m^2−1\)。
- 回答
-
\((11m−1)(11m+1)\)
因子:\(81y^2−1\)。
- 回答
-
\((9y−1)(9y+1)\)
\(\begin{array} {llll} \textbf{Step 1.} &\text{Does the binomial fit the pattern?} &\qquad &\hspace{5mm} a^2−b^2 \\ &\text{Is this a difference?} &\qquad &\hspace{2mm} \text{____−____} \\ &\text{Are the first and last terms perfect squares?} & & \\ \textbf{Step 2.} &\text{Write them as squares.} &\qquad &\hspace{3mm} (a)^2−(b)^2 \\ \textbf{Step 3.} &\text{Write the product of conjugates.} &\qquad &(a−b)(a+b) \\ \textbf{Step 4.} &\text{Check by multiplying.} & & \end{array}\)
重要的是要记住,平方和不会分解为二项式的乘积。 没有二项式因子可以相乘得出平方和。 移除任何 GCF 后,表达式\(a^2+b^2\)为 prime!
下一个示例用两个术语显示变量。
因子:\(144x^2−49y^2\)。
- 回答
-
\(\begin{array} {lll} &\quad &144x^2−49y^2 \\ \text{Is this a difference of squares? Yes.} &\quad &(12x)^2−(7y)^2 \\ \text{Factor as the product of conjugates.} &\quad &(12x−7y)(12x+7y) \\ \text{Check by multiplying.} &\quad &(12x−7y)(12x+7y) \\ \text{Check by multiplying.} &\quad & \\ &\quad & \\ &\quad & \\ \hspace{14mm} (12x−7y)(12x+7y) &\quad & \\ \hspace{21mm} 144x^2−49y^2\checkmark &\quad & \end{array}\)
因子:\(196m^2−25n^2\)。
- 回答
-
\((14m−5n)(14m+5n)\)
因子:\(121p^2−9q^2\)。
- 回答
-
\((11p−3q)(11p+3q)\)
与往常一样,每当你有要因子的表达式时,你都应该先寻找一个共同因子。 有时候,一个共同因子可能 “掩盖” 平方差,在你将 GCF 分解出来之前,你无法识别出完美的正方形。
另外,为了在下一个示例中完全分解二项式,我们将对平方差进行两次分解!
因子:\(48x^4y^2−243y^2\)。
- 回答
-
\(\begin{array} {ll} &48x^4y^2−243y^2 \\ \text{Is there a GCF? Yes, }3y^2\text{—factor it out!} &3y^2(16x^4−81) \\ \text{Is the binomial a difference of squares? Yes.} &3y^2\left((4x^2)^2−(9)^2\right) \\ \text{Factor as a product of conjugates.} &3y^2(4x^2−9)(4x^2+9) \\ \text{Notice the first binomial is also a difference of squares!} &3y^2((2x)^2−(3)^2)(4x^2+9) \\ \text{Factor it as the product of conjugates.} &3y^2(2x−3)(2x+3)(4x^2+9) \end{array}\)
最后一个因子,即平方和,不能分解。
\(\begin{array} {l} \text{Check by multiplying:} \\ \hspace{10mm} 3y^2(2x−3)(2x+3)(4x^2+9) \\ \\ \\ \hspace{15mm} 3y^2(4x^2−9)(4x^2+9) \\ \hspace{20mm} 3y^2(16x^4−81) \\ \hspace{19mm} 48x^4y^2−243y^2\checkmark\end{array}\)
因子:\(2x^4y^2−32y^2\)。
- 回答
-
\(2y^2(x−2)(x+2)(x^2+4)\)
因子:\(7a^4c^2−7b^4c^2\)。
- 回答
-
\(7c^2(a−b)(a+b)(a^2+b^2)\)
下一个示例有一个包含 4 个项的多项式。 到目前为止,当这种情况发生时,我们将术语一分为二,然后从那里开始分解。 在这里,我们将注意到前三个项构成了一个完美的正方三项式。
因子:\(x^2−6x+9−y^2\)。
- 回答
-
请注意,前三个项构成了一个完美的正方三项式。
\(x^{2}-6 x+9-y^{2}\) 通过对前三个项进行分组来进行分数。 \(\underbrace{x^{2}-6 x+9} - y^{2}\) 使用完美的方形三项式图案。 \((x-3)^{2}-y^{2}\) 这是正方差吗? 是的。 是的——把它们写成正方形。 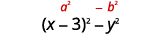
因子是共轭物的乘积。 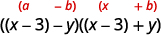
\((x-3-y)(x-3+y)\) 你可能想将解决方案重写为\((x−y−3)(x+y−3)\)。
因子:\(x^2−10x+25−y^2\)。
- 回答
-
\((x−5−y)(x−5+y)\)
因子:\(x^2+6x+9−4y^2\)。
- 回答
-
\((x+3−2y)(x+3+2y)\)
多维数据集的因子和和和差
还有另一种特殊的分解模式,我们在乘以多项式时没有使用这种模式。 这是立方体总和和和差的模式。 我们将先写出这些公式,然后通过乘法检查它们。
\[a^3+b^3=(a+b)(a^2−ab+b^2\nonumber\]
\[a^3−b^3=(a−b)(a^2+ab+b^2)\nonumber\]
我们将检查第一个图案,然后将第二个模式留给你。
| \(\color{red}(a+b) \color{black} \left(a^{2}-a b+b^{2}\right)\) | |
| 分发。 | \(\color{red}a \color{black}\left(a^{2}-a b+b^{2}\right)+ \color{red}b \color{black}\left(a^{2}-a b+b^{2}\right)\) |
| 乘以。 | \(a^{3}-a^{2} b+a b^{2}+a^{2} b-a b^{2}+b^{3}\) |
| 将相似的术语组合在一起。 | \(a^{3}+b^{3}\) |
\[a^3+b^3=(a+b)(a^2−ab+b^2\nonumber\]\[a^3−b^3=(a−b)(a^2+ab+b^2)\nonumber\]
这两种模式看起来很相似,不是吗? 但是请注意这些因素中的迹象。 二项式因子的符号与原始二项式中的符号相匹配。 而三项式因子的中间项的符号与原始二项式中的符号相反。 如果你认出标志的图案,它可能会帮助你记住这些图案。

无法考虑立方体总和差值模式中的三项式因子。
如果你学会识别 1 到 10 的整数的立方体,就像你学会识别正方形一样,这会非常有帮助。 我们在表中列出了从 1 到 10 的整数的立方体。
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| \(n^3\) | 1 | 8 | 27 | 64 | 125 | 216 | 343 | 512 | 729 | 1000 |
因子:\(x^3+64\)。
- 回答
-





因子:\(x^3+27\)。
- 回答
-
\((x+3)(x^2−3x+9)\)
因子:\(y^3+8\)。
- 回答
-
\((y+2)(y^2−2y+4)\)
- 二项式是否符合立方体模式的总和或差异?
是总和还是差异?
第一个和最后一个学期是完美的立方体吗? - 把它们写成立方体。
- 使用立方体的总和或差值模式。
- 在圆括号内简化。
- 通过乘以因子进行检查。
因子:\(27u^3−125v^3\)。
- 回答
-
\(27 u^{3}-125 v^{3}\) 这个二项式是不同的。 第一个和最后一个
术语是完美的立方体。将术语写成立方体。 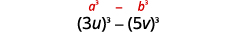
使用立方体差异图案。 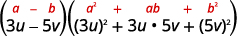
简化。 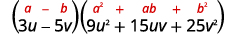
乘法检查。 我们会把支票留给你。
因子:\(8x^3−27y^3\)。
- 回答
-
\((2x−3y)(4x^2+6xy+9y^2)\)
因子:\(1000m^3−125n^3\)。
- 回答
-
\((10m−5n)(100m^2+50mn+25n^2)\)
在下一个例子中,我们首先考虑了 GCF。 然后我们就可以识别出立方体的总和了。
因子:\(6x^3y+48y^4\)。
- 回答
-
\(6 x^{3} y+48 y^{4}\) 将共同因素考虑在内。 \(6 y\left(x^{3}+8 y^{3}\right)\) 这个二项式是一个总和第一个和最后一个
项是完美的立方体。将术语写成立方体。 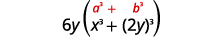
使用立方体总和模式。 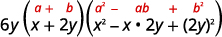
简化。 
查看:
要检查一下,你可能会发现先将立方体因子的总和相乘,然后将该乘积乘以 6y.6y 会更容易。 我们将把乘法留给你。
因子:\(500p^3+4q^3\)。
- 回答
-
\(4(5p+q)(25p^2−5pq+q^2)\)
因子:\(432c^3+686d^3\)。
- 回答
-
\(2(6c+7d)(36c^2−42cd+49d^2)\)
下一个示例中的第一个项是二项式立方体。
因子:\((x+5)^3−64x^3\)。
- 回答
-
\((x+5)^{3}-64 x^{3}\) 这个二项式是不同的。 第一个和
最后一个术语是完美的立方体。将术语写成立方体。 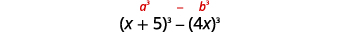
使用立方体差异图案。 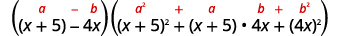
简化。 \((x+5-4 x)\left(x^{2}+10 x+25+4 x^{2}+20 x+16 x^{2}\right)\) \((-3 x+5)\left(21 x^{2}+30 x+25\right)\) 乘法检查。 我们会把支票留给你。
因子:\((y+1)^3−27y^3\)。
- 回答
-
\((−2y+1)(13y^2+5y+1)\)
因子:\((n+3)^3−125n^3\)。
- 回答
-
\((−4n+3)(31n^2+21n+9)\)
访问此在线资源,获取有关保理特殊产品的更多指导和实践。
关键概念
- 完美方形三项式图案:如果 a 和 b 是实数,
\[\begin{array} {l} a^2+2ab+b^2=(a+b)^2 \\ a^2−2ab+b^2=(a−b)^2\end{array} \nonumber\]
- 如何分解完美的正方三项式。
\(\begin{array} {lllll} \textbf{Step 1.} &\text{Does the trinomial fit the pattern?} &\quad &\hspace{7mm} a^2+2ab+b^2 &\hspace{7mm} a^2−2ab+b^2 \\ &\text{Are the first and last terms perfect squares?} &\quad & &\\ &\text{Write them as squares.} &\quad &\hspace{5mm}(a)^2\hspace{16mm} (b)^2 &\hspace{6mm}(a)^2\hspace{16mm} (b)^2 \\ &\text{Check the middle term. Is it }2ab? &\quad &\hspace{12mm} {\,}^{\searrow}{\,}_{2·a·b}{\,}^{\swarrow} &\hspace{12mm} {\,}^{\searrow}{\,}_{2·a·b}{\,}^{\swarrow} \\ \textbf{Step 2.} &\text{Write the square of the binomial.} &\quad &\hspace{13mm} (a+b)^2 &\hspace{13mm} (a−b)^2 \\ \textbf{Step 3.} &\text{Check by multiplying.} & & & \end{array}\) - 方差模式:如果 a、ba、b 是实数,
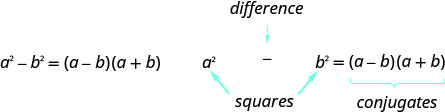
- 如何分解平方差。
\(\begin{array} {llll} \textbf{Step 1.} &\text{Does the binomial fit the pattern?} &\qquad &\hspace{5mm} a^2−b^2 \\ &\text{Is this a difference?} &\qquad &\hspace{2mm} \text{____−____} \\ &\text{Are the first and last terms perfect squares?} & & \\ \textbf{Step 2.} &\text{Write them as squares.} &\qquad &\hspace{3mm} (a)^2−(b)^2 \\ \textbf{Step 3.} &\text{Write the product of conjugates.} &\qquad &(a−b)(a+b) \\ \textbf{Step 4.} &\text{Check by multiplying.} & & \end{array}\) - 多维数据集的总和与差值模式
\(\begin{array} {l} a^3+b3=(a+b)(a^2−ab+b^2) \\ a^3−b^3=(a−b)(a^2+ab+b^2) \end{array} \) - 如何分解立方体的总和或差值。
- 二项式是否符合立方体模式的总和或差异?
是总和还是差异?
第一个和最后一个学期是完美的立方体吗? - 把它们写成立方体。
- 使用立方体的总和或差值模式。
- 在圆括号内简化
- 通过乘以因子进行检查。
- 二项式是否符合立方体模式的总和或差异?


