6.3E：练习

练习成就完美

形式的因子三项式\(x^2+bx+c\)

在以下练习中，将表格的每个三项式分解为因子\(x^2+bx+c\)。

1。 \(p^2+11p+30\)

回答

\((p+5)(p+6)\)

2。 \(w^2+10w+21\)

3。 \(n^2+19n+48\)

回答

\((n+3)(n+16)\)

4。 \(b^2+14b+48\)

5。 \(a^2+25a+100\)

回答

\((a+5)(a+20)\)

6。 \(u^2+101u+100\)

7。 \(x^2−8x+12\)

回答

\((x−2)(x−6)\)

8。 \(q^2−13q+36\)

9。 \(y^2−18y+45\)

回答

\((y−3)(y−15)\)

10。 \(m^2−13m+30\)

11。 \(x^2−8x+7\)

回答

\((x−1)(x−7)\)

12。 \(y^2−5y+6\)

13。 \(5p−6+p^2\)

回答

\((p−1)(p+6)\)

14。 \(6n−7+n^2\)

15。 \(8−6x+x^2\)

回答

\((x−4)(x−2)\)

16。 \(7x+x^2+6\)

17。 \(x^2−12−11x\)

回答

\((x−12)(x+1)\)

18。 \(−11−10x+x^2\)

在以下练习中，将表格的每个三项式分解为因子\(x^2+bxy+cy^2\)。

19。 \(x^2−2xy−80y^2\)

回答

\((x+8y)(x−10y)\)

20。 \(p^2−8pq−65q^2\)

21。 \(m^2−64mn−65n^2\)

回答

\((m+n)(m−65n)\)

22。 \(p^2−2pq−35q^2\)

23。 \(a^2+5ab−24b^2\)

回答

\((a+8b)(a−3b)\)

24。 \(r^2+3rs−28s^2\)

25。 \(x^2−3xy−14y^2\)

回答

主要

26。 \(u^2−8uv−24v^2\)

27。 \(m^2−5mn+30n^2\)

回答

主要

28。 \(c^2−7cd+18d^2\)

\(ax^2+bx+c\)使用反复试验的形式因子三项式

在以下练习中，使用反复试验来完全考虑因素。

29。 \(p^3−8p^2−20p\)

回答

\(p(p−10)(p+2)\)

30。 \(q^3−5q^2−24q\)

31。 \(3m^3−21m^2+30m\)

回答

\(3m(m−5)(m−2)\)

32。 \(11n^3−55n^2+44n\)

33。 \(5x^4+10x^3−75x^2\)

回答

\(5x^2(x−3)(x+5)\)

34。 \(6y^4+12y^3−48y^2\)

35。 \(2t^2+7t+5\)

回答

\((2t+5)(t+1)\)

36。 \(5y^2+16y+11\)

37。 \(11x^2+34x+3\)

回答

\((11x+1)(x+3)\)

38。 \(7b^2+50b+7\)

39。 \(4w^2−5w+1\)

回答

\((4w−1)(w−1)\)

40。 \(5x^2−17x+6\)

41。 \(4q^2−7q−2\)

回答

\((4q+1)(q−2)\)

42。 \(10y^2−53y−111\)

43。 \(6p^2−19pq+10q^2\)

回答

\((2p−5q)(3p−2q)\)

44。 \(21m^2−29mn+10n^2\)

45。 \(4a^2+17ab−15b^2\)

回答

\((4a−3b)(a+5b)\)

46。 \(6u^2+5uv−14v^2\)

47。 \(−16x^2−32x−16\)

回答

\(−16(x+1)(x+1)\)

48。 \(−81a^2+153a+18\)

49。 \(−30q^3−140q^2−80q\)

回答

\( - 10q(3q+2)(q+4)\)

50。 \(−5y^3−30y^2+35y\)

\(ax^2+bx+c\)使用 “ac” 方法的形式因子三项式

在以下练习中，使用 'ac' 方法进行分数。

51。 \(5n^2+21n+4\)

回答

\((5n+1)(n+4)\)

52。 \(8w^2+25w+3\)

53。 \(4k^2−16k+15\)

回答

\((2k−3)(2k−5)\)

54。 \(5s^2−9s+4\)

55。 \(6y^2+y−15\)

回答

\((3y+5)(2y−3)\)

56。 \(6p^2+p−22\)

57。 \(2n^2−27n−45\)

回答

\((2n+3)(n−15)\)

58。 \(12z^2−41z−11\)

59。 \(60y^2+290y−50\)

回答

\(10(6y−1)(y+5)\)

60。 \(6u^2−46u−16\)

61。 \(48z^3−102z^2−45z\)

回答

\(3z(8z+3)(2z−5)\)

62。 \(90n^3+42n^2−216n\)

63。 \(16s^2+40s+24\)

回答

\(8(2s+3)(s+1)\)

64。 \(24p^2+160p+96\)

65。 \(48y^2+12y−36\)

回答

\(12(4y−3)(y+1)\)

66。 \(30x^2+105x−60\)

使用替代的因子

在以下练习中，使用替换进行分解。

67。 \(x^4−x^2−12\)

回答

\((x^2+3)(x^2−4)\)

68。 \(x^4+2x^2−8\)

69。 \(x^4−3x^2−28\)

回答

\((x^2−7)(x^2+4)\)

70。 \(x^4−13x^2−30\)

71。 \((x−3)^2−5(x−3)−36\)

回答

\((x−12)(x+1)\)

72。 \((x−2)^2−3(x−2)−54\)

73。 \((3y−2)^2−(3y−2)−2\)

回答

\((3y−4)(3y−1)\)

74。 \((5y−1)^2−3(5y−1)−18\)

混合练习

在以下练习中，使用任意方法对每个表达式进行分解。

75。 \(u^2−12u+36\)

回答

\((u−6)(u−6)\)

76。 \(x^2−14x−32\)

77。 \(r^2−20rs+64s^2\)

回答

\((r−4s)(r−16s)\)

78。 \(q^2−29qr−96r^2\)

79。 \(12y^2−29y+14\)

回答

\((4y−7)(3y−2)\)

80。 \(12x^2+36y−24z\)

81。 \(6n^2+5n−4\)

回答

\((2n−1)(3n+4)\)

82。 \(3q^2+6q+2\)

83。 \(13z^2+39z−26\)

回答

\(13(z^2+3z−2)\)

84。 \(5r^2+25r+30\)

85。 \(3p^2+21p\)

回答

\(3p(p+7)\)

86。 \(7x^2−21x\)

87。 \(6r^2+30r+36\)

回答

\(6(r+2)(r+3)\)

88。 \(18m^2+15m+3\)

89。 \(24n^2+20n+4\)

回答

\(4(2n+1)(3n+1)\)

90。 \(4a^2+5a+2\)

91。 \(x^4−4x^2−12\)

回答

\((x^2+2)(x^2−6)\)

92。 \(x^4−7x^2−8\)

93。 \((x+3)^2−9(x+3)−36\)

回答

\((x−9)(x+6)\)

94。 \((x+2)^2−25(x+2)−54\)

写作练习

95。 \(x^2+bx+c\)形状的许多三项式是两个二项式的乘积\((x+m)(x+n)\)。 解释如何找到\(m\)和的值\(n\)。

回答

答案会有所不同。

96。 汤米考虑\(x^2−x−20\)为\((x+5)(x−4)\). 萨拉将其视为\((x+4)(x−5)\). 埃内斯托将其考虑为\((x−5)(x−4)\)。 谁是正确的？ 解释为什么另外两个错了。

97。 按顺序列出使用 “\(ac\)” 方法分解表单的三项式时所采取的所有步骤\(ax^2+bx+c\)。

回答

答案会有所不同。

98。 “\(ac\)” 方法与 “撤消 FOIL” 方法有何相似之处？ 有什么不同？

自检

a. 完成练习后，使用此清单评估您对本节目标的掌握程度。

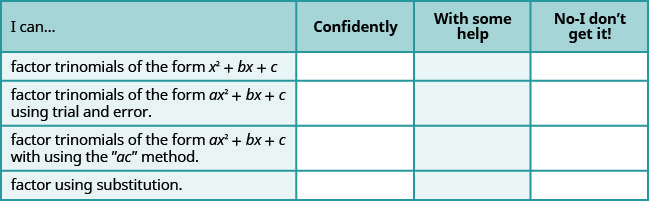
b. 看完这份清单后，你会怎么做才能对所有目标充满信心？