6.3: 因子三项式
- Page ID
- 203913
在本节结束时,您将能够:
- 形式的因子三项式\(x^2+bx+c\)
- \(ax^2+bx+c\)使用反复试验对形式的三项式进行分数
- \(ax^2+bx+c\)使用 '\(ac\)' 方法对形式的三项式进行因子分数
- 使用替换的因子
在开始之前,请参加这个准备测验。
形式的因子三项式\(x^2+bx+c\)
你已经学会了如何使用 FOIL 乘以二项式。 现在你需要 “撤消” 这个乘法。 分解三项式意味着从乘积开始,以因子结束。
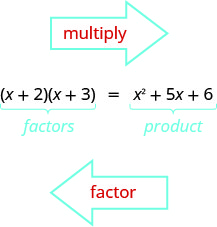
为了弄清楚我们将如何分解形态的三项式\(x^2+bx+c\),例如\(x^2+5x+6\)并将其分解为\((x+2)(x+3)\),让我们从两个形式\((x+m)\)和的通用二项式开始\((x+n)\)。
| \((x+m)(x+n)\) | |
| 用铝箔找到产品。 | \(x^{2}+m x+n x+m n\) |
| 将GCF从中间值中考虑在内。 | \(x^{2}+(m+n) x+m n\) |
| 我们的三项式是这样的\(x^2+bx+c\)。 | \(\overbrace{x^{2}+(m+n) x+m n}^{\color{red}x^{2}+b x+c}\) |
这告诉我们,要对形式的三项式进行分解\(x^2+bx+c\),我们需要两个因子\((x+m)\)\((x+n)\),两个数字\(m\)\(n\)相乘再相加\(b\)。\(c\)
因子:\(x^2+11x+24\)。
- 回答
-




因子:\(q^2+10q+24\)。
- 回答
-
\((q+4)(q+6)\)
因子:\(t^2+14t+24\)。
- 回答
-
\((t+2)(t+12)\)
让我们总结一下我们用来寻找因子的步骤。
- 将因子写成两个二项式,第一个项为 x。 \(\quad \begin{array} {l} x^2+bx+c \\ (x\quad)(x\quad) \end{array} \)
- 找两个数字\(m\)然后\(n\)那个
- 乘以\(c\),\(m·n=c\)
- 添加到\(b\),\(m+n=b\)
- 使用\(m\)和\(n\)作为因子的最后一个术语。 \(\quad (x+m)(x+n)\)
- 通过乘以因子进行检查。
在第一个例子中,三项式中的所有项均为正。 当有负数条件时会发生什么? 好吧,这取决于哪个术语是负数。 让我们先来看看只有中间项为负的三项式。
你如何得到正乘积和负和? 我们使用两个负数。
因子:\(y^2−11y+28\)。
- 回答
-
同样,鉴于上个学期为正值\(28\),中间为负值\(−11y\),我们需要两个负面因素。 找出两个相乘\(28\)和相加的数字\(−11\)。
\(\begin{array} {ll} &y^2−11y+28 \\ \text{Write the factors as two binomials with first terms }y. &( y \quad )( y \quad ) \\ \text{Find two numbers that: multiply to }28\text{ and add to }−11.\end{array}\)的因素\(28\) 因子总和 \ (28\)” data-valign= “top” >\(−1,\space −28\)
\(−2,\space −14\)
\(−4,\space −7\)\(−1+(−28)=−29\)
\(−2+(−14)=−16\)
\(−4+(−7)=−11^∗\)\(\begin{array} {ll} \text{Use }−4,\space −7\text{ as the last terms of the binomials.} &(y−4)(y−7) \\ \text{Check:} & \\ \hspace{30mm} (y−4)(y−7) & \\ \hspace{25mm} y^2−7y−4y+28 & \\ \hspace{30mm} y^2−11y+28\checkmark & \end{array} \)
因子:\(u^2−9u+18\)。
- 回答
-
\((u−3)(u−6)\)
因子:\(y^2−16y+63\)。
- 回答
-
\((y−7)(y−9)\)
现在,如果三项式中的最后一个项是负数呢? 想想 FO IL。 最后一个项是两个二项式中最后一个项的乘积。 将两个具有相反符号的数字相乘得出负乘积。 你必须非常谨慎地选择因素,以确保你也得到中间学期的正确符号。
你如何得到负乘积和正和? 我们使用一个正数和一个负数。
当我们分解三项式时,必须将术语按降序编写,即从最高度到最低的顺序排列。
因子:\(2x+x^2−48\)。
- 回答
-
\(\begin{array} {ll} &2x+x^2−48 \\ \text{First we put the terms in decreasing degree order.} &x^2+2x−48 \\ \text{Factors will be two binomials with first terms }x. &(x\quad)(x\quad) \end{array} \)
−48−48 的因子 因子总和 \(−1,\space 48\)
\(−2,\space 24\)
\(−3,\space 16\)
\(−4,\space 12\)
\(−6,\space 8\)\(−1+48=47\)
\(−2+24=22\)
\(−3+16=13\)
\(−4+12=8\)
\(−6+8=2^∗\)\(\begin{array} {ll} \text{Use }−6,\space 8\text{ as the last terms of the binomials.} &(x−6)(x+8) \\ \text{Check:} & \\ \hspace{30mm} (x−6)(x+8) & \\ \hspace{25mm} x^2−6q+8q−48 & \\ \hspace{30mm} x^2+2x−48\checkmark & \end{array} \)
因子:\(9m+m^2+18\)。
- 回答
-
\((m+3)(m+6)\)
因子:\(−7n+12+n^2\)。
- 回答
-
\((n−3)(n−4)\)
有时候你需要\(x^2+bxy+cy^2\)用两个变量对形式的三项式进行分解,例如\(x^2+12xy+36y^2\)。 第一个项是二项式因子的第一个项的乘积\(x·x\)。\(x^2\) 最后一个项\(y^2\)中的表示二项式因子的第二个项必须各包含\(y\)。 要获得系数\(b\)和\(c\),请使用如何分解三项式中总结的相同过程。
因子:\(r^2−8rs−9s^2\)。
- 回答
-
我们在每个二\(r\)项式的第一个项和第二个项\(s\)中都需要。 三项式的最后一个项是负数,因此因子必须具有相反的符号。
\(\begin{array} {ll} &r^2−8rs−9s^2 \\ \text{Note that the first terms are }r,\text{last terms contain }s. &(r\quad s)(r\quad s) \\ \text{Find the numbers that multiply to }−9\text{ and add to }−8. \end{array}\)的因素\(−9\) 因子总和 \ (−9\)” data-valign= “top” >\(1,\space −9\) \(−1+9=8\) \ (−9\)” data-valign= “top” >\(−1,\space 9\) \(1+(−9)=−8^∗\) \ (−9\)” data-valign= “top” >\(3,\space −3\) \(3+(−3)=0\) \(\begin{array} {ll} \text{Use }1,\space -9\text{ as coefficients of the last terms.} &(r+s)(r−9s) \\ \text{Check:} & \\ \hspace{30mm} (r−9s)(r+s) & \\ \hspace{25mm} r^2+rs−9rs−9s^2 & \\ \hspace{30mm} r^2−8rs−9s^2\checkmark & \end{array} \)
因子:\(a^2−11ab+10b^2\)。
- 回答
-
\((a−b)(a−10b)\)
因子:\(m^2−13mn+12n^2\)。
- 回答
-
\((m−n)(m−12n)\)
有些三项式是素数。 确定三项式是素数的唯一方法是列出所有可能性,并表明它们都不起作用。
因子:\(u^2−9uv−12v^2\)。
- 回答
-
我们在每个二\(u\)项式的第一个项和第二个项\(v\)中都需要。 三项式的最后一个项是负数,因此因子必须具有相反的符号。
\(\begin{array} {ll} &u^2−9uv−12v^2 \\ \text{Note that the first terms are }u,\text{ last terms contain }v. &(u\quad v)(u\quad v) \\ \text{Find the numbers that multiply to }−12\text{ and add to }−9. & \end{array} \)的因素\(−12\) 因子总和 \ (−12\)” data-valign= “top” >\(1,−12\)
\(−1,12\)
\(2,−6\)
\(−2,6\)
\(3,−4\)
\(−3,4\)\(1+(−12)=−11\)
\(−1+12=11\)
\(2+(−6)=−4\)
\(−2+6=4\)
\(3+(−4)=−1\)
\(−3+4=1\)请注意,没有因子对可以给\(−9\)出总和。 三项式是素数。
因子:\(x^2−7xy−10y^2\)。
- 回答
-
主要
因子:\(p^2+15pq+20q^2\)。
- 回答
-
主要
让我们总结一下我们刚刚开发的用于分解这种形式的三项式的方法\(x^2+bx+c\)。
当我们分解三项式时,我们首先看其项的符号,以确定二项式因子的符号。
| \( x^{2}+b x+c \) | ||
| \( (x+m)(x+n) \) | ||
| 何时\( c \)为正数\( n \),\( m \)且符号相同。 | ||
| \( b \)阳性 | \( b \)负面的 | |
| \( m,n \)阳性 | \( m,n \)负面的 | |
| \( x^{2}+5 x+6 \) | \( x^{2}-6 x+8 \) | |
| \( (x+2)(x+3) \) | \( (x-4)(x-2) \) | |
| 同样的迹象 | 同样的迹象 | |
| 何时\( c \)为负数,\( m \)且\( n \)具有相反的符号。 | ||
| \( x^{2}+x-12 \) | \( x^{2}-2 x-15 \) | |
| \( (x+4)(x-3) \) | \( (x-5)(x+3) \) | |
| 相反的迹象 | 相反的迹象 | |
请注意,在\(m\)和\(n\)具有相反符号的情况下,绝对值较大的符号与的符号匹配\(b\)。
使用反复试验的因子三项式 ax 2 + bx + c
我们的下一步是分解前导系数不是 1 的三项式,即形式的三项式\(ax^2+bx+c\)。
记得一定要先查看 GCF! 有时候,在你将 GCF 分解后,三项式的前导系数变成\(1\),你可以用我们到目前为止使用的方法对其进行分解。 让我们举个例子来看看它是如何工作的。
完全考虑因素:\(4x^3+16x^2−20x\).
- 回答
-
\(\begin{array} {lll} \text{Is there a greatest common factor?} &\qquad &4x^3+16x^2−20x \\ \quad \text{Yes, }GCF=4x.\text{ Factor it.} & &4x(x^2+4x−5) \\ & & \\ & & \\ \text{Binomial, trinomial, or more than three terms?} & & \\ \quad \text{It is a trinomial. So “undo FOIL.”} & &4x(x\quad)(x\quad) \\ & & \\ & & \\ \text{Use a table like the one shown to find two numbers that} & &4x(x−1)(x+5) \\ \text{multiply to }−5\text{ and add to }4. & & \\ & & \\ & & \end{array} \)
的因素\(−5\) 因子总和 \ (−5\)” data-valign= “top” >\(−1,5\)
\(1,−5\)\(−1+5=4^∗\)
\(1+(−5)=−4\)\(\begin{array} {l} \text{Check:}\\ \hspace{27mm}4x(x−1)(x+5) \\ \hspace{25mm} 4x(x^2+5x−x−5) \\ \hspace{30mm} 4x(x^2+4x−5) \\ \hspace{25mm} 4x^3+16x2−20x\checkmark \end{array} \)
完全考虑因素:\(5x^3+15x^2−20x\).
- 回答
-
\(5x(x−1)(x+4)\)
完全考虑因素:\(6y^3+18y^2−60y\).
- 回答
-
\(6y(y−2)(y+5)\)
当前导系数不是\(1\)且没有 GCF 时会发生什么? 有几种方法可以用来分解这些三项式。 首先,我们将使用 “反复试验” 方法。
让我们考虑三项式\(3x^2+5x+2\)。
根据我们之前的工作,我们预计这将分为两个二项式。
\[3x^2+5x+2\nonumber\]\[(\quad)(\quad)\nonumber\]
我们知道二项式因子的第一个项会乘以得出\(3x^2\)。 的唯一因素\(3x^2\)是\(1x,\space 3x\). 我们可以将它们放在二项式中。
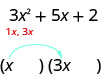
查看:是吗\(1x·3x=3x^2\)?
我们知道二项式的最后一项将乘以\(2\)。 由于这个三项式都有正项,我们只需要考虑正因素即可。 的唯一因素\(2\)是\(1\)和\(2\)。 但是我们现在有两个案例需要考虑,因为如果我们写\(2\)或\(1\)\(2\),会有所作为\(1\)。

哪些因素是正确的? 为了决定这一点,我们将内部和外部项相乘。
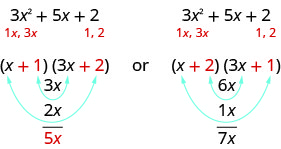
由于三项式的中间项是\(5x\),因此第一种情况中的因子将起作用。 让我们使用 FOIL 来检查一下。
\[(x+1)(3x+2)\nonumber\]\[3x^2+2x+3x+2\nonumber\]\[3x^2+5x+2\checkmark\nonumber\]
我们的保理结果是:
\[3x^2+5x+2\nonumber\]\[(x+1)(3x+2)\nonumber\]
使用反复试验完全考虑因素:\(3y^2+22y+7\).
- 回答
-






使用反复试验完全考虑因素:\(2a^2+5a+3\).
- 回答
-
\((a+1)(2a+3)\)
使用反复试验完全考虑因素:\(4b^2+5b+1\).
- 回答
-
\((b+1)(4b+1)\)
形式的@@
- 根据需要按度数的降序写出三项式。
- 将任何 GCF 考虑在内。
- 找出第一个项的所有因子对。
- 找出第三项的所有因子对。
- 测试所有可能的因子组合,直到找到正确的乘积。
- 乘法检查。
请记住,当中间项为负数而最后一个项为正时,二项式中的符号必须均为负数。
使用反复试验完全考虑因素:\(6b^2−13b+5\).
- 回答
-
三项式已经按降序排列了。 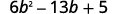
找出第一个术语的因素。 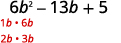
找出最后一个学期的因素。 考虑一下这些迹象。
由于最后一个学期为正\(5\),其因子必须均为
正数或两者均为负数。
中间项的系数为负,因此我们使用负因子。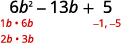
考虑所有因子组合。
\(6b^2−13b+5\) 可能的因素 产品 \ (6b^2−13b+5\) 可能的因素” data-valign= “top” >\((b−1)(6b−5)\) \ (6b^2−13b+5\) 产品” data-valign= “top” >\(6b^2−11b+5\) \ (6b^2−13b+5\) 可能的因素” data-valign= “top” >\((b−5)(6b−1)\) \ (6b^2−13b+5\) 产品” data-valign= “top” >\(6b^2−31b+5\) \ (6b^2−13b+5\) 可能的因素” data-valign= “top” >\((2b−1)(3b−5)\) \ (6b^2−13b+5\) 产品” data-valign= “middle” >\(6b^2−13b+5^∗\) \ (6b^2−13b+5\) 可能的因素” data-valign= “top” >\((2b−5)(3b−1)\) \ (6b^2−13b+5\) 产品” data-valign= “middle” >\(6b^2−17b+5\) \(\begin{array} {ll} \text{The correct factors are those whose product} & \\ \text{is the original trinomial.} &(2b−1)(3b−5) \\ \text{Check by multiplying:} & \\ \hspace{50mm} (2b−1)(3b−5) & \\ \hspace{47mm} 6b^2−10b−3b+5 & \\ \hspace{50mm} 6b^2−13b+5\checkmark & \end{array} \)
使用反复试验完全考虑因素:\(8x^2−14x+3\).
- 回答
-
\((2x−3)(4x−1)\)
使用反复试验完全考虑因素:\(10y^2−37y+7\).
- 回答
-
\((2y−7)(5y−1)\)
当我们对一个表达式进行分解时,我们总是首先寻找一个最大的共同因子。 如果表达式没有最大公因子,则其因子中也不能有最大公因子。 这可能有助于我们消除一些可能的因子组合。
使用反复试验完全考虑因素:\(18x^2−37xy+15y^2\).
- 回答
-
三项式已经按降序排列了。 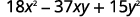
找出第一个术语的因素。 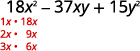
找出最后一个学期的因素。 考虑一下这些迹象。
由于 15 为正而中间
项系数为负,因此我们使用负因子。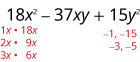
考虑所有因子组合。

\(\begin{array} {ll} \text{The correct factors are those whose product is} & \\ \text{the original trinomial.} &(2x−3y)(9x−5y) \\ \text{Check by multiplying:} & \\ & \\ & \\ & \\ \hspace{50mm} (2x−3y)(9x−5y) & \\ \hspace{45mm}18x^2−10xy−27xy+15y^2 & \\ \hspace{47mm}18x^2−37xy+15y^2\checkmark & \end{array} \)
使用反复试验完全考虑因素\(18x^2−3xy−10y^2\)。
- 回答
-
\((3x+2y)(6x−5y)\)
使用反复试验完全考虑因素:\(30x^2−53xy−21y^2\).
- 回答
-
\((3x+y)(10x−21y)\)
别忘了先寻找 GCF,记住前导系数是否为负,GCF 也是负数。
使用反复试验完全考虑因素:\(−10y^4−55y^3−60y^2\).
- 回答
-
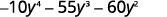
注意最大的共同因素,所以请先将其考虑在内。 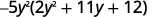
将三项式分解为因子。 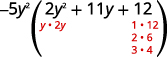
考虑所有的组合。
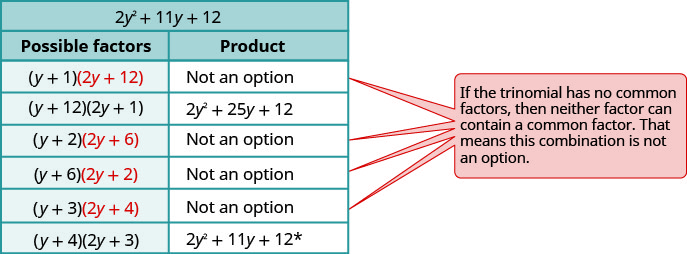
-
\(\begin{array} {ll} \text{The correct factors are those whose product} & \\ \text{is the original trinomial. Remember to include} & \\ \text{the factor }−5^y2. &−5y^2(y+4)(2y+3) \\ \text{Check by multiplying:} & \\ \hspace{50mm} −5y^2(y+4)(2y+3) & \\ \hspace{45mm} −5y^2(2y^2+8y+3y+12) & \\ \hspace{47mm}−10y^4−55y^3−60y^2\checkmark & \end{array} \)
使用反复试验完全考虑因素:\(15n^3−85n^2+100n\).
- 回答
-
\(5n(n−4)(3n−5)\)
使用反复试验完全考虑因素:\(56q^3+320q^2−96q\).
- 回答
-
\(8q(q+6)(7q−2)\)
\(ax^2+bx+c\)使用 “\(ac\)” 方法的形式因子三项式
分解这种形式的三项式的另一种方法\(ax^2+bx+c\)是 “\(ac\)” 方法。 (“\(ac\)” 方法有时称为分组方法。) “\(ac\)” 方法实际上是您在上一节中使用的方法的扩展,用于分解系数为前导系数为一的三项式。 这种方法非常结构化(即分步进行),并且始终有效!
使用 “\(ac\)” 方法的因子:\(6x^2+7x+2\).
- 回答
-






使用 “\(ac\)” 方法的因子:\(6x^2+13x+2\).
- 回答
-
\((x+2)(6x+1)\)
使用 “\(ac\)” 方法的因子:\(4y^2+8y+3\).
- 回答
-
\((2y+1)(2y+3)\)
这里总结\(ac\)了 “” 方法。
形式的@@
- 将任何 GCF 考虑在内。
- 找到产品\(ac\)。
- 找到两个数字\(m\)然后\(n\)那个:
\(\begin{array} {ll} \text{Multiply to }ac &m·n=a·c \\ \text{Add to }b &m+n=b \\ &ax^2+bx+c \end{array} \) - 使用\(m\)和拆分中间术语\(n\)。 \(ax^2+mx+nx+c\)
- 按分组进行因子排序。
- 通过乘以因子进行检查。
别忘了寻找一个共同的因素!
使用 '“\(ac\)” 方法进行因子:\(10y^2−55y+70\).
- 回答
-
有最大的共同因素吗? 是的。 全球气候基金是\(5\)。 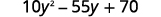
将其考虑在内。 
括号内的三项式的前
导系数不是\(1\)。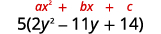
找到产品\(ac\)。 \(ac=28\) 找出两个相乘的数字\(ac\) \((−4)(−7)=28\) 并添加到\(b\)。 \(−4(−7)=−11\) 拆分中间学期。 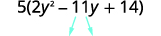
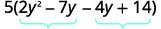
通过分组对三项式进行分解。 
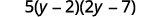
将所有三个因子相乘进行检查。
\(\hspace{50mm} 5(y−2)(2y−7)\)\(\hspace{45mm} 5(2y^2−7y−4y+14)\)
\(\hspace{48mm} 5(2y^2−11y+14)\)
\(\hspace{49mm} 10y^2−55y+70\checkmark\)
使用 “\(ac\)” 方法的因子:\(16x^2−32x+12\).
- 回答
-
\(4(2x−3)(2x−1)\)
使用 “\(ac\)” 方法的因子:\(18w^2−39w+18\).
- 回答
-
\(3(3w−2)(2w−3)\)
使用替代的因子
有时,三项式似乎不是这种\(ax^2+bx+c\)形式。 但是,我们通常可以进行深思熟虑的替换,使我们能够使其符合\(ax^2+bx+c\)形式。 这称为替换分解。 使用它作为替\(u\)换是标准配置。
在中\(ax^2+bx+c\),中间项有一个变量\(x\),其平方是第一个项的可变部分。\(x^2\) 当你尝试寻找替代品时,请寻找这种关系。
替代因子:\(x^4−4x^2−5\).
- 回答
-
中间项的可变部分是\(x^2\)\(x^4\),其平方是第一个项的可变部分。 (我们知道\((x^2)^2=x^4)\)。 如果我们允\(u=x^2\)许,我们可以将我们的三项式转换为需要分解的\(ax^2+bx+c\)形式。
\(x^4−4x^2−5\) 重写三项式为替换做准备。 \((x^2)^2−4(x^2)-5\) 让我们\(u=x^2\)替换。 \((u)^2−4(u)-5\) 将三项式分解为因子。 \((u+1)(u-5)\) 替换\(u\)为\(x^2\)。 \((x^2+1)(x^2-5)\) 查看:
\(\begin{array} {l} \hspace{37mm} (x^2+1)(x^2−5) \\ \hspace{35mm}x^4−5x^2+x^2−5 \\ \hspace{40mm}x^4−4x^2−5\checkmark\end{array}\)
替代因子:\(h^4+4h^2−12\).
- 回答
-
\((h^2−2)(h^2+6)\)
替代因子:\(y^4−y^2−20\).
- 回答
-
\((y^2+4)(y^2−5)\)
有时要替换的表达式不是单项式。
替代因子:\((x−2)^2+7(x−2)+12\)
- 回答
-
中间项的二项式在第一个项中\((x−2)\)是平方。 如果我们让\(u=x−2\)和替换,我们的三项式就会\(ax^2+bx+c\)形成形式。
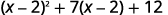
重写三项式为替换做准备。 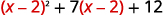
让我们\(u=x−2\)替换。 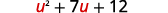
将三项式分解为因子。 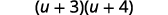
替换\(u\)为\(x−2\)。 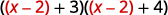
在圆括号内进行简化。 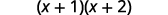
这也可以通过先乘以和然后合并相似项\((x−2)^2\)\(7(x−2)\)然后再进行分解来计算。 大多数学生更喜欢替代方法。
替代因子:\((x−5)^2+6(x−5)+8\).
- 回答
-
\((x−3)(x−1)\)
替代因子:\((y−4)^2+8(y−4)+15\).
- 回答
-
\((y−1)(y+1)\)
观看此视频,了解有关保理的更多指导和实践。
关键概念
- 如何分解形式的三项式\(x^2+bx+c\)。
- 将因子写成两个二项式,第一个项为 x。 \(\quad \begin{array} (l) x^2+bx+c \\ (x\quad)(x\quad)\end{array}\)
- 找两个数字\(m\)然后\(n\)那个
\(\begin{array} {ll} \text{multiply to} &c,\space m·n=c \\ \text{add to} &b,\space m+n=b\end{array}\) - 使用\(m\)和\(n\)作为因子的最后一个术语。 \(\qquad (x+m)(x+n)\)
- 通过乘以因子进行检查。
- 分解形式三项式的策略\(x^2+bx+c\):当我们分解三项式时,我们首先看其项的符号,以确定二项式因子的符号。
对于以下形式的三项式:\(x^2+bx+c = (x+m)(x+n)\)
W hen 为\(c\)正数,\(m\)并且\(n\)必须具有相同的符号(这将是\(b\))。
示例:\(x^2+5x+6=(x+2)(x+3)\),W\(x^2−6x+8 = (x−4)(x−2)\)
hen\(c\) 为负数,\(m\)且\(n\)具有相反的符号。 \(m\)和\(n\)中较大的符号为\(b\)。
示例:\(x^2+x−12=(x+4)(x−3)\),\(x^2−2x−15=(x−5)(x+3)\)
请注意,在\(m\)和\(n\)具有相反符号的情况下,绝对值较大的符号与的符号匹配\(b\)。 - 如何\(ax^2+bx+c\)使用反复试验来分解表格的三项式。
- 根据需要按度数的降序写出三项式。
- 将任何 GCF 考虑在内。
- 找出第一个项的所有因子对。
- 找出第三项的所有因子对。
- 测试所有可能的因子组合,直到找到正确的乘积。
- 乘法检查。
- 如何\(ax^2+bx+c\)使用 “\(ac\)” 方法分解形式的三项式。
- 将任何 GCF 考虑在内。
- 找到产品\(ac\)。
- 找到两个数字\(m\)然后\(n\)那个:
\(\begin{array} {ll} \text{Multiply to }ac. &m·n=a·c \\ \text{Add to }b. &m+n=b \\ &ax^2+bx+c\end{array}\) - 使用\(m\)和拆分中间术语\(n\)。 \(\quad ax^2+mx+nx+c\)
- 按分组进行因子排序。
- 通过乘以因子进行检查。


