5.5E：练习

Last updated
Save as PDF

Page ID: 203910

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\dsum}{\displaystyle\sum\limits} $

$ \newcommand{\dint}{\displaystyle\int\limits} $

$ \newcommand{\dlim}{\displaystyle\lim\limits} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$\newcommand{\longvect}{\overrightarrow}$

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

练习成就完美

划分单项式

在以下练习中，将单项式分开。

1。 $15r^4s^9÷(15r^4s^9)$

2。 $20m^8n^4÷(30m^5n^9)$

回答: $\dfrac{2m^3}{3n^5}$

3。 $\dfrac{18a^4b^8}{−27a^9b^5}$

4。 $\dfrac{45x^5y^9}{−60x^8y^6}$

回答: $\dfrac{−3y^3}{4x^3}$

5。 $\dfrac{(10m^5n^4)(5m^3n^6)}{25m^7n^5}$

6。 $\dfrac{(−18p^4q^7)(−6p^3q^8)}{−36p^{12}q^{10}}$

回答: $\dfrac{−3q^5}{p^5}$

7。 $\dfrac{(6a^4b^3)(4ab^5)}{(12a^2b)(a^3b)}$

8。 $\dfrac{(4u^2v^5)(15u^3v)}{(12u^3v)(u^4v)}$

回答: $\dfrac{5v^4}{u^2}$

将多项式除以单项式

在以下练习中，将每个多项式除以单项式。

9。 $(9n^4+6n^3)÷3n$

10。 $(8x^3+6x^2)÷2x$

回答: $4x^2+3x$

11。 $(63m^4−42m^3)÷(−7m^2)$

12。 $(48y^4−24y^3)÷(−8y^2)$

回答: $−6y^2+3y$

13。 $\dfrac{66x^3y^2−110x^2y^3−44x^4y^3}{11x^2y^2}$

14。 $\dfrac{72r^5s^2+132r^4s^3−96r^3s^5}{12r^2s^2}$

回答: $6r^3+11r^2s−8rs^3$

15。 $10x^2+5x−4−5x$

16。 $20y^2+12y−1−4y$

回答: $−5y−3+\dfrac{1}{4y}$

使用长除法将多项式除法

在以下练习中，将每个多项式除以二项式。

17。 $(y^2+7y+12)÷(y+3)$

18。 $(a^2−2a−35)÷(a+5)$

回答: $a−7$

19。 $(6m^2−19m−20)÷(m−4)$

20。 $(4x^2−17x−15)÷(x−5)$

回答: $4x+3$

21。 $(q^2+2q+20)÷(q+6)$

22。 $(p^2+11p+16)÷(p+8)$

回答: $p+3−\dfrac{8}{p+8}$

23。 $(3b^3+b^2+4)÷(b+1)$

24。 $(2n^3−10n+28)÷(n+3)$

回答: $\dfrac{2n^2−6n+8+4}{n+3}$

25。 $(z^3+1)÷(z+1)$

26。 $(m^3+1000)÷(m+10)$

回答: $m^2−10m+100$

27。 $(64x^3−27)÷(4x−3)$

28。 $(125y^3−64)÷(5y−4)$

回答: $25y^2+20x+16$

使用合成除法对多项式进行分割

在以下练习中，使用合成除法求商和余数。

29。 $x^3−6x^2+5x+14$除以$x+1$

30。 $x^3−3x^2−4x+12$除以$x+2$

回答: $x^2−5x+6; \space 0$

31。 $2x^3−11x^2+11x+12$除以$x−3$

32。 $2x^3−11x^2+16x−12$除以$x−4$

回答: $2x^2−3x+4; \space 4$

33。 $x^4-5x^2+2+13x+3$除以$x+3$

34。 $x^4+x^2+6x−10$除以$x+2$

回答: $x^3−2x^2+5x−4; \space −2$

35。 $2x^4−9x^3+5x^2−3x−6$除以$x−4$

36。 $3x^4−11x^3+2x^2+10x+6$除以$x−3$

回答: $3x^3−2x^2−4x−2;\space 0$

除以多项式函数

在以下练习中，除以。

37。对于函数$f(x)=x^2−13x+36$和$g(x)=x−4$，请查找 ⓐ$\left(\dfrac{f}{g}\right)(x)$ ⓑ$\left(\dfrac{f}{g}\right)(−1)$

38。对于函数$f(x)=x^2−15x+54$和$g(x)=x−9$，请查找 ⓐ$\left(\dfrac{f}{g}\right)(x)$ ⓑ$\left(\dfrac{f}{g}\right)(−5)$

回答: ⓐ$\left(\dfrac{f}{g}\right)(x)=x−6$
ⓑ$\left(\dfrac{f}{g}\right)(−5)=−11$

39。对于函数$f(x)=x^3+x^2−7x+2$和$g(x)=x−2$，请查找 ⓐ$\left(\dfrac{f}{g}\right)(x)$ ⓑ$\left(\dfrac{f}{g}\right)(2)$

40。对于函数$f(x)=x^3+2x^2−19x+12$和$g(x)=x−3$，请查找 ⓐ$\left(\dfrac{f}{g}\right)(x)$ ⓑ$\left(\dfrac{f}{g}\right)(0)$

回答: ⓐ$\left(\dfrac{f}{g}\right)(x)=x^2+5x−4$
ⓑ$\left(\dfrac{f}{g}\right)(0)=−4$

41。对于函数$f(x)=x^2−5x+2$和$g(x)=x^2−3x−1$，请查找 ⓐ$(f·g)(x)$ ⓑ$(f·g)(−1)$

42。对于函数$f(x)=x^2+4x−3$和$g(x)=x^2+2x+4$，请查找 ⓐ$(f·g)(x)$ ⓑ$(f·g)(1)$

回答: ⓐ$(f·g)(x)=x^4+6x^3+9x^2+10x−12$; ⓑ$(f·g)(1)=14$

使用余数和因子定理

在以下练习中，使用余数定理求余数。

43。 $f(x)=x^3−8x+7$除以$x+3$

44。 $f(x)=x^3−4x−9$除以$x+2$

回答: $−9$

45。 $f(x)=2x^3−6x−24$除以$x−3$

46。 $f(x)=7x^2−5x−8$除以$x−1$

回答: $−6$

在以下练习中，使用因子定理来确定 x−cx−c 是否是多项式函数的因子。

47。确定系$x+3$数是否为$x^3+8x^2+21x+18$

48。确定系$x+4$数是否为$x^3+x^2−14x+8$

回答: 不

49。确定系$x−2$数是否为$x^3−7x^2+7x−6$

50。确定系$x−3$数是否为$x^3−7x^2+11x+3$

回答: 是的

写作练习

51。詹姆斯$6$这样$48y+6$划分:$\dfrac{48y+6}{6}=48y$. 他的推理有什么问题？

52。划分$\dfrac{10x^2+x−12}{2x}$并用文字解释你是如何得到每个商项的。

回答: 答案会有所不同

53。解释何时可以使用合成除法。

54。用你自己的话说，写下合成$x^2+5x+6$除以的步骤$x−2$。

回答: 答案会有所不同。

自检

a. 完成练习后，使用此清单评估你对本节目标的掌握程度

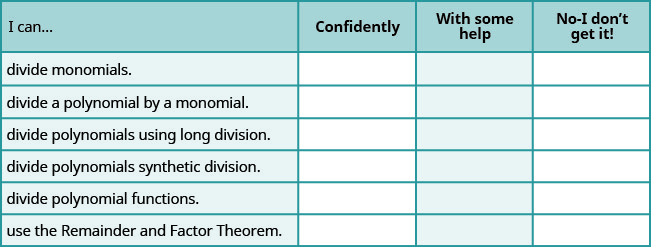
$该图显示了一个包含七行四列的表。第一行是标题行，它标记了每列。第一列标题是 “我能...”，第二列是 “自信地”，第三列是 “有帮助”，“不减去我不明白！”。第一列下方是 “除以单项式”、“使用单项式除以多项式”、“使用长除法除多项式”、“使用合成除法除多项式”、“除多项式函数” 和 “使用余数和因子定理” 等短语。在第二、第三、第四列下方是空格，学员可以在其中查看自己达到了什么程度的掌握程度。$

b. 在 1-10 分中，根据你在清单上的回答，你会如何评价你对本节的掌握程度？你怎么能改善这个？