5.5: 除以多项式
- Page ID
- 203907
在本节结束时,您将能够:
- 分割单项式
- 将多项式除以单项式
- 使用长除法除以多项式
- 使用合成除法分割多项式
- 除法多项式函数
- 使用余数和因子定理
在开始之前,请参加这个准备测验。
划分单项式
我们现在已经熟悉了指数的所有属性,并用它们来乘以多项式。 接下来,我们将使用这些属性来划分单项式和多项式。
找到商:\(54a^2b^3÷ (−6ab^5)\).
解决方案
当我们用多个变量除以单项式时,我们为每个变量写一个分数。
\(\begin{array} {ll} {} &{54a^2b^3÷(−6ab^5)} \\[5pt] {\text{Rewrite as a fraction.}} &{\dfrac{54a^2b^3}{−6ab^5}} \\[5pt] {\text{Use fraction multiplication.}} &{\dfrac{54}{−6}·\dfrac{a^2}{a}·\dfrac{b^3}{b^5}} \\[5pt] {\text{Simplify and use the Quotient Property.}} &{−9·a·\dfrac{1}{b^2}} \\[5pt] {\text{Multiply.}} &{−\dfrac{9a}{b^2}} \end{array}\)
找到商:\(−72a^7b^3÷(8a^{12}b^4)\).
- 回答
-
\(−\dfrac{9}{a^5b}\)
找到商:\(−63c^8d^3÷(7c^{12}d^2)\).
- 回答
-
\(\dfrac{−9d}{c^4}\)
一旦你熟悉了这个过程并逐步练习了好几次,你也许可以一步简化一小部分。
找到商:\(\dfrac{14x^7y^{12}}{21x^{11}y^6}\).
解决方案
要非常小心,\(\dfrac{14}{21}\)通过除去一个公共因子来简化变量,并通过减去它们的指数来简化变量。
\(\begin{array} {ll} {} &{\dfrac{14x^7y^{12}}{21x^{11}y^6}} \\ {\text{Simplify and use the Quotient Property.}} &{\dfrac{2y^6}{3x^4}} \\ \end{array}\)
找到商:\(\dfrac{28x^5y^{14}}{49x^9y^{12}}\).
- 回答
-
\(\dfrac{4y^2}{7x^4}\)
找到商:\(\dfrac{30m^5n^{11}}{48m^{10}n^{14}}\).
- 回答
-
\(\dfrac{5}{8m^5n^3}\)
将多项式除以单项式
既然我们已经知道如何将单项式除以单项式,接下来的步骤是将两个或更多项的多项式除以单项式。 我们将使用将多项式除以单项式的方法基于分数加法的属性。 因此,我们将从一个示例开始,回顾分数加法。 总和\(\dfrac{y}{5}+\dfrac{2}{5}\)简化为\(\dfrac{y+2}{5}\)。 现在我们将反向执行此操作,将单个分数拆分为单独的分数。 例如,\(\dfrac{y+2}{5}\)可以写入\(\dfrac{y}{5}+\dfrac{2}{5}\)。
这是分数加法的 “反向”,它指出,如果 a、b 和 c 是数字\(c\neq 0\),那么\(\dfrac{a+b}{c}=\dfrac{a}{c}+\dfrac{b}{c}\)。 我们将用它来将多项式除以单项式。
要将多项式除以单项式,请将多项式的每个项除以单项式。
找到商:\((18x^3y−36xy^2)÷(−3xy)\).
解决方案
\(\begin{array} {ll} {} &{(18x^3y−36xy^2)÷(−3xy)} \\[5pt] {\text{Rewrite as a fraction.}} &{\dfrac{18x^3y−36xy^2}{−3xy}} \\[5pt] {\text{Divide each term by the divisor. Be careful with the signs!}} &{\dfrac{18x^3y}{−3xy}−\dfrac{36xy^2}{−3xy}} \\[5pt] {\text{Simplify.}} &{−6x^2+12y} \end{array}\)
找到商:\((32a^2b−16ab^2)÷(−8ab)\).
- 回答
-
\(−4a+2b\)
找到商:\((−48a^8b^4−36a^6b^5)÷(−6a^3b^3)\).
- 回答
-
\(8a^5b+6a^3b^2\)
使用长除法除以多项式
将多项式除以二项式,我们遵循的过程与数字的长除法非常相似。 因此,让我们仔细看看我们将 3 位数的数字 875 除以 2 位数 25 时所采取的步骤。
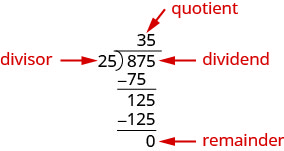
我们通过将商乘以除数来检查除法。 如果我们正确地进行了分割,则该乘积应等于分红。
\[\begin{array} {l} {35·25} \\ {875\checkmark} \\ \nonumber \end{array}\]
现在我们将三项式除以二项式。 在通读示例时,请注意这些步骤与上面的数字示例有多相似。
找到商:\((x^2+9x+20)÷(x+5)\).
解决方案
| \(\require{enclose}\) | \(\qquad (x^2+9x+20) \div (x+5)\) |
| 把它写成一个长分割问题。 确保分红是标准形式。 |
\(\qquad x+5\enclose{longdiv}{ x^2+9x+20\phantom{0}} \) |
|
除\(x^2\)以\(x\)。 问问自己:“我需要\(x\)乘以什么才能得 |
\(\qquad \begin{array}{r} {\color{red}x}\hspace{2.3em}\\[-3pt] {\color{red}x}+5\enclose{longdiv}{ {\color{red}x^2}+9x+20\phantom{0}} \end{array}\) |
| 将答案放在\(x\)术语的商数中。\(x\) \(x\)乘以\(x+5\)。 在分红下排列类似条款。 |
\(\qquad \begin{array}{r}x\hspace{2.3em}\\[-3pt] x+5\enclose{longdiv}{x^2+9x+20\phantom{0}}\\[-3pt] \underline{\color{red}x^2+5x}\hspace{2.4em} \end{array}\) |
| \(x^2+5x\)从... 中减去\(x^2+9x\)。 您可能会发现更改符号然后添加更容易。 然后把最后一个学期放下,\(20.\) |
\(\qquad \begin{array}{r}x\hspace{2.3em}\\[-3pt] x+5\enclose{longdiv}{x^2+\phantom{00}9x+20\phantom{0}}\\[-3pt] \underline{{\color{red}-}x^2+({\color{red}-}5x)}\hspace{2.1em}\\[-3pt] {\color{red}4x+20}\hspace{0.5em} \end{array}\) |
除\(4x\)以\(x\)。 问问自己:“我 需要\(x\)乘以什么才能得到\(4x\)?” 可能会有所帮助 将答案放在常量项的商中。\(4\) |
\(\qquad \begin{array}{r}x+\phantom{0}{\color{red}4}\hspace{.5em}\\[-3pt] {\color{red}x}+5\enclose{longdiv}{x^2+\phantom{00}9x+20\phantom{0}}\\[-3pt] \underline{{\color{red}-}x^2+({\color{red}-}5x)}\hspace{2.1em}\\[-3pt] {\color{red}4x}+20\hspace{0.5em} \end{array}\) |
| 乘以 4 次\(x+5\)。 |
\(\qquad \begin{array}{r}x+\phantom{0}4\hspace{.5em}\\[-3pt] x+5\enclose{longdiv}{x^2+\phantom{00}9x+20\phantom{0}}\\[-3pt] \underline{{\color{red}-}x^2+({\color{red}-}5x)}\hspace{2.1em}\\[-3pt] 4x+20\hspace{0.5em}\\[-3pt] \underline{ \color{red}4x+20}\hspace{.5em} \end{array}\) |
| \(4x+20\)从... 中减去\(4x+20\)。 |
\(\qquad \begin{array}{r}x+\phantom{0}4\hspace{.5em}\\[-3pt] x+5\enclose{longdiv}{x^2+\phantom{00}9x+20\phantom{0}}\\[-3pt] \underline{{\color{red}-}x^2+({\color{red}-}5x)}\hspace{2.1em}\\[-3pt] 4x+20\hspace{.5em}\\[-3pt] \underline{{\color{red}-}4x+({\color{red}-}20)}\\[-3pt] 0\hspace{.33em}\end{array}\) |
|
查看: \(\begin{array} {ll} {\text{Multiply the quotient by the divisor.}} &{(x+4)(x+5)} \\ {\text{You should get the dividend.}} &{x^2+9x+20\checkmark}\\ \end{array}\) |
找到商:\((y^2+10y+21)÷(y+3)\).
- 回答
-
\(y+7\)
找到商:\((m^2+9m+20)÷(m+4)\).
- 回答
-
\(m+5\)
当我们将 875 除以 25 时,我们没有余数。 但是有时候数字的除法确实会留下余数。 当我们分割多项式时也是如此。 在下一个例子中,我们将得到一个除法,剩下余数。 我们将余数写成分数,以除数作为分母。
回过头来看看前面例子中的分红。 这些术语按学位降序编写,没有缺失学位。 此示例中的分红将为\(x^4−x^2+5x−6\)。 它缺少一个\(x^3\)术语。 我们将添加\(0x^3\)为占位符。
找到商:\((x^4−x^2+5x−6)÷(x+2)\).
解决方案
请注意,分红中没有\(x^3\)期限。 我们将添加\(0x^3\)为占位符。
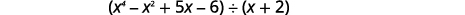 |
|
| 把它写成一个长分割问题。 确保分红采用标准形式,并带有缺失条款的占位符。 | 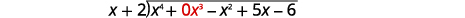 |
| 除\(x^4\)以\(x\)。 将答案放在\(x^3\)术语的商数中。\(x^3\) \(x^3\)乘以\(x+2\)。 用相似的术语排成一列。 减去然后降低下一个学期。 |
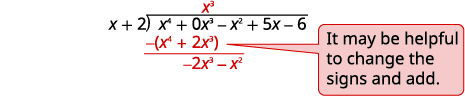 |
| 除\(−2x^3\)以\(x\)。 将答案放在\(x^2\)术语的商数中。\(−2x^2\) \(−2x^2\)乘以\(x+1\)。 将类似的术语排成 减去然后降低下一个学期。 |
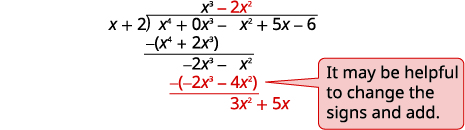 |
| 除\(3x^2\)以\(x\)。 将答案放在\(x\)术语的商数中。\(3x\) \(3x\)乘以\(x+1\)。 用相似的术语排成一列。 减去并降低下一个学期。 |
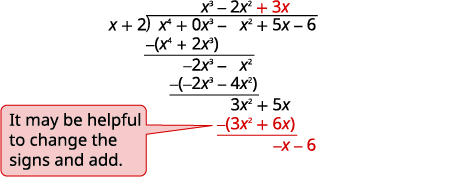 |
| 除\(−x\)以\(x\)。 将答案放在常量项的商中。\(−1\) \(−1\)乘以\(x+1\)。 用相似的术语排成一列。 更改标志,添加。 将余数写成分数,以除数作为分母。 |
 |
| 要检查,请乘以\((x+2)(x^3−2x^2+3x−1−4x+2)\)。 结果应该是\(x^4−x^2+5x−6\)。 |
找到商:\((x^4−7x^2+7x+6)÷(x+3)\).
- 回答
-
\(x^3−3x^2+2x+1+3x+3\)
找到商:\((x^4−11x^2−7x−6)÷(x+3)\).
- 回答
-
\(x^3−3x^2−2x−1−3x+3\)
在下一个示例中,我们将除以\(2a−3\)。 当我们进行划分时,我们必须考虑常量和变量。
找到商:\((8a^3+27)÷(2a+3)\).
解决方案
这次我们将一步展示所有分区。 我们需要添加两个占位符才能进行划分。
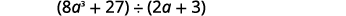 |
|
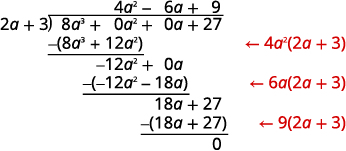 |
要检查,请乘以\((2a+3)(4a^2−6a+9)\)。
结果应该是\(8a^3+27\)。
找到商:\((x^3−64)÷(x−4)\).
- 回答
-
\(x^2+4x+16\)
找到商:\((125x^3−8)÷(5x−2)\).
- 回答
-
\(25x^2+10x+4\)
使用合成除法划分多项式
正如我们之前提到的,数学家喜欢寻找模式来简化他们的工作。 由于长分割可能很乏味,让我们回顾一下我们在示例中所做的长分割并寻找一些模式。 我们将以此为基础进行所谓的合成分割。 合成除法格式中的相同问题如下所示。
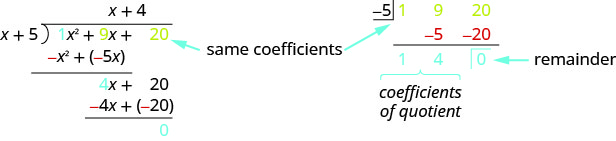
合成除法基本上只是删除不必要的重复变量和数字。 这里所有的\(x\)和\(x^2\)都被删除了。以及\(−x^2\)和\(−4x\)因为它们与上面的术语相反。
- 合成除法的第一行是分红系数。 与\(−5\)除数中的 5 相反。
- 合成除法的第二行是除法问题中以红色显示的数字。
- 合成除法的第三行是除法问题中以蓝色显示的数字。
请注意,商数和余数显示在第三行中。
\[\text{Synthetic division only works when the divisor is of the form }x−c. \nonumber \]
以下示例将解释该过程。
当除以时\(2x^3+3x^2+x+8\),使用合成除法求商和余数\(x+2\)。
解决方案
| 用递减的幂写下股息\(x\)。 | 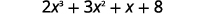 |
| 将项的系数写成合成除法的第一 行。 |
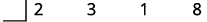 |
| 将除数写为,\(x−c\)然后将 c 放在除数框的合成除数中。 |
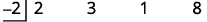 |
| 将第一个系数降低到第三行。 | 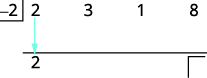 |
| 将该系数乘以除数,然后将 结果放在第二行第二个系数之下。 |
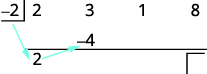 |
| 添加第二列,将结果放在第三行。 | 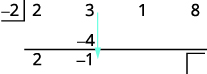 |
| 将该结果乘以除数,然后将 结果放在第二行第三个系数之下。 |
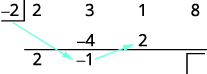 |
| 添加第三列,将结果放在第三行。 | 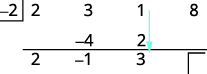 |
| 将该结果乘以除数,然后将 结果放在第三行第三个系数之下。 |
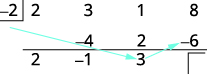 |
| 添加最后一列,将结果放在第三行。 | 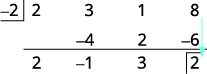 |
| 商为\(2x^2−1x+3\),余数为 2。 |
分割已完成。 第三行中的数字给出了结果。 \(2\space\space\space−1\space\space\space3\)它们是商的系数。 商是\(2x^2−1x+3\)。 第三行方框中的 2 是余数。
查看:
\(\begin{align} (\text{quotient})(\text{divisor}) + \text{remainder} &= \text{dividend} \nonumber\\ (2x^2−1x+3)(x+2)+2 &\overset{?}{=} 2x^3+3x^2+x+8 \nonumber\\ 2x^3−x^2+3x+4x^2−2x+6+2 &\overset{?}{=} 2x^3+3x^2+x+8 \nonumber\\ 2x^3+3x^2+x+8 &= 2x^3+3x^2+x+8\checkmark \nonumber \end{align} \)
当除以时\(3x^3+10x^2+6x−2\),使用合成除法求商和余数\(x+2\)。
- 回答
-
\(3x^2+4x−2;\space 2\)
当除以时\(4x^3+5x^2−5x+3\),使用合成除法求商和余数\(x+2\)。
- 回答
-
\(4x^2−3x+1; 1\)
在下一个示例中,我们将一起完成所有步骤。
当除以时\(x^4−16x^2+3x+12\),使用合成除法求商和余数\(x+4\)。
解决方案
多项式的\(x^4−16x^2+3x+12\)项按降序排列,但我们注意到没有\(x^3\)项。 我们将添加 0 作为该\(x^3\)术语的占位符。 \(x−c\)形式上,除数是\(x−(−4)\)。
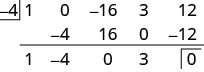
我们将\(4^{\text{th}}\)度数多项式除以\(1^{\text{st}}\)度数多项式,因此商将为\(3^{\text{rd}}\)度多项式。
从第三行读取,商有系数\(1\space\space\space−4\space\space\space0\space\space\space3\),也就是说\(x^3−4x^2+3\)。 余数
为 0。
当除以时\(x^4−16x^2+5x+20\),使用合成除法求商和余数\(x+4\)。
- 回答
-
\(x^3−4x^2+5;\space 0\)
当除以时\(x^4−9x^2+2x+6\),使用合成除法求商和余数\(x+3\)。
- 回答
-
\(x^3−3x^2+2;\space 0\)
除以多项式函数
正如多项式可以分割一样,多项式函数也可以分割。
对于函数\(f(x)\)\(g(x)\),在哪里\(g(x)\neq 0\),
\[\left(\dfrac{f}{g}\right)(x)=\dfrac{f(x)}{g(x)} \nonumber\]
对于函数\(f(x)=x^2−5x−14\)和\(g(x)=x+2\),请查找:
- \(\left(\dfrac{f}{g}\right)(x)\)
- \(\left(\dfrac{f}{g}\right)(−4)\)。
解决方案
ⓐ
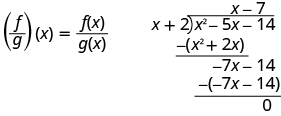
\(\begin{array} {ll} {\text{Substitute for }f(x)\text{ and }g(x).} &{\left(\dfrac{f}{g}\right)(x)=\dfrac{x^2−5x−14}{x+2}} \\[5pt] {\text{Divide the polynomials.}} &{\left(\dfrac{f}{g}\right)(x)=x−7} \end{array} \)
ⓑ 部分 ⓐ 我们找到了\(\left(\dfrac{f}{g}\right)(x)\),现在被要求去找\(\left(\dfrac{f}{g}\right)(−4)\)。
\(\begin{array} {ll} {} &{\left(\dfrac{f}{g}\right)(x)=x−7} \\[5pt] {\text{To find }\left(\dfrac{f}{g}\right)(−4), \text{ substitute }x=−4.} &{\left(\dfrac{f}{g}\right)(−4)=−4−7} \\[5pt] {} &{\left(\dfrac{f}{g}\right)(−4)=−11} \end{array}\)
对于函数\(f(x)=x^2−5x−24\)和\(g(x)=x+3\),请查找:
- \(\left(\dfrac{f}{g}\right)(x)\)
- \(\left(\dfrac{f}{g}\right)(−3)\)。
- 回答 a
-
\(\left(\dfrac{f}{g}\right)(x)=x−8\)
- 答案 b
-
\(\left(\dfrac{f}{g}\right)(−3)=−11\)
对于函数\(f(x)=x2−5x−36\)和\(g(x)=x+4\),请查找:
- \(\left(\dfrac{f}{g}\right)(x)\)
- \(\left(\dfrac{f}{g}\right)(−5)\)。
- 回答 a
-
\(\left(\dfrac{f}{g}\right)(x)=x−9\)
- 答案 b
-
\(\left(\dfrac{f}{g}\right)(x)=x−9\)
使用余数和因子定理
让我们来看一下我们刚刚解决的分区问题,这些问题最终都剩下了。 它们汇总在下表中。 如果我们从每个除法问题中取出分红并用它来定义一个函数,我们就会得到图表中显示的函数。 当除数写成时\(x−c\),函数 at\(c\) 的值与除法问题的余数相同。\(f(c)\)
| 分红 | 除数\(x−c\) | 剩余部分 | 函数 | \(f(c)\) |
|---|---|---|---|---|
| \(x^4−x^2+5x−6\) | \ (x−c\)” data-valign= “top” >\(x−(−2)\) | \(−4\) | \(f(x)=x^4−x^2+5x−6\) | \ (f (c)\)” data-valign= “top” >\(−4\) |
| \(3x^3−2x^2−10x+8\) | \ (x−c\)” data-valign= “top” >\(x−2\) | 4 | \(f(x)=3x^3−2x^2−10x+8\) | \ (f (c)\)” data-valign= “top” >4 |
| \(x^4−16x^2+3x+15\) | \ (x−c\)” data-valign= “top” >\(x−(−4)\) | 3 | \(f(x)=x^4−16x^2+3x+15\) | \ (f (c)\)” data-valign= “top” >3 |
为了更笼统地看待这个问题,我们意识到我们可以通过将商乘以除数然后将余数相加来检查除法问题。 在函数表示法中,我们可以说\(f(x)\),为了得到分红,我们将商乘以除数\(x−c\),然后将余数相加\(r\)。\(q(x)\)
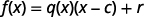 |
|
| 如果我们对此进行评估\(c\),我们会得到: | 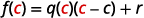 |
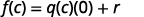 |
|
 |
这就引出了余数定理。
如果多项式函数\(f(x)\)除以\(x−c\),则余数为\(f(c)\)。
当除以时,使用余数定理\(f(x)=x^3+3x+19\)求余数\(x+2\)。
解决方案
要使用余数定理,我们必须使用\(x−c\)表单中的除数。 我们可以将除数写\(x+2\)成\(x−(−2)\)。 所以,我们\(c\)是\(−2\)。
为了找到余数,我们评估\(f(c)\)哪个是\(f(−2)\)。
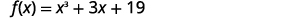 |
|
| 要进行评估\(f(−2)\),请替换\(x=−2\)。 | 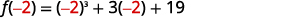 |
| 简化。 | 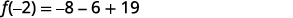 |
 |
|
| 除以时,余数\(f(x)=x^3+3x+19\)为 5\(x+2\)。 | |
| 检查: 使用合成除法进行检查。 |
|
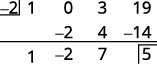 |
|
| 其余为 5。 |
当除以时,使用余数定理\(f(x)=x^3+4x+15\)求余数\(x+2\)。
- 回答
-
\(−1\)
当除以时,使用余数定理\(f(x)=x^3−7x+12\)求余数\(x+3\)。
- 回答
-
\(6\)
当我们在示例\(2a+3\)中\(8a^3+27\)除以时,结果是\(4a^2−6a+9\)。 要检查我们的工作,我们\(4a2−6a+9\)乘\(2a+3\)以得到\(8a^3+27\)。
\[(4a^2−6a+9)(2a+3)=8a^3+27 \nonumber \]
这样写,我们可以看出这一点,\(4a^2−6a+9\)\(2a+3\)也是其中的因素\(8a^3+27\)。 当我们进行除法时,余数为零。
每当除数\(x−c\)、除以多项式函数\(f(x)\)、并得出零的余数时,我们\(x−c\)都说是因子\(f(x)\)。
反之亦然。 如果\(x−c\)是因子,\(f(x)\)则\(x−c\)将除以多项式函数,得出零的余数。
我们将在因子定理中说明这一点。
对于任何多项式函数\(f(x)\),
- 如果\(x−c\)是系数\(f(x)\),那么\(f(c)=0\)
- if\(f(c)=0\),那么\(x−c\)是一个因子\(f(x)\)
使用余数定理来确定是否\(x−4\)是因子\(f(x)=x^3−64\)。
解决方案
因子定理告诉我们\(x−4\)这是\(f(x)=x^3−64\)假设的因子\(f(4)=0\)。
\(\begin{array} {ll} {} &{f(x)=x^3−64} \\[5pt] {\text{To evaluate }f(4) \text{ substitute } x=4.} &{f(4)=4^3−64} \\[5pt] {\text{Simplify.}} &{f(4)=64−64} \\[5pt]{\text{Subtract.}} &{f(4)=0} \end{array}\)
因为\(f(4)=0, x−4\)是其中一个因素\(f(x)=x^3−64\)。
使用因子定理来确定是否\(x−5\)是因子\(f(x)=x^3−125\)。
- 回答
-
是的
使用因子定理来确定是否\(x−6\)是因子\(f(x)=x^3−216\)。
- 回答
-
是的
访问这些在线资源,获取有关除法多项式的更多指导和练习。
- 将多项式除以二项式
- 合成除法和余数定理
关键概念
- 将多项式除以单项式
- 要将多项式除以单项式,请将多项式的每个项除以单项式。
- 多项式函数的除法
- 对于函数\(f(x)\)\(g(x)\),在哪里\(g(x)\neq 0\),
\(\left(\dfrac{f}{g}\right)(x)=\dfrac{f(x)}{g(x)}\)
- 对于函数\(f(x)\)\(g(x)\),在哪里\(g(x)\neq 0\),
- 余数定理
- 如果多项式函数\(f(x)\)除以\(x−c\),则余数为\(f(c)\)。
- 因子定理:对于任何多项式函数\(f(x)\),
- 如果\(x−c\)是系数\(f(x)\),那么\(f(c)=0\)
- if\(f(c)=0\),那么\(x−c\)是一个因子\(f(x)\)


