5.4: 乘以多项式
- Page ID
- 203898
在本节结束时,您将能够:
- 乘以单项式
- 将多项式乘以单项式
- 将二项式乘以二项式
- 将多项式乘以多项式
- 乘以特殊产品
- 乘以多项式函数
在开始之前,请参加这个准备测验。
乘以单项式
我们已经准备好对多项式进行运算。 由于单项式是代数表达式,因此我们可以使用指数的属性将单项式相乘。
乘以:
- \((3x^2)(−4x^3)\)
- \(\left(\frac{5}{6}x^3y\right)(12xy^2).\)
- 回答 a
-
\(\begin{array} {ll} {} &{(3x^2)(−4x^3)} \\ {\text{Use the Commutative Property to rearrange the terms.}} &{3·(−4)·x^2·x^3} \\ {\text{}} &{−12x^5} \\ \end{array} \)
- 答案 b
-
\(\begin{array} {ll} {} &{\left(\frac{5}{6}x^3y\right)(12xy^2)} \\ {\text{Use the Commutative Property to rearrange the terms.}} &{\frac{5}{6}·12·x^3·x·y·y^2} \\ {\text{Multiply.}} &{10x^4y^3} \\ \end{array} \)
乘以:
- \((5y^7)(−7y^4)\)
- \((25a^4b^3)(15ab^3)\)
- 回答 a
-
\(−35y^{11}\)
- 答案 b
-
\(375 a^5b^6\)
乘以:
- \((−6b^4)(−9b^5)\)
- \((23r^5s)(12r^6s^7).\)
- 回答 a
-
\(54b^9\)
- 答案 b
-
\(276 r^{11}s^8\)
将多项式乘以单项式
将多项式乘以单项式实际上只是应用分布属性。
乘以:
- \(−2y(4y^2+3y−5)\)
- \(3x^3y(x^2−8xy+y^2)\)。
- 回答 a
-
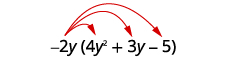
分发。 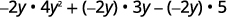
乘以。 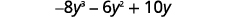
- 答案 b
-
\(\begin{array} {ll} {} &{3x^3y(x^2−8xy+y^2)} \\ {\text{Distribute.}} &{3x^3y⋅x^2+(3x^3y)⋅(−8xy)+(3x^3y)⋅y^2} \\ {\text{Multiply.}} &{3x^5y−24x^4y^2+3x^3y^3} \\ \end{array} \)
乘以:
- \(-3y(5y^2+8y^{7})\)
- \(4x^2y^2(3x^2−5xy+3y^2)\)
- 回答 a
-
\(−15y^3−24y^8\)
- 答案 b
-
\(12x^4y^2−20x^3y^3+12x^2y^4\)
乘以:
- \(4x^2(2x^2−3x+5)\)
- \(−6a^3b(3a^2−2ab+6b^2)\)
- 回答 a
-
\(8x^4−12x^3+20x^2\)
- 答案 b
-
\(−18a^5b+12a^4b^2−36a^3b^3\)
将二项式乘以二项式
就像有不同的方法来表示数字的乘法一样,有几种方法可以用来将二项式乘以二项式。 我们将首先使用分配财产。
乘以:
- \((y+5)(y+8)\)
- \((4y+3)(2y−5)\)。
- 回答
-
ⓐ
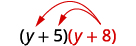
分发\((y+8)\)。 
再次分发。 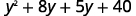
将相似的术语组合在一起。 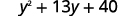
ⓑ
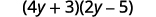
分发。 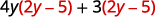
再次分发。 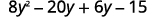
将相似的术语组合在一起。 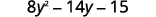
乘以:
- \((x+8)(x+9)\)
- \((3c+4)(5c−2)\)。
- 回答 a
-
\(x^2+17x+72\)
- 答案 b
-
\(15c^2+14c−8\)
乘以:
- \((5x+9)(4x+3)\)
- \((5y+2)(6y−3)\)。
- 回答 a
-
\(20x^2+51x+27\)
- 答案 b
-
\(30y^2−3y−6\)
如果你经常乘以二项式,你可能会注意到一种模式。 请注意,结果中的第一个项是每个二项式中第一个项的乘积。 第二个和第三项是两个外部项相乘的乘积,然后是两个内部项的乘积。 最后一个术语是将最后两个项相乘得出,
我们将 “第一、外部、内部、最后” 缩写为 FOIL。 字母代表 “第一、外部、内部、最后”。 我们用它作为乘以二项式的另一种方法。 FOIL 这个词很容易记住,可以确保我们找到所有四种产品。
让我们\((x+3)(x+7)\)使用这两种方法进行乘法。

我们在下面总结了 FOIL 方法的步骤。 FOIL 方法仅适用于乘以二项式,不适用于其他多项式!

当你乘以 FOIL 方法时,画出线条可以帮助你的大脑专注于图案,使其更容易使用。
现在我们将举一个例子,我们使用 FOIL 模式将两个二项式相乘。
乘以:
- \((y−7)(y+4)\)
- \((4x+3)(2x−5)\)。
- 回答
-
一个。

b。

乘以:
- \((x−7)(x+5)\)
- \((3x+7)(5x−2)\)。
- 回答
-
a.\(x^2−2x−35\)
b。\(15x^2+29x−14\)
乘以:
- \((b−3)(b+6)\)
- \((4y+5)(4y−10)\)。
- 回答
-
a.\(b^2+3b−18\)
b。\(16y^2−20y−50\)
最后一个例子中的最终乘积是三项式,因为我们可以将两个中间项结合起来。 情况并非总是如此。
乘以:
- \((n^2+4)(n−1)\)
- \((3pq+5)(6pq−11)\)。
- 回答
-
一个。
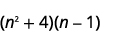
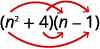
第 1 步。 将第一个项相乘。 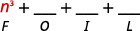
第 2 步。 将外部项相乘。 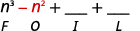
第 3 步。 将内部项相乘。 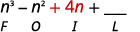
第 4 步。 将最后一个项相乘。 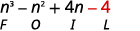
第 5 步。 用相似的术语组合起来——没有。 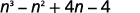
b。
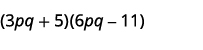
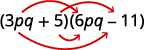
第 1 步。 将第一个项相乘。 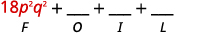
第 2 步。 将外部项相乘。 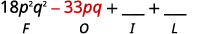
第 3 步。 将内部项相乘。 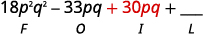
第 4 步。 将最后一个项相乘。 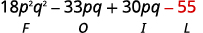
第 5 步。 将相似的术语组合在一起。 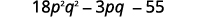
乘以:
- \((x^2+6)(x−8)\)
- \((2ab+5)(4ab−4)\)。
- 回答
-
a.\(x^3−8x^2+6x−48\)
b。\(8a^2b^2+12ab−20\)
乘以:
- \((y^2+7)(y−9)\)
- \((2xy+3)(4xy−5)\)。
- 回答
-
a.\(y^3−9y^2+7y−63\)
b。\(8x^2y^2+2xy−15\)
FOIL 方法通常是将两个二项式相乘的最快方法,但它仅适用于二项式。 您可以使用分布属性来查找任意两个多项式的乘积。 另一种适用于所有多项式的方法是垂直法。 它非常像你用来乘以整数的方法。 仔细看这个将两位数相乘的例子。

现在我们将应用同样的方法将两个二项式相乘。
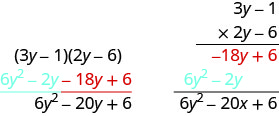
使用垂直方法乘以:\((3y−1)(2y−6)\).
- 回答
-
哪个二项式排在顶部并不重要。
\ (\ begin {align*} & &\ quad\;\; 3y-1\\ [4pt]
& &\ 下划线 {\ quad\ times\; 2y-6}\\ [4pt]
&\ text {乘以} 3y-1\ text {by} -6。 & &\ quad -18y + 6 &\ text {部分产品}\\ [4pt]
&\ text {乘以} 3y-1\ text {by} 2y。 & &\ 下划线 {6y^2-2y} &\ text {部分产品}\\ [4pt]
&\ text {添加点赞条款。} & & 6y^2-20y + 6\ end {align*}\)请注意,部分产品与 FOIL 方法中的条款相同。
使用垂直方法乘以:\((5m−7)(3m−6)\).
- 回答
-
\(15m^2−51m+42\)
使用垂直方法乘以:\((6b−5)(7b−3)\).
- 回答
-
\(42b^2−53b+15\)
我们现在使用了三种方法来乘以二项式。 一定要练习每种方法,然后尝试决定你更喜欢哪种方法。 这里列出了所有方法,以帮助您记住它们。
要乘以二项式,请使用:
- 分配财产
- 铝箔法
- 垂直法
将多项式乘以多项式
我们将单项式乘以单项式,将单项式乘以多项式,将二项式乘以二项式。 现在我们已经准备好将多项式乘以多项式了。 请记住,FOIL 在这种情况下不起作用,但我们可以使用分布属性或垂直方法。
\((b+3)(2b^2−5b+8)\)使用 ⓐ 分布属性和 ⓑ 垂直法相乘。
- 回答
-
一个。
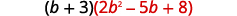
分发。 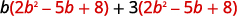
乘以。 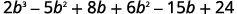
将相似的术语组合在一起。 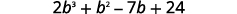
b. 将项数较少的多项式放在底部比较容易,因为这样我们得到的偏积就更少了。
\((2b^2−5b+8)\)乘以 3。
\((2b^2−5b+8)\)乘以\(b\)。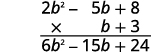
添加点赞条款。 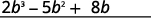
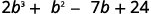
\((y−3)(y^2−5y+2)\)使用 ⓐ 分布属性和 ⓑ 垂直法相乘。
- 回答
-
a.\(y^3−8y^2+17y−6\)
b。\(y^3−8y^2+17y−6\)
\((x+4)(2x^2−3x+5)\)使用 a) 分布属性和 b) 垂直法相乘。
- 回答
-
a. 和 b。\(2x^3+5x^2−7x+20\)
我们现在已经看到了两种方法可以用来将多项式乘以多项式。 在你练习了每种方法之后,你可能会发现自己更喜欢一种方法而不是另一种方法。 为了便于参考,我们在此列出了这两种方法。
要将三项式乘以二项式,请使用:
- 分配财产
- 垂直法
乘以特殊产品
数学家喜欢寻找能使他们的工作更轻松的模式。 这方面的一个很好的例子是二项式的平方。 虽然你总是可以通过将二项式写入两次并将其相乘来获得乘积,但如果你学会使用模式,工作要做的事情就少了。 让我们先看三个例子,然后寻找一种模式。
看看这些结果。 你看到任何图案了吗?
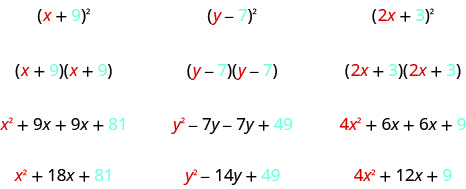
那么术语的数量呢? 在每个例子中,我们求一个二项式的平方,结果是三项式。
\[(a+b)^2=\text{___}+\text{___}+\text{___} \nonumber\]
现在看每个结果中的第一个术语。 它来自哪里?
第一个项是每个二项式的第一个项的乘积。 由于二项式是相同的,它只是第一个项的平方!
\[(a+b)^2=a^2+\text{___}+\text{___} \nonumber\]
要获得乘积的第一个项,请对第一个项进行平方。
最后一个学期来自哪里? 看看例子并找到模式。
最后一个项是最后一个项的乘积,即最后一个项的平方。
\[(a+b)^2=\text{___}+\text{___}+b^2 \nonumber\]
要获得产品的最后一个项,请将最后一个项相乘。
最后,看看中间学期。 请注意,它源于添加 “外部” 和 “内部” 术语——两者都是一样的! 因此,中间项是二项式两个项乘积的两倍。
\[(a+b)^2=\text{___}+2ab+\text{___} \nonumber\]
\[(a−b)^2=\text{___}−2ab+\text{___} \nonumber\]
要得出产品的中间项,请将这些项相乘并将其乘积加倍。
把它们放在一起:
如果 a 和 b 是实数,

要对二项式求平方,请将第一个项求平方,将最后一个项乘积加倍。
乘以:a.\((x+5)^2\) b\((2x−3y)^2\).
- 回答
-
一个。
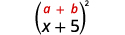
用第一个术语求平方。 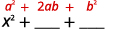
用最后一个术语求平方。 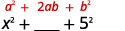
将他们的产品加倍。 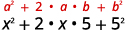
简化。 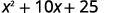
b。
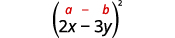
使用图案。 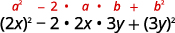
简化。 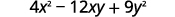
乘以:a.\((x+9)^2\) b\((2c−d)^2\).
- 回答
-
a.\(x^2+18x+81\)
b。\(4c^2−4cd+d^2\)
乘以:a.\((y+11)^2\) b\((4x−5y)^2\).
- 回答
-
a.\(y^2+22y+121\)
b。\(16x^2−40xy+25y^2\)
我们刚刚看到了一种二项式求平方的模式,我们可以用它来简化一些二项式的乘法。 同样,二项式的另一种乘积也有一种模式。 但是在我们开始之前,我们需要介绍一些词汇。
一对二项式的第一个项和最后一个项相同,但一个是总和,一个是差值,被称为共轭对\((a−b)\),其形式为\((a+b)\)。
共轭对是两个形式的二项式
\[(a−b), (a+b). \nonumber\]
两对二项式的第一个项和最后一个项相同,但是一个二项式是总和,另一个是差异。
找到共轭物的乘积有很好的模式。 当然,你可以简单地用 FOIL 来获得产品,但是使用这种模式可以让你的工作更轻松。 让我们使用 FOIL 乘以一些共轭对来寻找模式。
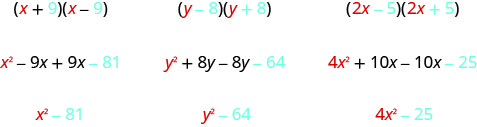
您对这些产品有什么看法?
两个二项式的乘积也是二项式! 由FOIL产生的大多数产品都是三项式的。
每个第一个项都是二项式第一个项的乘积,由于它们是相同的,因此它是第一个项的平方。
\[(a+b)(a−b)=a^2−\text{___} \nonumber\]
要获得第一个项,请将第一个项求平方。
最后一个术语来自于最后一个项的乘积,即最后一个学期的平方。
\[(a+b)(a−b)=a^2−b^2 \nonumber\]
要获得最后一个学期,请将最后一个学期相乘。
为什么没有中间学期? 请注意,在每种情况下,你从 FOIL 中得到的两个中间项组合为 0,这是一加一减的结果。
共轭物的乘积总是这样的\(a^2−b^2\)。 这称为平方差。
这导致了以下模式:
如果 a 和 b 是实数,

该乘积称为平方差。
要乘以共轭,请将第一个项求平方,将最后一个项写成平方差。
使用共轭物图案乘以:a.\((2x+5)(2x−5)\) b\((5m−9n)(5m+9n)\).
- 回答
-
一个。
二项式是共轭物吗? 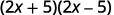
它是偶联物的产物。 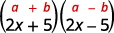
将第一个项平方,2x.2x。 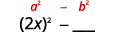
最后一个学期的平方,5.5。 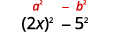
简化。 该乘积是平方差。 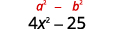
b。
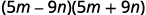
这符合图案。 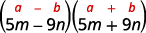
使用图案。 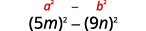
简化。 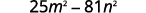
乘以:a.\((6x+5)(6x−5)\) b\((4p−7q)(4p+7q)\).
- 回答
-
a.\(36x^2−25\)
b。\(16p^2−49q^2\)
乘以:a.\((2x+7)(2x−7)\) b\((3x−y)(3x+y)\).
- 回答
-
a.\(4x^2−49\) b。\(9x^2−y^2\)
我们刚刚为二项式方块和共轭物乘积开发了特殊的乘积模式。 这些产品看起来很相似,因此重要的是要识别何时适合使用每种模式,并注意它们的不同之处。 一起看这两种模式,注意它们的相似之处和不同之处。
| 二项式方块 | 共轭物的乘积 |
|---|---|
| \((a+b)^2=a^2+2ab+b^2\) | \((a−b)(a+b)=a^2−b^2\) |
| \((a−b)^2=a^2−2ab+b^2\) | |
| • 求二项式的平方 | • 乘以共轭物 |
| • 产品是三项式 | • 产品是二项式。 |
| • FOIL 的内部和外部术语是相同的。 | • FOIL 的内在术语和外部术语是相反的。 |
| • 中间术语是术语乘积的两倍 | • 没有中间术语。 |
选择合适的图案并使用它来查找产品:
a.\((2x−3)(2x+3)\) b.\((8x-5)^2\) c.\((6m+7)^2\) d\((5x−6)(6x+5)\).
- 回答
-
一个。\((2x−3)(2x+3)\)
这些是共轭物。 它们具有相同的第一个数字和相同的最后一个数字,一个二项式是总和,另一个是差值。 它符合共轭物乘积模式。
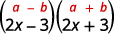
使用图案。 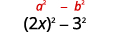
简化。 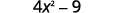
b。\((8x−5)^2\)
我们被要求对二项式求平方。 它符合二项式方块图案。
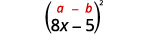
使用图案。 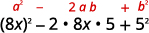
简化。 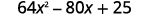
c。\((6m+7)^2\)
同样,我们将对二项式进行平方,因此我们使用二项式方块图案。
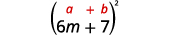
使用图案。 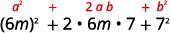
简化。 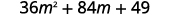
d。\((5x−6)(6x+5)\)
本产品不符合图案,因此我们将使用 FOIL。
\(\begin{array} {ll} {} &{(5x−6)(6x+5)} \\ {\text{Use FOIL.}} & {30x^2+25x−36x−30} \\ {\text{Simplify.}} & {30x^2−11x−30} \\ \end{array}\)
选择合适的图案并使用它来查找产品:
a.\((9b−2)(2b+9)\) b.\((9p−4)^2\) c.\((7y+1)^2\) d\((4r−3)(4r+3)\).
- 回答
-
a. FOIL;\(18b^2+77b−18\)
b. 二项式方块;\(81p^2−72p+16\)
c. 二项式方块;\(49y^2+14y+1\)
d. 共轭物的乘积;\(16r^2−9\)
选择合适的图案并使用它来查找产品:
a.\((6x+7)^2\) b.\((3x−4)(3x+4)\) c.\((2x−5)(5x−2)\) d\((6n−1)^2\).
- 回答
-
a. 二项式方块;\(36x^2+84x+49\)b. 共轭物的乘积;\(9x^2−16\)c. FOIL;\(10x^2−29x+10\)d. 二项式方块;\(36n^2−12n+1\)
乘以多项式函数
就像可以乘以多项式一样,多项式函数也可以相乘。
对于函数\(f(x)\)和\(g(x)\),
\[(f·g)(x)=f(x)·g(x)\]
对于函数\(f(x)=x+2\)和\(g(x)=x^2−3x−4\),请查找:
- \((f·g)(x)\)
- \((f·g)(2)\)。
- 回答
-
一个。
\(\begin{array} {ll} {} &{(f·g)(x)=f(x)·g(x)} \\ {\text{Substitute for } f(x) \text{ and } g(x)} &{(f·g)(x)=(x+2)(x^2−3x−4)} \\ {\text{Multiply the polynomials.}} &{(f·g)(x)=x(x^2−3x−4)+2(x^2−3x−4)} \\ {\text{Distribute.}} &{(f·g)(x)=x3−3x^2−4x+2x^2−6x−8} \\ {\text{Combine like terms.}} &{(f·g)(x)=x3−x^2−10x−8} \\ \end{array}\)
b. 在 a 部分中,我们找到了\((f·g)(x)\),现在被要求去找\((f·g)(2)\)。
\(\begin{array} {ll} {} &{(f·g)(x)=x^3−x^2−10x−8} \\ {\text{To find }(f·g)(2), \text{ substitute } x=2.} &{(f·g)(2)=2^3−2^2−10·2−8} \\ {} &{(f·g)(2)=8−4−20−8} \\ {} &{(f·g)(2)=−24} \\ \end{array}\)
对于函数\(f(x)=x−5\)和\(g(x)=x^2−2x+3\),请查找
- \((f·g)(x)\)
- \((f·g)(2)\)。
- 回答 a
-
\((f·g)(x)=x^3−7x^2+13x−15\)
- 答案 b
-
\((f·g)(2)=−9\)
对于函数\(f(x)=x−7\)和\(g(x)=x^2+8x+4\),请查找
- \((f·g)(x)\)
- \((f·g)(2)\)。
- 回答 a
-
\((f·g)(x)=x^3+x^2−52x−28\)
- 回答 a
-
\((f·g)(2)=−120\)
访问此在线资源以获取更多指导和练习乘法多项式。
- 二项式特殊产品简介
关键概念
- 如何使用 FOIL 方法乘以两个二项式。
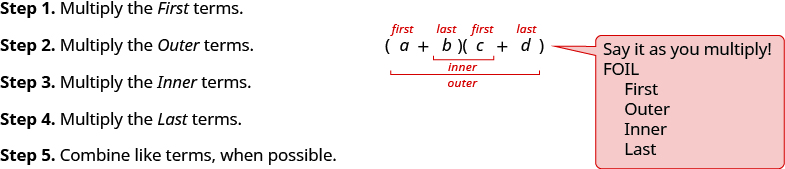
- 将两个二项式相乘:要乘以二项式,请使用:
- 分配财产
- 铝箔法
- 将@@ 多项式乘以多项式:要将三项式乘以二项式,请使用:
- 分配财产
- 垂直法
- 二项式正方形图案
如果 a 和 b 是实数,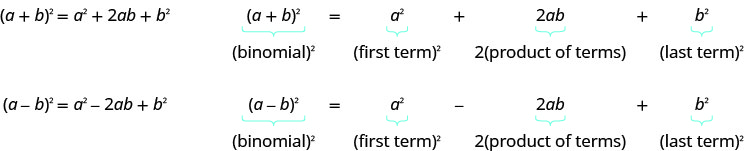
- 共轭物模式的乘积
如果 a, b 是实数
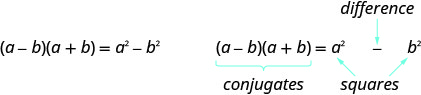
乘积称为平方差。
要乘以共轭,请将第一个项求平方,将最后一个项写成平方差。 - 比较特殊的产品模式
二项式方块 共轭物的乘积 \((a+b)^2=a^2+2ab+b^2\) \((a−b)^2=a^2−2ab+b^2\) \((a−b)(a+b)=a^2−b^2\) • 求二项式的平方 • 乘以共轭物 • 产品是三项式 • 产品是二项式。 • FOIL 的内部和外部术语是相同的。 • FOIL 的内在术语和外部术语是相反的。 • 中间术语是术语乘积的两倍 • 没有中间术语。 - 多项式函数的乘法:
- 对于函数\(f(x)\)和\(g(x)\),
\[(f⋅g)(x)=f(x)⋅g(x) \nonumber\]
- 对于函数\(f(x)\)和\(g(x)\),
词汇表
- 共轭对
- 共轭对是两个形式为\((a−b)\)和的二项式\((a+b)\)。 两对二项式的第一个项和最后一个项相同,但是一个二项式是总和,另一个是差异。


