5.2E：练习

练习成就完美

确定多项式的类型

在以下练习中，确定多项式是单项式、二项式、三项式还是其他多项式。 还要给出每个多项式的次数。

1. ⓐ\(47x^5−17x^2y^3+y^2\)
ⓑ\(5c^3+11c^2−c−8\)
ⓒ\(59ab+13b\)
ⓓ\(4\)
ⓔ\(4pq+17\)

回答

ⓐ 三项式，度 5
ⓑ 其他多项式，度 3
ⓒ 二项式，度 2
ⓓ 单项式，度 0
ⓔ 二项式，度 2

2. ⓐ\(x^2−y^2\)
ⓑ\(−13c^4\)
ⓒ\(a^2+2ab−7b^2\)
ⓓ\(4x^2y^2−3xy+8\)
ⓔ\(19\)

3. ⓐ\(8y−5x\)
ⓑ\(y^2−5yz−6z^2\)
ⓒ\(y^3−8y^2+2y−16\)
ⓓ\(81ab^4−24a^2b^2+3b\)
ⓔ\(−18\)

回答

ⓐ 二项式、度 1
ⓑ 三项式、度 2
ⓒ 其他多项式、度 3
ⓓ 三项式、度 5
ⓔ 单项式、度 0

4. ⓐ\(11y^2\)
ⓑ\(−73\)
ⓒ\(6x^2−3xy+4x−2y+y^2\)
ⓓ\(4y^2+17z^2\)
ⓔ\(5c^3+11c^2−c−8\)

5. ⓐ\(5a^2+12ab−7b^2\)
ⓑ\(18xy^2z\)
ⓒ\(5x+2\)
ⓓ\(y^3−8y^2+2y−16\)
ⓔ\(−24\)

回答

ⓐ 三项式、度 2
ⓑ 单项式、度 4
ⓒ 二项式、度 1
ⓓ 其他多项式、度 3
ⓔ 单项式、度 0

6. ⓐ\(9y^3−10y^2+2y−6\)
ⓑ\(−12p^3q\)
ⓒ\(a^2+9ab+18b^2\)
ⓓ\(20x^2y^2−10a^2b^2+30\)
ⓔ\(17\)

7. ⓐ\(14s−29t\)
ⓑ\(z^2−5z−6\)
ⓒ\(y^3−8y^2z+2yz^2−16z^3\)
ⓓ\(23ab^2−14\)
ⓔ\(−3\)

回答

ⓐ 二项式，度 1
ⓑ 三项式，度 2
ⓒ 其他多项式，度 3
ⓓ 二项式，度 3
ⓔ 单项式，度 0

8. ⓐ\(15xy\)
ⓑ\(15\)
ⓒ\(6x^2−3xy+4x−2y+y^2\)
ⓓ\(10p−9q\)
ⓔ\(m^4+4m^3+6m^2+4m+1\)

加减多项式

在以下练习中，添加或减去单项式。

9. ⓐ\(7x^2+5x^2\)
ⓑ\(4a−9a\)

回答

ⓐ\(12x^2\) ⓑ\(−5a\)

10. ⓐ\(4y^3+6y^3\)
ⓑ\(−y−5y\)

11. ⓐ\(−12w+18w\)
ⓑ\(7x^2y−(−12x^2y)\)

回答

ⓐ\(6w\)
ⓑ\(19x^2y\)

12. ⓐ\(−3m+9m\)
ⓑ\(15yz^2−(−8yz^2)\)

13。 \(7x^2+5x^2+4a−9a\)

回答

\(12x^2−5a\)

14。 \(4y^3+6y^3−y−5y\)

15。 \(−12w+18w+7x^2y−(−12x^2y)\)

回答

\(6w+19x^2y\)

16。 \(−3m+9m+15yz^2−(−8yz^2)\)

17. ⓐ\(−5b−17b\)
ⓑ\(3xy−(−8xy)+5xy\)

回答

ⓐ\(−22b\)
ⓑ\(16xy\)

18. ⓐ\(−10x−35x\)
ⓑ\(17mn^2−(−9mn^2)+3mn^2\)

19. ⓐ\(12a+5b−22a\)
ⓑ\(pq^2−4p−3q^2\)

回答

ⓐ\(−10a+5b\)
ⓑ\(pq^2−4p−3q^2\)

20. ⓐ\(14x−3y−13x\)
ⓑ\(a^2b−4a−5ab^2\)

21. ⓐ\(2a^2+b^2−6a^2\)
ⓑ\(x^2y−3x+7xy^2\)

回答

ⓐ\(−4a^2+b^2\)
ⓑ\(x^2y−3x+7xy^2\)

22. ⓐ\(5u^2+4v^2−6u^2\)
ⓑ\(12a+8b\)

23. ⓐ\(xy^2−5x−5y^2\)
ⓑ\(19y+5z\)

回答

ⓐ\(xy^2−5x−5y^2\)
ⓑ\(19y+5z\)

24。 \(12a+5b−22a+pq^2−4p−3q^2\)

25。 \(14x−3y−13x+a^2b−4a−5ab^2\)

回答

\(x−3y+a^2b−4a−5ab^2\)

26。 \(2a^2+b^2−6a^2+x^2y−3x+7xy^2\)

27。 \(5u^2+4v^2−6u^2+12a+8b\)

回答

\(−u^2+4v^2+12a+8b\)

28。 \(xy^2−5x−5y^2+19y+5z\)

29。 添加：\(4a,−3b,−8a\)

回答

\(−4a−3b\)

30。 添加：\(4x,3y,−3x\)

31。 \(5x^6\)从中减去\(−12x^6\)

回答

\(−7x^6\)

32。 \(2p^4\)从中减去\(−7p^4\)

在以下练习中，添加多项式。

33。 \((5y^2+12y+4)+(6y^2−8y+7)\)

回答

\(11y^2+4y+11\)

34。 \((4y^2+10y+3)+(8y^2−6y+5)\)

35。 \((x^2+6x+8)+(−4x^2+11x−9)\)

回答

\(−3x^2+17x−1\)

36。 \((y^2+9y+4)+(−2y^2−5y−1)\)

37。 \((8x^2−5x+2)+(3x^2+3)\)

回答

\(11x^2−5x+5\)

38。 \((7x^2−9x+2)+(6x^2−4)\)

39。 \((5a^2+8)+(a^2−4a−9)\)

回答

\(6a^2−4a−1\)

40。 \((p^2−6p−18)+(2p^2+11)\)

在以下练习中，减去多项式。

41。 \((4m^2−6m−3)−(2m^2+m−7)\)

回答

\(2m^2−7m+4\)

42。 \((3b^2−4b+1)−(5b^2−b−2)\)

43。 \((a^2+8a+5)−(a^2−3a+2)\)

回答

\(11a+3\)

44。 \((b^2−7b+5)−(b^2−2b+9)\)

45。 \((12s^2−15s)−(s−9)\)

回答

\(12s^2−14s+9\)

46。 \((10r^2−20r)−(r−8)\)

在以下练习中，减去多项式。

47。 \((9x^2+2)\)从中减去\((12x^2−x+6)\)

回答

\(3x^2−x+4\)

48。 \((5y^2−y+12)\)从中减去\((10y^2−8y−20)\)

49。 \((7w^2−4w+2)\)从中减去\((8w^2−w+6)\)

回答

\(w^2+3w+4\)

50。 \((5x^2−x+12)\)从中减去\((9x^2−6x−20)\)

在以下练习中，找出多项式的差异。

51。 找出\((w^2+w−42)\)和的区别\((w^2−10w+24)\)

回答

\(11w−64\)

52。 找出\((z^2−3z−18)\)和的区别\((z^2+5z−20)\)

在以下练习中，添加多项式。

53。 \((7x^2−2xy+6y^2)+(3x^2−5xy)\)

回答

\(10x^2−7xy+6y^2\)

54。 \((−5x^2−4xy−3y^2)+(2x^2−7xy)\)

55。 \((7m^2+mn−8n^2)+(3m^2+2mn)\)

回答

\(10m^2+3mn−8n^2\)

56。 \((2r^2−3rs−2s^2)+(5r^2−3rs)\)

在以下练习中，将多项式相加或减去。

57。 \((a^2−b^2)−(a^2+3ab−4b^2)\)

回答

\(−3ab+3b^2\)

58。 \((m^2+2n^2)−(m^2−8mn−n^2)\)

59。 \((p^3−3p^2q)+(2pq^2+4q^3)−(3p^2q+pq^2)\)

回答

\(p^3−6p^2q+pq^2+4q^3\)

60。 \((a^3−2a^2b)+(ab^2+b^3)−(3a^2b+4ab^2)\)

61。 \((x^3−x^2y)−(4xy^2−y^3)+(3x^2y−xy^2)\)

回答

\(x^3+2x^2y−5xy^2+y^3\)

62。 \((x^3−2x^2y)−(xy^2−3y^3)−(x^2y−4xy^2)\)

计算给定值的多项式函数

在以下练习中，找到每个多项式函数的函数值。

63。 对于该函数\(f(x)=8x^2−3x+2\)，请查找：
ⓐ\(f(5)\) ⓑ\(f(−2)\) ⓒ\(f(0)\)

回答

ⓐ\(187\) ⓑ\(40\) ⓒ\(2\)

64。 对于该函数\(f(x)=5x^2−x−7\)，请查找：
ⓐ\(f(−4)\) ⓑ\(f(1)\) ⓒ\(f(0)\)

65。 对于该函数\(g(x)=4−36x\)，请查找：
ⓐ\(g(3)\) ⓑ\(g(0)\) ⓒ\(g(−1)\)

回答

ⓐ\(−104\) ⓑ\(4\) ⓒ\(40\)

66。 对于该函数\(g(x)=16−36x^2\)，请查找：
ⓐ\(g(−1)\) ⓑ\(g(0)\) ⓒ\(g(2)\)

在以下练习中，找出每个多项式函数的高度。

67。 一位画家从一\(75\)英尺高的平台上掉下画笔。 多项式函数\(h(t)=−16t^2+75\)给出画笔掉落\(t\)几秒后的高度。 在\(t=2\)几秒钟后找到高度。

回答

高度为 11 英尺。

68。 一个女孩把球从悬崖上丢到海里。 多项式\(h(t)=−16t^2+200\)给出了球掉落\(t\)几秒钟后的高度。 在\(t=3\)几秒钟后找到高度。

69。 一家立体声扬声器制造商发现，以每台扬声器的成本出售扬声器所获得的\(p\)收入由多项式函数给出\(R(p)=−4p^2+420p\)。 找出以\(p=60\)美元计时获得的收入。

回答

收入为10,800美元。

70。 一家最新篮球鞋的制造商发现，以每双\(p\)美元的成本出售篮球鞋所获得的收入由多项式给出\(R(p)=−4p^2+420p\)。 找出以\(p=90\)美元计时获得的收入。

71。 多项式\(C(x)=6x^2+90x\)给出了生产矩形容器的成本（以美元为单位），该容器的顶部和底部是正方形，侧\(x\)脚和高度\(6\)英尺。 找出生产带\(x=4\)脚的盒子的成本。

回答

费用为456美元。

72。 多项式\(C(x)=6x^2+90x\)给出了生产矩形容器的成本（以美元为单位），该容器的顶部和底部是正方形，侧\(x\)脚和高度\(4\)英尺。 找出生产带\(x=6\)脚的盒子的成本。

加减多项式函数

在每个示例中，找到 ⓐ\((f+g)(x)\) ⓑ\((f+g)(2)\) ⓒ\((f-g)(x)\) ⓓ\((f-g)(3)\)。

73。 \(f(x)=2x^2−4x+1\)和\(g(x)=5x^2+8x+3\)

回答

ⓐ\((f+g)(x)=7x^2+4x+4\)
ⓑ\((f+g)(2)=40\)
ⓒ\((f−g)(x)=−3x^2−12x−2\)
ⓓ\((f−g)(−3)=7\)

74。 \(f(x)=4x^2−7x+3\)和\(g(x)=4x^2+2x−1\)

75。 \(f(x)=3x^3−x^2−2x+3\)和\(g(x)=3x^3−7x\)

回答

ⓐ\((f+g)(x)=6x^3−x^2−9x+3\)
ⓑ\((f+g)(2)=29\)
ⓒ\((f−g)(x)=−x^2+5x+3\)
ⓓ\((f−g)(−3)=−21\)

76。 \(f(x)=5x^3−x^2+3x+4\)和\(g(x)=8x^3−1\)

写作练习

77。 用你自己的话来解释单项式、二项式和三项式之间的区别。

回答

答案会有所不同。

78。 用你自己的话解释具有五个项的多项式和度数为的多项式之间的区别\(5\)。

79。 阿丽亚娜认为总和\(6y^2+5y^4\)是\(11y^6\)。 她的推理有什么问题？

回答

答案会有所不同。

80。 每个三项式都是二次多项式吗？ 如果不是，请举个例子。

自检

ⓐ 完成练习后，使用这份清单来评估你对本节目标的掌握程度。

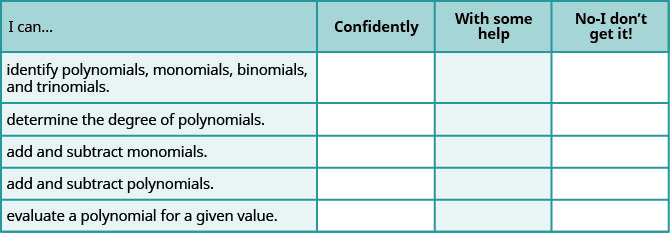
ⓑ 如果你的大部分支票是：

... 自信地。 恭喜！ 您已经实现了本节中的目标。 反思一下你使用的学习技能，这样你就可以继续使用它们。 为了确信自己有能力做这些事情，你做了什么？ 具体一点。

... 在一些帮助下。 必须迅速解决这个问题，因为你不掌握的话题会成为你通往成功之路的坑洼。 在数学中，每个主题都建立在以前的工作基础上。 在继续前进之前，请务必确保自己有坚实的基础。 你能向谁寻求帮助？ 你的同学和老师都是很好的资源。 校园里有没有可以提供数学导师的地方？ 你的学习技能可以提高吗？

... 不-我不明白！ 这是一个警告信号，你一定不能忽视它。 你应该立即得到帮助，否则你很快就会不知所措。 尽快与您的教师见面，讨论您的情况。 你可以一起制定一个计划，为你提供所需的帮助。