5.2: 加减多项式

学习目标

在本节结束时，您将能够：

• 确定多项式的次数
• 加减多项式
• 计算给定值的多项式函数
• 加减多项式函数

注意

在开始之前，请参加这个准备测验。

1. 简化：\(3x^2+3x+1+8x^2+5x+5.\)
   如果你错过了这个问题，请查看 [链接]。
2. 减去：\((5n+8)−(2n−1).\)
   如果你错过了这个问题，请查看 [链接]。
3. 评估：\(4xy^2\)何时\(x=−2x\)和\(y=5.\)。
   如果你错过了这个问题，请查看 [链接]。

确定多项式的次数

我们已经了解到，一个项是一个常量或一个常数与一个或多个变量的乘积。 单项式是具有一个项的代数表达式。 当它的形式为\(ax^m\)，其中\(a\)是常量并且\(m\)是整数时，它被称为一个变量中的单项式。 一个变量中单项式的一些例子是。 单项式也可以有多个变量，例如和\(−4a^2b^3c^2.\)

定义：单项式

单项式是具有一个项的代数表达式。 一个变量中的单项式是这种形式的项\(ax^m\)，其中\(a\)是常数，\(m\)是整数。

单项式或通过加法或减法组合的两个或多个单项式是多项式。 有些多项式根据项数有特殊的名称。 单项式是只有一个项的多项式。 二项式正好有两个项，而一个三项式正好有三个项。 超过三个项的多项式没有特殊名称。

定义：多项式

• 多项式 —由加法或减法组合的单项式或两个或多个代数项是多项式。
• 单项式 —只有一个项的多项式称为单项式。
• 二项式 —正好有两个项的多项式称为二项式。
• 三项式 —正好有三个项的多项式称为三项式。

以下是多项式的一些示例。

多项式	\(y+1\)	\(4a^2−7ab+2b^2\)	\(4x^4+x^3+8x^2−9x+1\)
单项式	\(14\)	\(8y^2\)	\(−9x^3y^5\)	\(−13a^3b^2c\)
二项式	\(a+7ba+7b\)	\(4x^2−y^2\)	\(y^2−16\)	\(3p^3q−9p^2q\)
三项式	\(x^2−7x+12\)	\(9m^2+2mn−8n^2\)	\(6k^4−k^3+8k\)	\(z^4+3z^2−1\)

请注意，每个单项式、二项式和三项式也是多项式。 它们只是多项式 “家族” 中的特殊成员，因此它们有特殊的名字。 我们在提及这些特殊多项式时使用单项式、二项式和三项式这两个词，然后将其余所有多项式称为即可。

多项式的次数及其项的次数由变量的指数决定。 没有变量，只有常量的单项式是一种特例。 常数的度数为 0。

定义：多项式的次数

• 项的度数是其变量的指数之和。
• 常数的度数为 0。
• 多项式的次数是其所有项的最高度。

让我们通过看几个多项式来看看它是如何工作的。 我们将逐步进行，从单项式开始，然后发展到具有更多项的多项式。 让我们从单项式开始。 单项式\(8ab^2\)有两个变量\(a\)和\(b\)。 要找到度数，我们需要找到指数的总和。 变量 a 没有写入指数，但请记住，这意味着指数为 1。 的指数\(b\)为 2。 指数之和 1+2,1+2 为 3，因此度数为 3。

以下是一些其他示例。

当您按度数降序列出项时，处理多项式会更容易。 当以这种方式书写多项式时，据说它是多项式的标准形式。 养成先写最高学位的学期的习惯。

示例\(\PageIndex{1}\)

确定每个多项式是单项式、二项式、三项式还是其他多项式。 然后，找到每个多项式的次数。

1. \(7y2−5y+3\)
2. \(−2a^4b^2\)
3. \(3x5−4x3−6x2+x−8\)
4. \(2y−8xy^3\)
5. \(15\)

回答

	多项式	术语数量	键入	学位学位	多项式度
ⓐ	\(7y^2−5y+3\)	3	三项式	2、1、0	2
ⓑ	\(−2a^4b^2−2a^4b^2\)	1	单项式	4、2	6
ⓒ	\(3x5−4x3−6x2+x−8\)	5	多项式	5、3、2、1、0	5
ⓓ	\(2y−8xy^3\)	2	二项式	1、4	4
ⓔ	\(15\)	1	单项式	0	0

示例\(\PageIndex{2}\)

确定每个多项式是单项式、二项式、三项式还是其他多项式。 然后，找到每个多项式的次数。

1. \(−5\)
2. \(8y^3−7y^2−y−3\)
3. \(−3x^2y−5xy+9xy^3\)
4. \(81m^2−4n^2\)
5. \(−3x^6y^3z\)

回答 a

单项式，0

答案 b

多项式，3

答案 c

三项式，3

回答 d

二项式，2

答案 b

单项式，10

示例\(\PageIndex{3}\)

确定每个多项式是单项式、二项式、三项式还是其他多项式。 然后，找到每个多项式的次数。

1. \(64k^3−8\)
2. \(9m^3+4m^2−2\)
3. \(56\)
4. \(8a^4−7a^3b−6a^2b^2−4ab^3+7b^4\)
5. \(-p^4q^3\)

回答

ⓐ 二项式，3 ⓑ 三项式，3 ⓒ 单项式，0 ⓓ 多项式，4 ⓔ 单项式，7

加减多项式

我们已经学会了如何通过组合相似的术语来简化表达式。 请记住，类似项必须具有相同的变量和相同的指数。 由于单项式是术语，因此加减单项式与合并相似项相同。 如果单项式与项类似，我们只需将它们相加或减去系数即可。

示例\(\PageIndex{4}\)

加上或减去：

1. \(25y^2+15y^2\)
2. \(16pq^3−(−7pq^3)\)。

回答 a

\( \begin{array} {ll} {} &{25y^2+15y^2} \\ {\text{Combine like terms.}} &{40y^2} \\ \end{array} \nonumber \)

答案 b

\( \begin{array} {ll} {} &{16pq^3−(−7pq^3)} \\ {\text{Combine like terms.}} &{23pq^3} \\ \end{array} \nonumber \)

示例\(\PageIndex{5}\)

加上或减去：

1. \(12q^2+9q^2\)
2. \(8mn^3−(−5mn^3)\)。

回答

ⓐ\(21q^2\) ⓑ\(13mn^3\)

示例\(\PageIndex{6}\)

加上或减去：

1. \(−15c^2+8c^2\)
2. \(−15y^2z^3−(−5y^2z^3)\)

回答

ⓐ\(−7c^2\) ⓑ\(−10y^2z^3\)

请记住，相似项必须具有相同的变量和相同的指数。

示例\(\PageIndex{7}\)

简化：

1. \(a^2+7b^2−6a^2\)
2. \(u^2v+5u^2−3v^2\)

回答

ⓐ 将相似的术语组合在一起。

\(a^2+7b^2−6a^2 \;=\; −5a^2+7b^2\)

ⓑ 没有相似的术语可以合并。 在这种情况下，多项式保持不变。

\(u^2v+5u^2−3v^2\)

示例\(\PageIndex{8}\)

添加：

1. \(8y^2+3z^2−3y^2\)
2. \(m^2n^2−8m^2+4n^2\)

回答

ⓐ\(5y^2+3z^2\)
ⓑ\(m^2n^2−8m^2+4n^2\)

示例\(\PageIndex{9}\)

添加：

1. \(3m^2+n^2−7m^2\)
2. \(pq^2−6p−5q^2\)

回答

ⓐ\(−4m^2+n^2\)
ⓑ\(pq^2−6p−5q^2\)

我们可以将加减多项式看作是将一系列单项式相加和减去。 寻找相似的术语——那些具有相同变量和相同指数的术语。 Commutative Property 允许我们重新排列条款，将相似的术语组合在一起。

示例\(\PageIndex{10}\)

找到总和:\((7y^2−2y+9)\;+\;(4y^2−8y−7)\).

回答

\ (\ begin {align*} &\ text {识别相似的术语。} & & (\ 下划线 {\ 下划线 {7y^2}} −\ 下划线 {2y} +9) + (\ 下划线 {\ 下划线 {4y^2}} −\ 下划线 {8y} −7)\\ [6pt]
&\ text {不用括号重写，}\\
&\ text {重新排列以将相似的术语组合在一起。} & &\ 下划线 {\ 下划线 {7y^2+4y^2}} −\ 下划线 {2y−8y} +9−7\\ [6pt]
&\ text {像术语一样合并。} & & 11y^2−10y+2\ end {align*}\)

示例\(\PageIndex{11}\)

找到总和：\( (7x^2−4x+5)\;+\;(x^2−7x+3)\)

回答

\(8x^2−11x+8\)

示例\(\PageIndex{12}\)

找到总和：\((14y^2+6y−4)\;+\;(3y^2+8y+5)\)

回答

\(17y^2+14y+1\)

在下一个示例中减去多项式时，在分布时要小心使用符号。

示例\(\PageIndex{13}\)

找出区别：\((9w^2−7w+5)\;−\;(2w^2−4)\)

回答

\ (\ begin {align*} & & (9w^2−7w+5)\; −\; (2w^2−4)\\ [6pt]
&\ text {分发和识别相似的术语。} & &\ 下划线 {\ 下划线 {9w^2}} −\ 下划线 {7w} +5-\ 下划线 {\ 下划线 {2w^2}} +4\\ [6pt]
&\ text {重新排列条款。} & &\ 下划线 {\ 下划线 {9w^2-2w^2}} −\ 下划线 {7w} +5+4\\ [6pt]
&\ text {合并相似的术语。} & & 7w^2−7w+9\ end {align*}\)

示例\(\PageIndex{14}\)

找出区别：\((8x^2+3x−19)\;−\;(7x^2−14)\)

回答

\(x^2+3x−5\)

示例\(\PageIndex{15}\)

找出区别：\((9b^2−5b−4)\;−\;(3b^2−5b−7)\)

回答

\(6b^2+3\)

示例\(\PageIndex{16}\)

\((p^2+10pq−2q^2)\)从... 中减去\((p^2+q^2)\)。

回答

\ (\ begin {align*} & & & (p^2+q^2)\; −\; (p^2+10pq−2q^2)\\ [6pt]
&\ text {分发和识别类似的术语。} & &\ 下划线 {\ 下划线 {p^2}} +\ 下划线 {q^2}-\ 下划线 {\ 下划线 {p^2}} -10pq +\ 下划线 {2q^2}\\ [6pt]
&\ text {重新排列术语，将相似的术语放在一起。} & &\ 下划线 {\ 下划线 {p^2-p^2}} −10pq +\ 下划线 {q^2 + 2q^2}\\ [6pt]
&\ text {像术语一样合并。} & & −10pq+3q^2\ end {align*}\)

示例\(\PageIndex{17}\)

\((a^2+5ab−6b^2)\)从中减去\((a^2+b^2)\)

回答

\(−5ab+7b^2\)

示例\(\PageIndex{18}\)

\((m^2−7mn−3n^2)\)从... 中减去\((m^2+n^2)\)。

回答

7mn+4n^2

示例\(\PageIndex{19}\)

找到总和：\((u^2−6uv+5v^2)\;+\;(3u^2+2uv)\)

回答

\ (\ begin {align*} & & & (u^2−6uv+5v^2)\; +\; (3u^2+2uv)\\ [6pt]
&\ text {分发和识别相似的术语。} & &\ 下划线 {\ 下划线 {u^2}}-\ 下划线 {6uv} +5v^2+\ 下划线 {\ 下划线 {3u^2}} +\ 下划线 {2uv}\\ [6pt]
&\ text {重新排列术语以将相似的术语组合在一起。} & &\ 下划线 {\ 下划线 {u^2}} +\ 下划线 {\ 下划线 {3u^2}}-\ 下划线 {6uv} +\ 下划线 {2uv} +5v^2\\ [6pt]
&\ text {像术语一样合并。} & & 4u^2−4uv+5v^2\ end {align*}\)

示例\(\PageIndex{20}\)

找到总和：\((3x^2−4xy+5y^2)\;+\;(2x^2−xy)\)

回答

\(5x^2−5xy+5y^2\)

示例\(\PageIndex{21}\)

找到总和：\((2x^2−3xy−2y^2)\;+\;(5x^2−3xy)\)

回答

\(7x^2−6xy−2y^2\)

当我们加上和减去两个以上的多项式时，过程是相同的。

示例\(\PageIndex{22}\)

简化：\((a^3−a^2b)\;−\;(ab^2+b^3)\;+\;(a^2b+ab^2)\)

回答

\ (\ begin {align*} & & (a^3−a^2b)\; −\; (ab^2+b^3)\; +\; (a^2b+ab^2)\\ [6pt]
&\ text {分发} & a^3−a^2-b^3 + a^2b+ab^2\\ [6pt]
&\ text {重新排列术语以将相似的术语组合在一起。} & & a^3−a^2b + a^2b− ab^2 + ab^2-b^3\\ [6pt]
&\ text {像术语一样合并。} & & a^3−b^3\ end {align*}\)

示例\(\PageIndex{23}\)

简化：\((x^3−x^2y)\;−\;(xy^2+y^3)\;+\;(x^2y+xy^2)\)

回答

\(x^3+y^3\)

示例\(\PageIndex{24}\)

简化：\((p^3−p^2q)\;+\;(pq^2+q^3)\;−\;(p^2q+pq^2)\)

回答

\(p^3−3p^2q+q^3\)

计算给定值的多项式函数

多项式函数是由多项式定义的函数。 例如，\(f(x)=x^2+5x+6\)和\(g(x)=3x−4\)是多项式函数，因为\(x^2+5x+6\)和\(3x−4\)是多项式。

定义：多项式函数

多项式函数是指其范围值由多项式定义的函数。

在 G raphs and Functions 中，我们首先引入了函数，我们了解到对一个函数\(f(x)\)进行求值意味着找出给定值的值\(x\)。 为了计算多项式函数，我们将用给定值代替变量，然后使用运算顺序进行简化。

示例\(\PageIndex{25}\)

对于该函数，请\(f(x)=5x^2−8x+4\)查找：

1. \(f(4)\)
2. \(f(−2)\)
3. \(f(0)\)。

回答

ⓐ

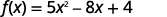
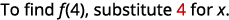
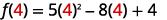
简化指数。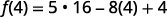
乘。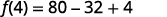
简化。

ⓑ

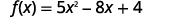
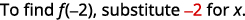
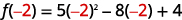
简化指数。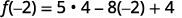
乘。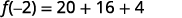
简化。

ⓒ

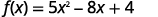
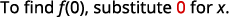
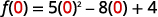
简化指数。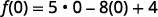
乘。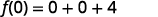

示例\(\PageIndex{26}\)

对于该函数\(f(x)=3x^2+2x−15\)，请找到

1. \(f(3)\)
2. \(f(−5)\)
3. \(f(0)\)。

回答

ⓐ 18 ⓑ 50 ⓒ\(−15\)

示例\(\PageIndex{27}\)

对于该函数\(g(x)=5x^2−x−4\)，请找到

1. \(g(−2)\)
2. \(g(−1)\)
3. \(g(0)\)。

回答

ⓐ 20 ⓑ 2 ⓒ\(−4\)

与下一个示例中的多项式函数相似的多项式函数用于许多领域，用于确定物体投影到空中后某个时候的高度。 下一个函数中的多项式专门用于从 250 英尺处掉落某物。

示例\(\PageIndex{28}\)

多项式函数\(h(t)=−16t^2+250\)给出了球从 250 英尺高的建筑物掉落后 t 秒的高度。 在\(t=2\)几秒钟后找到高度。

回答

\( \begin{array} {ll} {} &{h(t)=−16t^2+250} \\ {} &{} \\ {\text{To find }h(2)\text{, substitute }t=2.} &{h(2)=−16(2)^2+250} \\ {\text{Simplify.}} &{h(2)=−16·4+250} \\ {} &{}\\ {\text{Simplify.}} &{h(2)=−64+250} \\ {} &{} \\ {\text{Simplify.}} &{h(2)=186} \\ {} &{\text{After 2 seconds the height of the ball is 186 feet.}} \\ \end{array} \nonumber \)

示例\(\PageIndex{29}\)

多项式函数\(h(t)=−16t^2+150\)给出石头从 150 英尺高的悬崖上掉落后 t 秒的高度。 在\(t=0\)秒后找到高度（物体的初始高度）。

回答

高度是\(150\)英尺。

示例\(\PageIndex{30}\)

多项式函数\(h(t)=−16t^2+175\)给出了球从 175 英尺高的桥上掉落后 t 秒的高度。 在\(t=3\)几秒钟后找到高度。

回答

高度是\(31\)英尺。

加减多项式函数

就像可以加减多项式一样，也可以加减多项式函数。

定义：多项式函数的加减法

对于函数\(f(x)\)和\(g(x)\)，

\[(f+g)(x)=f(x)+g(x)\]

\[(f−g)(x)=f(x)−g(x)\]

示例\(\PageIndex{31}\)

对于函数\(f(x)=3x^2−5x+7\)和\(g(x)=x^2−4x−3\)，请查找：

1. \((f+g)(x)\)
2. \((f+g)(3)\)
3. \((f−g)(x)\)
4. \((f−g)(−2)\)。

回答

ⓐ

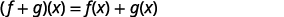
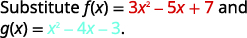
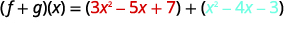
重写时不带括号。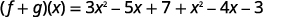
将相似的术语放在一起。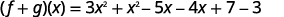
将相似的术语组合在一起。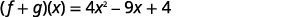

ⓑ 在 (a) 部分中，我们找到了\((f+g)(x)\)，现在被要求找到\((f+g)(3)\)。

\( \begin{array} {ll} {} &{(f+g)(x)=4x^2−9x+4} \\ {} &{} \\ {\text{To find }(f+g)\space(3),\text{ substitute }x=3.} &{(f+g)(3)=4(3)^2−9·3+4} \\ {} &{} \\ {} &{(f+g)(3)=4·9−9·3+4} \\ {} &{} \\ {} &{(f+g)(3)=36−27+4} \\ \end{array} \nonumber \)

请注意，我们可以\((f+g)(3)\)通过先\(g(3)\)分别找到\(f(3)\)和的值，然后将结果相加来找到。

查找\(f(3)\)。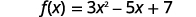
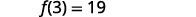
查找\(g(3)\)。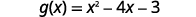
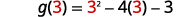
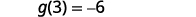
查找\((f+g)(3)\)。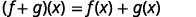

ⓒ

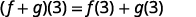
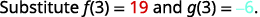
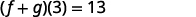
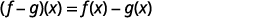
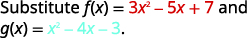
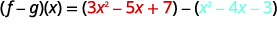
重写时不带括号。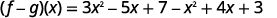
将相似的术语放在一起。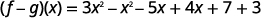
将相似的术语组合在一起。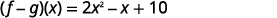

ⓓ

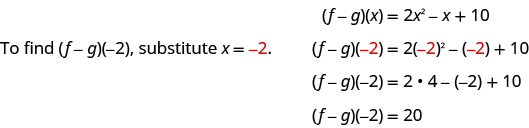
示例\(\PageIndex{32}\)

对于函数\(f(x)=2x^2−4x+3\)和\(g(x)=x^2−2x−6\)，请查找：ⓐ\((f+g)(x)\) ⓑ\((f+g)(3)\) ⓒ\((f−g)(x)\) ⓓ\((f−g)(−2)\)。

回答

ⓐ\((f+g)(x)=3x^2−6x−3\)

ⓑ\((f+g)(3)=6\)

ⓒ\((f−g)(x)=x^2−2x+9\)

ⓓ\((f−g)(−2)=17\)

示例\(\PageIndex{33}\)

对于函数\(f(x)=5x^2−4x−1\)和\(g(x)=x^2+3x+8\)，请查找 ⓐ\((f+g)(x)\) ⓑ\((f+g)(3)\) ⓒ\((f−g)(x)\) ⓓ\((f−g)(−2)\)。

回答

ⓐ\((f+g)(x)=6x^2−x+7\)

ⓑ\((f+g)(3)=58\)

ⓒ\((f−g)(x)=4x^2−7x−9\)

ⓓ\((f−g)(−2)=21\)

访问此在线资源，获取有关加减多项式的更多指导和练习。

• 加减多项式

关键概念

• 单项式
  • 单项式是具有一个项的代数表达式。
  • 一个变量中的单项式是 axm axm 形式的项，其中 a 是常数，m 是整数。
• 多项式
  • 多项式 —由加法或减法组合的单项式或两个或多个代数项是多项式。
  • 单项式 —只有一个项的多项式称为单项式。
  • 二项式 — 正好有两个项的多项式称为二项式。
  • 三项式 —正好有三个项的多项式称为三项式。
• 多项式的次数
  • 项的度数是其变量的指数之和。
  • 常数的度数为 0。
  • 多项式的次数是其所有项的最高度。

词汇表

二项式

二项式是正好有两个项的多项式。

常数的度

任何常数的度数均为 0。

多项式的次数

多项式的次数是其所有项的最高度。

一个术语的学位

项的度数是其变量的指数之和。

单项式

单项式是具有一个项的代数表达式。 一个变量中的单项式是 axm axm 形式的项，其中 a 是常数，m 是整数。

多项式

通过加法或减法组合的单项式或两个或多个单项式是多项式。

多项式的标准形式

当多项式的项按度降序书写时，多项式为标准形式。

三项式

三项式是正好有三个项的多项式。

多项式函数

多项式函数是指其范围值由多项式定义的函数。