4.8E：练习

Last updated
Save as PDF

Page ID: 203905

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

练习成就完美

确定有序对是否为线性不等式组的解

在以下练习中，确定每个有序对是否是系统的解。

1。 $\left\{\begin{array} {l} 3x+y>5\\2x−y\leq 10\end{array}\right.$

ⓐ$(3,−3)$
ⓑ$(7,1)$

2。 $\left\{\begin{array} {l} 4x−y<10\\−2x+2y>−8\end{array}\right.$

ⓐ$(5,−2)$
ⓑ$(−1,3)$

回答: ⓐ false ⓑ 真的

3。 $\left\{\begin{array} {l} y>\frac{2}{3}x−5\\x+\frac{1}{2}y\leq 4\end{array}\right.$

ⓐ$(6, −4)$
ⓑ$(3, 0)$

4。 $\left\{\begin{array} {l} y<\frac{3}{2}x+3\\ \frac{3}{4}x−2y<5\end{array}\right.$

ⓐ$(−4,−1)$
ⓑ$(8, 3)$

回答: ⓐ false ⓑ 真的

5。 $\left\{\begin{array} {l} 7x+2y>14\\5x−y\leq 8\end{array}\right.$

ⓐ$(2, 3)$
ⓑ$(7, −1)$

6。 $\left\{\begin{array} {l} 6x−5y<20\\−2x+7y>−8 \end{array}\right.$

ⓐ$(1, −3)$
ⓑ$(−4, 4)$

回答: ⓐ false ⓑ 真的

通过绘图求解线性不等式系统

在以下练习中，通过绘图求解每个系统。

7。 $\left\{\begin{array} {l} y\leq 3x+2\\y>x−1\end{array}\right.$

8。 $\left\{\begin{array} {l} y<−2x+2\\y\geq −x−1\end{array}\right.$

回答

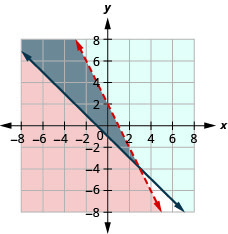
$该图显示了不等式 y 小于负两倍 x 加二，y 大于或等于负 x 减一的图形。显示了两条相交线，一条为红色，另一条为蓝色。两条线所边界的区域以灰色显示。$

解决方案是灰色区域。

9。 $\left\{\begin{array} {l} y<2x−1\\y\leq −\frac{1}{2}x+4\end{array}\right.$

10。 $\left\{\begin{array} {l} y\geq −\frac{2}{3}x+2\\y>2x−3\end{array}\right.$

回答

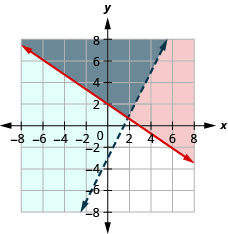
$该图显示了不等式 y 大于或等于减二乘三 x 加二，y 大于两倍 x 减三的图形。显示了两条相交线，一条为红色，另一条为蓝色。它们所绑定的区域以灰色显示。$

解决方案是灰色区域。

11。 $\left\{\begin{array} {l} x−y>1\\y<−\frac{1}{4}x+3\end{array}\right.$

12。 $\left\{\begin{array} {l} x+2y<4\\y<x−2\end{array}\right.$

回答

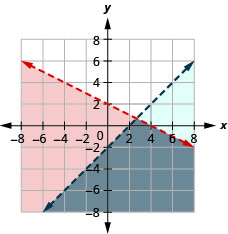
$该图显示了不等式 x 减两倍 y 小于四和 y 小于 x 减二的图形。显示了两条相交线，一条为蓝色，另一条为红色。线条边界的区域以灰色显示。$

解决方案是灰色区域。

13。 $\left\{\begin{array} {l} 3x−y\geq 6\\y\geq −\frac{1}{2}x\end{array}\right.$

14。 $\left\{\begin{array} {l} x+4y\geq 8\\y\leq \frac{3}{4}x\end{array}\right.$

回答

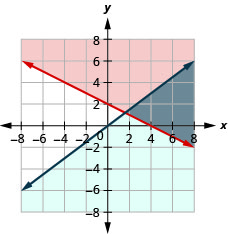
$该图显示了不等式两倍 x 加四倍 y 大于或等于 8，y 小于或等于 x 的负四分之三。显示了两条相交线，一条为蓝色，另一条为红色。线条边界的区域以灰色显示。这是解决方案。$

解决方案是灰色区域。

15。 $\left\{\begin{array} {l} 2x−5y<10\\3x+4y\geq 12\end{array}\right.$

16。 $\left\{\begin{array} {l} 3x−2y\leq 6\\−4x−2y>8\end{array}\right.$

回答

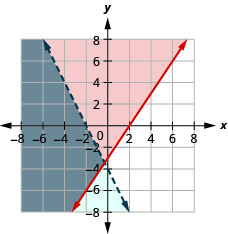
$该图显示了不等式三倍 x 减去两倍 y 小于或等于六和减四倍 x 减去两倍 y 大于八的图形。显示了两条相交线，一条为蓝色，另一条为红色。线条边界的区域以灰色显示。这是解决方案。$

解决方案是灰色区域。

17。 $\left\{\begin{array} {l} 2x+2y>−4\\−x+3y\geq 9\end{array}\right.$

18。 $\left\{\begin{array} {l} 2x+y>−6\\−x+2y\geq −4\end{array}\right.$

回答

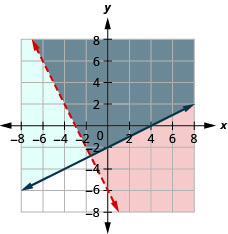
$该图显示了不等式两倍 x 加 y 大于负六和负 x 加两倍 y 大于或等于负四的图形。显示了两条相交线，一条为蓝色，另一条为红色。线条边界的区域以灰色显示。这是解决方案。$

解决方案是灰色区域。

19。 $\left\{\begin{array} {l} x−2y<3\\y\leq 1\end{array}\right.$

20。 $\left\{\begin{array} {l} x−3y>4\\y\leq −1\end{array}\right.$

回答

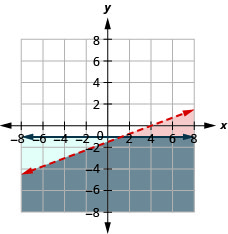
$该图显示了不等式 x 减三倍 y 大于四和 y 小于或等于负一的图形。显示了两条相交线，一条为蓝色，另一条为红色。线条边界的区域以灰色显示。这是解决方案。$

解决方案是灰色区域。

21。 $\left\{\begin{array} {l} y\geq −\frac{1}{2}x−3\\x\leq 2\end{array}\right.$

22。 $\left\{\begin{array} {l} y\leq −\frac{2}{3}x+5\\x\geq 3\end{array}\right.$

回答

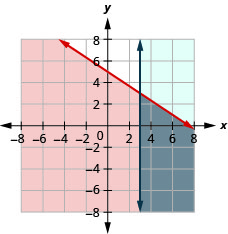
$该图显示了不等于 y 小于或等于负二乘以三乘以 x 加五，x 大于或等于三的图形。显示了两条相交线，一条为蓝色，另一条为红色。线条边界的区域以灰色显示。这是解决方案。$

解决方案是灰色区域。

23。 $\left\{\begin{array} {l} y\geq \frac{3}{4}x−2\\y<2\end{array}\right.$

24。 $\left\{\begin{array} {l} y\leq −\frac{1}{2}x+3\\y<1\end{array}\right.$

回答

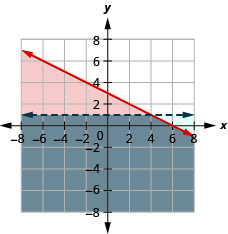
$该图显示了不等于 y 小于或等于负一半 x 加三和 y 小于一的图形。显示了两条相交线，一条为蓝色，另一条为红色。线条边界的区域以灰色显示。这是解决方案。$

解决方案是灰色区域。

25。 $\left\{\begin{array} {l} 3x−4y<8\\x<1\end{array}\right.$

26。 $\left\{\begin{array} {l} −3x+5y>10\\x>−1\end{array}\right.$

回答

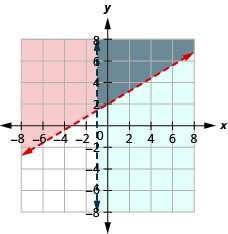
$该图显示了不等式减三倍 x 加五倍 y 大于十和 x 大于负一的图形。显示了两条相交线，一条为蓝色，另一条为红色。线条边界的区域以灰色显示。这是解决方案。$

解决方案是灰色区域。

27。 $\left\{\begin{array} {l} x\geq 3\\y\leq 2\end{array}\right.$

28。 $\left\{\begin{array} {l} x\leq −1\\y\geq 3\end{array}\right.$

回答

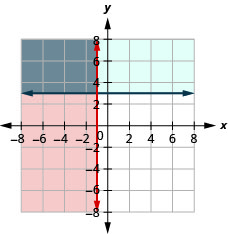
$该图显示了不等式 x 小于或等于负一，y 大于或等于三的图形。显示了两条相交线，一条为蓝色，另一条为红色。线条边界的区域以灰色显示。这是解决方案。$

解决方案是灰色区域。

29。 $\left\{\begin{array} {l} 2x+4y>4 \\ y\leq −\frac{1}{2}x−2\end{array}\right.$

30。 $\left\{\begin{array} {l} x−3y\geq 6\\y>\frac{1}{3}x+1\end{array}\right.$

回答

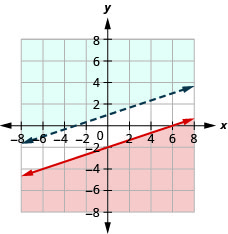
$该图显示了不等式 x 减去三倍 y 大于或等于 6，y 大于 x 加一的三分之一的图形。显示了两条非相交线，一条为蓝色，另一条为红色。$

没有解决办法。

31。 $\left\{\begin{array} {l} −2x+6y<0\\6y>2x+4\end{array}\right.$

32。 $\left\{\begin{array} {l} −3x+6y>12\\4y\leq 2x−4\end{array}\right.$

回答

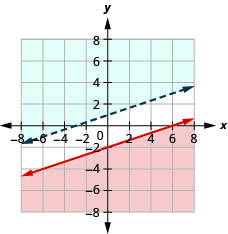
$该图显示了不等式减三倍 x 加六倍 y 大于十二和四倍 y 小于或等于两倍 x 减去四的图形。显示了两条非相交线，一条为蓝色，另一条为红色。$

没有解决办法。

33。 $\left\{\begin{array} {l} y\geq −3x+2\\3x+y>5\end{array}\right.$

34。 $\left\{\begin{array} {l} y\geq \frac{1}{2}x−1\\−2x+4y\geq 4\end{array}\right.$

回答

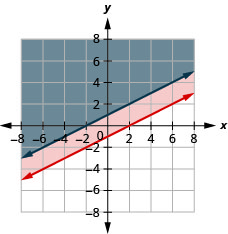
$该图显示了不等于 y 大于或等于减半 x 减一和减两倍 x 加四倍 y 大于或等于四的图形。显示了两条非相交线，一条为蓝色，另一条为红色。解决方案区域以灰色显示。$

解决方案是灰色区域。

35。 $\left\{\begin{array} {l} y\leq −\frac{1}{4}x−2\\x+4y<6\end{array}\right.$

36。 $\left\{\begin{array} {l} y\geq 3x−1\\−3x+y>−4\end{array}\right.$

回答

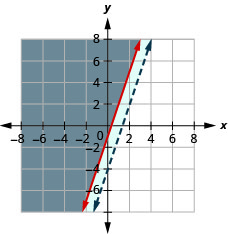
$该图显示了不等于 y 大于或等于三倍 x 减一和负三倍 x 加 y 大于负四的图形。显示了两条非相交线，一条为蓝色，另一条为红色。解决方案区域以灰色显示。$

解决方案是灰色区域。

37。 $\left\{\begin{array} {l} 3y>x+2\\−2x+6y>8\end{array}\right.$

38。 $\left\{\begin{array} {l} y<\frac{3}{4}x−2\\−3x+4y<7\end{array}\right.$

回答

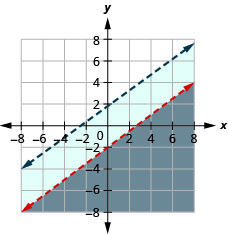
$该图显示了不等式 y 小于三乘以四分之一 x 减二和减三 x 加四 y 小于七的图表。显示了两条非相交线，一条为蓝色，另一条为红色。解决方案区域以灰色显示。$

解决方案是灰色区域。

求解不等式系统的应用

在以下练习中，转化为不等式系统并求解。

39。凯特琳在县集市上出售她的画作。她想卖至少60幅画，还有肖像画和风景画。她以15美元的价格出售肖像，以10美元的价格出售风景。她需要出售至少价值800美元的图纸才能获利。

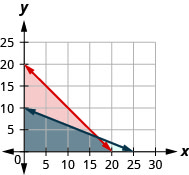
40。杰克不想花超过50美元购买一袋肥料和泥炭苔作为自己的花园。肥料每袋花费2美元，泥炭苔每袋花5美元。杰克的货车最多可以容纳 20 个袋子。

回答

ⓐ$\left\{\begin{array} {l} f\geq 0 \\ p\geq 0 \\ f+p\leq 202 \\ f+5p\leq 50\end{array}\right.$
ⓑ

$该图显示了不等式 f 加 p 小于或等于二十和二 f 和五 p 小于或等于五十的图。显示了两条相交线，一条为蓝色，另一条为红色。区域以灰色显示。$

ⓒ 是的
ⓓ 不

41。 Reiko 需要邮寄她的圣诞贺卡和包裹，并希望将邮寄费用保持在不超过 500 美元。卡片的数量至少为 4 张，是包装数量的两倍多。邮寄卡片（附上图片）的费用为3美元，包裹的邮寄费用为7美元。

42。胡安正在学习化学和代数的期末考试。他知道自己只有 24 小时的学习时间，而且学习代数所需的时间至少是化学的三倍。

回答

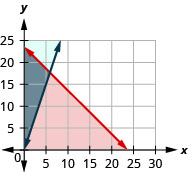
ⓐ$\left\{\begin{array} {l} c\geq 0\\a\geq 0\\c+a\leq 24\\a\geq 3c\end{array}\right.$
ⓑ

$该图显示了不等式 c 加上小于或等于二十四和 a 大于或等于三倍 c 的图形。显示了两条相交线，一条为蓝色，另一条为红色。区域以灰色显示。$

ⓒ 是的
ⓓ 不

43。 Jocelyn 怀孕了，所以她每天需要比平时多摄入至少 500 卡路里的热量。有一天，当她以15美元的预算购买额外食物时，她会购买每根含有90卡路里的香蕉和每根含有150卡路里的巧克力格兰诺拉麦片棒。香蕉每根售价0.35美元，格兰诺拉麦片棒每根售价2.50美元。

44。马克正在尝试增加肌肉质量，因此他每天至少需要多吃80克蛋白质。一瓶蛋白水的价格为3.20美元，一瓶蛋白棒的价格为1.75美元。蛋白水提供 27 克蛋白质，棒提供 16 克蛋白质。如果他有10美元可以花

回答

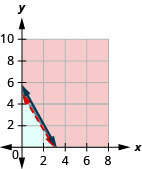
ⓐ$\left\{\begin{array} {l} w\geq 0\\b\geq 0\\27w+16b>80\\3.20w+1.75b\leq 10\end{array}\right.$
ⓑ

$该图显示了不等式二十七倍 w 加十六倍 b 大于八十和三点二倍 w 加一点七五 b 小于或等于十的图。显示了两条相交线，一条为蓝色，另一条为红色。区域以灰色显示。$

ⓒ 不
ⓓ 是的

45。 Jocelyn 希望增加蛋白质消耗量和卡路里摄入量。她希望每天至少多摄取35克蛋白质，每天额外摄取不超过200卡路里的热量。一盎司的切达干酪含有 7 克蛋白质和 110 卡路里的热量。一盎司的帕尔马干酪含有 11 克蛋白质和 22 卡路里的热量。

46。 Mark 通过每天至少跑步和步行 4 英里来增加锻炼习惯。他的目标是从这项运动中消耗至少 1500 卡路里的热量。步行每英里消耗 270 卡路里，跑步消耗 650 卡路里的热量。

回答

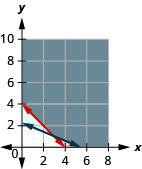
ⓐ$\left\{\begin{array} {l} w\geq 0\\r\geq 0\\w+r\geq 4\\270w+650r\geq 1500\end{array}\right.$
ⓑ

$该图显示了不等式 w 加 r 大于或等于四和二七十 w 加上六五十 r 大于或等于一千五百的图表。显示了两条相交线，一条为蓝色，另一条为红色。区域以灰色显示。$

ⓒ 不
ⓓ 是的

写作练习

47。绘制不等式的图表$x−y\geq 3$。你怎么知道这条线的哪一边$x−y=3$应该加上阴影？

48。绘制系统图表$\left\{\begin{array} {l} x+2y\leq 6 \\ y\geq −\frac{1}{2}x−4\end{array}\right.$。解决方案是什么意思？

回答: 答案会有所不同。

自检

ⓐ 完成练习后，使用这份清单来评估你对本节目标的掌握程度。

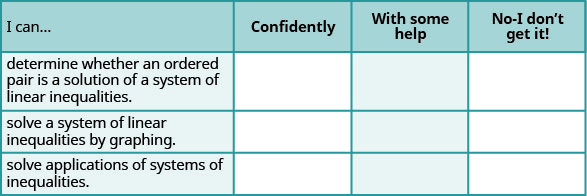
$该图显示了一个包含四列四行的表。第一行是标题行。这四个标题我可以... 自信地说，需要一些帮助，不是 — 我不明白！在第一列的第二行中，文本显示 “确定有序对是否是线性不等式组的解”。在第一列的第三行中，文中写着 “求解不等式系统的应用”。$

ⓑ 这份清单告诉你你对本部分的掌握情况了什么？你会采取哪些措施来改进？