第 4 章复习练习

章节复习练习

求解具有两个变量的线性方程组

确定有序对是否是方程组的解。

在以下练习中，确定以下点是否为给定方程组的解。

1。 $\left\{ \begin{array} {l} x+3y=−9\\2x−4y=12 \end{array} \right.$

ⓐ$(−3,−2)$
ⓑ$(0,−3)$

2。 $\left\{ \begin{array} {l} x+y=8\\y=x−4 \end{array} \right.$

ⓐ$(6,2)$
ⓑ$(9,−1)$

回答

ⓐ 是的 ⓑ 不

通过绘图求解线性方程组

在以下练习中，通过绘图求解以下方程组。

3。 $\left\{ \begin{array} {l} 3x+y=6\\x+3y=−6 \end{array} \right.$

4。 $\left\{ \begin{array} {l} x+4y=−1\\x=3 \end{array} \right.$

回答

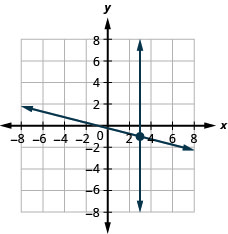
$(3,−1)$

5。 $\left\{ \begin{array} {l} 2x−y=5\\4x−2y=10 \end{array} \right.$

6。 $\left\{ \begin{array} {l} −x+2y=4\\y=\frac{1}{2}x−3 \end{array} \right.$

回答

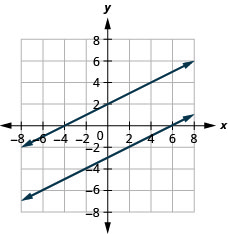
没有解决办法

在以下练习中，无需绘制图即可确定解的数量，然后对方程组进行分类。

7。 $\left\{ \begin{array} {l} y=\frac{2}{5}x+2\\−2x+5y=10 \end{array} \right.$

8。 $\left\{ \begin{array} {l} 3x+2y=6\\y=−3x+4 \end{array} \right.$

回答

一个解，一致方程，独立方程

9。 $\left\{ \begin{array} {l} 5x−4y=0\\y=\frac{5}{4}x−5 \end{array} \right.$

通过替换求解方程组

在以下练习中，通过替换求解方程组。

10。 $\left\{ \begin{array} {l} 3x−2y=2\\y=\frac{1}{2}x+3 \end{array} \right.$

回答

$(4,5)$

11。 $\left\{ \begin{array} {l} x−y=0\\2x+5y=−14 \end{array} \right.$

12。 $\left\{ \begin{array} {l} y=−2x+7\\y=\frac{2}{3}x−1 \end{array} \right.$

回答

$(3,1)$

13。 $\left\{ \begin{array} {l} y=−5x\\5x+y=6 \end{array} \right.$

14。 $\left\{ \begin{array} {l} y=−\frac{1}{3}x+2\\x+3y=6 \end{array} \right.$

回答

无限多的解决方案

通过消除求解方程组

在以下练习中，通过消除求解方程组

15。 $\left\{ \begin{array} {l} x+y=12\\x−y=−10 \end{array} \right.$

16。 $\left\{ \begin{array} {l} 3x−8y=20\\x+3y=1 \end{array} \right.$

回答

$(4,−1)$

17。 $\left\{ \begin{array} {l} 9x+4y=2\\5x+3y=5 \end{array} \right.$

18。 $\left\{ \begin{array} {l} \frac{1}{3}x−\frac{1}{2}y=1\\ \frac{3}{4}x−y=\frac{5}{2} \end{array} \right.$

回答

$(6,2)$

19。 $\left\{ \begin{array} {l} −x+3y=8\\2x−6y=−20 \end{array} \right.$

选择最方便的方法来求解线性方程组

在以下练习中，决定通过替换或消法求解方程组是否更方便。

20。 $\left\{ \begin{array} {l} 6x−5y=27\\3x+10y=−24 \end{array} \right.$

回答

消除

21。 $\left\{ \begin{array} {l} y=3x−9\\4x−5y=23 \end{array} \right.$

使用方程组求解应用程序

解决直接翻译应用程序

在以下练习中，转换为方程组并求解。

22。 莫莉想在她的花园里种200个球茎，全部是虹膜和郁金香。 她想种的郁金香数量是虹膜的三倍。 她应该种多少虹膜和多少郁金香？

回答

50 朵虹膜和 150 朵郁金香

23。 两家电话公司向阿散蒂提供了职位。 第一家公司支付22,000美元的薪水，外加每售出一张合约100美元的佣金。 第二个支付28,000美元的工资，外加每售出合约25美元的佣金。 需要出售多少合同才能使总薪水保持不变？

24。 勒罗伊花了 20 分钟慢跑，40 分钟骑自行车，消耗了 600 卡路里的热量。 第二天，勒罗伊交换了时间，慢跑了40分钟，骑了20分钟，消耗了相同数量的卡路里。 每分钟慢跑消耗多少卡路里，骑行每分钟消耗多少卡路里？

回答

10 卡路里慢跑和 10 卡路里骑行

25。 特洛伊和丽莎正在购买学校用品。 每个人购买了不同数量的相同笔记本电脑和计算器。 特洛伊以116美元的价格购买了四台笔记本电脑和五台计算器。 丽莎花了68美元买了两台笔记本和三台计算器。 找出每台笔记本电脑和每个闪存盘的成本。

求解几何应用程序

在以下练习中，转换为方程组并求解。

26。 两个补充角度的差为 58 度。 找到角度的测量值。

回答

119、61

27。 两个角度是互补的。 较大角度的测量值是小角度的四倍以上的五倍。 找到两个角度的测量值。

28。 直角三角形中一个小角度的测量值小于 15，小于另一个小角度的两倍。 找到两个角度的测量值。

回答

$35°$和$55°$

29。 Becca 在凉棚的两侧和顶部挂着一个 28 英尺长的花环，为婚礼做准备。 高度比宽度小四英尺。 找出凉棚的高度和宽度。

30。 城市矩形公园的周长为 1428 英尺。 长度为 78 英尺，是宽度的两倍多。 找出公园的长度和宽度。

回答

长度为 450 英尺，宽度为 264 英尺

求解均匀运动应用程序

在以下练习中，转换为方程组并求解。

31。 希拉和莱诺尔正开车去他们祖母家。 莱诺尔在希拉一小时后离开了。 希拉以每小时 45 英里的速度行驶，莱诺尔以 60 英里/小时的速度行驶。 莱诺尔要花多长时间才能赶上希拉？

32。 鲍勃离开家，以每小时 10 英里的速度骑自行车去湖边。 他的妻子谢丽尔在45分钟（34（34 小时）后离开，以每小时25英里的速度开车。 谢丽尔要花多长时间才能赶上鲍勃？

回答

$12$一小时

33。 马库斯可以在三个小时内将他的船开到河边 36 英里，但要花四个小时才能返回上游。 找出船在静止水中的速度和水流的速率。

34。 客机可以顺风在 2 小时内飞行 804 英里，但逆风后的 2 小时内只能飞行 776 英里。 找出喷气机在静止空气中的速度和风速。

回答

喷气式飞机的速度为 395 英里/小时，风速为 7 英里/小时

使用方程组求解混合应用

使用方程组求解混合应用

在以下练习中，转换为方程组并求解。

35。 林恩总共花了2780美元购买了261张剧院门票。 学生票价为10美元，成人票为15美元。 Lynn 买了多少张学生票和多少张成人票？

36。 Priam 车里的杯架里有毛钱和便士。 这些硬币的总价值为4.21美元。 硬币的数量比便士数少四倍。 杯子里有多少毛钱和多少便士？

回答

41 毛钱和 11 便士

37。 Yumi 想用糖果和坚果制作 12 杯派对混合物。 她的预算要求派对组合花费她每杯1.29美元。 糖果每杯2.49美元，坚果每杯0.69美元。 她应该用多少杯糖果和多少杯坚果？

38。 科学家需要 70 升 40% 的酒精溶液。 他有 30% 和 60% 的解决方案可用。 要制成 40% 的溶液，他应该混合多少升和 60% 溶液中的多少升？

回答

$46\frac{2}{3}$升 30% 溶液，$23\frac{1}{3}$升 60% 溶液

解决利息申请

在以下练习中，转换为方程组并求解。

39。 杰克有12,000美元可以投资，并希望每年赚取7.5％的利息。 他将把一部分钱存入年收入4％的储蓄账户，其余存入年收入9％的存款证账户。 他应该向每个账户存多少钱？

40。 当琳达大学毕业时，她将欠43,000美元的学生贷款。 联邦贷款的利率为4.5％，私人银行贷款的利率为2％。 她一年的总利息为1,585美元。 每笔贷款的金额是多少？

回答

联邦贷款29,000美元，私人贷款14,000美元

求解具有三个变量的方程组

求解具有三个变量的方程组

在以下练习中，确定订购的三元组是否是系统的解决方案。

41。 $\left\{ \begin{array} {l} 3x−4y−3z=2\\2x−6y+z=3\\2x+3y−2z=3 \end{array} \right.$

ⓐ$(2,3,−1)$
ⓑ$(3,1,3)$

42。 $\left\{ \begin{array} {l} y=\frac{2}{3}x−2\\x+3y−z=15\\x−3y+z=−2 \end{array} \right.$

ⓐ$(−6,5,\frac{1}{2})$
ⓑ$(5,\frac{4}{3},−3)$

回答

ⓐ 不 ⓑ 是的

求解具有三个变量的线性方程组

在以下练习中，求解方程组。

43。 $\left\{ \begin{array} {l} 3x−5y+4z=5\\5x+2y+z=0\\2x+3y−2z=3 \end{array} \right.$

44。 $\left\{ \begin{array} {l} x+\frac{5}{2}y+z=−2\\2x+2y+\frac{1}{2}z=−4\\ \frac{1}{3}x−y−z=1 \end{array} \right.$

回答

$(−3,2,−4)$

45。 $\left\{ \begin{array} {l} 5x+3y=−6\\2y+3z=−1\\7x+z=1 \end{array} \right.$

46。 $\left\{ \begin{array} {l} 2x+3y+z=12\\x+y+z=9\\3x+4y+2z=20 \end{array} \right.$

回答

没有解决办法

47。 $\left\{ \begin{array} {l} −x−3y+2z=14\\−x+2y−3z=−4\\3x+y−2z=6 \end{array} \right.$

使用具有三个变量的线性方程组求解应用程序

48。 参加美国职业棒球大联盟比赛后，顾客经常购买纪念品。 如果一个家庭购买 4 件 T 恤、一顶帽子和 1 只毛绒玩具，则总额为 135 美元。 一对夫妇为侄女买了 2 件 T 恤、一顶帽子和 3 只毛绒玩具，花了 115 美元。 另一对夫妇购买了 2 件 T 恤、一顶帽子和 1 只毛绒玩具，总价为 85 美元。 每件商品的成本是多少？

回答

$25, 20, 15$

使用矩阵求解方程组

为方程组编写增强矩阵。

将每个线性方程组写成增强矩阵。

49。 $\left\{ \begin{array} {l} 3x−y=−1\\−2x+2y=5 \end{array} \right.$

50。 $\left\{ \begin{array} {l} 4x+3y=−2\\x−2y−3z=7\\2x−y+2z=−6 \end{array} \right.$

回答

$\left[ \begin{matrix} 4&3&0&−2\\1&−2&−3&7\\2&−1&2&−6 \end{matrix} \right]$

写出与增强矩阵对应的方程组。

51。 $\left[ \begin{array} {cc|c} 2&−4&-2\\3&−3&-1 \end{array} \right]$

52。 $\left[ \begin{array} {ccc|c} 1&0&−3&-1\\1&−2&0&-2\\0&−1&2&3 \end{array} \right]$

回答

$\left\{ \begin{array} {l} x−3z=−1\\x−2y=−27\\−y+2z=3 \end{array} \right.$

在以下练习中，对增强矩阵执行指定的运算。

53。 $\left[ \begin{array} {cc|c} 4&−6&-3\\3&2&1 \end{array} \right]$

ⓐ 交换第 2 行和第 1 行。
ⓑ 将第 1 行乘以 4。
ⓒ 将第 2 行乘以 3 并相加到第 1 行。

54。 $\left[ \begin{array} {ccc|c} 1&−3&−2&4\\2&2&−1&-3\\4&−2&−3&-1 \end{array} \right]$

ⓐ 互换第 2 行和第 3 行。
ⓑ 将第 1 行乘以 2。
ⓒ 将第 3 行乘以 −2−2，然后与第 2 行相加。

回答

ⓐ$\left[ \begin{matrix} 1&−3&−2&4\\4&−2&−3&−1\\2&2&−1&−3 \end{matrix} \right]$

ⓑ$\left[ \begin{matrix} 2&−6&−4&8\\4&−2&−3&−1\\2&2&−1&−3 \end{matrix} \right]$

ⓒ$\left[ \begin{matrix} 2&−6&−4&8\\4&−2&−3&−1\\0&−6&−1&5 \end{matrix} \right]$

使用矩阵求解方程组

在以下练习中，使用矩阵求解每个方程组。

55。 $\left\{ \begin{array} {l} 4x+y=6\\x−y=4 \end{array} \right.$

56。 $\left\{ \begin{array} {l} 2x−y+3z=−3\\−x+2y−z=10\\x+y+z=5 \end{array} \right.$

回答

$(−2,5,−2)$

57。 $\left\{ \begin{array} {l} 2y+3z=−1\\5x+3y=−6\\7x+z=1 \end{array} \right.$

58。 $\left\{ \begin{array} {l} x+2y−3z=−1\\x−3y+z=1\\2x−y−2z=2 \end{array} \right.$

回答

没有解决办法

59。 $\left\{ \begin{array} {l} x+y−3z=−1\\y−z=0\\−x+2y=1 \end{array} \right.$

使用行列式求解方程组

计算 2 × 2 矩阵的行列式

在以下练习中，计算方矩阵的确定值。

60。 $\left[ \begin{matrix} 8&−4\\5&−3 \end{matrix} \right]$

回答

$−4$

计算 3×3 矩阵的行列式

在以下练习中，找到并评估指定的未成年人。

61。 $\left| \begin{matrix} −1&−3&2\\4&−2&−1\\−2&0&−3 \end{matrix} \right|$; 找到未成年人 ⓐ$a_1$ ⓑ$b_1$ ⓒ$c_2$

在接下来的练习中，通过沿第一行按未成年人扩展来评估每个决定因素。

62。 $\left| \begin{matrix} −2&−3&−4\\5&−6&7\\−1&2&0 \end{matrix} \right|$

回答

$21$在接下来的练习中，通过按未成年人扩展来评估每个决定因素。

63。 $\left| \begin{matrix} 3&5&4\\−1&3&0\\−2&6&1 \end{matrix} \right|$

使用克莱默法则求解方程组

在以下练习中，使用克莱默法则求解每个方程组

64。 $\left\{ \begin{array} {l} x−3y=−9\\2x+5y=4 \end{array} \right.$

回答

$(−3,2)$

65。 $\left\{ \begin{array} {l} 4x−3y+z=7\\2x−5y−4z=3\\3x−2y−2z=−7 \end{array} \right.$

66。 $\left\{ \begin{array} {l} 2x+5y=4\\3y−z=3\\4x+3z=−3 \end{array} \right.$

回答

$(−3,2,3)$

67。 $\left\{ \begin{array} {l} x+y−3z=−1\\y−z=0\\−x+2y=1 \end{array} \right.$

68。 $\left\{ \begin{array} {l} 3x+4y−3z=−2\\2x+3y−z=−1\\2x+y−2z=6 \end{array} \right.$

回答

不一致

使用决定因素求解应用程序

在以下练习中，确定给定点是否共线。

69。 $(0,2)$$(−1,−1)$、和$(−2,4)$

绘制线性不等式系统的图表

确定有序对是否为线性不等式组的解

在以下练习中，确定每个有序对是否是系统的解。

70。 $\left\{ \begin{array} {l} 4x+y>6\\3x−y\leq 12 \end{array} \right.$

ⓐ$(2,−1)$
ⓑ$(3,−2)$

回答

ⓐ 是的 ⓑ 不

71。 $\left\{ \begin{array} {l} y>\frac{1}{3}x+2\\x−\frac{1}{4}y\leq 10 \end{array} \right.$

ⓐ$(6,5)$
ⓑ$(15,8)$

通过绘图求解线性不等式系统

在以下练习中，通过绘图求解每个系统。

72。 $\left\{ \begin{array} {l} y<3x+1\\y\geq −x−2 \end{array} \right.$

回答

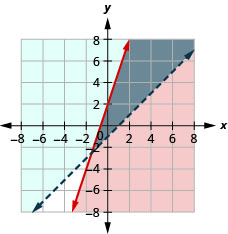
解决方案是灰色区域。

73。 $\left\{ \begin{array} {l} x−y>−1\\y<\frac{1}{3}x−2 \end{array} \right.$

74。 $\left\{ \begin{array} {l} 2x−3y<6\\3x+4y\geq 12 \end{array} \right.$

回答

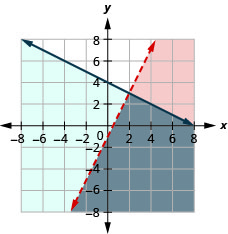
解决方案是灰色区域。

75。 $\left\{ \begin{array} {l} y\leq −\frac{3}{4}x+1\\x\geq −5 \end{array} \right.$

76。 $\left\{ \begin{array} {l} x+3y<5\\y\geq -\frac{1}{3}x+6 \end{array} \right.$

回答

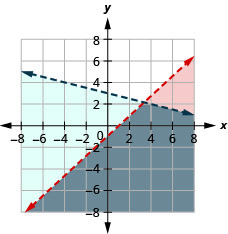
没有解决办法。

77。 $\left\{ \begin{array} {l} y\geq 2x−5\\−6x+3y>−4 \end{array} \right.$

求解不等式系统的应用

在以下练习中，转化为不等式系统并求解。

78。 Roxana 生产手链和项链，然后在农贸市场出售。 她以每条12美元的价格出售手链，每条18美元的价格出售项链。 下周末在市场上，她将有空间展示不超过40件作品，而且她需要卖出价值至少500美元才能获利。

ⓐ 编写一个不等式系统来模拟这种情况。
ⓑ 绘制系统图表。
ⓒ 她应该展示 26 条手链和 14 条项链吗？
ⓓ 她应该展示 39 条手链和 1 条项链吗？

回答

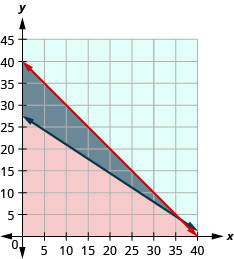
ⓐ$\left\{ \begin{array} {l} b\geq 0\\ n\geq 0\\ b+n\leq 40\\12b+18n\geq 500 \end{array} \right.$
ⓑ

ⓒ 是的
ⓓ 不

79。 安妮有600美元的预算为她的课堂购买平装书和精装书。 她希望精装书的数量至少是平装书数量的三倍多 5 本。 平装书每本售价4美元，精装书每本售价15美元。

ⓐ 编写一个不等式系统来模拟这种情况。
ⓑ 绘制系统图表。
ⓒ 她能买 8 本平装书和 40 本精装书吗？
ⓓ 她能买 10 本平装书和 37 本精装书吗？

章节练习测试

在以下练习中，通过绘图求解以下系统。

1。 $\left\{ \begin{array} {l} x−y=5\\x+2y=−4 \end{array} \right.$

回答

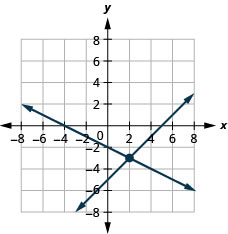
$(2,−3)$

2。 $\left\{ \begin{array} {l} x−y>−2\\y\leq 3x+1 \end{array} \right.$

在以下练习中，求解每个方程组。 使用替换或消除。

3。 $\left\{ \begin{array} {l} x+4y=6\\−2x+y=−3 \end{array} \right.$

回答

$(2,1)$

4。 $\left\{ \begin{array} {l} −3x+4y=2\\5x−5y=−23 \end{array} \right.$

5。 $\left\{ \begin{array} {l} x+y−z=−1\\2x−y+2z=8\\−3x+2y+z=−9 \end{array} \right.$

回答

$(2,−2,1)$

使用矩阵求解方程组。

6。 $\left\{ \begin{array} {l} 2x+y=7\\x−2y=6 \end{array} \right.$

7。 $\left\{ \begin{array} {l} −3x+y+z=−4\\−x+2y−2z=1\\2x−y−z=−1 \end{array} \right.$

回答

$(5,7,4)$

使用克莱默法则求解。

8。 $\left\{ \begin{array} {l} 3x+y=−3\\2x+3y=6 \end{array} \right.$

9。 通过扩大未成年人来评估决定因素：

$\left| \begin{matrix} 3&−2&−2\\2&−1&4\\−1&0&−3 \end{matrix} \right|$

回答

$99$

在以下练习中，转换为方程组并求解。

10。 格雷格正在上游划独木舟，逆流冲向 10 英里外的钓鱼点。 如果他在上游划桨2.5小时，回程需要1.25个小时，请在静水中找到潮流的速度和他的划桨速度。

11。 药剂师需要 20 升 2% 的盐溶液。 他有 1% 和 5% 的解决方案可用。 她应该混合多少升 1% 的溶液和 5% 的溶液中的多少升才能制成 2% 的溶液？

回答

15 升 1% 溶液，5 升 5% 溶液

12。 阿诺德投资了64,000美元，其中一些为5.5％的利息，其余为9％。 如果他在一年内获得4,500美元的利息，按每种利率投资了多少？

13。 教会青年团体正在出售零食，以筹集资金参加他们的会议。 艾米卖出了 2 磅糖果、3 盒饼干和 1 罐爆米花，总销售额为 65 美元。 布莱恩卖出了 4 磅糖果、6 盒饼干和 3 罐爆米花，总销售额为 140 美元。 宝琳娜售出了 8 磅糖果、8 盒饼干和 5 罐爆米花，总销售额为 250 美元。 每件商品的成本是多少？

回答

糖果的价格为20美元；饼干的价格为5美元；爆米花的价格为10美元。

14。 格兰诺拉麦棒的制造商花费1.20美元制作每块麦片，然后以2美元的价格出售。 制造商每月的固定成本也为8,000美元。

ⓐ 在制造 x 块格兰诺拉麦片棒时找到成本函数 C
ⓑ 售出 x 个格兰诺拉麦片棒时找到收入函数 R。
ⓒ 通过在同一个网格上绘制收入和成本函数的图表来显示盈亏平衡点。
ⓓ 找到盈亏平衡点。 解释盈亏平衡点的含义。

15。 转化为不平等体系并求解。

安迪想花不超过50美元购买万圣节零食。 她想购买每块花费1美元的糖棒和每块花费0.50美元的棒棒糖，她希望棒棒糖的数量至少是糖棒数量的三倍。

ⓐ 编写一个不等式系统来模拟这种情况。
ⓑ 绘制系统图表。
ⓒ 她能买 20 块糖和 40 根棒棒糖吗？

回答

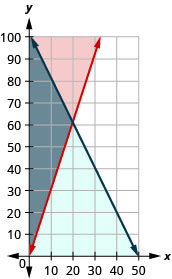
ⓐ$\left\{ \begin{array} {l} C\geq 0\\ L\geq 0\\ C+0.5L\leq 50 \\ L\geq 3C \end{array} \right.$
ⓑ

ⓒ 不
ⓓ 是的