4.7：使用行列式求解方程组

Last updated
Save as PDF

Page ID: 203894

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

学习目标

在本节结束时，您将能够：

计算 2×2 矩阵的行列式
计算 3×3 矩阵的行列式
使用克莱默法则求解方程组
使用决定因素求解应用程序

在开始之前，请参加这个准备测验。

简化：$5(−2)−(−4)(1)$。
如果你错过了这个问题，请查看 [链接]。
简化：$−3(8−10)+(−2)(6−3)−4(−3−(−4))$。
如果你错过了这个问题，请查看 [链接]。
简化：$\frac{−12}{−8}$。
如果你错过了这个问题，请查看 [链接]。

在本节中，我们将学习另一种求解线性方程组的方法，称为克莱默法则。在我们开始使用规则之前，我们需要学习一些新的定义和符号。

计算$2×2$矩阵的行列式

如果矩阵的行数和列数相同，我们称之为方矩阵。每个方矩阵都有一个与之相关的实数，称为其行列式。要找到方矩阵的行列式$\left[ \begin{matrix} a &b \\ c&d \end{matrix} \right] $，我们首先将其写为$\left| \begin{matrix} a &b \\ c&d \end{matrix} \right| $。为了获得决定值的实数值，我们减去对角线的乘积，如图所示。

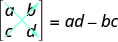
$显示 A 2 x 2 行列式，其第一行是 a, b，第二行是 c, d。这些值写在两条垂直线之间，而不是像矩阵那样写在方括号之间。显示了两个箭头，一个从 a 到 d，另一个从 c 到 b。这个行列式等于 ad 减去 bc。$

行列式

任何方矩阵（其中 a$\left[ \begin{matrix} a &b \\ c&d \end{matrix} \right] $、b、c 和 d 是实数）的行列式为

\[\left| \begin{matrix} a &b \\ c&d \end{matrix} \right| =ad−bc \nonumber \]

示例$\PageIndex{1}$

评估 ⓐ$\left[ \begin{matrix} 4 &-2 \\ 3&-1 \end{matrix} \right] $ ⓑ 的确定值$\left[ \begin{matrix} -3 &-4 \\ -2&0 \end{matrix} \right] $。

回答

ⓐ

	$。$
写下行列式。	$。$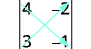
减去对角线的乘积。	$。$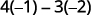
简化。	$。$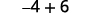
简化。	$。$

ⓑ

	$。$
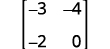
写下行列式。	$。$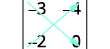
减去对角线的乘积。	$。$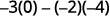
简化。	$。$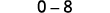
简化。	$。$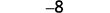

示例$\PageIndex{2}$

评估 ⓐ$\left[ \begin{matrix} 5&−3\\2&−4 \end{matrix} \right] $ ⓑ 的确定值$\left[ \begin{matrix} −4&−6\\0&7 \end{matrix} \right] $。

回答: ⓐ$−14$; ⓑ$−28$

示例$\PageIndex{3}$

评估 ⓐ$\left[ \begin{matrix} −1&3\\−2&4 \end{matrix} \right] $ ⓑ 的确定值$\left[ \begin{matrix} −7&−3\\−5&0 \end{matrix} \right] $。

回答: ⓐ 2 ⓑ$−15$

计算$3×3$矩阵的行列式

要评估$3×3$矩阵的行列式，我们必须能够评估行列式中条目的次要值。条目的次要项是通过删除包含$2×2$该条目的行列式中的行列式中的行列$3×3$式中得出的行列式。

入境未成年人$3×3$ A DETERMINANT

行列$3×3$式中条目的次要项是通过删除包含$2×2$该条目的行列式中的行列式中的行列$3×3$式中得出的行列式。

为了找到次要条目$a_1$，我们删除了包含它的行和列。因此，我们删除了第一行和第一列。然后我们写出剩下的行$2×2$列式。

$三乘三行列式的第一行是 a1、b1、c1。第 2 行是 a2、b2、c2。第 3 行是 a3、b3、c3。a1 突出显示。线条会删除第一行和第一列。剩下的被称为 a1 的未成年人。它显示为一个单独的行列式，其第一行是 b2，c2，第二行是 b3，c3。$

为了找到条目的次要项$b_2$，我们删除了包含它的行和列。因此，我们删除了$2^{nd}$行和$2^{nd}$列。然后我们写出剩下的行$2×2$列式。

$三乘三行列式的第一行是 a1、b1、c1。第 2 行是 a2、b2、c2。第 3 行是 a3、b3、c3。b2 突出显示。线条会删除第二行和第二列。剩下的是b2的次要内容。它被写成一个单独的行列式，其第一行是 a1，c1，第二行是 a3，c3。$

示例$\PageIndex{4}$

对于行列式$\left| \begin{matrix} 4&−2&3\\1&0&−3\\−2&−4&2 \end{matrix} \right|$，找到并计算 ⓐ$a_1$ ⓑ$b_3$ ⓒ 的次要值$c_2$。

回答

ⓐ

	$。$
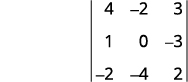
删除包含的行和列$a_1$。	$。$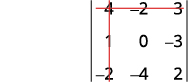
写下$2×2$剩下的行列式。	$。$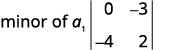
评估。	$。$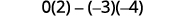
简化。	$。$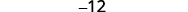

ⓑ

删除包含的行和列$b_3$。	$。$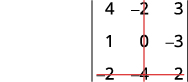
写下$2×2$剩下的行列式。	$。$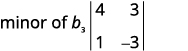
评估。	$。$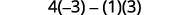
简化。	$。$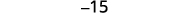

ⓒ

	$。$
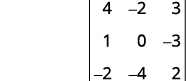
删除包含的行和列$c_2$。	$。$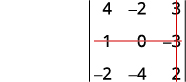
写下$2×2$剩下的行列式。	$。$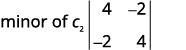
评估。	$。$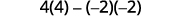
简化。	$。$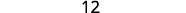

示例$\PageIndex{5}$

对于行列式$\left| \begin{matrix} 1&−1&4\\0&2&−1\\−2&−3&3 \end{matrix} \right|$，找到并计算 ⓐ$a_1$ ⓑ$b_2$ ⓒ 的次要值$c_3$。

回答: ⓐ 3 ⓑ 11 ⓒ 2

示例$\PageIndex{6}$

对于行列式$\left| \begin{matrix} −2&−1&0\\3&0&−1\\−1&−2&3 \end{matrix} \right|$，找到并计算 ⓐ$a_2$ ⓑ$b_3$ ⓒ 的次要值$c_2$。

回答: ⓐ$−3$ ⓑ 2 ⓒ 3

我们现在可以评估决定$3×3$因素了。为此，我们扩大了未成年人的范围，这使我们能够使用$3×3$决定因素来评估$2×2$决定因素，我们已经知道如何评估这些决定因素！

要通过沿第一行按未成年人扩展来评估行列式，我们使用以下模式：$3×3$

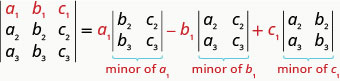
$3 x 3 行列式等于 a1 乘以 a1 的次要值减去 b1 的 b1 乘以 b1 的次要数加上 c1 乘以 c1 的次要值。$

请记住，要找到条目的次要项，我们会删除包含该条目的行和列。

由未成年人沿着第一排进行扩展，以评估$3×3$ DETERMINANT

要通过沿第一行按未成年人扩展来评估行列式，请采用以下模式：$3×3$

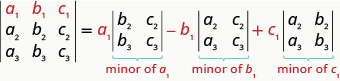
$3 x 3 行列式等于 a1 乘以 a1 的次要值减去 b1 的 b1 乘以 b1 的次要数加上 c1 乘以 c1 的次要值。$

示例$\PageIndex{7}$

通过沿第一行$\left| \begin{matrix} 2&−3&−1\\3&2&0\\−1&−1&−2 \end{matrix} \right|$按未成年人扩展来评估决定因素。

回答

	$。$
由第一排的未成年人扩展	$。$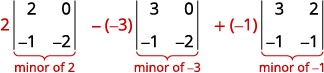
评估每个行列式。	$。$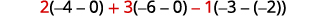
简化。	$。$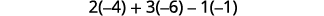
简化。	$。$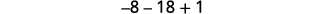
简化。	$。$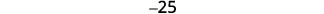

示例$\PageIndex{8}$

通过沿第一行$\left| \begin{matrix} 3&−2&4\\0&−1&−2\\2&3&−1 \end{matrix} \right|$按未成年人扩展来评估决定因素。

回答: 37

示例$\PageIndex{9}$

通过沿第一行$\left| \begin{matrix} 3&−2&−2\\2&−1&4\\−1&0&−3 \end{matrix} \right|$按未成年人扩展来评估决定因素。

回答: 7

为了评估行列$3×3$式，我们可以使用任何行或列按未成年人进行扩展。选择第一行以外的行或列有时会使工作变得更容易。

当我们按任何行或列展开时，我们必须注意扩展中术语的符号。为了确定术语的符号，我们使用以下符号模式图。

\[\left| \begin{matrix} +&−&+\\−&+&−\\+&−&+ \end{matrix} \right|\nonumber\]

标志图案

当未成年人使用行或列进行扩展时，扩展中的术语符号遵循以下模式。 \[\left| \begin{matrix} +&−&+\\−&+&−\\+&−&+ \end{matrix} \right|\nonumber\]

请注意，第一行中的符号模式与第一行扩展中术语之间的符号相匹配。

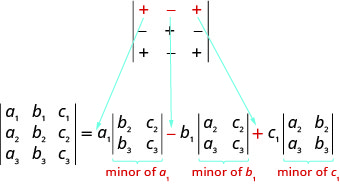
$三乘三行列式有第 1 行：加号、减号、加号、第 2 行：减号、加号、减号和第 3 行：加号、减号、加号。第一行中的三个符号分别指向 3 乘以 3 行列式展开中的次要行列式。加号指向 a1 的小调，减去 b1 的次要值，加上指向 c1 的次要值。$

既然我们可以按任何行或列进行扩展，那么我们如何决定使用哪一行或哪一列？通常，我们会尝试选择一行或一列，这样可以简化我们的计算。如果行列式包含 0，则使用包含 0 的行或列将使计算更容易。

示例$\PageIndex{10}$

通过未成年人扩张$\left| \begin{matrix} 4&−1&−3\\3&0&2\\5&−4&−3 \end{matrix} \right|$来评估决定因素。

回答

为了按未成年人进行扩展，我们会寻找可以简化计算的行或列。由于 0 在第二行和第二列中，因此按其中任何一个进行扩展都是不错的选择。由于第二行的负数少于第二列，我们将按第二行扩展。

	$。$
使用第二行进行扩展。
小心这些标志。	$。$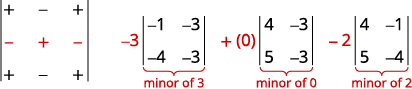
评估每个行列式。	$。$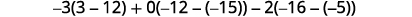
简化。	$。$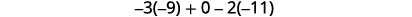
简化。	$。$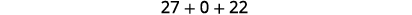
添加。	$。$

示例$\PageIndex{11}$

通过未成年人扩张$\left| \begin{matrix} 2&−1&−3\\0&3&−4\\3&−4&−3 \end{matrix} \right|$来评估决定因素。

回答: $−11$

示例$\PageIndex{12}$

通过未成年人扩张$\left| \begin{matrix} −2&−1&−3\\−1&2&2\\4&−4&0 \end{matrix} \right|$来评估决定因素。

回答: 8

使用克莱默法则求解方程组

克莱默法则是一种使用行列式求解方程组的方法。它可以通过用消法求解方程组的一般形式来得出。在这里，我们将演示具有两个变量的两个方程组和具有三个变量的三个方程组的规则。

让我们从两个方程组和两个变量开始。

克莱默求解两个方程组的法则

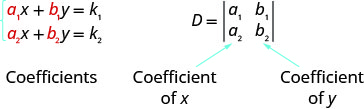
对于方程组$\left\{\begin{array} {l} a_1x+b_1y=k_1 \\ a_2x+b_2y=k_2\end{array}\right.$，解$(x,y)$可以通过以下方式确定

$x 是 D 上的 Dx，y 是 D 上的 Dy，其中 D 是行列式，第 1 行：a1、b1 和第 2 行 a2、b2 使用变量的系数；Dx 是行列式，第 1 行：k1、b1 和行 2：k2、b2，将 x 系数替换为辅音；Dy 是行列式，第 1 行：a1、k1 和第 2 行：a2、k2，替换 y带常量的系数$

请注意，为了形成行列式 D，我们使用变量的取系数。

$方程为 a1x 加 b1y 等于 k1，a2x 加 b2y 等于 k2。在这里，a1、a2、b1、b2 是系数。行列式是 D，第 1 行：a1、b1 和第 2 行：a2、b2。列 1 的系数为 x，列 2 的系数为$

请注意，为了形成行列式$D_x$和$D_y$，我们用常量代替我们正在寻找的变量的系数。

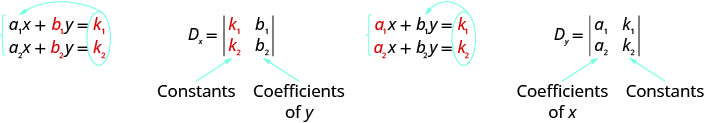
$方程为 a1x 加 b1y 等于 k1，a2x 加 b2y 等于 k2。在这里，a1、a2、b1、b2 是系数。行列式是 Dx 有第 1 行：k1、b1 和第 2 行：k2、b2。这里的第 1 列和第 2 列分别是 y 的常数和系数。行列式 Dy 有第 1 行：a1、k1 和第 2 行：a2、k2。在这里，第 1 列和第 2 列分别是 x 和常量的系数。$

示例$\PageIndex{13}$: How to Solve a System of Equations Using Cramer’s Rule

使用克莱默法则求解：$\left\{ \begin{array} {l} 2x+y=−4\\3x−2y=−6\end{array}\right.$

回答: $方程为 2x 加 y 等于减去 4 和 3x 减 2y 等于负 6。第 1 步。使用变量的系数计算行列式 D。行列式 D 的第 1 行：2、1 和行 2:3 减去 2。所以，D 等于减去 7。$ $第 2 步。计算行列式 Dx。使用常量代替 x 系数。我们将 x、2 和 3 的系数替换为负数 4 和负 6。我们得到 Dx 等于 14。$ $第 3 步。计算行列式 Dy。使用常量代替 y 系数。我们将 y、1 和 2 的系数替换为负数 4 和负 6。我们得到 Dy 等于 0。$ $第 4 步。找出 x 和 y。将方程中 D、Dx 和 Dy 的值替换为 D 上的 Dx，y 等于 D 上的 Dy，我们得到 x 等于负 2，y 等于 0。$ $第 5 步。将解写为有序对减去 2, 0。$ $第 6 步。检查有序对是否是两个原始方程的解。$

示例$\PageIndex{14}$

使用克莱默法则求解：$\left\{\begin{array} {l} 3x+y=−3 \\ 2x+3y=6 \end{array} \right.$

回答: $(−\frac{15}{7},\frac{24}{7})$

示例$\PageIndex{15}$

使用克莱默法则求解：$\left\{\begin{array} {l} −x+y=2\\2x+y=−4 \end{array} \right.$

回答: $(−2,0)$

使用克莱默法则求解由两个方程组成的系统。

使用变量的系数计算行列式 D。
评估行列式$D_x$。使用常量代替 x 系数。
评估行列式$D_y$。使用常量代替 y 系数。
找到 x 和 y。 $x=\frac{D_x}{D}$，$y=\frac{D_y}{D}$
将解写成有序对。
检查有序对是否是两个原始方程的解。

要使用克莱默法则求解由三个变量组成的三个方程组，我们基本上是按照两个方程组所做的那样。但是，我们现在必须求解三个变量才能得到解。决定因素也将$3×3$使我们的工作变得更加有趣！

克莱默求解三个方程组的法则

对于方程组$\left\{\begin{array} {l} a_1x+b_1y+c_1z=k_1\\a_2x+b_2y+c_2z=k_2\\a_3x+b_3y+c_3z=k_3\end{array}\right.$，解$(x,y,z)$可以通过以下方式确定

$x 是 D 上的 Dx，y 是 D 上的 Dy，z 是 D 上的 Dz，其中 D 是行列式，第 1 行：a1、b1、c1、第 2 行：a2、b2、c2、第 3 行：a3、b3、c3，使用变量的系数；Dx 是行列式，第 1 行：k2、b2、c2 和 rwo 3: k3、b3、c3，将 x 系数替换为辅音；Dy 是第 1 行的行列式：a1、k1、c1、第 2 行：a2、k2、c2 和第 3 行：a3、k3、c3，将 y 系数替换为常量；Dz 是行列式，第 1 行：a1、b1、k1；行 2：a2、b2、k2、第 3 行：a3、b3、k3；将 z 系数替换为常量。$

示例$\PageIndex{16}$

使用克莱默法则求解方程组：$\left\{\begin{array} {l} 3x−5y+4z=5\\5x+2y+z=0\\2x+3y−2z=3 \end{array} \right.$

回答

计算行列式 D。	$。$
使用第 1 栏按未成年人扩展。
$。$	$。$
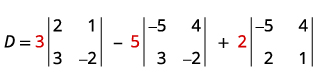
评估决定因素。	$。$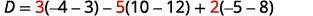
简化。	$。$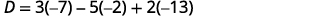
简化。	$。$
简化。	$。$
评估行列式$D_x$。使用常量替换 x 的系数。	$。$
使用第 1 栏按未成年人扩展。	$。$
评估决定因素。	$。$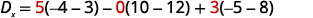
简化。	$。$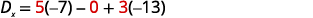
简化。	$。$
评估行列式 Dy.Dy。使用常量替换 y 的系数。	$。$
$。$	$。$
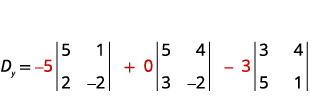
评估决定因素。	$。$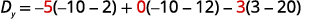
简化。	$。$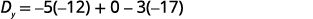
简化。	$。$
简化。	$。$
计算行列式 Dz.Dz。使用常量替换 z 的系数。	$。$
$。$	$。$
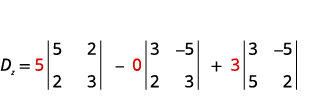
评估决定因素。	$。$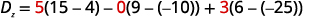
简化。	$。$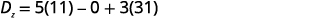
简化。	$。$
简化。	$。$
找到 x、y 和 z。	$。$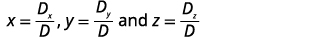
在值中替换。	$。$
简化。	$。$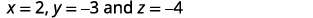
将解写为有序三元组。	$。$
检查有序三元组是否是所有三个原始方程的解。	我们把支票留给你。
	解决办法是$(2,−3,−4)$。

示例$\PageIndex{17}$

使用克莱默法则求解方程组：$\left\{\begin{array} {l} 3x+8y+2z=−5\\2x+5y−3z=0\\x+2y−2z=−1 \end{array} \right.$

回答: $(−9,3,−1)$

示例$\PageIndex{18}$

使用克莱默法则求解方程组：$\left\{\begin{array} {l} 3x+y−6z=−3\\2x+6y+3z=0\\3x+2y−3z=−6 \end{array} \right.$

回答: $(−6,3,−2)$

当 D 行列式的值为 0 时，克莱默的规则不起作用，因为这意味着我们将除以 0。但是何时$D=0$，系统要么不一致，要么相互依赖。

当 an d$D=0$$D_x,\space D_y$ 和 D 的值全部为零时，系统是一致且相互依存的，解无限多。

当 and$D=0$$D_x,\space D_y$ 和的值$D_z$不全部为零时，系统不一致且没有解决方案。

依赖和不一致的方程组

对于任何方程组，其中行列式$D=0$的值

\[ \begin{array} {lll} \textbf{Value of determinants} &\textbf{Type of system} &\textbf{Solution} \\ {D=0\text{ and }D_x,\space D_y\text{ and }D_z\text{ are all zero}} &\text{consistent and dependent} &\text{infinitely many solutions} \\ {D=0\text{ and }D_x,\space D_y\text{ and }D_z\text{ are not all zero}} &\text{inconsistent} &\text{no solution} \end{array} \nonumber\]

在下一个示例中，我们将使用行列式的值来找到系统的解。

示例$\PageIndex{19}$

使用克莱默法则求解方程组：$\left\{\begin{array} {l} x+3y=4\\−2x−6y=3 \end{array} \right.$

回答

$\begin{array} {ll} {} &{\left\{\begin{array} {l} x+3y=4\\−2x−6y=3 \end{array} \right.} \\ {\begin{array} {l} \text{Evaluate the determinantD,using the} \\ \text{coefficients of the variables.} \end{array}} &{D=\left|\begin{matrix} 1&3\\−2&−6\end{matrix}\right|} \\ {} &{D=−6−(−6)} \\ {} &{D=0} \end{array} $

我们无法使用克莱默法则来解决这个系统。但是，通过查看决定因素的值$D_x$$D_y$，我们可以确定系统是依赖的还是不一致的。

$\begin{array} {ll} {\text{Evaluate the determinant }D_x.} &{D_x=\left|\begin{matrix} 4&3\\3&−6\end{matrix}\right|} \\ {} &{D_x=−24−9} \\ {} &{D_x=15} \end{array} $

由于所有决定因素都不为零，因此系统不一致。没有解决办法。

示例$\PageIndex{20}$

使用克莱默法则求解方程组：$\left\{\begin{array} {l} 4x−3y=8\\8x−6y=14 \end{array} \right.$

回答: 没有解决办法

示例$\PageIndex{21}$

使用克莱默法则求解方程组：$\left\{\begin{array} {l} x=−3y+4\\2x+6y=8 \end{array} \right.$

回答: 无限的解决方案

使用决定因素求解应用程序

行列式的一个有趣的应用使我们能够测试点是否共线。三个点$(x_1,y_1)$，$(x_3,y_3)$当$(x_2,y_2)$且仅当下面的行列式为零时，和才是共线的。

\[\left|\begin{matrix}x_1&y_1&1\\x_2&y_2&1\\x_3&y_3&1\end{matrix}\right|=0\nonumber\]

检验共线点

三个点$(x_1,y_1)$，$(x_3,y_3)$当$(x_2,y_2)$且仅当

\[\left|\begin{matrix}x_1&y_1&1\\x_2&y_2&1\\x_3&y_3&1\end{matrix}\right|=0\nonumber\]

我们将在下一个示例中使用此属性。

示例$\PageIndex{22}$

确定点$(5,−5)$$(4,−3)$、和$(3,−1)$是否共线。

回答

	$。$
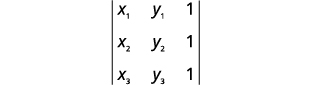
将这些值替换为行列式。 $(5,−5)$$(4,−3)$、和$(3,−1)$	$。$
使用第 3 列通过按未成年人扩展来评估行列式。	$。$
评估决定因素。	$。$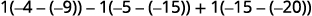
简化。	$。$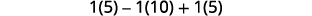
简化。	$。$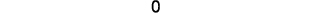
	确定值为 0，因此点是共线的。

示例$\PageIndex{23}$

确定点$(3,−2)$$(5,−3)$、和$(1,−1)$是否共线。

回答: 是的

示例$\PageIndex{24}$

确定点$(−4,−1)$$(−6,2)$、和$(−2,−4)$是否共线。

回答: 是的

访问这些在线资源，获取更多指导和练习，通过绘图求解线性不等式系统。

通过绘图求解线性不等式组
线性不等式系统

关键概念

行列式：任何方矩阵$\left[\begin{matrix}a&b\\c&d\end{matrix}\right]$的行列式为，其中 a、b、c 和 d 是实数
\[\left|\begin{matrix}a&b\\c&d\end{matrix}\right|=ad−bc\nonumber\]
由未成年人沿第一行扩展以评估一个 3×3 的行列式：要通过按未成年人沿第一行扩展来评估行列式，模式如下：$3×3$
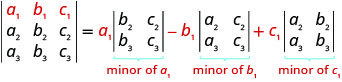
$3 x 3 行列式等于 a1 乘以 a1 的次要值减去 b1 的 b1 乘以 b1 的次要数加上 c1 乘以 c1 的次要值。$
符号模式：未成年人使用行或列进行扩展时，扩展中术语的符号遵循以下模式。
\[\left|\begin{matrix}+&−&+\\−&+&−\\+&−&+\end{matrix}\right|\nonumber\]
克莱默法则：对于方程组$\left\{\begin{array} {l} a_1x+b_1y=k_1\\a_2x+b_2y=k_2\end{array}\right.$，解$(x,y)$可以通过以下方式确定：要形成
$x 是 D 上的 Dx，y 是 D 上的 Dy，其中 D 是行列式，第 1 行：a1、b1 和第 2 行 a2、b2 使用变量的系数；Dx 是行列式，第 1 行：k1、b1 和行 2：k2、b2，将 x 系数替换为辅音；Dy 是行列式，第 1 行：a1、k1 和第 2 行：a2、k2，替换 y带常数的系数。$
行列式 D，我们使用变量的系数。
如何使用克莱默法则求解由两个方程组成的系统。
1. 使用变量的系数计算行列式 D。
2. 评估行列式$D_x$。使用常量代替 x 系数。
3. 评估行列式$D_y$。使用常量代替 y 系数。
4. 找到 x 和 y。 $x=\frac{D_x}{D}$，$y=\frac{D_y}{D}$。
5. 将解写成有序对。
6. 检查有序对是否是两个原始方程的解。
7. 依赖和不一致的方程组：对于任何方程组，其中行列$D=0$式的值\[ \begin{array} {lll} \textbf{Value of determinants} &\textbf{Type of system} &\textbf{Solution} \\ {D=0\text{ and }D_x,\space D_y\text{ and }D_z\text{ are all zero}} &\text{consistent and dependent} &\text{infinitely many solutions} \\ {D=0\text{ and }D_x,\space D_y\text{ and }D_z\text{ are not all zero}} &\text{inconsistent} &\text{no solution} \end{array} \nonumber\]
8. 共线点检验：当且仅当以下$(x_1,y_1)$条件$(x_2,y_2)$时，三个点、和才$(x_3,y_3)$是共线的
  \[\left|\begin{matrix}x_1&y_1&1\\x_2&y_2&1\\x_3&y_3&1\end{matrix}\right|=0\nonumber\]

词汇表

行列式: 每个方矩阵都有一个与之相关的实数，称为其行列式。

3×33×3 行列式中条目的次要项: 3×33×3 行列式中条目的次要项是通过消除包含该条目的 3×33×3 行列式中的行列式得出的 2×22×2 行列式。

方矩阵: 方矩阵是具有相同行数和列数的矩阵。

行列式

示例\(\PageIndex{1}\)

示例\(\PageIndex{2}\)

示例\(\PageIndex{3}\)

入境未成年人\(3×3\) A DETERMINANT

示例\(\PageIndex{4}\)

示例\(\PageIndex{5}\)

示例\(\PageIndex{6}\)

由未成年人沿着第一排进行扩展，以评估\(3×3\) DETERMINANT

示例\(\PageIndex{7}\)

示例\(\PageIndex{8}\)

示例\(\PageIndex{9}\)

标志图案

示例\(\PageIndex{10}\)

示例\(\PageIndex{11}\)

示例\(\PageIndex{12}\)