4.6: 使用矩阵求解方程组

学习目标

在本节结束时，您将能够：

• 为方程组编写增强矩阵
• 在矩阵上使用行运算
• 使用矩阵求解方程组

在开始之前，请参加这个准备测验。

1. 解决：$3(x+2)+4=4(2x−1)+9$。
   如果你错过了这个问题，请查看 [链接]。
2. 解决：$0.25p+0.25(x+4)=5.20$。
   如果你错过了这个问题，请查看 [链接]。
3. 评估何时$x=−2$和$y=3:2x^2−xy+3y^2$。
   如果你错过了这个问题，请查看 [链接]。

为方程组编写增强矩阵

求解方程组可能是一项繁琐的操作，其中一个简单的错误可能会对求解造成严重破坏。 还有一种替代方法，它使用基本的排除程序，但使用更简单的符号。 该方法涉及使用矩阵。 矩阵是按行和列排列的矩形数字数组。

矩阵

矩阵是按行和列排列的矩形数字数组。

包含 m 行和 n 列的矩阵具有顺序$m\times n$。 下面左边的矩阵有 2 行和 3 列，所以它有顺序$2\times 3$。 我们说它是一个 2 x 3 的矩阵。

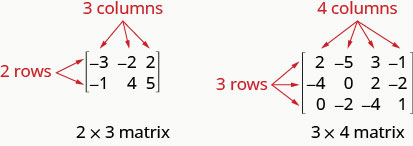
矩阵中的每个数字都称为矩阵中的元素或条目。

我们将使用矩阵来表示线性方程组。 我们用标准形式写每个方程，变量的系数和每个方程的常数在矩阵中变成一行。 然后，每列将是系统中其中一个变量的系数或常量。 垂直线取代等号。 我们将生成的矩阵称为方程组的增强矩阵。

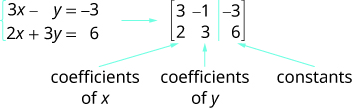
请注意，第一列由 x 的所有系数组成，第二列是 y 的所有系数，第三列是所有常量。

示例$\PageIndex{1}$

ⓐ$\left\{ \begin{array} {l} 5x−3y=−1 \\ y=2x−2 \end{array} \right.$ ⓑ$\left\{ \begin{array} {l} 6x−5y+2z=3 \\ 2x+y−4z=5 \\ 3x−3y+z=−1 \end{array} \right.$

回答

ⓐ 第二个方程不是标准形式。 我们用标准形式重写第二个方程。

$$\begin{aligned} y=2x−2 \\ −2x+y=−2 \end{aligned} \nonumber$$

我们将第二个方程替换为其标准形式。 在增强矩阵中，第一个方程给我们第一行，第二个方程给我们第二行。 垂直线取代等号。

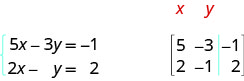
ⓑ 所有三个方程均为标准形式。 在增强矩阵中，第一个方程给我们第一行，第二个方程给我们第二行，第三个方程给我们第三行。 垂直线取代等号。

示例$\PageIndex{2}$

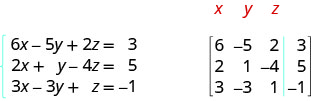
将每个线性方程组写成增强矩阵：

ⓐ$\left\{ \begin{array} {l} 3x+8y=−3 \\ 2x=−5y−3 \end{array} \right.$ ⓑ$\left\{ \begin{array} {l} 2x−5y+3z=8 \\ 3x−y+4z=7 \\ x+3y+2z=−3 \end{array} \right.$

回答

ⓐ$\left[ \begin{matrix} 3 &8 &-3 \\ 2 &5 &−3 \end{matrix} \right]$

ⓑ$\left[ \begin{matrix} 2 &3 &1 &−5 \\ −1 &3 &3 &4 \\ 2 &8 &7 &−3 \end{matrix} \right]$

示例$\PageIndex{3}$

将每个线性方程组写成增强矩阵：

ⓐ$\left\{ \begin{array} {l} 11x=−9y−5 \\ 7x+5y=−1 \end{array} \right.$ ⓑ$\left\{ \begin{array} {l} 5x−3y+2z=−5 \\ 2x−y−z=4 \\ 3x−2y+2z=−7 \end{array} \right.$

回答

ⓐ$\left[ \begin{matrix} 11 &9 &−5 \\ 7 &5 &−1 \end{matrix} \right]$
ⓑ$\left[ \begin{matrix} 5 &−3 &2 &−5 \\ 2 &−1 &−1 &4 \\ 3 &−2 &2 &−7 \end{matrix} \right]$

这很重要，因为我们使用矩阵求解方程组，以便能够在方程组和矩阵之间来回移动。 下一个例子要求我们获取矩阵中的信息并写出方程组。

示例$\PageIndex{4}$

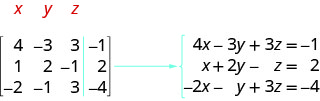
写出与增强矩阵对应的方程组：

$\left[ \begin{array} {ccc|c} 4 &−3 &3 &−1 \\ 1 &2 &−1 &2 \\ −2 &−1 &3 &−4 \end{array} \right]$。

回答

我们记得每行对应一个方程，每个条目都是变量或常量的系数。 垂直线取代等号。 由于这个矩阵是 a$4\times 3$，我们知道它将转化为由三个变量组成的三个方程组。

示例$\PageIndex{5}$

写出与增强矩阵对应的方程组:$\left[ \begin{matrix} 1 &−1 &2 &3 \\ 2 &1 &−2 &1 \\ 4 &−1 &2 &0 \end{matrix} \right]$.

回答

$\left\{ \begin{array} {l} x−y+2z=3 \\ 2x+y−2z=1 \\ 4x−y+2z=0 \end{array} \right.$

示例$\PageIndex{6}$

写出与增强矩阵对应的方程组:$\left[ \begin{matrix} 1 &1 &1 &4 \\ 2 &3 &−1 &8 \\ 1 &1 &−1 &3 \end{matrix} \right]$.

回答

$\left\{ \begin{array} {l} x+y+z=4 \\ 2x+3y−z=8 \\ x+y−z=3 \end{array} \right.$

在矩阵上使用行运算

一旦方程组采用增强矩阵形式，我们将对行执行运算，从而得出解。

要通过消除求解，我们在方程组中按哪个顺序排列方程都没关系。 同样，在矩阵中我们可以交换行。

当我们通过消除求解时，我们经常将其中一个方程乘以一个常数。 由于每行代表一个方程，我们可以将方程的每一边乘以一个常数，同样，我们可以将行中的每个条目乘以除 0 之外的任何实数。

在消除中，我们经常将一行的倍数添加到另一行。 在矩阵中，我们可以将一行及其总和替换为另一行的倍数。

这些操作称为行运算，将帮助我们使用矩阵求解方程组。

行操作

在矩阵中，可以在任何行上执行以下操作，生成的矩阵将等同于原始矩阵。

1. 将任意两行互换。
2. 将一行乘以 0 以外的任意实数。
3. 将一行的非零倍数添加到另一行。

执行这些操作很容易，但是所有的算术都可能导致错误。 如果我们使用系统记录每个步骤中的行操作，则回去检查我们的工作要容易得多。

我们使用带下标的大写字母来表示每一行。 然后，我们在新矩阵的左侧显示运算。 要显示互换行，请执行以下操作：

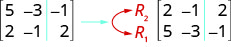
要将第 2 行乘以$−3$：

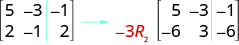
要将第 2 行乘以$−3$并将其添加到第 1 行，请执行以下操作：

示例$\PageIndex{7}$

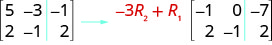
在增强矩阵上执行指示的操作：

ⓐ 交换第 2 行和第 3 行。

ⓑ 将第 2 行乘以 5。

ⓒ 将第 3 行乘以 −2−2，然后与第 1 行相加。

$\left[ \begin{array} {ccc|c} 6 &−5 &2 &3 \\ 2 &1 &−4 &5 \\ 3 &−3 &1 &−1 \end{array} \right]$

回答

ⓐ 我们交换第 2 行和第 3 行。

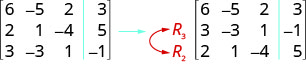
ⓑ 我们将第 2 行乘以 5。

ⓒ 我们将第 3 行乘以，$−2$然后相加到第 1 行。

示例$\PageIndex{8}$

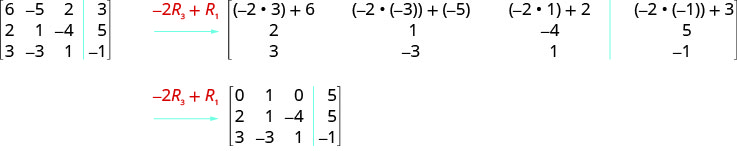
在增强矩阵上执行指示的操作：

ⓐ 交换第 1 行和第 3 行。

ⓑ 将第 3 行乘以 3。

ⓒ 将第 3 行乘以 2 并加到第 2 行。

$\left[ \begin{array} {ccc|c} 5 &−2 &-2 &-2 \\ 4 &-1 &−4 &4 \\ -2 &3 &0 &−1 \end{array} \right]$

回答

ⓐ$\left[ \begin{matrix} −2 &3 &0 &−2 \\ 4 &−1 &−4 &4 \\ 5 &−2 &−2 &−2 \end{matrix} \right]$

ⓑ$\left[ \begin{matrix} −2 &3 &0 &−2 \\ 4 &−1 &−4 &4 \\ 15 &−6 &−6 &−6 \end{matrix} \right]$

ⓒ$\left[ \begin{matrix} -2 &3 &0 &2 & \\ 3 &4 &-13 &-16 &-8 \\ 15 &-6 &-6 &-6 & \end{matrix} \right]$

示例$\PageIndex{9}$

在增强矩阵上执行指示的操作：

ⓐ 互换第 1 行和第 2 排

ⓑ 将第 1 行乘以 2

ⓒ 将第 2 行乘以 3 并相加到第 1 行。

$\left[ \begin{array} {ccc|c} 2 &−3 &−2 &−4 \\ 4 &1 &−3 &2 \\ 5 &0 &4 &−1 \end{array} \right]$

回答

ⓐ$\left[ \begin{matrix} 4 &1 &−3 &2 \\ 2 &−3 &−2 &−4 \\ 5 &0 &4 &−1 \end{matrix} \right]$
ⓑ$\left[ \begin{matrix} 8 &2 &−6 &4 \\ 2 &−3 &−2 &−4 \\ 5 &0 &4 &−1 \end{matrix} \right]$
ⓒ$\left[ \begin{matrix} 14 &−7 &−12 &−8 \\ 2 &−3 &−2 &−4 \\ 5 &0 &4 &−1 \end{matrix} \right]$

既然我们已经练习了行运算，我们将看一个增强矩阵，弄清楚我们将使用什么运算来实现目标。 这正是我们在淘汰时所做的。 我们决定将一行乘以哪个数字，以便在将各行相加时消除变量。

有了这个系统，你会怎么做才能消除 x？

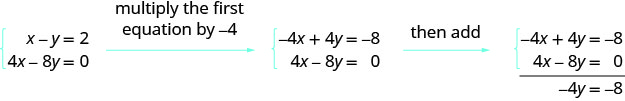
下一个例子本质上做了同样的事情，只是对矩阵做了同样的事情。

示例$\PageIndex{10}$

执行所需的行运算，使第 2 行中的第一个条目在增强矩阵中为零：$\left[ \begin{array} {cc|c} 1 &−1 &2 \\ 4 &−8 &0 \end{array} \right]$

回答

要将 4 设为 0，我们可以将第 1 行乘以，$−4$然后将其添加到第 2 行。

示例$\PageIndex{11}$

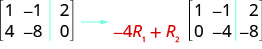
执行所需的行运算，使第 2 行中的第一个条目在增强矩阵中为零：$\left[ \begin{array} {cc|c} 1 &−1 &2 \\ 3 &−6 &2 \end{array} \right]$

回答

$\left[ \begin{matrix} 1 &−1 &2 \\ 0 &−3 &−4 \end{matrix} \right]$

示例$\PageIndex{12}$

执行所需的行运算，使第 2 行中的第一个条目在增强矩阵中为零：$\left[ \begin{array} {cc|c} 1 &−1 &3 \\ -2 &−3 &2 \end{array} \right]$

回答

$\left[ \begin{matrix} 1 &−1 &3 \\ 0 &−5 &8 \end{matrix} \right]$

使用矩阵求解方程组

为了使用矩阵求解方程组，我们使用行运算将增强矩阵转换为行梯队形式的矩阵。 对于一致且独立的方程组，其增强矩阵为行梯队形式，垂直线左侧，对角线上的每个条目均为 1，对角线下方的所有条目均为零。

行梯队表单

对于一致且独立的方程组，其增强矩阵为行梯队形式，垂直线左侧，对角线上的每个条目均为 1，对角线下方的所有条目均为零。

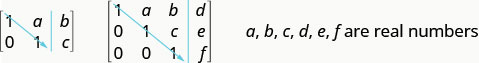
一旦我们将增强矩阵变成行梯队形式，我们就可以写出等效的方程组并读取至少一个变量的值。 然后，我们在另一个方程中替换这个值以继续求解其他变量。 下一个示例说明了这个过程。

如何使用矩阵求解方程组

使用矩阵求解方程组：$\left\{ \begin{array} {l} 3x+4y=5 \\ x+2y=1 \end{array} \right.$

回答

示例$\PageIndex{14}$

使用矩阵求解方程组：$\left\{ \begin{array} {l} 2x+y=7 \\ x−2y=6 \end{array} \right.$

回答

解决方案是$(4,−1)$。

示例$\PageIndex{15}$

使用矩阵求解方程组：$\left\{ \begin{array} {l} 2x+y=−4 \\ x−y=−2 \end{array} \right.$

回答

解决方案是$(−2,0)$。

此处总结了这些步骤。

使用矩阵求解方程组。

1. 为方程组写出增强矩阵。
2. 使用行操作将第 1 行、列 1 中的条目变为 1。
3. 使用行运算，在 1 下方的第 1 列中取零。
4. 使用行运算，将第 2 行、第 2 列中的条目变为 1。
5. 继续该过程，直到矩阵呈行梯队形式。
6. 写出相应的方程组。
7. 使用替换来查找其余变量。
8. 将解写成有序对或三组。
9. 检查解是否使原始方程式成立。

这是一个视觉效果，显示了将 1 和 0 置于行梯队形态的正确位置的顺序。

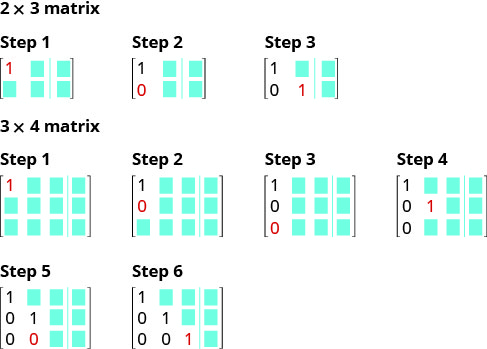
当方程组有三个方程时，我们使用相同的程序。

示例$\PageIndex{16}$

使用矩阵求解方程组：$\left\{ \begin{array} {l} 3x+8y+2z=−5 \\ 2x+5y−3z=0 \\ x+2y−2z=−1 \end{array} \right.$

回答

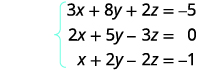
为方程写出增强矩阵。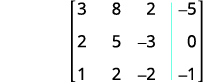
将第 1 行和第 3 行交换为第 1 行中的条目，第 1 列中的条目为 1。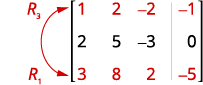
使用行运算，在 1 下方的第 1 列中取零。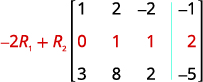
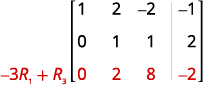
第 2 行第 2 列中的条目现在是 1。
继续该过程，直到矩阵 呈行梯队形式。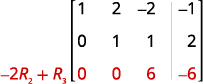
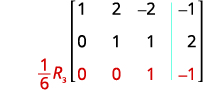
矩阵现在是行梯队形式。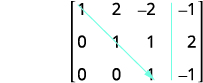
写出相应的方程组。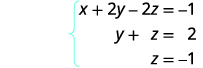
使用替换来查找其余变量。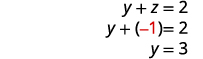
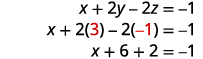
将解写成有序对或三组。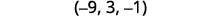
检查解是否使原始方程式成立。	我们把支票留给你。

示例$\PageIndex{17}$

使用矩阵求解方程组：$\left\{ \begin{array} {l} 2x−5y+3z=8 \\ 3x−y+4z=7 \\ x+3y+2z=−3 \end{array} \right.$

回答

$(6,−1,−3)$

示例$\PageIndex{18}$

使用矩阵求解方程组：$\left\{ \begin{array} {l} −3x+y+z=−4 \\ −x+2y−2z=1 \\ 2x−y−z=−1 \end{array} \right.$

回答

$(5,7,4)$

到目前为止，我们对矩阵的研究只涉及一致和独立的系统，这意味着它们只有一个解决方案。 现在让我们来看看当我们对依赖或不一致的系统使用矩阵时会发生什么。

示例$\PageIndex{19}$

使用矩阵求解方程组：$\left\{ \begin{array} {l} x+y+3z=0 \\ x+3y+5z=0 \\ 2x+4z=1 \end{array} \right.$

回答

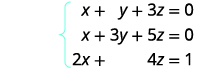
为方程写出增强矩阵。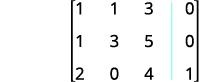
第 1 行第 1 列中的条目为 1。
使用行运算，在 1 下方的第 1 列中取零。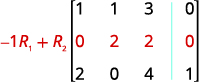
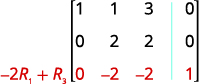
继续该过程，直到矩阵呈行梯队形式。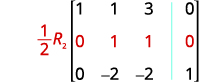
将第 2 行乘以 2 并将其添加到第 3 行。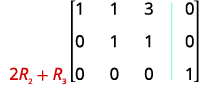
此时，我们在第 3 行的左侧全部为零。
写出相应的方程组。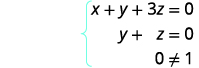
因为$0 \neq 1$我们有错误的陈述。 就像我们使用其他方法求解系统时一样，这告诉我们我们有一个不一致的系统。 没有解决办法。

示例$\PageIndex{20}$

使用矩阵求解方程组：$\left\{ \begin{array} {l} x−2y+2z=1 \\ −2x+y−z=2 \\ x−y+z=5 \end{array} \right.$

回答

没有解决办法

示例$\PageIndex{21}$

使用矩阵求解方程组：$\left\{ \begin{array} {l} 3x+4y−3z=−2 \\ −2x+3y−z=−1 \\ 2x+y−2z=6 \end{array} \right.$

回答

没有解决办法

最后一个系统不一致，因此没有解决方案。 下一个例子是依赖的，有无限多的解。

示例$\PageIndex{22}$

使用矩阵求解方程组：$\left\{ \begin{array} {l} x−2y+3z=1 \\ x+y−3z=7 \\ 3x−4y+5z=7 \end{array} \right.$

回答

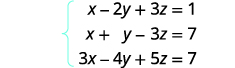
为方程写出增强矩阵。
第 1 行第 1 列中的条目为 1。
使用行运算，在 1 下方的第 1 列中取零。
继续该过程，直到矩阵呈行梯队形式。
将第 2 行乘以$−2$并将其添加到第 3 行。
此时，我们在底行中全部为零。
写出相应的方程组。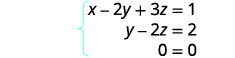
因为$0=0$我们有真实的陈述。 就像我们通过替换求解时一样，这告诉我们我们有一个依赖系统。 有无限多的解决方案。
在第二个方程中以 z 求解 y。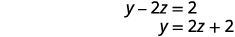
以 z 为单位求解 x 的第一个方程。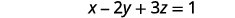
替代$y=2z+2$。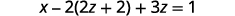
简化。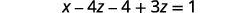
简化。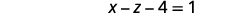
简化。
该系统有无限多的解$(x,y,z)$，其中$x=z+5;\space y=2z+2;\space z$是任何实数。

示例$\PageIndex{23}$

使用矩阵求解方程组：$\left\{ \begin{array} {l} x+y−z=0 \\ 2x+4y−2z=6 \\ 3x+6y−3z=9 \end{array} \right.$

回答

无限多的解$(x,y,z)$，其中$x=z−3;\space y=3;\space z$是任何实数。

示例$\PageIndex{24}$

使用矩阵求解方程组：$\left\{ \begin{array} {l} x−y−z=1 \\ −x+2y−3z=−4 \\ 3x−2y−7z=0 \end{array} \right.$

回答

无限多的解$(x,y,z)$，其中$x=5z−2;\space y=4z−3;\space z$是任何实数。

访问此在线资源，获取有关高斯消灭的更多指导和练习。

• 高斯消除

关键概念

• 矩阵：矩阵是按行和列排列的矩形数字数组。 包含 m 行和 n 列的矩阵具有顺序$m\times n$。 下面左边的矩阵有 2 行和 3 列，所以它有顺序$2\times 3$。 我们说它是一个 2 x 3 的矩阵。
  
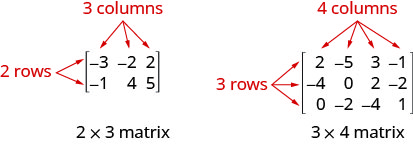
  矩阵中的每个数字都称为矩阵中的元素或条目。
• 行运算：在矩阵中，可以在任何行上执行以下操作，生成的矩阵将等同于原始矩阵。
  • 将任意两行互换
  • 将一行乘以 0 以外的任意实数
  • 将一行的非零倍数添加到另一行
• Row-Echelon Form：对于一致且独立的方程组，当垂直线左边、对角线上的每个条目都为 1 且对角线下方的所有条目均为零时，其增强矩阵为行梯队形式。
  
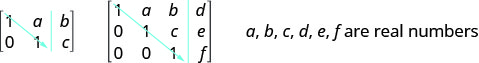
• 如何使用矩阵求解方程组。
  1. 为方程组写出增强矩阵。
  2. 使用行操作将第 1 行、列 1 中的条目变为 1。
  3. 使用行运算，在 1 下方的第 1 列中取零。
  4. 使用行运算，将第 2 行、第 2 列中的条目变为 1。
  5. 继续该过程，直到矩阵呈行梯队形式。
  6. 写出相应的方程组。
  7. 使用替换来查找其余变量。
  8. 将解写成有序对或三组。
  9. 检查解是否使原始方程式成立。

词汇表

矩阵

矩阵是按行和列排列的矩形数字数组。

行梯队表单

当垂直线左侧时，矩阵为行梯队形式，对角线上的每个条目均为 1，对角线下方的所有条目均为零。