4.5E：练习

Last updated
Save as PDF

Page ID: 203896

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

练习成就完美

确定有序三元组是否是具有三个变量的三个线性方程组的解

在以下练习中，确定订购的三元组是否是系统的解决方案。

1。 $\left\{ \begin{array} {l} 2x−6y+z=3 \\ 3x−4y−3z=2 \\ 2x+3y−2z=3 \end{array} \right. $

ⓐ$(3,1,3)$
ⓑ$(4,3,7)$

2。 $\left\{ \begin{array} {l} -3x+y+z=-4 \\ -x+2y-2z=1 \\ 2x-y-z=-1 \end{array} \right. $

ⓐ$(−5,−7,4)$
ⓑ$(5,7,4)$

回答: ⓐ 不 ⓑ 是的

3。 $\left\{ \begin{array} {l} y−10z=−8 \\ 2x−y=2 \\ x−5z=3 \end{array} \right. $

ⓐ$(7,12,2)$
ⓑ$(2,2,1)$

4。 $\left\{ \begin{array} {l} x+3y−z=1 \\ 5y=\frac{2}{3}x \\ −2x−3y+z=−2 \end{array} \right. $

ⓐ$(−6,5,12)$
ⓑ$(5,\frac{4}{3},−3)$

回答: ⓐ 不 ⓑ 是的

求解具有三个变量的线性方程组

在以下练习中，求解方程组。

5。 $\left\{ \begin{array} {l} 5x+2y+z=5 \\ −3x−y+2z=6 \\ 2x+3y−3z=5 \end{array} \right. $

6。 $\left\{ \begin{array} {l} 6x−5y+2z=3 \\ 2x+y−4z=5 \\ 3x−3y+z=−1 \end{array} \right. $

回答: $(4,5,2)$

7。 $\left\{ \begin{array} {l} 2x−5y+3z=8 \\ 3x−y+4z=7 \\ x+3y+2z=−3 \end{array} \right. $

8。 $\left\{ \begin{array} {l} 5x−3y+2z=−5 \\ 2x−y−z=4 \\ 3x−2y+2z=−7 \end{array} \right. $

回答: $(7,12,−2)$

9。 $\left\{ \begin{array} {l} 3x−5y+4z=5 \\ 5x+2y+z=0 \\ 2x+3y−2z=3 \end{array} \right. $

10。 $\left\{ \begin{array} {l} 4x−3y+z=7 \\ 2x−5y−4z=3 \\ 3x−2y−2z=−7 \end{array} \right. $

回答: $(−3,−5,4)$

11。 $\left\{ \begin{array} {l} 3x+8y+2z=−5 \\ 2x+5y−3z=0 \\ x+2y−2z=−1 \end{array} \right. $

12。 $\left\{ \begin{array} {l} 11x+9y+2z=−9 \\ 7x+5y+3z=−7 \\ 4x+3y+z=−3 \end{array} \right. $

回答: $(2,−3,−2)$

13。 $\left\{ \begin{array} {l} \frac{1}{3}x−y−z=1 \\ x+\frac{5}{2}y+z=−2 \\ 2x+2y+\frac{1}{2}z=−4 \end{array} \right. $

14。 $\left\{ \begin{array} {l} x+\frac{1}{2}y+\frac{1}{2}z=0 \\ \frac{1}{5}x−\frac{1}{5}y+z=0 \\ \frac{1}{3}x−\frac{1}{3}y+2z=−1 \end{array} \right. $

回答: $(6,−9,−3)$

15。 $\left\{ \begin{array} {l} x+\frac{1}{3}y−2z=−1 \\ \frac{1}{3}x+y+\frac{1}{2}z=0 \\ \frac{1}{2}x+\frac{1}{3}y−\frac{1}{2}z=−1 \end{array} \right. $

16。 $\left\{ \begin{array} {l} \frac{1}{3}x−y+\frac{1}{2}z=4 \\ \frac{2}{3}x+\frac{5}{2}y−4z=0 \\ x−\frac{1}{2}y+\frac{3}{2}z=2 \end{array} \right. $

回答: $(3,−4,−2)$

17。 $\left\{ \begin{array} {l} x+2z=0 \\ 4y+3z=−2 \\ 2x−5y=3 \end{array} \right. $

18。 $\left\{ \begin{array} {l} 2x+5y=4 \\ 3y−z=\frac{3}{4} \\ x+3z=−3 \end{array} \right. $

回答: $(−3,2,3)$

19。 $\left\{ \begin{array} {l} 2y+3z=−1 \\ 5x+3y=−6 \\ 7x+z=1 \end{array} \right. $

20。 $\left\{ \begin{array} {l} 3x−z=−3 \\ 5y+2z=−6 \\ 4x+3y=−8 \end{array} \right. $

回答: $(−2,0,−3)$

21。 $\left\{ \begin{array} {l} 4x−3y+2z=0 \\ −2x+3y−7z=1 \\ 2x−2y+3z=6 \end{array} \right. $

22。 $\left\{ \begin{array} {l} x−2y+2z=1 \\ −2x+y−z=2 \\ x−y+z=5 \end{array} \right. $

回答: 没有解决办法

23。 $\left\{ \begin{array} {l} 2x+3y+z=1 \\ 2x+y+z=9 \\ 3x+4y+2z=20 \end{array} \right. $

24。 $\left\{ \begin{array} {l} x+4y+z=−8 \\ 4x−y+3z=9 \\ 2x+7y+z=0 \end{array} \right. $

回答: $x=\frac{203}{16};\space y=–\frac{25}{16};\space z=–\frac{231}{16};$

25。 $\left\{ \begin{array} {l} x+2y+z=4 \\ x+y−2z=3 \\ −2x−3y+z=−7 \end{array} \right. $

26。 $\left\{ \begin{array} {l} x+y−2z=3 \\ −2x−3y+z=−7 \\ x+2y+z=4 \end{array} \right. $

回答: $(x,y,z)$哪里$x=5z+2;\space y=−3z+1;\space z$是任何实数

27。 $\left\{ \begin{array} {l} x+y−3z=−1 \\ y−z=0 \\ −x+2y=1 \end{array} \right. $

28。 $\left\{ \begin{array} {l} x−2y+3z=1 \\ x+y−3z=7 \\ 3x−4y+5z=7 \end{array} \right. $

回答: $(x,y,z)$哪里$x=5z−2;\space y=4z−3;\space z$是任何实数

使用具有三个变量的线性方程组求解应用程序

在以下练习中，解决给定的问题。

29。三角形角度的测量总和为 180。第二个和第三个角度的测量值之和是第一个角度测量值的两倍。第三个角度比第二个角度多十二。找出三个角度的测量值。

30。三角形角度的测量总和为 180。第二个和第三个角度的测量值之和是第一个角度测量值的三倍。第三个角度比第二个角度多十五。找出三个角度的测量值。

回答: 42、50、58

31。在剧院观看大型音乐剧后，顾客可以购买纪念品。如果一个家庭购买了 4 件 T 恤、视频和 1 只毛绒玩具，则总额为 135 美元。

一对夫妇为侄女买了 2 件 T 恤、视频和 3 只毛绒玩具，花了 115 美元。另一对夫妇购买了2件T恤、视频和1只毛绒玩具，总价为85美元。每件商品的成本是多少？

32。教会青年团体正在出售零食，以筹集资金参加他们的会议。艾米卖出了 2 磅糖果、3 盒饼干和 1 罐爆米花，总销售额为 65 美元。布莱恩卖出了 4 磅糖果、6 盒饼干和 3 罐爆米花，总销售额为 140 美元。宝琳娜售出了 8 磅糖果、8 盒饼干和 5 罐爆米花，总销售额为 250 美元。每件商品的成本是多少？

回答: 20 美元、5 美元、10 美元

写作练习

33。用你自己的话解释通过消除求解具有三个变量的线性方程组的步骤。

34。你怎么知道一个由三个变量组成的三个线性方程组何时没有解？无限多的解决方案？

回答: 答案会有所不同。

自检

ⓐ 完成练习后，使用这份清单来评估你对本节目标的掌握程度。

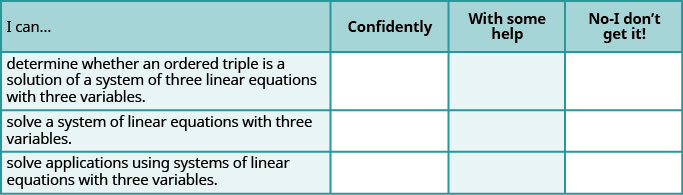
$此表有 4 列、3 行和一个标题行。标题行在一些帮助下自信地标记了我能做到的每一列，不，我不明白。第一行包含以下语句：确定有序三元组是否是具有三个变量的三个线性方程组的解，求解具有三个变量的线性方程组，使用具有三个变量的线性方程组求解应用程序。其余列为空白。$

ⓑ 在 1-10 的等级中，根据你在清单上的回复，你会如何评价你对本节的掌握程度？你怎么能改善这个？