Home
简体中文
中级代数 (OpenStax)
4: 线性方程组
4.5: 求解具有三个变量的方程组

4.5: 求解具有三个变量的方程组

Last updated
Save as PDF

Page ID: 203893

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

学习目标

在本节结束时，您将能够：

确定有序三元组是否是具有三个变量的三个线性方程组的解
求解具有三个变量的线性方程组
使用具有三个变量的线性方程组求解应用程序

在开始之前，请参加这个准备测验。

评估$5x−2y+3z$何时$x=−2, y=−4,$以及$z=3.$
是否错过了这个问题，请查看 [链接]。
将方程归类为条件方程、恒等方程或矛盾方程，然后陈述解。 $ \left\{ \begin{array} {l} −2x+y=−11 \\ x+3y=9 \end{array} \right. $
如果你错过了这个问题，请查看 [链接]。
将方程归类为条件方程、恒等方程或矛盾方程，然后陈述解。 $\left\{ \begin{array} {l} 7x+8y=4 \\ 3x−5y=27 \end{array} \right. $
如果你错过了这个问题，请查看 [链接]。

确定有序三元组是否是具有三个变量的三个线性方程组的解

在本节中，我们将扩展求解线性方程组的工作。到目前为止，我们已经使用了包含两个方程和两个变量的方程组。现在我们将使用三个方程组和三个变量。但是首先让我们回顾一下关于求解最多涉及两个变量的方程和方程组的知识。

我们之前了解到线性方程的图形是一条线。$ax+by=c$ 直线上的每个点都是有序对$(x,y)$，是方程的解。对于由两个变量组成的两个方程组，我们绘制两条线。然后我们可以看到，作为每个方程解的所有点都形成了一条直线。而且，通过找到这些线路的共同点，我们将找到系统的解决方案。

一个变量中的大多数线性方程都有一个解，但是我们看到有些方程称为矛盾，没有解，而对于其他称为恒等式的方程，所有数字都是解

我们知道，当我们求解一个由两个线性方程组成的系统时，由同一平面上的两条线形表示的线性方程组时，有三种可能的情况，如图所示。

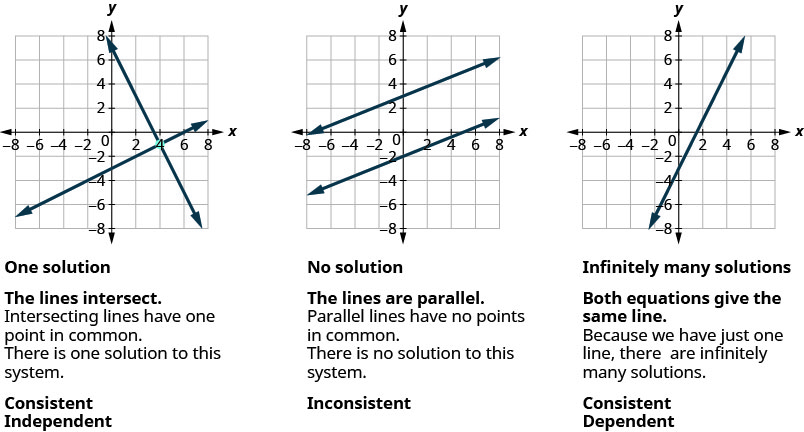
$图中显示了三张图表。在第一条中，两条线相交。相交线有一个共同点。这个系统有一个解决方案。该图标为 “一致独立”。在第二张图中，两条线是平行的。平行线没有共同点。这个系统没有解决办法。该图被标记为不一致。在第三张图中，只有一条线。两个方程给出相同的直线。因为我们只有一条线，所以有无限多的解决方案。它被标记为一致依赖关系。$

同样，对于具有三个变量 ax+by+cz=d、ax+by+cz=d 的线性方程，该方程的每个解都是一个有序三元组 (x, y, z) (x, y, z)，使方程成真。

三个变量中的线性方程

具有三个变量的线性方程的形式为：其中 a、b、 c 和 d 是实数，a、b 和 c 不全是 0

\[ ax+by+cz=d\nonumber \]

方程的每个解都是一个有序三元组，$(x,y,z)$这使得方程成真。

作为一个方程解的所有点在三维空间中形成一个平面。而且，通过找到飞机的共同点，我们将找到系统的解决方案。

当我们求解由空间中三个平面的图表示的三个线性方程组时，有三种可能的情况。

$图中显示了八个数字。第一个显示了三个相交的平面，其中一个共同点。它被标记为 “一致方程” 和 “独立方程”。第二个图有三个平行平面，没有共同点。它被标记为系统不一致。在第三张图中，两个平面重合并平行于第三个平面。飞机没有共同之处。在第四张图中，两个平面是平行的，每个平面与第三个平面相交。飞机没有共同之处。在第五张图中，每个平面都与另外两个平面相交，但所有三个平面不共享任何点。飞机没有共同之处。在第六张图中，三个平面在一条直线上相交。只有一条线，所以有无限多的解决方案。在第七张图中，两个平面重合并且与第三个平面成一条直线相交。只有一条线，所以有无限多的解决方案。在最后一张图中，三个平面重合。只有一架飞机，所以有无限多的解决方案。$ $。$ $。$ $。$ $。$ $。$ $。$ $。$

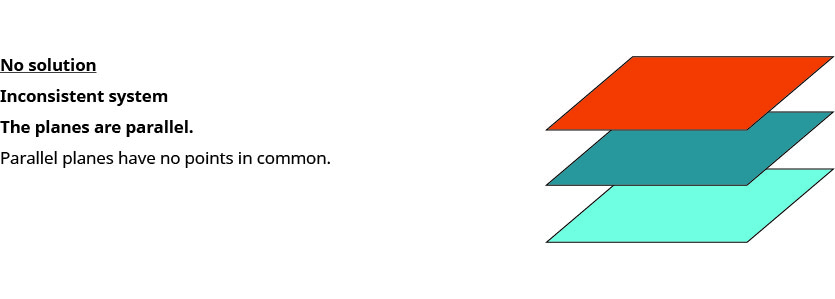
为了求解一个由三个线性方程组成的系统，我们要找出作为所有三个方程解的变量的值。换句话说，我们正在寻找使所有三个方程$(x,y,z)$都成真的有序三元组。这些被称为具有三个变量的三个线性方程组的解。

具有三个变量的线性方程组的解

方程组的解是使所有方程成真的变量的值。解由有序三元组表示$(x,y,z)$。

为了确定有序三元组是否是三个方程组的解，我们将变量的值代入每个方程中。如果有序三元组使所有三个方程都成立，则它是方程的解。

示例$\PageIndex{1}$

确定订购的三合一是否是系统的解决方案：$ \left\{ \begin{array} {l} x−y+z=2 \\ 2x−y−z=−6 \\ 2x+2y+z=−3 \end{array} \right. $

ⓐ$(−2,−1,3)$ ⓑ$(−4,−3,4)$

回答

ⓐ

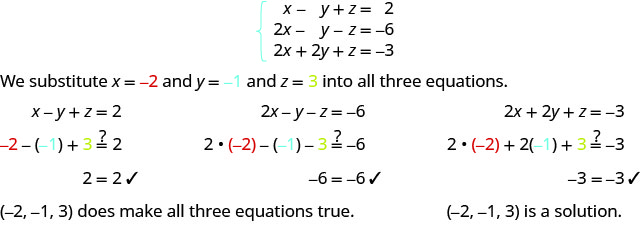
$方程为 x 减去 y 加 z 等于 2，2x 减去 y 减去 z 等于负 6，2x 加 2y 加 z 等于负 3。用负 2 代替 x，减去 1 代表 y，用 3 代替 z 到所有三个方程中，我们发现这三个方程都成立。因此，减去 2，减去 1，3 是一个解。$

ⓑ

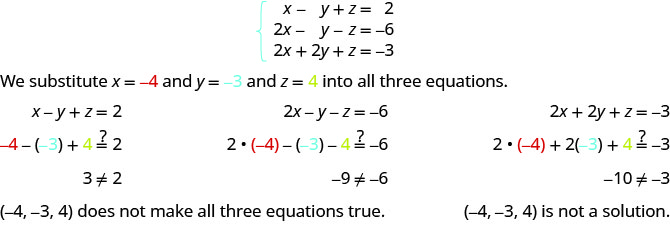
$方程为 x 减去 y 加 z 等于 2，2x 减去 y 减去 z 等于负 6，2x 加 2y 加 z 等于负 3。用减去 4 代替 x，减去 3 代表 y，用 4 代替 z，所有三个方程都成立。因此，减去 4，减去 3，4 不是解。$

示例$\PageIndex{2}$

确定订购的三合一是否是系统的解决方案：$ \left\{ \begin{array} {l} 3x+y+z=2 \\ x+2y+z=−3 \\ 3x+y+2z=4 \end{array} \right. $

ⓐ$(1,−3,2)$ ⓑ$(4,−1,−5)$

回答: ⓐ 是的 ⓑ 不

示例$\PageIndex{3}$

确定订购的三合一是否是系统的解决方案：$ \left\{ \begin{array} {l} x−3y+z=−5 \\ −3x−y−z=1 \\ 2x−2y+3z=1 \end{array} \right. $

ⓐ$(2,−2,3)$ ⓑ$(−2,2,3)$

回答: ⓐ 不 ⓑ 是的

求解具有三个变量的线性方程组

为了求解具有三个变量的线性方程组，我们基本上使用与具有两个变量的系统相同的技术。我们从两对方程开始，在每对方程中我们消除同一个变量。这将为我们提供一个只有两个变量的方程组，然后我们就知道如何求解这个方程组了！

接下来，我们使用刚才找到的两个变量的值返回原始方程并找到第三个变量。我们将答案写成有序三元组，然后检查结果。

示例$\PageIndex{4}$: How to Solve a System of Equations With Three Variables by Elimination

通过消除来解决系统：$ \left\{ \begin{array} {l} x−2y+z=3 \\ 2x+y+z=4 \\ 3x+4y+3z=−1 \end{array} \right. $

回答: $方程为 x 减去 2y 加 z 等于 3，2x 加 y 加 z 等于 4，3x 加 4y 加 3z 等于 1。步骤 1 是以标准形式编写方程式。他们是。如果有任何系数是分数，请将其清除。没有。$ $步骤 2 是从两个方程中消除同一个变量。决定要消除哪个变量。我们可以通过将方程 2 乘以 2 来消除方程 1 和 2 中的 y。使用一对方程来消除所选变量。将一个或两个方程相乘，使该变量的系数相对。将步骤 2 得出的方程相加，以消除一个变量。我们得到的新方程是 5x 加 3z 等于 11。$ $步骤 3 是使用另外两个方程重复步骤 2，并消除与步骤 2 中相同的变量。我们可以再次使用方程 1、3 通过将方程 1 乘以 2 来消除 y。将新方程相加，结果将为 5x 加 5z 等于 5。$ $第 4 步。这两个新方程形成了一个由两个方程和两个变量组成的系统。解决这个系统。消除 x，我们得到 z 等于负 3。将其代入其中一个新方程中，我们得到 x 等于 4。$ $步骤 5 是使用步骤 4 中找到的两个变量的值来查找第三个变量。将 x 和 z 的值代入其中一个原始方程中，我们得到 y 等于负 1。$ $步骤 6 是将解写为有序三重 4，减去 1，减去 3。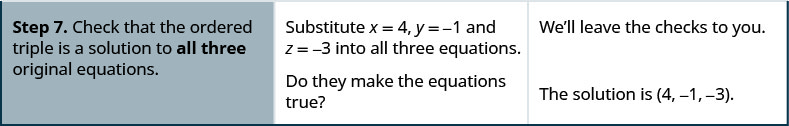$ $第 7 步是检查有序三元组是否是所有三个原始方程的解。它使所有三个方程都成真。$

示例$\PageIndex{5}$

通过消除来解决系统：$ \left\{ \begin{array} {l} 3x+y−z=2 \\ 2x−3y−2z=1 \\ 4x−y−3z=0 \end{array} \right.$

回答: $(2,−1,3)$

示例$\PageIndex{6}$

通过消除来解决系统：$ \left\{ \begin{array} {l} 4x+y+z=−1 \\ −2x−2y+z=2 \\ 2x+3y−z=1 \end{array} \right. $

回答: $(−2,3,4)$

此处总结了这些步骤。

求解具有三个变量的线性方程组。

用标准形式写出方程式
- 如果有任何系数是分数，请将其清除。
从两个方程中删除同一个变量。
- 决定要消除哪个变量。
- 使用一对方程来消除所选变量。
- 将一个或两个方程相乘，使该变量的系数相对。
- 将步骤 2 得出的方程相加，以消除一个变量
使用另外两个方程重复步骤 2，并消除与步骤 2 中相同的变量。
这两个新方程形成了一个由两个方程和两个变量组成的系统。解决这个系统。
使用步骤 4 中找到的两个变量的值来查找第三个变量。
将解写为有序三元组。
检查有序三元组是否是所有三个原始方程的解。

示例$\PageIndex{7}$

解决：$ \left\{ \begin{array} {l} 3x−4z=0 \\ 3y+2z=−3 \\ 2x+3y=−5 \end{array} \right. $

回答

\[ \left\{ \begin{array} {ll} 3x−4z=0 &(1) \\ 3y+2z=−3 &(2) \\ 2x+3y=−5 &(3) \end{array} \right. \nonumber \]

我们可以$z$从方程 (1) 和 (2) 中消除，方法是将方程 (2) 乘以 2，然后将所得方程相加。

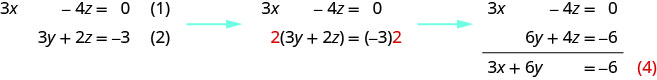
$方程为 3 x 减 4 等于 0，3y 加 2 z 等于负 3，2 x 加 3 y 等于负 5。将方程 2 乘以 2 并加到方程 1 中。我们得到 3 x 加 6 y 等于减去 6。$

请注意，方程 (3) 和 (4) 都有变量$x$和$y$。我们将为$x$和解决这个新系统$y$。

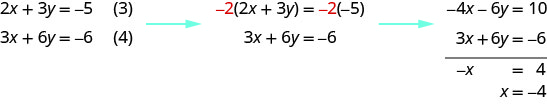
$将方程 3 乘以负 2，然后将其与方程 4 相加。我们得到 x 等于负 4。$

为了求解 y，我们用$x=−4$方程 (3) 代替。

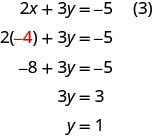
$用减去 4 代入方程 3 并求解 y。我们得到 y 等于 1。$

我们现在有$x=−4$和$y=1$。我们需要求解 z。我们可以代$x=−4$入方程 (1) 来找出 z。

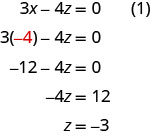
$将负 4 代入等于 x 的方程 1 中，我们得到 z 等于负 3。$

我们将解写为有序三元组。 $(−4,1,−3)$

我们检查解是否使所有三个方程都成立。

$\begin{array} {lll} {3x-4z=0 \space (1)} &{3y+2z=−3 \space (2)} &{2x+3y=−5 \space (3)} \\ {3(−4)−4(−3)\overset{?}{=} 0} &{3(1)+2(−3)\overset{?}{=} −3} &{2(−4)+3(1)\overset{?}{=} −5} \\ {0=0 \checkmark} &{−3=−3 \checkmark} &{−5=−5 \checkmark} \\ {} &{} &{\text{The solution is }(−4,1,−3)} \end{array}$

示例$\PageIndex{8}$

解决：$ \left\{ \begin{array} {l} 3x−4z=−1 \\ 2y+3z=2 \\ 2x+3y=6 \end{array} \right. $

回答: $(−3,4,−2)$

示例$\PageIndex{9}$

解决：$ \left\{ \begin{array} {l} 4x−3z=−5 \\ 3y+2z=7 \\ 3x+4y=6 \end{array} \right. $

回答: $(−2,3,−1)$

当我们求解一个系统但最终没有变量和错误陈述时，我们知道没有解决方案，而且系统不一致。下一个示例显示了一个不一致的方程组。

示例$\PageIndex{10}$

求解方程组：$ \left\{ \begin{array} {l} x+2y−3z=−1 \\ x−3y+z=1 \\ 2x−y−2z=2 \end{array} \right. $

回答

\[\left\{ \begin{array} {ll} x+2y−3z=−1 &(1) \\ x−3y+z=1 &(2) \\ 2x−y−2z=2 &(3) \end{array} \right.\nonumber \]

使用方程 (1) 和 (2) 消除 z。

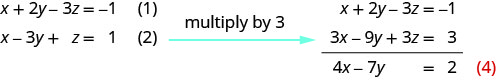
$方程为 x 加 2y 减去 3z 等于负 1，x 减去 3y 加 z 等于 1，2x 减去 y 减去 2z 等于 2。$

使用 (2) 和 (3)$z$ 再次消除。

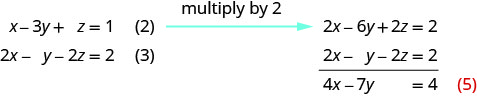
$将方程 2 乘以 3 并将其与方程 1 相加，得出方程 4，4x 减去 7y 等于 2。将方程 2 乘以 2 并将其与方程 3 相加，得出方程 5，4x 减去 7y 等于 4。$

使用 (4) 和 (5) 消除变量。

$方程 4 和 5 都有 2 个变量。将方程 5 乘以负 1 并将其与方程 4 相加。我们得到 0 等于减去 2，这是错误的。$

没有解决办法。

我们只剩下一个错误的陈述，这告诉我们系统不一致，没有解决方案。

示例$\PageIndex{11}$

求解方程组：$ \left\{ \begin{array} {l} x+2y+6z=5 \\ −x+y−2z=3 \\ x−4y−2z=1 \end{array} \right. $

回答: 没有解决办法

示例$\PageIndex{12}$

求解方程组：$ \left\{ \begin{array} {l} 2x−2y+3z=6 \\ 4x−3y+2z=0 \\ −2x+3y−7z=1 \end{array} \right. $

回答: 没有解决办法

当我们求解一个系统时，除了真实的陈述之外没有变量，我们就知道有无限多的解。该系统与因方程一致。我们的解决方案将显示其中两个变量如何依赖于第三个变量。

示例$\PageIndex{13}$

求解方程组：$ \left\{ \begin{array} {l} x+2y−z=1 \\ 2x+7y+4z=11 \\ x+3y+z=4 \end{array} \right. $

回答

\[\left\{ \begin{array} {ll} x+2y−z=1 &(1) \\ 2x+7y+4z=11 &(2) \\ x+3y+z=4 &(3) \end{array} \right.\nonumber \]

使用方程 (1) 和 (3) 消除 x。

$方程为 x 加 2y 减去 z 等于 1，2x 加 7y 加 4z 等于 11，x 加 3y 加 z 等于 4。将方程 1 乘以负 1 并将其与方程 3 相加。我们得到方程 4，y 加 2z 等于 3。$

使用方程 (1) 和 (2) 再次消除 x。

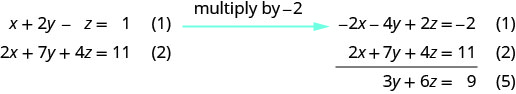
$将方程 1 乘以负 2 并将其与方程 2 相加。我们得到方程式 5，3y 加上 6z 等于 9。$

使用方程 (4) 和 (5) 消除$y$。

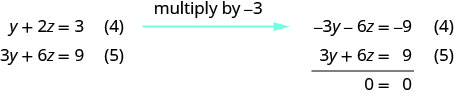
$将方程 4 乘以负 3 并将其与方程 5 相加。我们得到 0 等于 0。有无限多的解决方案。求解 y 的方程 4，我们得到 y 等于负 2z 加 3。用它代入方程 1，我们得到 x 等于 5z 减去 5。真正的陈述 0 等于 0 告诉我们这是一个有无限多解的依赖系统。解的形式为 x, y, z，其中 x 是 5z 减去 5，y 是负 2z 加 3，z 是任意实数。$

	有无限多的解决方案。
求解 y 的方程 (4)。	表示显示 x 和 y 如何依赖 z 的解。 $ \begin{aligned} y+2z &= 3 \\ y &= −2z+3 \end{aligned} $
使用方程 (1) 求解 x。	$ x+2y−z=1$
替代$y=−2z+3$。	$ \begin{aligned} x+2(−2z+3)−z &= 1 \\ x−4z+6−z &= 1 \\ x−5z+6 &= 1 \\ x &= 5z−5 \end{aligned} $

真实的陈$0=0$述告诉我们，这是一个依赖系统，有无限多的解决方案。解的形式为 (x, y, z) (x, y, z)$x=5z−5;\space y=−2z+3$，其中 z 是任意实数。

示例$\PageIndex{14}$

用方程求解方程组：$ \left\{ \begin{array} {l} x+y−z=0 \\ 2x+4y−2z=6 \\ 3x+6y−3z=9 \end{array} \right. $

回答: 无限多的解$(x,3,z)$哪里$x=z−3;\space y=3;\space z$是任何实数

示例$\PageIndex{15}$

用方程求解方程组：$ \left\{ \begin{array} {l} x−y−z=1 \\ −x+2y−3z=−4 \\ 3x−2y−7z=0 \end{array} \right. $

回答: 无限多的解$(x,y,z)$哪里$x=5z−2;\space y=4z−3;\space z$是任何实数

使用具有三个变量的线性方程组求解应用程序

由方程组建模的应用程序可以使用我们用于求解方程组的相同技术来求解。许多应用程序只是我们之前解决的三个类型的变量的扩展。

示例$\PageIndex{16}$

社区学院戏剧系出售了三种最新剧本制作的门票。成人票的售价为15美元，学生票的售价为10美元，儿童票的售价为8美元。剧院部门很高兴能在一晚售出250张门票并带来2,825美元的收入。售出的学生票数量是售出成人票数量的两倍。该部门每种类型销售了多少种？

回答

我们将使用图表来组织信息。	$。$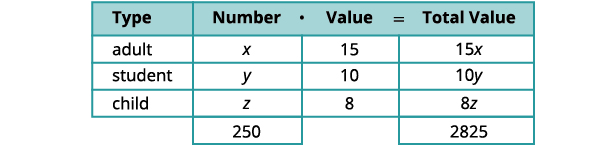
学生人数是成人人数的两倍。
以标准形式重写方程。	$\begin{aligned} y &= 2x \\ 2x−y &= 0 \end{aligned} $
$。$
使用方程 (1) 和 (2) 消除 z。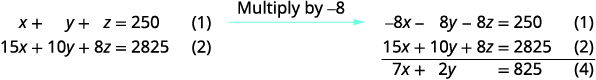
$。$
使用 (3) 和 (4) 消除$y$。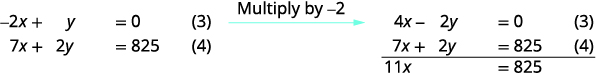
$。$
求解 x。	$x=75 $成人票
使用方程 (3) 求出 y。	$−2x+y=0$
替代$x=75$。	$\begin{aligned} −2(75)+y &= 0 \\ −150+y &= 0 \\ y &= 150\text{ student tickets}\end{aligned} $
使用方程 (1) 求出 z。	$x+y+z=250$
在值中替换 $x=75, \space y=150.$	$\begin{aligned} 75+150+z &= 250 \\ 225+z &= 250 \\ z &= 25\text{ child tickets} \end{aligned} $
写出解决方案。	剧院部门售出了 75 张成人票、 150 张学生门票和 25 张儿童票。

示例$\PageIndex{17}$

社区学院美术系出售了三种最新舞蹈表演的门票。成人票售价为20美元，学生票售价为12美元，儿童票售价为10美元。美术系很高兴能在一晚售出350张门票并带来4,650美元。售出的儿童票数量与售出的成人票数量相同。该部门每种类型销售了多少种？

回答: 美术系售出了 75 张成人票、200 张学生门票和 75 张儿童票。

示例$\PageIndex{18}$

社区大学足球队出售了三种最新比赛的门票。成人票的售价为10美元，学生票的售价为8美元，儿童票的售价为5美元。足球队很高兴售出600张门票，为一场比赛带来了4,900美元的收入。成人票的数量是儿童票数量的两倍。这支足球队每种类型卖了多少？

回答: 足球队售出了 200 张成人票、300 张学生门票和 100 张儿童票。

访问此在线资源，获取更多指导和练习，用三个变量求解一个没有解或无限解的线性系统。

用无解或无穷解的三个变量求解线性方程组
3 可变应用程序

关键概念

三个变量中的线性方程：具有三个变量的线性方程，其中 a、b、c 和 d 是实数，a、b 和 c 不全是 0，其形式为
\[ax+by+cz=d\nonumber \]

方程的每个解都是一个有序三元组，$(x,y,z)$这使得方程成真。
如何求解具有三个变量的线性方程组。
1. 以标准形式写出方程
  如果有任何系数是分数，请将其清除。
2. 从两个方程中删除同一个变量。
  决定要消除哪个变量。
  使用一对方程来消除所选变量。
  将一个或两个方程相乘，使该变量的系数相反。
  将步骤 2 得出的方程相加，以消除一个变量
3. 使用另外两个方程重复步骤 2，并消除与步骤 2 中相同的变量。
4. 这两个新方程形成了一个由两个方程和两个变量组成的系统。解决这个系统。
5. 使用步骤 4 中找到的两个变量的值来查找第三个变量。
6. 将解写为有序三元组。
7. 检查有序三元组是否是所有三个原始方程的解。

词汇表

具有三个变量的线性方程组的解: 方程组的解是使所有方程成真的变量的值；解由有序三元组（x、y、z）表示。

	有无限多的解决方案。
求解 y 的方程 (4)。	表示显示 x 和 y 如何依赖 z 的解。 \( \begin{aligned} y+2z &= 3 \\ y &= −2z+3 \end{aligned} \)
使用方程 (1) 求解 x。	\( x+2y−z=1\)
替代\(y=−2z+3\)。	\( \begin{aligned} x+2(−2z+3)−z &= 1 \\ x−4z+6−z &= 1 \\ x−5z+6 &= 1 \\ x &= 5z−5 \end{aligned} \)

三个变量中的线性方程

具有三个变量的线性方程组的解

示例\(\PageIndex{1}\)

示例\(\PageIndex{2}\)

示例\(\PageIndex{3}\)

示例\(\PageIndex{4}\): How to Solve a System of Equations With Three Variables by Elimination

示例\(\PageIndex{5}\)

示例\(\PageIndex{6}\)

求解具有三个变量的线性方程组。

示例\(\PageIndex{7}\)

示例\(\PageIndex{8}\)

示例\(\PageIndex{9}\)

示例\(\PageIndex{10}\)

示例\(\PageIndex{11}\)

示例\(\PageIndex{12}\)

示例\(\PageIndex{13}\)

示例\(\PageIndex{14}\)

示例\(\PageIndex{15}\)

示例\(\PageIndex{16}\)

示例\(\PageIndex{17}\)

示例\(\PageIndex{18}\)