4.3：使用方程组求解应用程序

学习目标

在本节结束时，您将能够：

• 解决直接翻译应用程序
• 求解几何应用程序
• 解决均匀运动应用程序

在开始之前，请参加这个准备测验。

1. 两个数字和九的总和为 31。 找到号码。
   如果你错过了这个问题，请查看 [链接]。
2. 双胞胎乔恩和罗恩去年共赚了96,000美元。 罗恩赚了8000美元，是乔恩收入的三倍。 每对双胞胎赚了多少钱？
   如果你错过了这个问题，请查看 [链接]。
3. 特快列车和当地火车离开匹兹堡前往华盛顿特区。特快列车可以在四个小时内出行，而当地火车则需要五个小时才能到达。 特快列车的速度比当地列车的速度快12英里/小时。 找出两列火车的速度。
   如果你错过了这个问题，请查看 [链接]。

解决直接翻译应用程序

线性方程组对于求解应用程序非常有用。 有些人发现用两个变量设置单词问题比只用一个变量设置它们要容易。 为了求解应用程序，我们首先要将单词翻译成线性方程组。 然后我们将决定最方便的使用方法，然后解决系统。

使用方程组求解应用程序。

1. 阅读问题。 确保所有文字和想法都被理解。
2. 确定我们在寻找什么。
3. 说出我们要找的东西。 选择变量来表示这些数量。
4. 转换为方程组。
5. 使用良好的代数技巧求解方程组。
6. 检查问题中的答案并确保答案合理。
7. 用完整的句子@@ 回答问题。

我们之前用一个变量解决了数字问题。 让我们看看它使用两个变量的工作原理有何不同。

两个数字的总和为零。 一个数字比另一个数字少九个。 找到数字。

回答

第 1 步。 阅读问题。
第 2 步。 确定我们在寻找什么。	我们正在寻找两个数字。
第 3 步。 说出我们要找的东西。	让\(n= \text{the first number} \)。 \(m= \text{the second number} \)
第 4 步。 转换为方程组。	两个数字的总和为零。
	一个数字比另一个数字少九个。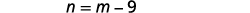
系统是：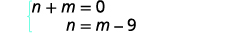
第 5 步。 求解 方程组。 我们将使用替换， 因为第二个方程为 n 求解。
在第一个方程中用 m − 9 代替 n。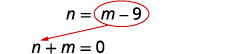
求解 m。
代\(m=\frac{9}{2}\)入第二个方程， 然后求解 n。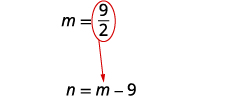
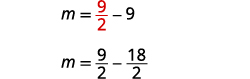
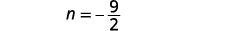
第 6 步。 检查问题中的答案。	这些数字在问题中有 意义吗？ 我们会把这个留给 你！
第 7 步。 回答问题。	数字是\(\frac{9}{2}\)和\(−\frac{9}{2}\)。

示例\(\PageIndex{2}\)

两个数字的总和为 10。 一个数字比另一个数字少 4。 找到数字。

回答

\(3, 7\)

示例\(\PageIndex{3}\)

两个数字的总和为\(−6\)。 一个数字比另一个数字少 10。 找到数字。

回答

\(2, −8\)

希瑟在健身房当教练的薪水有两种选择。 选项 A 将向她支付 25,000 美元，另加每次训练的 15 美元。 选项B将\($10,000+$40\)为她支付每次训练的费用。 多少次培训会使薪资选择相等？

回答

第 1 步。 阅读问题。
第 2 步。 确定我们在寻找什么。	我们正在寻找能够使薪酬相等 的 培训课程数量。
第 3 步。 说出我们要找的东西。	让 s=s= 希瑟的薪水。 n=n= 训练课程的次数
第 4 步。 转换为方程组。	选项 A 将向她支付 25,000 美元， 另加每次 训练的 15 美元。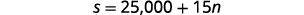
	选项 B 将为每次培训课程向她支付 10,000 美元 + 40 美元。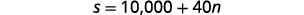
系统如图所示。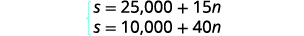
第 5 步。 求解方程组。 我们将使用替代。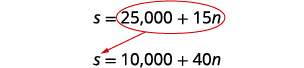
在第二个 方程中用 25,000 +15 n 代替 s。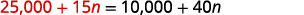
求解 n。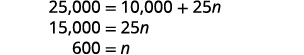
第 6 步。 检查答案。	每年 600 次培训课程是否合理？ 当 n = 600 时，这两个选项是否相等？
第 7 步。 回答问题。	600 次培训课程的薪金选项将相同。

示例\(\PageIndex{5}\)

两家保险公司向杰拉尔丁提供了职位。 第一家公司为每售出一张保单支付12,000美元的薪水外加100美元的佣金。 第二个支付20,000美元的工资，每售出一张保单加50美元的佣金。 需要出售多少保单才能使总工资保持不变？

回答

160 个策略

示例\(\PageIndex{6}\)

Kenneth目前以22,000美元的薪水为A公司出售西装，每售出一套西装可获得10美元的佣金。 B公司为他提供薪水为28,000美元的职位，每售出一套西装可获得4美元的佣金。 Kenneth 需要卖出多少套西装才能使期权相等？

回答

1000 套西装

在求解每个应用程序时，记得分析哪种求解方程组的方法最方便。

示例\(\PageIndex{7}\)

转换为方程组然后求解：

当 Jenna 在椭圆训练器上花了 10 分钟，然后进行了 20 分钟的循环训练时，她的健身应用程序显示她消耗了 278 卡路里的热量。 当她在椭圆机训练器上花 20 分钟和 30 分钟循环训练时，她消耗了 473 卡路里的热量。 在椭圆训练机上，她每分钟消耗多少卡路里？ 每分钟循环训练需要多少卡路里？

回答

第 1 步。 阅读问题。
第 2 步。 确定我们在寻找什么。	我们正在寻找 椭圆训练器每分钟 消耗的卡路里数量，以及每分钟循环训练消耗的卡 路里数量。
第 3 步。 说出我们要找的东西。	让 e=e= 椭圆训练机每 分钟消耗的卡路里数。 c=c= 循环训练时每 分钟消耗的卡路里数
第 4 步。 转换为方程组。	在椭圆机上 10 分钟和循环 训练 20 分钟，消耗 278 卡路里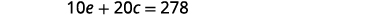
	在椭圆机上 20 分钟和 30 分钟的循环训练消耗了 473 卡路里的热量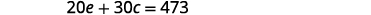
系统是：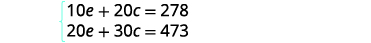
第 5 步。 求解方程组。
将第一个方程乘以 −2 得到 e 的 相反系数。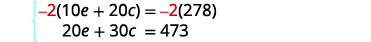
简化并添加方程。 求解 c。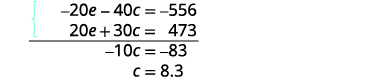
将 c = 8.3 替换为 原始方程之一来求解 e。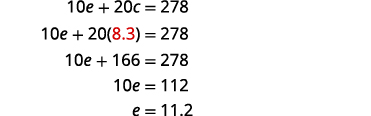
第 6 步。 检查问题中的答案。	自己检查数学。
第 7 步。 回答问题。	Jenna 在使用椭圆机训练时每分钟 消耗 8.3 卡路里的热量，每 分钟消耗 11.2 卡路里的热量。

示例\(\PageIndex{8}\)

转换为方程组然后求解：

Mark 去健身房做了 40 分钟的 Bikram 热瑜伽和 10 分钟的跳千斤顶。 他消耗了 510 卡路里的热量。 下次他去健身房时，他做了 30 分钟的 Bikram 热瑜伽和 20 分钟的跳千斤顶，消耗 470 卡路里的热量。 瑜伽每分钟消耗多少卡路里？ 每跳千斤顶消耗多少卡路里？

回答

Mark 每分钟瑜伽消耗 11 卡路里的热量，每分钟跳千斤顶消耗 7 卡路里的热量。

示例\(\PageIndex{9}\)

转换为方程组然后求解：

艾琳花了 30 分钟在划船机上，在健身房举重 20 分钟，消耗了 430 卡路里的热量。 下次去健身房时，她在划船机上花了50分钟，举重花了10分钟，消耗了600卡路里的热量。 她在划船机上每分钟消耗多少卡路里？ 她每举重一分钟消耗多少卡路里？

回答

艾琳在划船机上每分钟消耗 11 卡路里的热量，每举重一分钟消耗 5 卡路里的热量。

求解几何应用程序

现在，我们将使用线性方程组求解几何应用程序。 我们需要在列表中添加互补角和补充角度的一些属性。

两个互补角度的测量值相加为 90 度。 两个补充角度的测量值相加为 180 度。

互补角和补充角度

如果两个角度的测量值之和为 90 度，则这两个角度是互补的。

如果两个角度的测量值之和为 180 度，则两个角度是补充的

如果两个角度是互补的，我们说一个角度是另一个角度的补充。

如果两个角度是互补的，我们说一个角度是另一个角度的补充。

示例\(\PageIndex{10}\)

转换为方程组然后求解。

两个互补角的差为 26 度。 找到角度的测量值。

回答

\(\begin{array} {ll} {\textbf{Step 1. Read }\text{the problem.}} &{} \\ {\textbf{Step 2. Identify }\text{what we are looking for.}} &{\text{We are looking for the measure of each}} \\ {} &{\text{angle.}} \\ {\textbf{Step 3. Name }\text{what we are looking for.}} &{\text{Let} x=\text{ the measure of the first angle.}} \\ {} &{\hspace{3mm} y= \text{ the measure of the second angle}} \\ {\textbf{Step 4. Translate }\text{into a system of}} &{\text{The angles are complementary.}} \\ {\text{equations.}} &{\hspace{15mm} x+y=90} \\ {} &{\text{The difference of the two angles is 26}} \\ {} &{\text{degrees.}} \\ {} &{\hspace{15mm} x−y=26} \\ {} &{} \\ {} &{} \\ {\text{The system is shown.}} &{\hspace{15mm} \left\{ \begin{array} {l} x+y=90 \\ x−y=26 \end{array} \right. } \\ {} &{} \\ {} &{} \\ {\textbf{Step 5. Solve }\text{the system of equations} } &{\hspace{15mm} \left\{ \begin{array} {l} x+y=90 \\ \underline{x−y=26} \end{array} \right. } \\ {\text{by elimination.}} &{\hspace{21mm} 2x\hspace{4mm}=116} \\ {} &{\hspace{28mm} x=58} \\ {} &{} \\ {} &{} \\ {\text{Substitute }x=58\text{ into the first equation.}} &{\hspace{15mm} x+y=90} \\ {} &{\hspace{14mm} 58+y=90} \\ {} &{\hspace{22mm} y=32} \\ {\textbf{Step 6. Check }\text{the answer in the problem.}} &{} \\ {} &{} \\ {} &{} \\ {} &{} \\ {\hspace{15mm} 58+32=90\checkmark} &{} \\ {\hspace{15mm} 58−32=26\checkmark} &{} \\ {\textbf{Step 7. Answer }\text{the question.}} &{\text{The angle measures are 58 and 32 degrees.}} \end{array} \)

示例\(\PageIndex{11}\)

转换为方程组然后求解：

两个互补角度的差为 20 度。 找到角度的测量值。

回答

角度测量值为 55 和 35。

示例\(\PageIndex{12}\)

转换为方程组然后求解：

两个互补角的差为 80 度。 找到角度的测量值。

回答

角度测量值为 5 和 85。

在下一个示例中，我们记得补充角度的测量值加起来为 180。

示例\(\PageIndex{13}\)

转换为方程组然后求解：

两个角度是互补的。 较大角度的测量值比小于小角度的五倍。 找出两个角度的测量值。

回答

第 1 步。 阅读问题。
第 2 步。 确定我们在寻找什么。	我们正在寻找每个 角度的测量方法。
第 3 步。 说出我们要找的东西。	假设 x=x= 第一个角度的度量。 y=y= 第二个角度的度量
第 4 步。 转换为方程组。	角度是补充性的。
	较大的角度为十二小于较小角度的五 倍。
系统如下所示： 步骤 5。 求解方程替换系统。
在第一个方程中用 5 x − 12 代替 y。 求解 x。
在第二个 方程中用 32 代替 x，然后求解 y。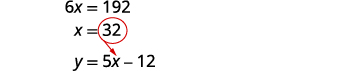
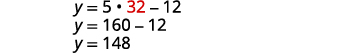
第 6 步。 检查问题中的答案。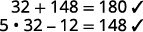
第 7 步。 回答问题。	角度测量值分别为 148 和 32 度。

示例\(\PageIndex{14}\)

转换为方程组然后求解：

两个角度是互补的。 较大角度的测量值是小角度的三倍多 12 度。 找到角度的测量值。

回答

角度测量值为 42 和 138。

示例\(\PageIndex{15}\)

转换为方程组然后求解：

两个角度是互补的。 较大角度的测量值为 18 小于较小角度的两倍。 找到角度的测量值。

回答

角度测量值为 66 和 114。

回想一下，三角形的角度加起来为 180 度。 直角三角形的角度为 90 度。 关于其他两个角度，这能告诉我们什么？ 在下一个示例中，我们将找到其他两个角度的测量值。

示例\(\PageIndex{16}\)

直角三角形中一个小角度的测量值是另一个小角度的三倍以上的十倍。 找出两个角度的测量值。

回答

我们将画一个人物并贴上标签。

第 1 步。 阅读问题。
第 2 步。 确定你在找什么。	我们正在寻找角度的测量方法。
第 3 步。 说出我们要找的东西。	假设 a=a= 第一个角度的度量。 b=b= 第二个角度的度量
第 4 步。 转换为方程组。	直角三角形中一个小角度的测量值是另一个小角度的三倍以上的十倍。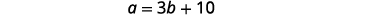
	三角形角度的测量总和为 180。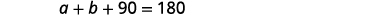
系统如图所示。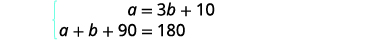
第 5 步。 求解方程组。 我们将使用替换，因为第一个方程已求解 a。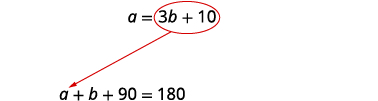
在第二个方程中，用 3b+103b+10 代替 a。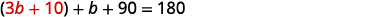
求解 b。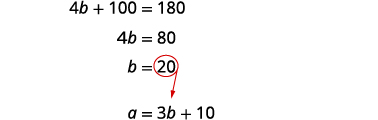
将 b=20b=20 替换到第一个方程中，然后求解 a。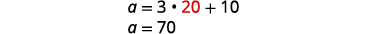
第 6 步。 检查问题中的答案。	我们会把这个留给你！
第 7 步。 回答问题。	小角度的测量值为 20 和 70 度。

示例\(\PageIndex{17}\)

直角三角形中一个小角度的测量值是另一个小角度的测量值的 2 倍多 3 倍。 找到两个角度的测量值。

回答

\(22, 68\)

示例\(\PageIndex{18}\)

直角三角形中一个小角度的测量值小于 18，小于另一个小角度的两倍。 找到两个角度的测量值。

回答

\(36, 54\)

在求解几何应用程序时，绘制图片以可视化情况通常很有帮助。

示例\(\PageIndex{19}\)

转换为方程组然后求解：

兰德尔有 125 英尺的围栏来封闭他家附近的后院部分。 他只需要围绕三面围栏，因为第四面将是房屋的墙壁。 他希望围栏院子（与房屋墙壁平行）的长度是宽度的四倍多 5 英尺。 找出长度和宽度。

回答

第 1 步。 阅读问题。
第 2 步。 确定你在找什么。	我们正在寻找长度和宽度。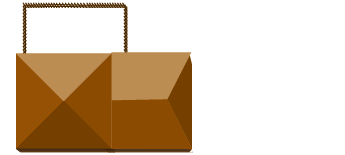
第 3 步。 说出我们要找的东西。	假设 L=L = 围栏码的长度。 W=W= 围栏院子的宽度
第 4 步。 转换为方程组。	一个长度和两个宽度等于 125。
	长度将超过宽度的 四倍 5 英尺。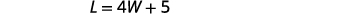
系统如图所示。 第 5 步。 通过替换求解方程组。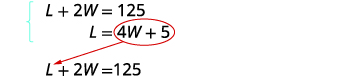
用 L = 4 W + 5 代入第一个 方程，然后求解 W。
在第二个 方程中用 20 代替 W，然后求解 L。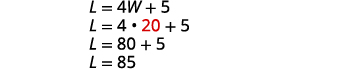
第 6 步。 检查 问题中的答案。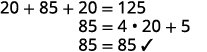
第 7 步。 回答方程式。	长度为 85 英尺，宽度为 20 英尺。

示例\(\PageIndex{20}\)

转换为方程组然后求解：

马里奥想在他后院的游泳池周围放一道围栏。 由于一侧与房屋相邻，他只需要将三面围起来。 有两个长边，一个较短的一边与房子平行。 他需要 155 英尺的围栏来封闭游泳池。 长边的长度小于 10 英尺，小于宽度的两倍。 找出要封闭的泳池区域的长度和宽度。

回答

长度为 60 英尺，宽度为 35 英尺。

示例\(\PageIndex{21}\)

转换为方程组然后求解：

亚历克西斯想在邻居围栏旁边的院子里建造一只矩形的狗跑。 她将使用 136 英尺的围栏将矩形狗跑道完全封闭。 狗沿着邻居围栏奔跑的长度将小于宽度的两倍16英尺。 找出狗跑的长度和宽度。

回答

长度为 60 英尺，宽度为 38 英尺。

解决均匀运动应用程序

前面介绍均匀运动问题时，我们使用表格来整理这些问题的信息。 我们将继续使用此表。 基本方程是\(D=rt\)其中 D 是行进距离，r 是速率，t 是时间。

我们的第一个均匀运动应用示例将针对类似于我们已经看到的情况，但现在我们可以使用两个变量和两个方程了。

示例\(\PageIndex{22}\)

转换为方程组然后求解：

乔尼在州际公路上离开圣路易斯，以每小时 65 英里的速度向西行驶向丹佛。 半小时后，凯利以与乔尼相同的路线离开圣路易斯，每小时行驶78英里。 凯利要多久才能赶上 Joni？

回答

图表有助于我们直观地了解情况。

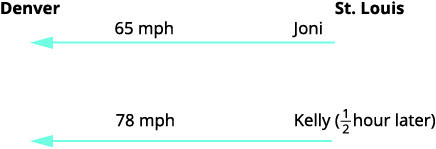
识别并命名我们要找的东西。 图表将帮助我们整理数据。 我们知道 Joni 和 Kelly 的汇率，因此我们在图表中输入了它们。 我们正在寻找 Kelly、k 和 Joni、j 各自开车的时间长度。

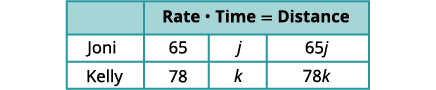
因为\(D=r·t\)我们可以填写距离栏。

转换为方程组。

要形成方程组，我们必须认识到 Kelly 和 Joni 的行驶距离相同。 所以，

\(\hspace{85mm} 65j=78k \nonumber \)

另外，由于凯利稍后离开，她的时间将比乔尼的时间少\(\frac{1}{2}\)一个小时。 所以，

\( \hspace{105mm} k=j-\frac{1}{2} \nonumber \)

\(\begin{array} {ll} {\text{Now we have the system.}} &{\left\{ \begin{array} {l} k=j−\frac{1}{2} \\ 65j=78k \end{array} \right.} \\ {\textbf{Solve }\text{the system of equations by substitution.}} &{} \\ {} &{} \\ {\text{Substitute }k=j−12\text{ into the second equation,}} &{} \\ {\text{then solve for }j.} &{} \\ {} &{65j=78k} \\ {} &{65j=78(j−\frac{1}{2})} \\ {} &{65j=78j−39} \\ {} &{−13j=−39} \\ {} &{j=3} \\{\begin{array} {l} {\text{To find Kelly’s time, substitute }j=3 \text{ into the first}} \\ {\text{equation, then solve for }k.} \end{array} } &{k=j−\frac{1}{2}} \\ {} &{k=3−\frac{1}{2} } \\ {} &{k=\frac{5}{2} \text{ or } k=2\frac{1}{2}} \\ {\textbf{Check }\text{the answer in the problem.}} &{} \\ {\begin{array} {lllll} {\text{Joni}} &{3 \text{ hours}} &{(65\text{ mph})} &= &{195\text{ miles}} \\ {\text{Kelly}} &{2\frac{1}{2} \text{ hours}} &{(78\text{ mph})} &= &{195\text{ miles}} \end{array}} &{} \\ {\text{Yes, they will have traveled the same distance}} &{} \\{\text{when they meet.}} &{} \\ {\textbf{Answer }\text{the question.}} &{} \\ {} &{\text{Kelly will catch up to Joni in}} \\ {} &{2\frac{1}{2}\text{ hours. By then, Joni will}} \\ {} &{\text{have traveled }3 \text{ hours.}} \\ \end{array}\)

示例\(\PageIndex{23}\)

转换为方程组然后求解：

米切尔在州际公路上以每小时 60 英里的速度离开底特律向南驶向奥兰多。 一小时后，克拉克以每小时 75 英里的速度离开底特律，沿着与米切尔相同的路线行驶。 克拉克要花多长时间才能抓住米切尔？

回答

克拉克要花4个小时才能抓到米切尔

示例\(\PageIndex{24}\)

转换为方程组然后求解：

查理以平均每小时 36 英里的速度离开了他母亲的房子。 15 分钟\((\frac{1}{4} \text{ hour})\)后，他的妹妹 Sally 离开了同一条路线，平均时速为 42 英里。 莎莉要等多久才能赶上查理？

回答

莎莉要花\(112\)几个小时才能赶上查理。

许多现实世界中均匀运动的应用之所以出现，是因为水流或空气流对车辆实际速度的影响。 由于风流盛行，在美国，越野飞机向西飞行所需的时间通常比向东飞行更长。

让我们来看看在河上行驶的船。 根据船的行驶方向，水流要么减慢船速，要么加速。

下图显示了河流如何影响船只的实际行驶速度。 我们将船在静止水中的速度 b 和河流的速度称为 c。

这艘船正在向下游行驶，方向与河流的方向相同。 潮流有助于推动船只，因此船的实际速度比在静水中的速度快。 船的实际移动速度是\(b+c\)。

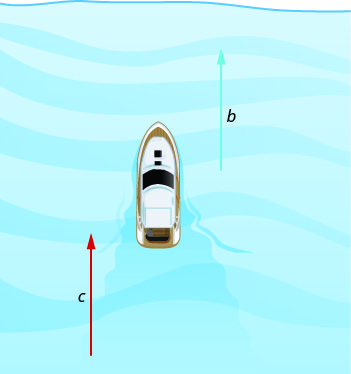
现在，船正在向上游行驶，正对着河流。 潮流不利于船，因此船的实际速度比它在静水中的速度慢。 船的实际速度是\(b−c\)。

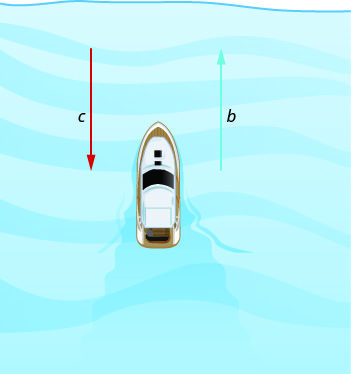
在下一个示例中，我们将为这种情况提供一些数字。

示例\(\PageIndex{25}\)

转换为方程组然后求解。

一艘内河游轮在下游航行了 60 英里，行驶了 4 个小时，然后花了 5 个小时向上游航行才返回码头。 找出船在静水中的速度和河流的速度。

回答

阅读问题。	这是一个均匀的运动问题，一 张照片可以帮助我们直观地看到情况。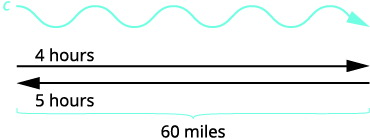
确定我们在寻找什么。	我们正在寻找飞船在静止水 中的速度和潮流的速度。
说出我们要找的东西。	让\(s= \text{the rate of the ship in still water.}\) \(c= \text{the rate of the current}\)
图表将帮助我们整理信息。 这艘船先下游再往上游。 向下游，潮流对 船舶有帮助，因此该船的实际费率为 s + c。 向上游移动，潮流会减慢飞船 的速度，因此实际速率为 s − c。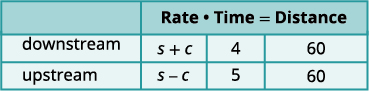
下游需要 4 个小时。 上游需要 5 个小时。 单程距离为 60 英里。
转换为方程组。 由于速率时间就是距离，我们可以 编写方程组。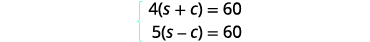
求解方程组。 Distribute 使两个方程都 采用标准形式，然后通过消法求解。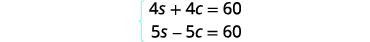
将顶部方程乘以 5，将 底部方程乘以 4。 添加方程，然后求解 s。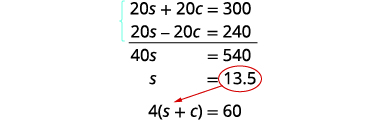
将 s = 13.5 替换为原始方 程式。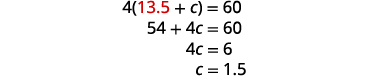
检查问题中的答案。 下游速度为 \(13.5+1.5=15\)英里每小时. 在 4 小时内船将行驶 \(15·4=60\)数英里。 上游速度为 \(13.5−1.5=12\)英里每小时. 在 5 小时内，船将行驶 \(12·5=60\)数英里。
回答问题。	飞船的速度为13.5英里/小时 ，目前的速度为1.5英里/小时。

示例\(\PageIndex{26}\)

转换为方程组然后求解：

密西西比河游船在上游航行 120 英里长达 12 个小时，然后花了 10 个小时才返回码头。 找出河船在静水中的速度和河流的速度。

回答

船的速度为11英里/小时，当前的速度为1英里/小时。

示例\(\PageIndex{27}\)

转换为方程组然后求解：

杰森在上游 24 英里处划了独木舟 4 个小时。 他花了 3 个小时才往后划桨。 找出独木舟在静水中的速度和河流的速度。

回答

独木舟的速度为7英里/小时，当前的速度为1英里/小时。

风流影响飞机速度的方式与水流影响船速的方式相同。 我们将在下一个示例中看到这一点。 与飞机飞行方向相同的风流称为顺风。 向飞机方向吹来的风流称为逆风。

示例\(\PageIndex{28}\)

转换为方程组然后求解：

私人飞机可以顺风在三个小时内飞行1,095英里，但在逆风后的三个小时内只能飞行987英里。 找出喷气机在静止空气中的速度和风速。

回答

阅读问题。	这是一个均匀的运动问题，一 张图片可以帮助我们进行可视化。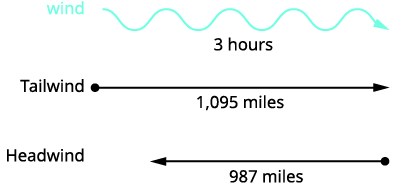
确定我们在寻找什么。	我们正在寻找喷气式飞机 在静止空气中的速度和风速。
说出我们要找的东西。	让 j=j= 喷气机在静止空气中的速度。 w=w= 风速。
图表将帮助我们整理信息。 喷气式飞机有两次飞行——一次是顺风 ，一次是逆风。 在顺风中，风有助于喷气式飞机，因此 速率为 j + w。 在逆风中，风会减慢喷气机的速度， 因此速率为 j − w。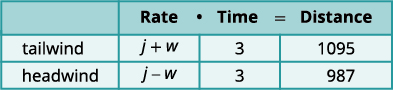
每次旅行需要 3 个小时。 飞机顺风飞行 1,095 英里。 在逆风中，喷气式飞机飞行了987英里。
转换为方程组。 由于速率时间就是距离，所以我们得到方 程组。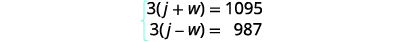
求解方程组。 分发，然后通过消除求解。 相加，然后求解 j。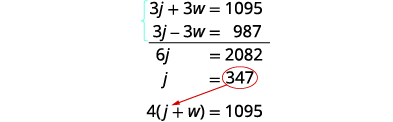
将 j = 347 替换为原始方 程之一，然后求解 w。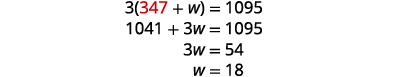
检查问题中的答案。 顺风, 喷气式飞机的实际速度将为 \(347+18=365\) mph. 在 3 小时内，喷气式飞机将行驶数 \(365·3=1,095\)英里 进入逆风，喷气式飞机的实际 速度将为 \(347−18=329\)英里每小时。 飞机将在3小时内行驶 \(329·3=987\)数英里。
回答问题。	喷气式飞机的速度为 347 英里/小时，风 速为 18 英里/小时。

示例\(\PageIndex{29}\)

转换为方程组然后求解：

一架小型喷气式飞机在顺风下可以在5小时内飞行1,325英里，但在逆风的5小时内只能飞行1,035英里。 找出喷气机在静止空气中的速度和风速。

回答

喷气式飞机的速度为 235 英里/小时，风速为 30 英里/小时。

示例\(\PageIndex{30}\)

转换为方程组然后求解：

一架商用飞机可以顺风在4小时内飞行1,728英里，但在逆风的4小时内只能飞行1,536英里。 找出喷气机在静止空气中的速度和风速。

回答

喷气式飞机的速度为 408 英里/小时，风速为 24 英里/小时。

访问此在线资源，获取有关方程组的更多指导和练习。

• 方程组

关键概念

• 如何使用方程组求解应用程序
  1. 阅读问题。 确保所有文字和想法都被理解。
  2. 确定我们在寻找什么。
  3. 说出我们要找的东西。 选择变量来表示这些数量。
  4. 转换为方程组。
  5. 使用良好的代数技巧求解方程组。
  6. 检查问题中的答案并确保答案合理。
  7. 用完整的句子@@ 回答问题。

词汇表

互补角度

如果两个角度的测量值之和为 90 度，则这两个角度是互补的。

补充角度

如果两个角度的测量总和为 180 度，则两个角度是补充的。