第 3 章复习练习

章节复习练习

绘制两个变量中的线性方程

在矩形坐标系中绘制点

在以下练习中，在矩形坐标系中绘制每个点。

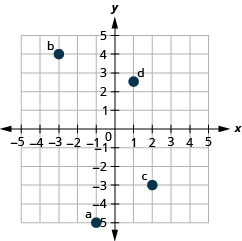
1. ⓐ$(−1,−5)$
ⓑ$(−3,4)$
ⓒ$(2,−3)$
ⓓ$(1,\frac{5}{2})$

回答

2. ⓐ$(−2,0)$
ⓑ$(0,−4)$
ⓒ$(0,5)$
ⓓ$(3,0)$

在以下练习中，确定哪些有序对是给定方程的解。

3。 $5x+y=10$;

ⓐ$(5,1)$
ⓑ$(2,0)$
ⓒ$(4,−10)$

回答

ⓑ, ⓒ

4。 $y=6x−2$;

ⓐ$(1,4)$
ⓑ$(13,0)$
ⓒ$(6,−2)$

通过绘制点来绘制线性方程图

在以下练习中，通过绘制点来绘制图形。

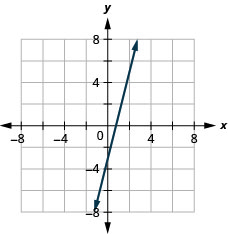
5。 $y=4x−3$

回答

6。 $y=−3x$

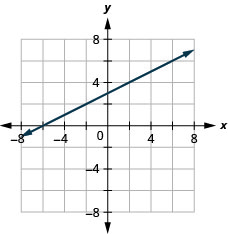
7。 $y=\frac{1}{2}x+3$

回答

8。 $y=−\frac{4}{5}|x−1$

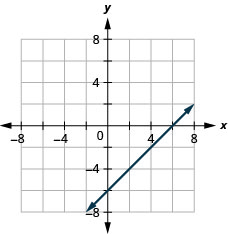
9。 $x−y=6$

回答

10。 $2x+y=7$

11。 $3x−2y=6$

回答

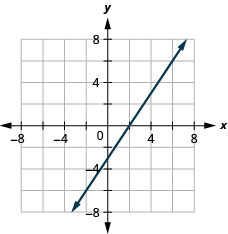
绘制垂直线和水平线

在以下练习中，绘制每个方程的图表。

12。 $y=−2$

13。 $x=3$

回答

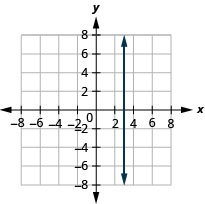
在以下练习中，用相同的矩形坐标系绘制每对方程的图形。

14。 $y=−2x$和$y=−2$

15。 $y=\frac{4}{3}x$和$y=\frac{4}{3}$

回答

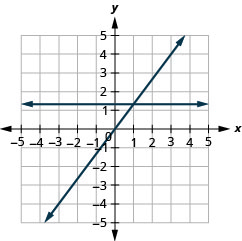
查找 x 和 y 截距

在以下练习中，找到 x 和 y 截距。

16。

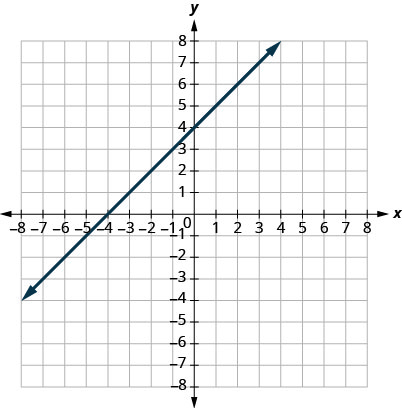
17。

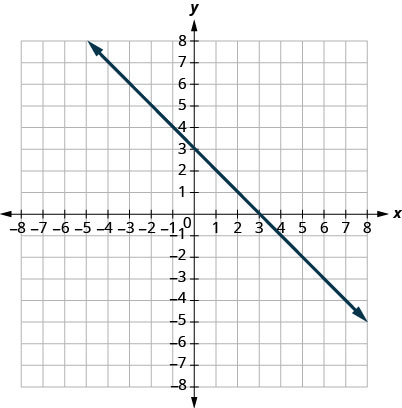
回答

$(0,3)(3,0)$

在以下练习中，找到每个方程的截距。

18。 $x−y=−1$

19。 $x+2y=6$

回答

$(6,0),\space (0,3)$

20。 $2x+3y=12$

21。 $y=\frac{3}{4}x−12$

回答

$(16,0),\space (0,−12)$

22。 $y=3x$

使用截图画一条线

在以下练习中，使用截获量绘制图表。

23。 $−x+3y=3$

回答

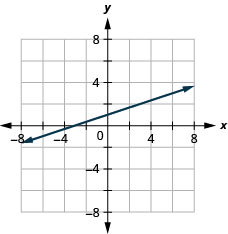
24。 $x−y=4$

25。 $2x−y=5$

回答

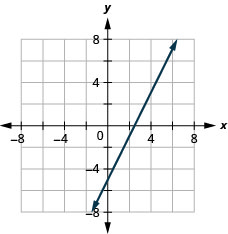
26。 $2x−4y=8$

27。 $y=4x$

回答

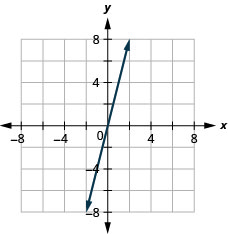
直线的斜率

找出直线的斜率

在以下练习中，找到所示每条线的斜率。

28。

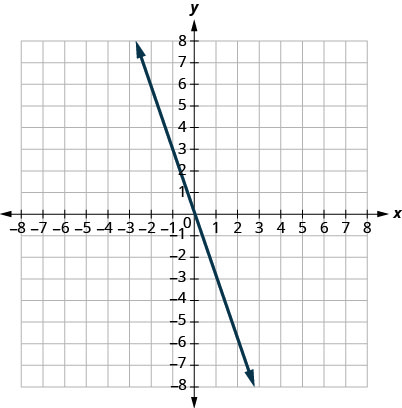
29。

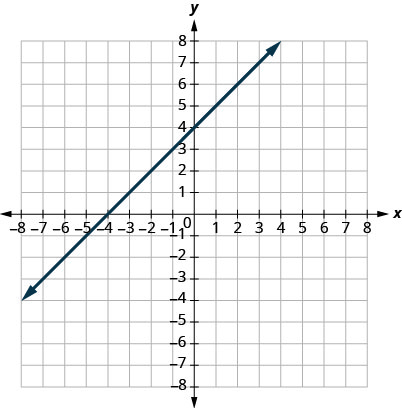
回答

1

30。

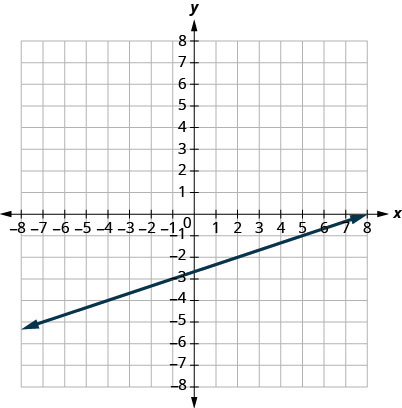
31。

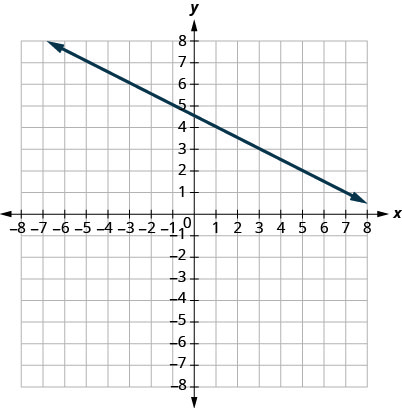
回答

$−12$

在以下练习中，找出每条线的斜率。

32。 $y=2$

33。 $x=5$

回答

未定义

34。 $x=−3$

35。 $y=−1$

回答

0

使用斜率公式求出两点间直线的斜率

在以下练习中，使用斜率公式求出每对点之间的直线的斜率。

36。 $(−1,−1),(0,5)$

37。 $(3.5),(4,−1)$

回答

$−6$

38。 $(−5,−2),(3,2)$

39。 $(2,1),(4,6)$

回答

$52$

给定一个点和斜率绘制一条直线

在以下练习中，用给定的点和斜率绘制每条线。

40。 $(2,−2);\space m=52$

41。 $(−3,4);\space m=−13$

回答

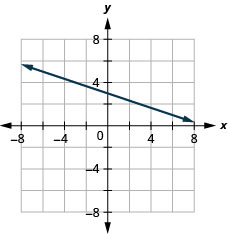
42。 $x$-截距$−4; m=3$

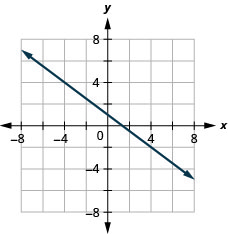
43。 $y$-截距$1; m=−34$

回答

使用斜率和截距绘制直线图

在以下练习中，确定每条线的斜率和$y$截距。

44。 $y=−4x+9$

45。 $y=53x−6$

回答

$m=53;\space (0,−6)$

46。 $5x+y=10$

47。 $4x−5y=8$

回答

$m=\frac{4}{5};\space (0,−\frac{8}{5})$

在以下练习中，使用每个方程的斜率和 y 截距绘制每个方程的直线。

48。 $y=2x+3$

49。 $y=−x−1$

回答

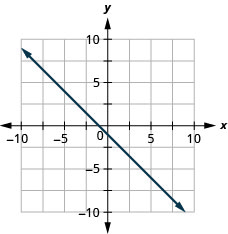
50。 $y=−25x+3$

51。 $4x−3y=12$

回答

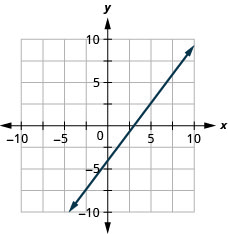
在以下练习中，确定绘制每条线的最便捷方法。

52。 $x=5$

53。 $y=−3$

回答

水平线

54。 $2x+y=5$

55。 $x−y=2$

回答

截住

56。 $y=22x+2$

57。 $y=34x−1$

回答

绘制点

绘制和解释斜率截距的应用

58。 凯瑟琳是一名私人厨师。 该方程$C=6.5m+42$模拟了她每周的费用 C（以美元计）与她供应的膳食数量 m 之间的关系。

ⓐ 查找凯瑟琳不提供餐食一周的费用。
ⓑ 找出她提供 14 顿饭时一周的费用。
ⓒ 解释方程的斜率和 C 截距。
ⓓ 绘制方程的图表。

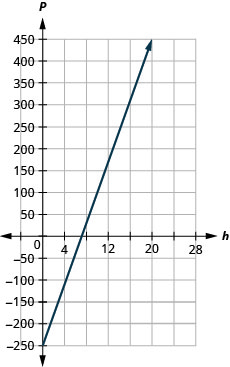
59。 玛乔丽教钢琴。 该方程$P=35h−250$模拟了她每周的利润 P（以美元计）与她所教的学生课数之间的关系。

ⓐ 查找 Marjorie 一周不教学生课时的利润。
ⓑ 当她教20节学生课时，可以找到一周的利润。
ⓒ 解释方程的斜率和 P 截距。
ⓓ 绘制方程的图表。

回答

ⓐ$−$250$
ⓑ$$450$
ⓒ 斜率为 35，意味着 Marjorie 每多上一次学生课，她的每周利润 P 就会增加 35 美元。
P-intercept 意味着当课程数量为 0 时，Marjorie 会损失 250 美元。
ⓓ

使用斜率识别平行线和垂直线

在以下练习中，使用斜率和$y$截距来确定两条线是平行、垂直还是两者都不平行。

60。 $4x−3y=−1;\quad y=43x−3$

61。 $y=5x−1;\quad 10x+2y=0$

回答

也不

62。 $3x−2y=5;\quad 2x+3y=6$

63。 $2x−y=8;\quad x−2y=4$

回答

不平行

求直线方程

给定斜率和 y 截距求直线方程

在以下练习中，找到具有给定斜率和 y 截距的直线的方程。 以斜率截距形式写下方程。

64。 斜$y$率$\frac{1}{3}$和截距$(0,−6)$

65。 斜$y$率$−5$和截距$(0,−3)$

回答

$y=−5x−3$

66。 斜$y$率$0$和截距$(0,4)$

67。 斜$y$率$−2$和截距$(0,0)$

回答

$y=−2x$

在以下练习中，找到每张图中显示的直线的方程。 以斜率截距形式写下方程。

68。

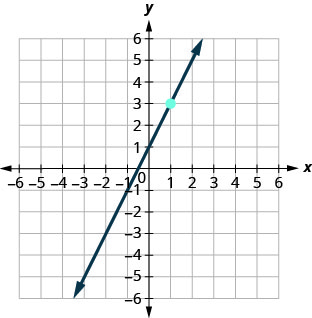
69。

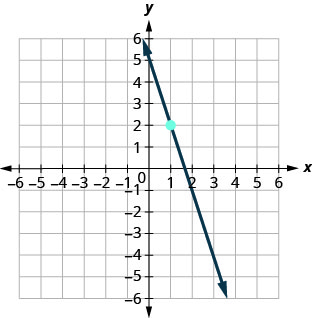
回答

$y=−3x+5$

70。

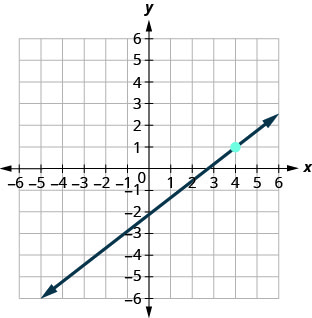
71。

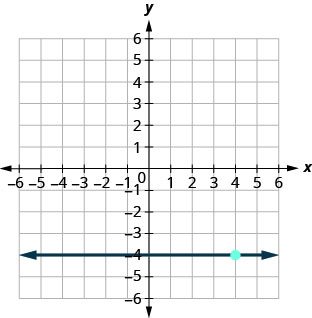
回答

$y=−4$

在给定斜率和点的情况下求直线方程

在以下练习中，找到具有给定斜率并包含给定点的直线的方程。 以斜率截距形式写下方程。

72。 $m=−\frac{1}{4}$，点$(−8,3)$

73。 $m=\frac{3}{5}$，点$(10,6)$

回答

$y=\frac{3}{5}x$

74。 水平线包含$(−2,7)$

75。 $m=−2$，点$(−1,−3)$

回答

$y=−2x−5$

给定两点求直线方程

在以下练习中，找到包含给定点的直线的方程。 以斜率截距形式写下方程。

76。 $(2,10)$和$(−2,−2)$

77。 $(7,1)$和$(5,0)$

回答

$y=\frac{1}{2}x−\frac{5}{2}$

78。 $(3,8)$和$(3,−4)$

79。 $(5,2)$和$(−1,2)$

回答

$y=2$

求一条平行于给定直线的直线的方程

在以下练习中，找到一条平行于给定直线且包含给定点的直线的方程。 以斜率截距形式写下方程。

80. 线$y=−3x+6$，点$(1,−5)$

81. 线$2x+5y=−10$，点$(10,4)$

回答

$y=−\frac{2}{5}x+8$

82. 线$x=4$，点$(−2,−1)$

83. 线$y=−5$，点$(−4,3)$

回答

$y=3$

求一条垂直于给定直线的直线的方程

在以下练习中，找到一条垂直于给定直线并包含给定点的直线的方程。 以斜率截距形式写下方程。

84. 线$y=−\frac{4}{5}x+2$，点$(8,9)$

85. 线$2x−3y=9$，点$(−4,0)$

回答

$y=−\frac{3}{2}x−6$

86. 线$y=3$，点$(−1,−3)$

87. 线$x=−5$点$(2,1)$

回答

$y=1$

绘制两个变量中的线性不等式

验证两个变量中不等式的解

在以下练习中，确定每个有序对是否是给定不等式的解。

88。 确定每个有序对是否是不等式的解$y<x−3$：

ⓐ$(0,1)$ ⓑ$(−2,−4)$ ⓒ$(5,2)$ ⓓ$(3,−1)$
ⓔ$(−1,−5)$

89。 确定每个有序对是否是不等式的解$x+y>4$：

ⓐ$(6,1)$ ⓑ$(−3,6)$ ⓒ$(3,2)$ ⓓ$(−5,10)$ ⓔ$(0,0)$

回答

ⓐ 是的 ⓑ 不 ⓒ 是的 ⓓ 是的；ⓔ nom

认识不等式解与其图之间的关系

在以下练习中，写下阴影区域所示的不等式。

90。 用边界线写下图所示的不等式$y=−x+2.$

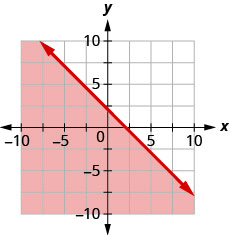
91。 用边界线写下图表所示的不等式$y=\frac{2}{3}x−3$。

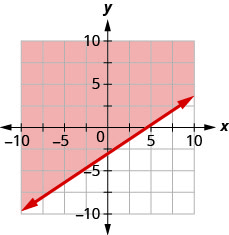
回答

$y>\frac{2}{3}x−3$

92。 用边界线写下图中阴影区域所示的不等式$x+y=−4$。

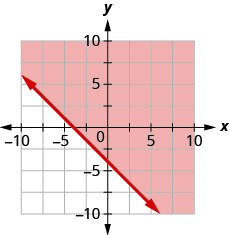
93。 用边界线写下图中阴影区域所示的不等式$x−2y=6$。

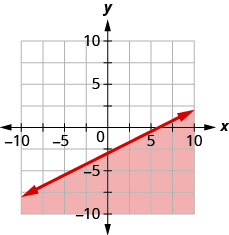
回答

$x−2y\geq 6$

绘制两个变量中的线性不等式

在以下练习中，绘制每个线性不等式的图表。

94。 绘制线性不等式图$y>\frac{2}{5}x−4$。

95。 绘制线性不等式图$y\leq −\frac{1}{4}x+3$。

回答

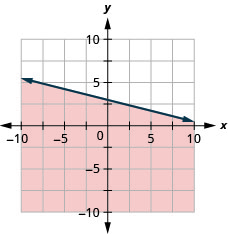
96。 绘制线性不等式图$x−y\leq 5$。

97。 绘制线性不等式图$3x+2y>10.$

回答

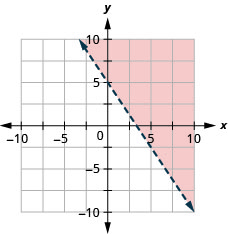
98。 绘制线性不等式图$y\leq −3x$。

99。 绘制线性不等式图$y<6.$

回答

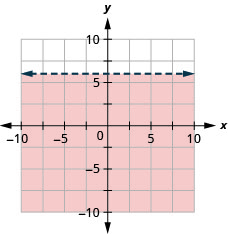
使用两个变量中的线性不等式求解应用程序

100。 Shanthie 在暑假期间每周至少需要赚取 500 美元才能支付大学学费。 她有两份工作。 一个是游泳教练，每小时支付10美元，另一个是律师事务所实习生，每小时25美元。 Shanthie 每份工作需要工作多少小时才能每周至少赚到 500 美元？

ⓐ 让 x 成为她教游泳的小时数，让 y 成为她作为实习生工作的小时数。 写一个不等式来模拟这种情况。
ⓑ 绘制不等式图。
ⓒ 找到三个可以解决$(x,y)$不等式的有序对。 然后，解释一下这对 Shanthie 意味着什么。

101。 Atsushi 他需要足够的运动才能每天$600$消耗卡路里。 他喜欢跑步或骑自行车，跑步时每分钟$20$消耗卡路里，骑自行车时每分钟$15$消耗卡路里。

ⓐ 如果 x 是 Atsushi 跑步的分钟数，y 是他骑自行车的分钟数，请找出模拟情况的不等式。
ⓑ 绘制不等式图。
ⓒ 列出不等式的三种解决方案。 这些解决方案为Atsushi提供了哪些选择？

回答

ⓐ$20x+15y\geq 60020x+15y\geq 600$
ⓑ

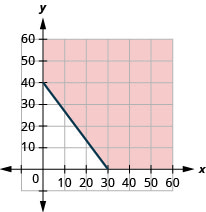
ⓒ 答案会有所不同。

关系和函数

找出关系的域和范围

在以下练习中，对于每个关系，ⓐ 找到关系的域 ⓑ 找到关系的范围。

102。 ${\{(5,−2),\,(5,−4),\,(7,−6),\,(8,−8),\,(9,−10)}\}$

103。 ${\{(−3,7),\,(−2,3),\,(−1,9), \,(0,−3),\,(−1,8)}\}$

回答

ⓐ$D: {−3, −2, −1, 0}$
ⓑ$R: {7, 3, 9, −3, 8}$

在以下练习中，使用关系映射到 ⓐ 列出关系的有序对 ⓑ 找到关系的域 ⓒ 找到关系的范围。

104。 下图显示了按年龄划分的儿童平均体重。

在以下练习中，使用关系图 ⓐ 列出关系的有序对 ⓑ 找到关系的域 ⓒ 找到关系的范围。

105。

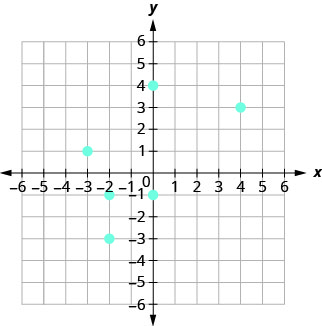
回答

ⓐ$(4, 3), \,(−2, −3), \,(−2, −1), \,(−3, 1), \,(0, −1), \,(0, 4)$
ⓑ$D: {−3, −2, 0, 4}$
ⓒ$R: {−3, −1, 1, 3, 4}$

确定关系是否为函数

在以下练习中，使用一组有序对来 ⓐ 确定关系是否为函数 ⓑ 找到关系的域 ⓒ 找到关系的范围。

106。 ${\{(9,−5),\,(4,−3),\,(1,−1),\,(0,0),\,(1,1),\,(4,3),\,(9,5)}\}$

107。 ${\{(−3,27),\,(−2,8),\,(−1,1),\,(0,0),\,(1,1),\,(2,8),\,(3,27)}\}$

回答

ⓐ 是的 ⓑ${−3, −2, −1, 0, 1, 2, 3}$
ⓒ${0, 1, 8, 27}$

在以下练习中，使用映射来 ⓐ 确定关系是否为函数 ⓑ 找到函数的域 ⓒ 找到函数的范围。

108。

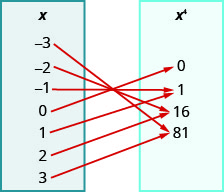
109。

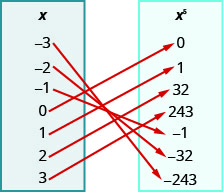
回答

ⓐ${−3, −2, −1, 0, 1, 2, 3}$
ⓑ${−3, −2, −1, 0, 1, 2, 3}$
ⓒ${−243, −32, −1, 0, 1, 32, 243}$

在以下练习中，确定每个方程是否为函数。

110。 $2x+y=−3$

111。 $y=x^2$

回答

是的

112。 $y=3x−5$

113。 $y=x^3$

回答

是的

114。 $2x+y2=4$

找出一个函数的值

在以下练习中，评估该函数：

ⓐ$f(−2)$ ⓑ$f(3)$ ⓒ$f(a)$。

115。 $f(x)=3x−4$

回答

ⓐ$f(−2)=−10$ ⓑ$f(3)=5$ ⓒ$f(a)=3a−4$

116。 $f(x)=−2x+5$

117。 $f(x)=x^2−5x+6$

回答

ⓐ$f(−2)=20$ ⓑ$f(3)=0$ ⓒ$f(a)=a^2−5a+6$

118。 $f(x)=3x^2−2x+1$

在以下练习中，评估该函数。

119。 $g(x)=3x2−5x;\space g(2)$

回答

$2$

120。 $F(x)=2x2−3x+1;\space F(−1)$

121。 $h(t)=4|t−1|+2;\space h(t)=4$

回答

$18$

122。 $f(x)=x+2x−1;\space f(3)$

函数图

使用垂直线测试

在以下练习中，确定每个图形是否是函数的图形。

123。

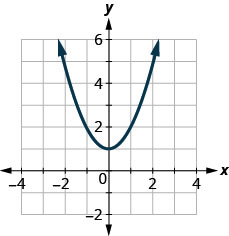
回答

是的

124。

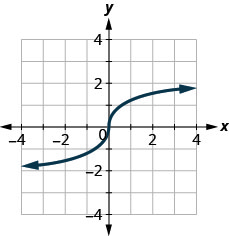
125。

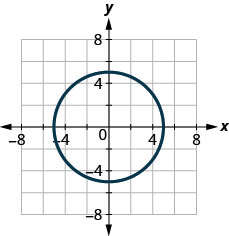
回答

不

126。

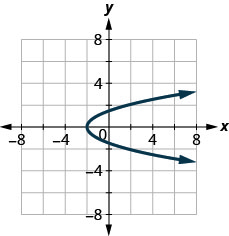
127。

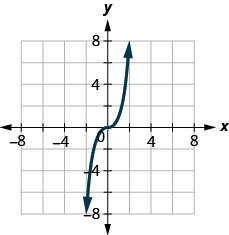
回答

是的

128。

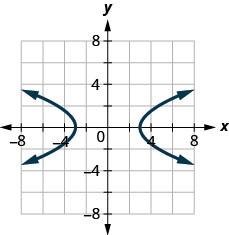
129。

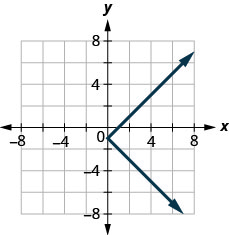
回答

不

识别基本函数的图表

在以下练习中，ⓐ 绘制每个函数的图形 ⓑ 陈述其域和范围。 用间隔表示法写下域和范围。

130。 $f(x)=5x+1$

131。 $f(x)=−4x−2$

回答

ⓐ

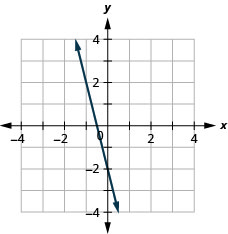
ⓑ$D: (-\inf ,\inf ), R: (-\inf ,\inf )$

132。 $f(x)=\frac{2}{3}x−1$

133。 $f(x)=−6$

回答

ⓐ

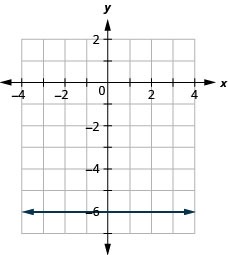
ⓑ$D: (-\inf ,\inf ), R: (-\inf ,\inf )$

134。 $f(x)=2x$

135。 $f(x)=3x^2$

回答

ⓐ

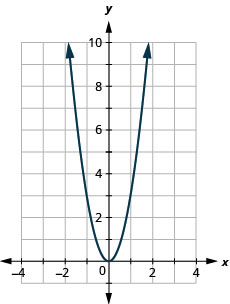
ⓑ$D: (-\inf ,\inf ), R: (-\inf ,0]$

136。 $f(x)=−12x^2$

137。 $f(x)=x^2+2$

回答

ⓐ

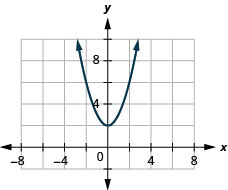
ⓑ$D: (-\inf ,\inf ), R: (-\inf ,\inf )$

138。 $f(x)=x^3−2$

139。 $f(x)=\sqrt{x+2}$

回答

ⓐ

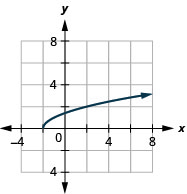
ⓑ$D: [−2,−2, \inf ), \space R: [0,\inf )$

140。 $f(x)=−|x|$

141。 $f(x)=|x|+1$

回答

ⓐ

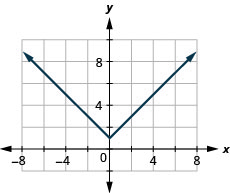
ⓑ$D: (-\inf ,\inf ), \space R: [1,\inf )$

从函数图中读取信息

在以下练习中，使用函数的图形来查找其域和范围。 用间隔表示法写下域和范围

142。

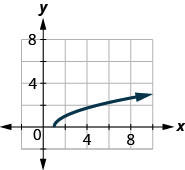
143。

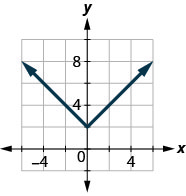
回答

$D: (-\inf ,\inf ), R: [2,\inf )$

144。

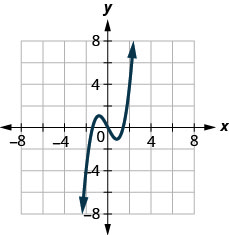
在以下练习中，使用函数的图形来查找指示的值。

145。

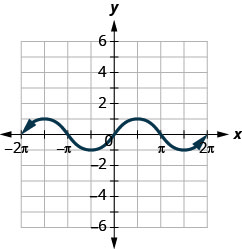
ⓐ 查找$f(0)$。
ⓑ 查找$f(12\pi )$。
ⓒ 查找$f(−32\pi )$。
ⓓ 找出$x$何时的值$f(x)=0$。
ⓔ 找到$x$-拦截。
ⓕ 找到$y$-截距。
ⓖ 找到域名。 用间隔符号书写。
ⓗ 找到范围。 用间隔符号书写。

回答

ⓐ$f(x)=0$ ⓑ$f(\pi /2)=1$
ⓒ$f(−3\pi /2)=1$ ⓓ f$f(x)=0$ or$x=−2\pi ,−\pi ,0,\pi ,2\pi$
ⓔ$(−2\pi ,0), (−\pi ,0), (0,0), (\pi ,0), (2\pi ,0)$ ⓕ$(0,0)$
ⓖ$[−2\pi ,2\pi ]$ ⓗ$[−1,1]$

146。

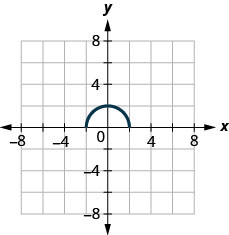
ⓐ 查找$f(0)$。
ⓑ 找出$x$何时的值$f(x)=0$。
ⓒ 找到$x$-拦截。
ⓓ 找到$y$-截距。
ⓔ 找到域名。 用间隔符号书写。
ⓕ 找到范围。 用间隔符号书写。

练习测试

1。 在矩形坐标系中绘制每个点。

ⓐ$(2,5)$
ⓑ$(−1,−3)$
ⓒ$(0,2)$
ⓓ$(−4,32)$
ⓔ$(5,0)$

回答

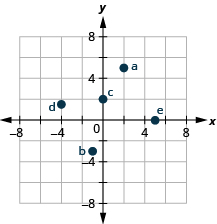
2。 给定的有序对中哪些是方程的解$3x−y=6$？

ⓐ$(3,3)$ ⓑ$(2,0)$ ⓒ$(4,−6)$

3。 找到所示每条线的斜率。

ⓐ

ⓑ

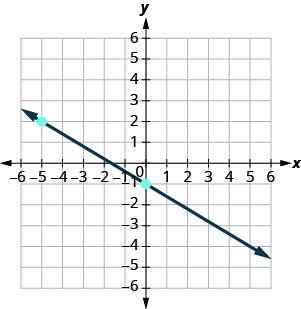
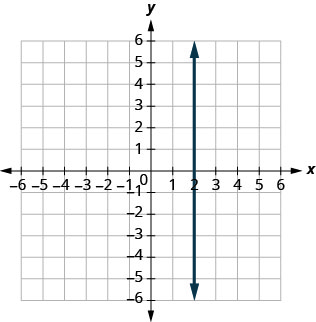
回答

ⓐ$−\frac{3}{5}$ ⓑ 未定义

4。 找出两点$(5,2)$和之间的直线的斜率$(−1,−4)$。

5。 用$\frac{1}{2}$包含该点的斜率绘制直线图$(−3,−4)$。

回答

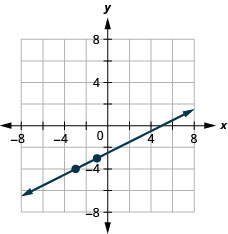
6。 找出$4x+2y=−8$和图形的截距。

绘制以下每个方程的直线。

7。 $y=\frac{5}{3}x−1$

回答

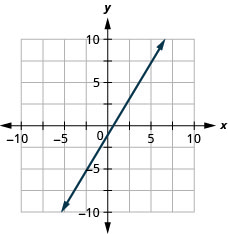
8。 $y=−x$

9。 $y=2$

回答

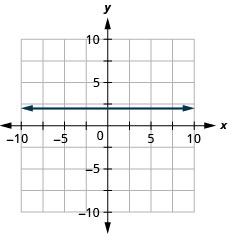
找出每条线的方程。 以斜率截距形式写出方程。

10. 斜$y$率$−\frac{3}{4}$和截距$(0,−2)$

11。 $m=2$，点$(−3,−1)$

回答

$y=2x+5$

12. 包含$(10,1)$和$(6,−1)$

13. 垂直于直线$y=\frac{5}{4}x+2$，包含点$(−10,3)$

回答

$y=−\frac{4}{5}x−5$

14。 用边界线写下图表所示的不等式$y=−x−3$。

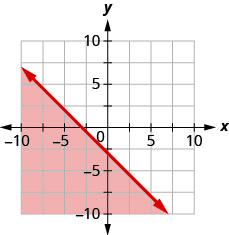
绘制每个线性不等式的图像。

15。 $y>\frac{3}{2}x+5$

回答

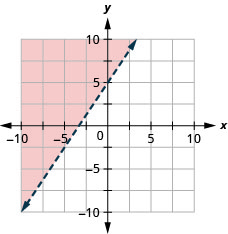
16。 $x−y\geq −4$

17。 $y\leq −5x$

回答

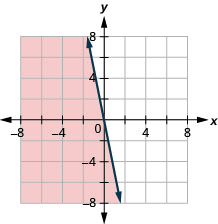
18。 Hiro 从事两份兼职工作，以便赚到足够的钱来履行每周至少450美元的义务。 她在购物中心的工作每小时支付10美元，而她在校园的行政助理工作每小时支付15美元。 Hiro 每份工作需要工作多少小时才能赚到至少 450 美元？

ⓐ 假设 x 是她在商场工作的小时数，让 y 成为她担任行政助理的小时数。 写一个不等式来模拟这种情况。
ⓑ 绘制不等式图。
ⓒ 找到三个可以解决$(x,y)$不等式的有序对。 然后解释一下这对Hiro意味着什么。

19。 使用这组有序对来 ⓐ 确定关系是否为函数，ⓑ 找到关系的域，ⓒ 找到关系的范围。

\ ({\ {(−3,27)、(−2,8)、(−1,1)、(0,0)、
(1,1)、(2,8)、(3,27)}\)

回答

ⓐ 是的 ⓑ${\{−3,−2,−1,0,1,2,3}\}$ ⓒ${\{0, 1, 8, 27}\}$

20。 评估函数：ⓐ$f(−1)$ ⓑ$f(2)$ ⓒ$f(c)$。

$f(x)=4x^2−2x−3$

21。 对于$h(y)=3|y−1|−3$，评估$h(−4)$。

回答

$12$

22。 确定图形是否是函数的图形。 解释你的答案。

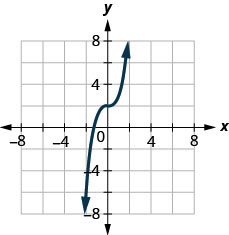
在以下练习中，ⓐ 绘制每个函数的图形 ⓑ 陈述其域和范围。
用间隔表示法写下域和范围。

23。 $f(x)=x^2+1$

回答

ⓐ

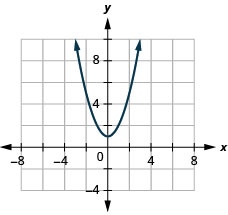
ⓑ$D: (-\inf ,\inf ), R: [1,\inf )$

24。 $f(x)=\sqrt{x+1}$

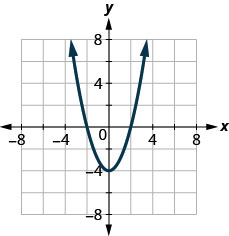
ⓑ 找到$y$-拦截。
ⓒ 查找$f(−1)$。
ⓓ 查找$f(1)$。
ⓔ 找到域名。 用间隔符号书写。
ⓕ 找到范围。 用间隔符号书写。

回答

ⓐ$x=−2,2$ ⓑ$y=−4$
ⓒ$f(−1)=−3$ ⓓ$f(1)=−3$
ⓔ$D: (-\inf ,\inf )$ ⓕ$R: [−4, \inf)$