3.7E:练习
- Page ID
- 203879
练习成就完美
使用垂直线测试
在以下练习中,确定每个图形是否是函数的图形。
1. ⓐ
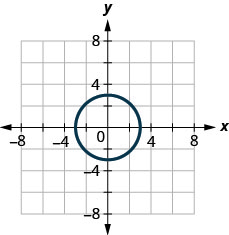
ⓑ
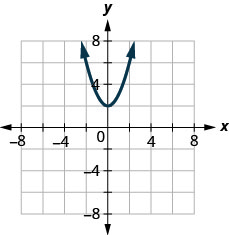
- 回答
-
ⓐ 不 ⓑ 是的
2. ⓐ
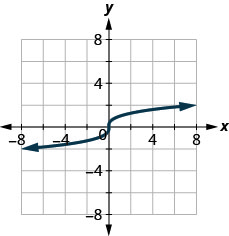
ⓑ
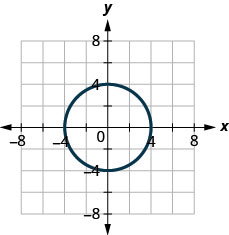
3. ⓐ
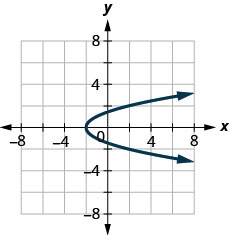
ⓑ
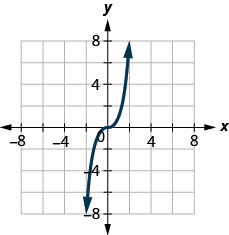
- 回答
-
ⓐ 不 ⓑ 是的
4. ⓐ
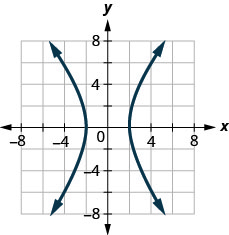
ⓑ
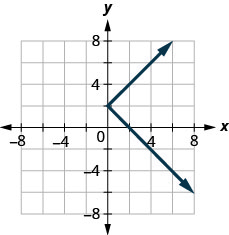
识别基本函数的图表
在以下练习中,ⓐ 绘制每个函数的图形 ⓑ 陈述其域和范围。 用间隔表示法写下域和范围。
5。 \(f(x)=3x+4\)
- 回答
-
ⓐ
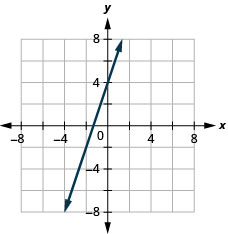
ⓑ\( D:(-\inf ,\inf ),\space R:(-\inf ,\inf ) \)
6。 \(f(x)=2x+5\)
7。 \(f(x)=−x−2\)
- 回答
-
ⓐ
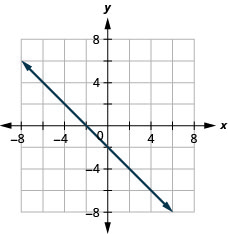
ⓑ\(D:(-\inf ,\inf ),\space R:(-\inf ,\inf )\)
8。 \(f(x)=−4x−3\)
9。 \(f(x)=−2x+2\)
- 回答
-
ⓐ
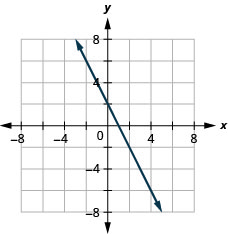
ⓑ\(D:(-\inf ,\inf ),\space R:(-\inf ,\inf )\)
10。 \(f(x)=−3x+3\)
11。 \(f(x)=\frac{1}{2}x+1\)
- 回答
-
ⓐ
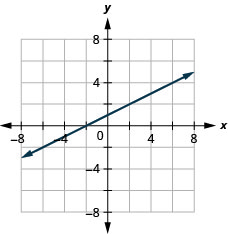
ⓑ\(D:(-\inf ,\inf ),\space R:(-\inf ,\inf )\)
12。 \(f(x)=\frac{2}{3}x−2\)
13。 \(f(x)=5\)
- 回答
-
ⓐ
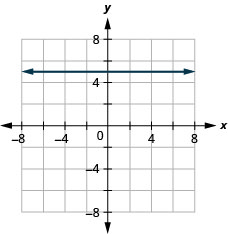
ⓑ\(D:(-\inf ,\inf ), R:{5}\)
14。 \(f(x)=2\)
15。 \(f(x)=−3\)
- 回答
-
ⓐ
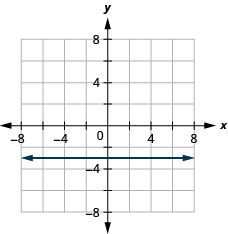
ⓑ\(D:(-\inf ,\inf ),\space R: {−3}\)
16。 \(f(x)=−1\)
17。 \(f(x)=2x\)
- 回答
-
ⓐ
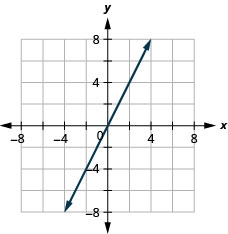
ⓑ\(D:(-\inf ,\inf ),\space R:(-\inf ,\inf )\)
18。 \(f(x)=3x\)
19。 \(f(x)=−2x\)
- 回答
-
ⓐ
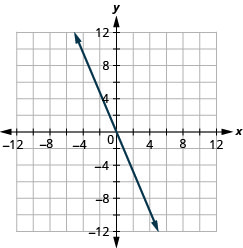
ⓑ\(D:(-\inf ,\inf ), R:(-\inf ,\inf )\)
20。 \(f(x)=−3x\)
21。 \(f(x)=3x^2\)
- 回答
-
ⓐ
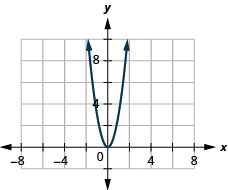
ⓑ\(D:(-\inf ,\inf ),\space R:[0,\inf )\)
22。 \(f(x)=2x^2\)
23。 \(f(x)=−3x^2\)
- 回答
-
ⓐ
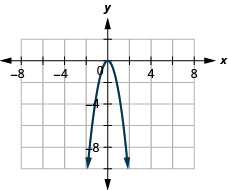
ⓑ\( D: (-\inf ,\inf ),\space R:(-\inf ,0]\)
24。 \(f(x)=−2x^2\)
25。 \(f(x)=12x^2\)
- 回答
-
ⓐ
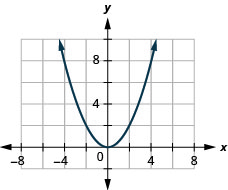
ⓑ\(D: (-\inf ,\inf ),\space R:[-\inf ,0)\)
26。 \(f(x)=\frac{1}{3}x^2\)
27。 \(f(x)=x^2−1\)
- 回答
-
ⓐ
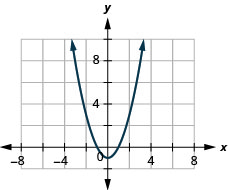
ⓑ\(D: (-\inf ,\inf ),\space R:[−1, \inf )\)
28。 \(f(x)=x^2+1\)
29。 \(f(x)=−2x^3\)
- 回答
-
ⓐ
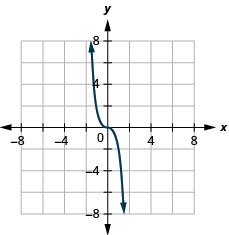
ⓑ\(D:(-\inf ,\inf ),\space R:(-\inf ,\inf )\)
30。 \(f(x)=2x^3\)
31。 \(f(x)=x^3+2\)
- 回答
-
ⓐ
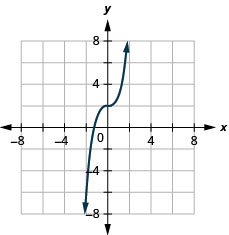
ⓑ\(D:(-\inf ,\inf ), R:(-\inf ,\inf )\)
32。 \(f(x)=x^3−2\)
33。 \(f(x)=2\sqrt{x}\)
- 回答
-
ⓐ
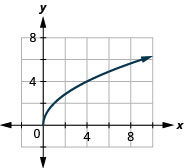
ⓑ\(D:[0,\inf ), R:[0,\inf )\)
34。 \(f(x)=−2\sqrt{x}\)
35。 \(f(x)=\sqrt{x-1}\)
- 回答
-
ⓐ
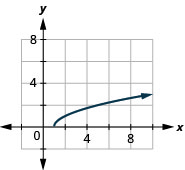
ⓑ\(D:[1,\inf ), R:[0,\inf )\)
36。 \(f(x)=\sqrt{x+1}\)
37。 \(f(x)=3|x|\)
- 回答
-
ⓐ
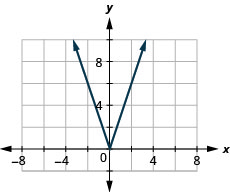
ⓑ\(D:[ −1,−1, \inf ), R:[−\inf ,\inf )\)
38。 \(f(x)=−2|x|\)
39。 \(f(x)=|x|+1\)
- 回答
-
ⓐ
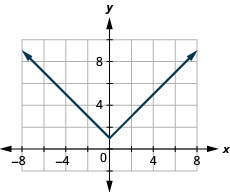
ⓑ\(D:(-\inf ,\inf ), R:[1,\inf )\)
40。 \(f(x)=|x|−1\)
从函数图中读取信息
在以下练习中,使用函数的图形来查找其域和范围。 用间隔表示法写下域和范围。
41。
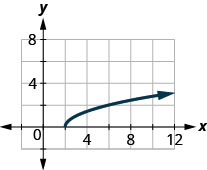
- 回答
-
\(D: [2,\inf ),\space R: [0,\inf )\)
42。
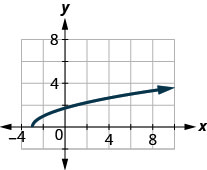
43。
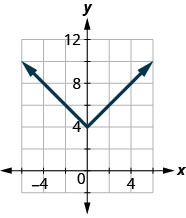
- 回答
-
\(D: (-\inf ,\inf ),\space R: [4,\inf )\)
44。
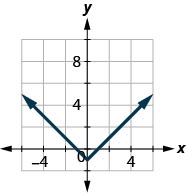
45。
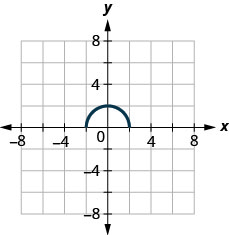
- 回答
-
\(D: [−2,2],\space R: [0, 2]\)
46。
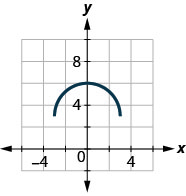
在以下练习中,使用函数的图形来查找指示的值。
47。
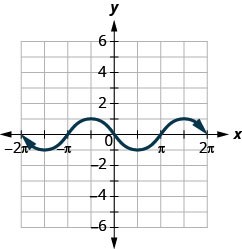
ⓐ 查找:\(f(0)\)。
ⓑ 查找:\(f(12\pi)\)。
ⓒ 查找:\(f(−32\pi)\)。
ⓓ 找出\(x\)何时的值\(f(x)=0\)。
ⓔ 找到\(x\)-拦截。
ⓕ 找到\(y\)-拦截。
ⓖ 找到域名。 用间隔符号书写。
ⓗ 找到范围。 用间隔符号书写。
- 回答
-
ⓐ\(f(0)=0\) ⓑ\((\pi/2)=−1\)
ⓒ\(f(−3\pi/2)=−1\) ⓓ f\(f(x)=0\) or\(x=−2\pi,-\pi,0,\pi,2\pi\)
ⓔ\((−2\pi,0),(−\pi,0),\)\((0,0),(\pi,0),(2\pi,0)\)\((f)(0,0)\)
ⓖ\([−2\pi,2\pi]\) ⓗ\([−1,1]\)
48。
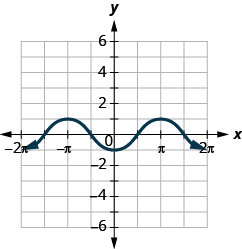
ⓐ 查找:\(f(0)\)。
ⓑ 查找:\(f(\pi)\)。
ⓒ 查找:\(f(−\pi)\)。
ⓓ 找出\(x\)何时的值\(f(x)=0\)。
ⓔ 找到\(x\)-拦截。
ⓕ 找到\(y\)-拦截。
ⓖ 找到域名。 用间隔符号书写。
ⓗ 找到范围。 用间隔符号书写
49。
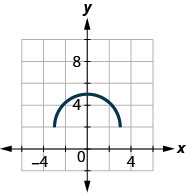
ⓐ 查找:\(f(0)\)。
ⓑ 查找:\(f(−3)\)。
ⓒ 查找:\(f(3)\)。
ⓓ 找出\(x\)何时的值\(f(x)=0\)。
ⓔ 找到\(x\)-拦截。
ⓕ 找到\(y\)-拦截。
ⓖ 找到域名。 用间隔符号书写。
ⓗ 找到范围。 用间隔符号书写。
- 回答
-
ⓐ\(f(0)=−6\) ⓑ\(f(−3)=3\) ⓒ\(f(3)=3\) ⓓ\(f(x)=0\) 不是 x ⓔ 没有 ⓕ\(y=6\) ⓖ\([−3,3]\)
ⓗ\([−3,6]\)
50。
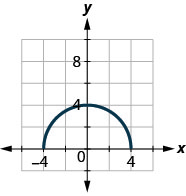
ⓐ 查找:\(f(0)\)。
ⓑ 找出\(x\)何时的值\(f(x)=0\)。
ⓒ 找到\(x\)-拦截。
ⓓ 找到\(y\)-拦截。
ⓔ 找到域名。 用间隔符号书写。
ⓕ 找到范围。 用间隔符号书写
写作练习
51。 用你自己的话解释如何从图中找到域。
52。 用你自己的话解释如何从图表中找到范围。
53。 用你自己的话解释如何使用垂直线测试。
54。 绘制正方形和立方体函数的草图。 图表中有哪些相似之处和不同之处?
自检
ⓐ 完成练习后,使用这份清单来评估你对本节目标的掌握程度。
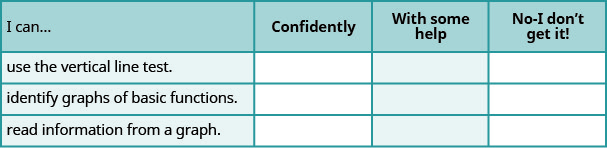
ⓑ 看完这份清单后,你会怎么做才能对所有目标充满信心?


