3.7: 函数图
- Page ID
- 203876
在本节结束时,您将能够:
- 使用垂直线测试
- 识别基本函数的图表
- 从函数图中读取信息
在开始之前,请参加这个准备测验。
使用垂直线测试
在上一节中,我们学习了如何确定关系是否为函数。 我们研究的关系以一组有序对、映射或方程来表示。 我们现在来看看如何分辨一个图表是否是函数的图形。
有序对\((x,y)\)是线性方程的解,前提是当有序对的 x 和 y 值被替换为方程时,该方程为真陈述。
线性方程的图形是一条直线,其中直线上的每个点都是方程的解,该方程的每个解都是这条线上的一个点。
在图中,我们可以看到,在方程图中\(y=2x−3\),每个 x 值只有一个 y 值,如附表所示。
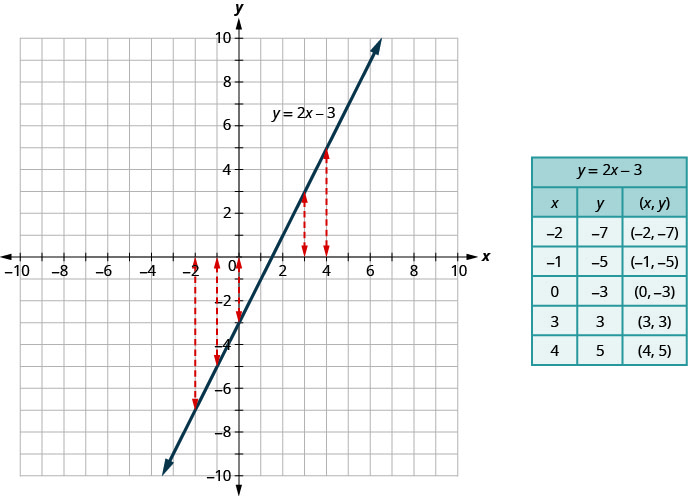
如果域中的每个元素在该范围内恰好有一个值,则关系就是一个函数。 因此,由方程定义的关系\(y=2x−3\)是一个函数。
如果我们看一下图表,每条垂直虚线仅在一个点处与直线相交。 这是有道理的,就像在函数中一样,每个 x 值都只有一个 y 值。
如果垂直线两次碰到图形,则 x 值将被映射到两个 y 值,因此该图不表示函数。
这将我们引向垂直线测试。 如果每条垂直线与图形最多相交一个点,则矩形坐标系中的一组点就是函数的图形。 如果有任何垂直线在多个点上与图形相交,则该图形不代表函数。
如果每条垂直线与图形最多相交一个点,则矩形坐标系中的一组点就是函数的图形。
如果有任何垂直线在多个点上与图形相交,则该图形不代表函数。
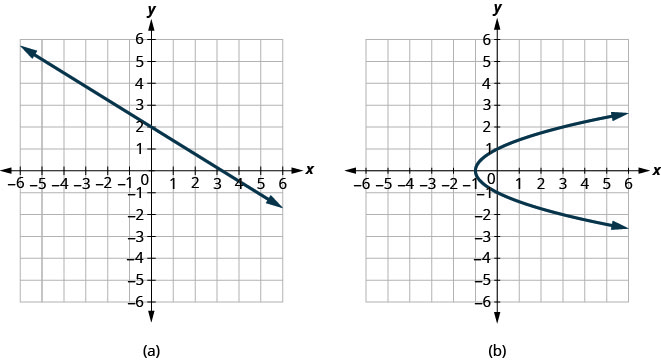
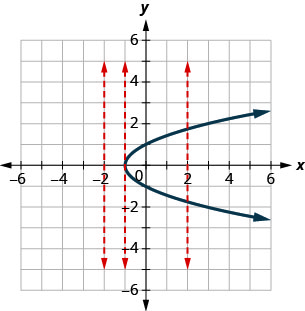
确定每个图形是否是函数的图形。
- 回答
-
ⓐ 由于任何垂直线最多与图形相交一个点,因此该图形是函数的图形。
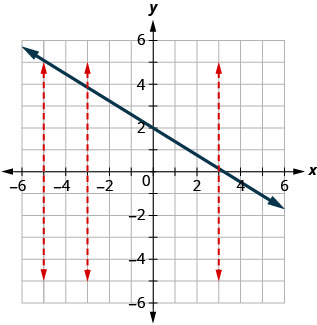
ⓑ 图表上显示的一条垂直线将其交叉成两点。 此图不代表函数。
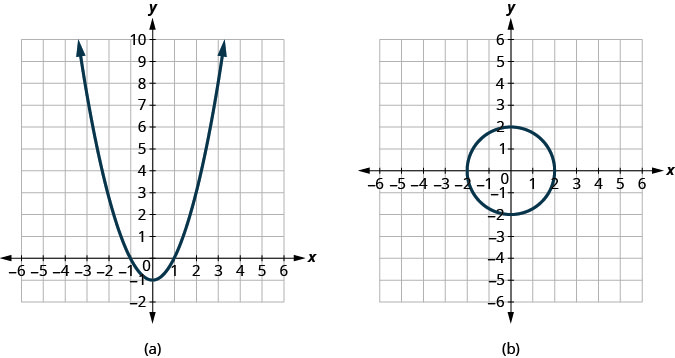
确定每个图形是否是函数的图形。
- 回答
-
ⓐ 是的 ⓑ 不
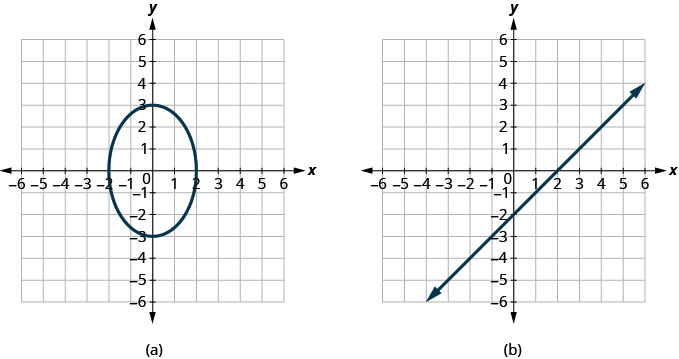
确定每个图形是否是函数的图形。
- 回答
-
ⓐ 不 ⓑ 是的
识别基本函数的图表
我们在开发垂直线测试时使用了方程\(y=2x−3\)及其图形。 我们说方程定义的关系\(y=2x−3\)是一个函数。
我们可以将其写成函数表示法\(f(x)=2x−3\)。 它仍然意味着同样的事情。 函数的图形是所有有序对的图形,\((x,y)\)其中\(y=f(x)\)。 因此,我们可以将有序对写为\((x,f(x))\)。 看起来不一样,但图表会是一样的。
将\(y=2x−3\)先前在图中所示的图形与图\(f(x)=2x−3\)中所示的图表进行比较。 除了符号之外什么都没有改变。
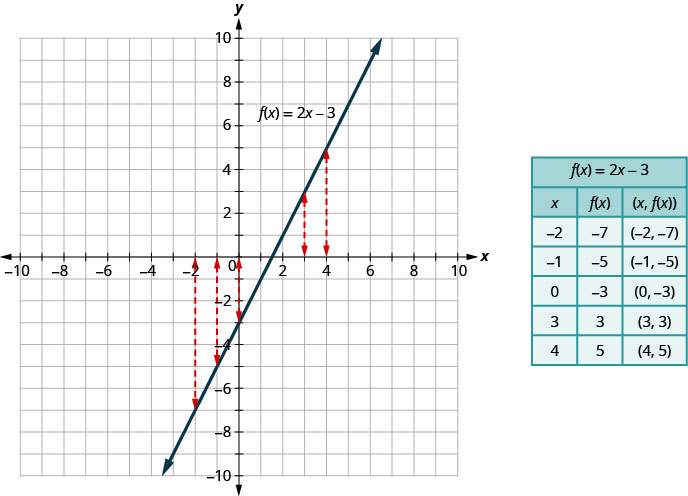
函数的图是其所有有序对的图形,即 (x, y) (x, y) 或使用函数表示法 (x, f (x)) (x, f (x)),其中 y=f (x) .y=f (x)。
\[\begin{array} {ll} {f} &{\text{name of function}} \\ {x} &{\text{x-coordinate of the ordered pair}} \\ {f(x)} &{\text{y-coordinate of the ordered pair}} \\ \nonumber \end{array}\]
随着我们的研究向前推进,熟悉几个基本函数的图表并能够识别它们会很有帮助。
通过我们之前的工作,我们已经熟悉了线性方程的图形。 我们用来决定\(y=2x−3\)是否为函数的过程将适用于所有线性方程。 所有非垂直线性方程都是函数。 垂直线不是函数,因为 x 值有无限多的 y 值。
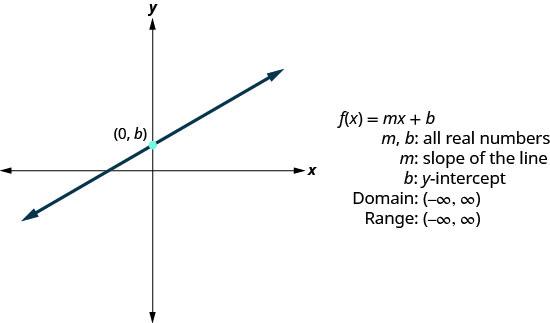
我们用几种形式编写了线性方程,但是使用线性方程的斜率截距形式对我们最有帮助。 线性方程的斜率截距形式为\(y=mx+b\)。 在函数表示法中,此线性函数变为其\(f(x)=mx+b\)中 m 是直线的斜率,b 是 y 截距。
域是所有实数的集合,范围也是所有实数的集合。
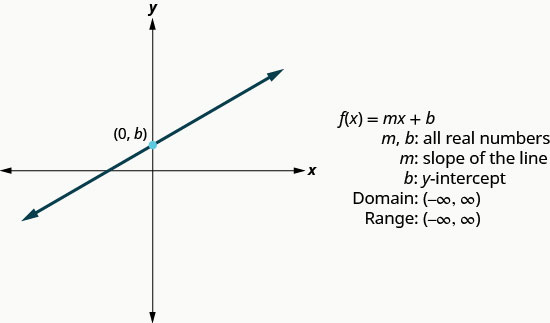
我们将使用之前使用的绘图技术来绘制基本函数。
图:\(f(x)=−2x−4\)。
- 回答
-
\(f(x)=−2x−4\) 我们认为这是一个线性函数。 找出斜率和 y 截距。 \(m=−2\)
\(b=−4\)使用斜率截距绘制图形。 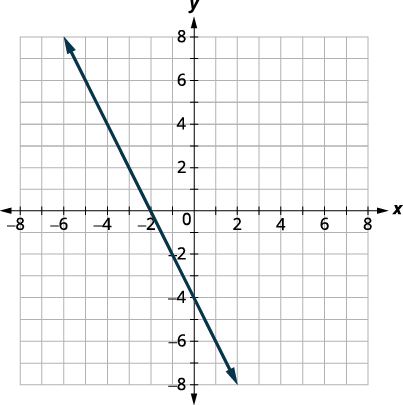
图表:\(f(x)=−3x−1\)
- 回答
-
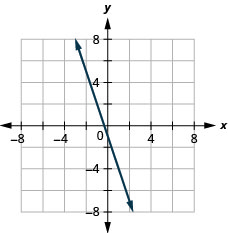
图表:\(f(x)=−4x−5\)
- 回答
-
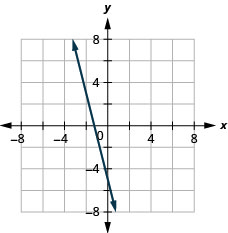
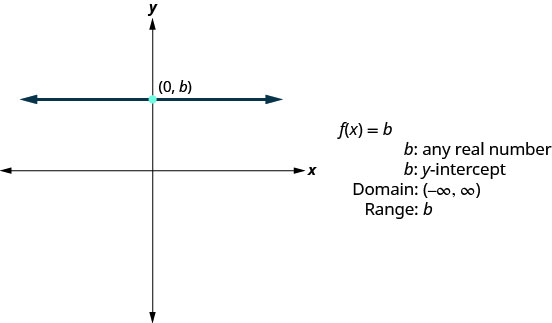
我们将要看其图形的下一个函数称为常量函数,其方程的形式为\(f(x)=b\),其中 b 是任意实数。 如果我们用 y\(f(x)\) 替换,我们得到\(y=b\)。 我们认为这是一条水平线,其 y 截距为 b。 函数\(f(x)=b\)的图形也是 y 截距为 b 的水平线。
请注意,对于我们在函数中输入的任何实数,函数值都将为 b。 这告诉我们该范围只有一个值 b。
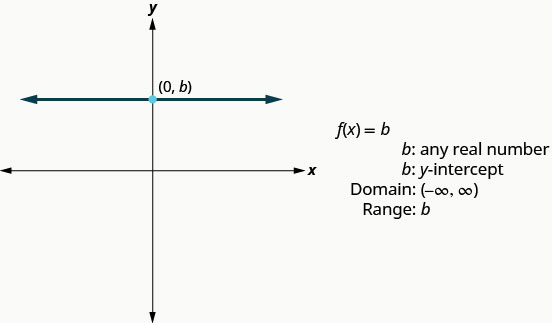
图:\(f(x)=4\)。
- 回答
-
\(f(x)=4\) 我们认为这是一个常量函数。 该图将是一条水平线\((0,4)\)。 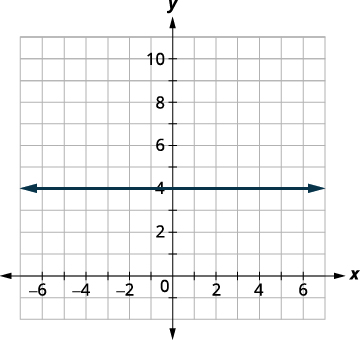
图:\(f(x)=−2\)。
- 回答
-
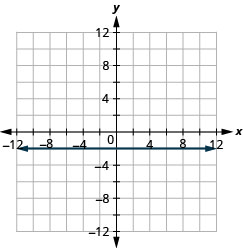
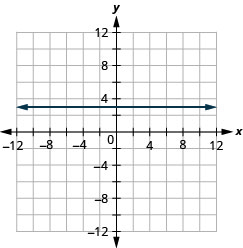
图:\(f(x)=3\)。
- 回答
-
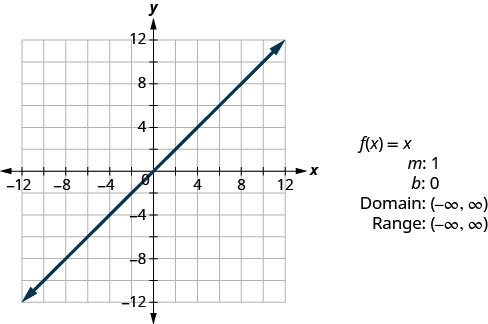
恒等函数\(f(x)=x\)是线性函数的特例。 如果我们用线性函数的形式写出来\(f(x)=1x+0\),则会看到斜率为 1,y 截距为 0。
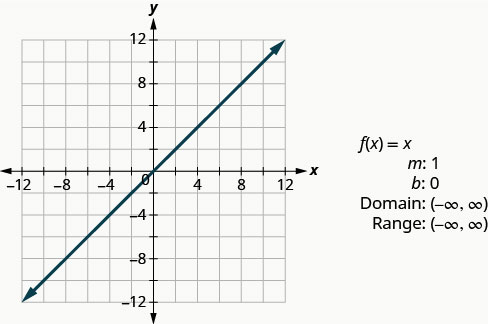
我们要看的下一个函数不是线性函数。 因此,图表不会是一条线。 我们绘制此函数图表的唯一方法是点绘图。 因为这是一个不熟悉的函数,所以我们一定要为我们的 x 值选择几个正负值以及 0。
图:\(f(x)=x^2\)。
- 回答
-
我们选择 x 值。 我们在中替换它们,然后创建图表,如图所示。
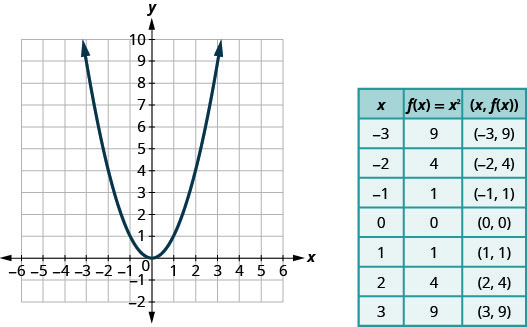
图:\(f(x)=x^2\)。
- 回答
-
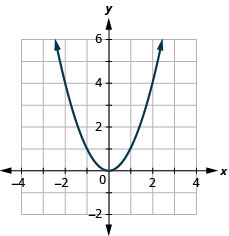
\(f(x)=−x^2\)
- 回答
-
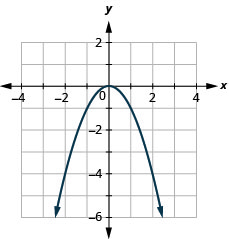
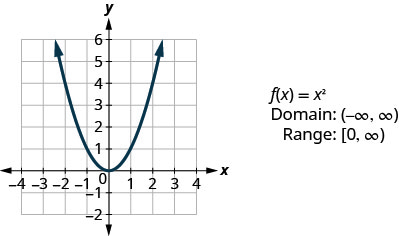
看看示例中的结果,我们可以总结方函数的特征。 我们称这张图为抛物线。 在我们考虑域时,请注意任何实数都可以用作 x 值。 域名全部为实数。
范围不全是实数。 请注意,该图由 y 的值组成,切勿低于零。 这是有道理的,因为任何数字的平方都不能为负数。 因此,平方函数的范围都是非负实数。
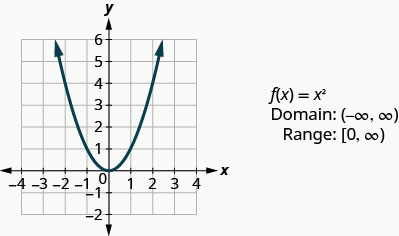
我们要看的下一个函数也不是线性函数,所以图形不会是直线。 同样,我们将使用点图,并确保为我们的 x 值选择几个正负值以及 0。
图:\(f(x)=x^3\)。
- 回答
-
我们选择 x 值。 我们用它们代替,然后创建图表。
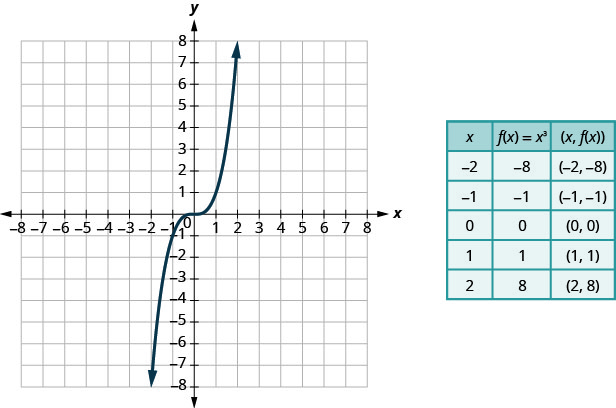
图:\(f(x)=x^3\)。
- 回答
-
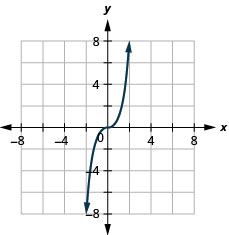
图:\(f(x)=−x^3\)。
- 回答
-
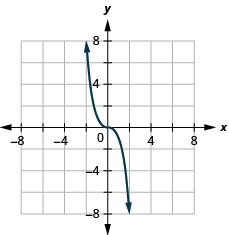
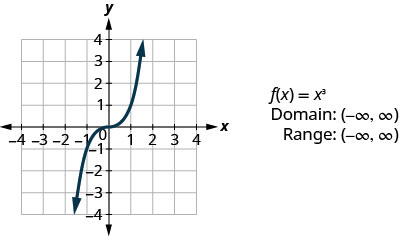
查看示例中的结果,我们可以总结立方体函数的特征。 在我们考虑域时,请注意任何实数都可以用作 x 值。 域名全部为实数。
范围均为实数。 这是有道理的,因为任何非零数的立方体都可以是正数或负数。 因此,立方体函数的范围都是实数。
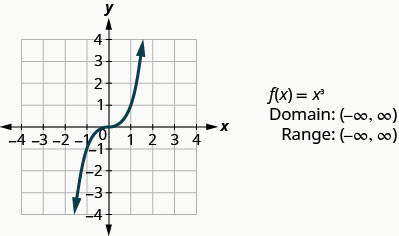
我们要看的下一个函数不是对输入值求平方或立方体,而是取这些值的平方根。
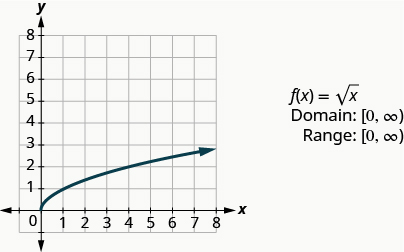
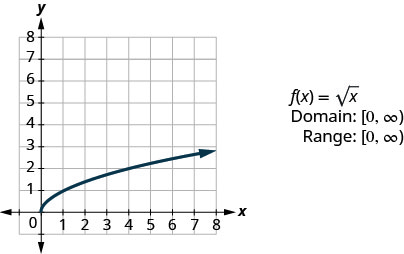
让我们绘制函数的图表,\(f(x)=\sqrt{x}\)然后总结函数的特征。 请记住,我们只能取非负实数的平方根,所以我们的域将是非负实数。
\(f(x)=\sqrt{x}\)
- 回答
-
我们选择 x 值。 由于我们将取平方根,因此我们选择完美平方的数字,以便于我们的工作。 我们用它们代替,然后创建图表。
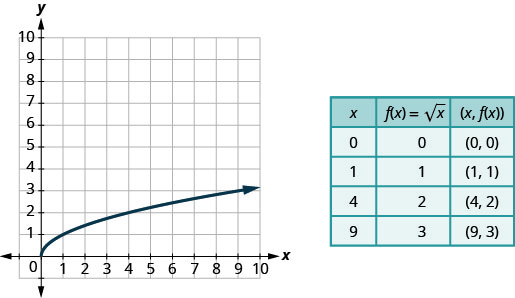
图:\(f(x)=x\)。
- 回答
-
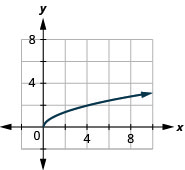
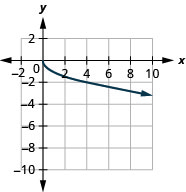
图:\(f(x)=−\sqrt{x}\)。
- 回答
-
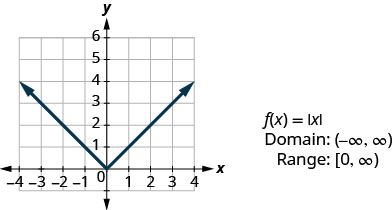
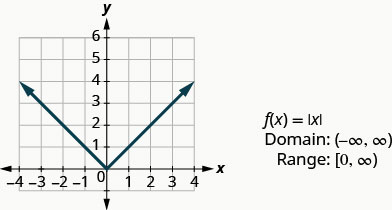
我们的最后一个基本函数是绝对值函数\(f(x)=|x|\)。 请记住,一个数字的绝对值是它与零的距离。 由于我们从不用负数来测量距离,因此我们永远不会得到该范围内的负数。
图:\(f(x)=|x|\)。
- 回答
-
我们选择 x 值。 我们用它们代替,然后创建图表。
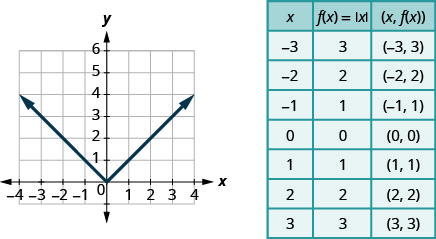
图:\(f(x)=|x|\)。
- 回答
-
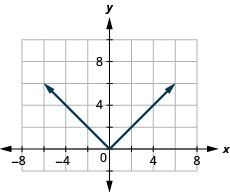
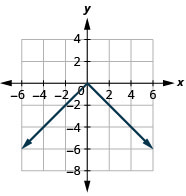
图:\(f(x)=−|x|\)。
- 回答
-
从函数图中读取信息
在科学和商业领域,通常收集数据,然后绘制图表。 对图表进行分析,从图表中获取信息,然后通常根据数据进行预测。
首先,我们将从函数的图中读取函数的域和范围。
请记住,域是函数中有序对中所有 x 值的集合。 为了找到域,我们查看图形并找出图形上具有相应值的所有 x 值。 垂直跟随值 x 向上或向下。 如果你点击函数的图形,那么 x 就在域中。
请记住,范围是函数中有序对中所有 y 值的集合。 为了找到范围,我们看一下图形,找出图形上所有具有相应值的 y 值。 水平跟随值 y 向左或向右。 如果你点击函数的图形,那么 y 就在范围内。
使用函数的图形来查找其域和范围。 用间隔表示法写下域和范围。
![此图在 x y 坐标平面上绘制了一条曲线段。 x 轴从负 4 延伸到 4。 y 轴从负 4 延伸到 4。 曲线段穿过点(负 3、负 1)、(1.5、3)和(3、1)。 间隔 [负 3, 3] 标记在水平轴上。 间隔 [负 1, 3] 标记在垂直轴上。](https://math.libretexts.org/@api/deki/files/22958/CNX_IntAlg_Figure_03_06_021_img_new.jpg)
- 回答
-
为了找到域,我们查看图形并找到与图上某个点对应的所有 x 值。 该域在图表上以红色突出显示。 域是\([−3,3]\)。
为了找到范围,我们看一下图形并找到与图上某个点对应的所有 y 值。 该范围在图表上以蓝色突出显示。 范围是\([−1,3]\)。
使用函数的图形来查找其域和范围。 用间隔表示法写下域和范围。
![此图在 x y 坐标平面上绘制了一条曲线段。 x 轴从负 6 延伸到 6。 y 轴从负 6 延伸到 6。 曲线段穿过点(负 5、负 4)、(0、负 3)和(1、2)。 间隔 [负 5, 1] 标记在水平轴上。 间隔 [负 4, 2] 标记在垂直轴上。](https://math.libretexts.org/@api/deki/files/22776/CNX_IntAlg_Figure_03_06_022_img_new.jpg)
- 回答
-
域是\([−5,1]\)。 范围是\([−4,2]\)。
使用函数的图形来查找其域和范围。 用间隔表示法写下域和范围。
![此图在 x y 坐标平面上绘制了一条曲线段。 x 轴从负 4 到 5 延伸。 y 轴从负 6 延伸到 4。 曲线段穿过点(负 2、1)、(0、3)和(4、负 5)。 间隔 [负 2, 4] 标记在水平轴上。 间隔 [负 5, 3] 标记在垂直轴上。](https://math.libretexts.org/@api/deki/files/22921/CNX_IntAlg_Figure_03_06_023_img_new.jpg)
- 回答
-
域是\([−2,4]\)。 范围是\([−5,3]\)。
我们现在要从图表中读取你可能在以后的数学课中看到的信息。
使用函数的图形来查找指示的值。

ⓐ 查找:\(f(0)\)。
ⓑ 查找:\(f(32\pi)\)。
ⓒ 查找:\(f(−12\pi)\)。
ⓓ 在什么时候找出 x 的值\(f(x)=0\)。
ⓔ 找到 x 截取。
ⓕ 找到 y 截取。
ⓖ 找到域名。 用间隔符号书写。
ⓗ 找到范围。 用间隔符号书写。
- 回答
-
ⓐ 当\(x=0\),函数在 0 处穿过 y 轴。 所以,\(f(0)=0\)。
ⓑ 当\(x=32\pi\),函数的 y 值为\(−1\)。 所以,\(f(32\pi)=−1\)。
ⓒ 当\(x=−12\pi\),函数的 y 值为\(−1\)。 所以,\(f(−12\pi)=−1\)。
ⓓ 该函数在点处为 0\((−2\pi,0), (−\pi,0), (0,0),(\pi,0),(2\pi,0)\)。 如果\(f(x)=0\)是,则为 x 值\(−2\pi,−\pi,0,\pi,2\pi\)。
ⓔ x 截获发生在\(y=0\). 所以 x-截获发生在什么时候\(f(x)=0\)。 x-interce pts 是\((−2\pi,0),(−\pi,0),(0,0),(\pi,0),(2\pi,0)\)。
ⓕ y 截获发生在 x=0.x=0 时。 因此 y 截获发生在\(f(0)\)。 y 截距为\((0,0)\)。
ⓖ 当 x 为从\(−2\pi\)到时,此函数具有一个值\(2\pi\)。 因此,区间表示法中的域为\([−2\pi,2\pi]\)。
ⓗ 此函数值或 y 值从\(−1\)到 1。 因此,以间隔表示法表示的范围为\([−1,1]\)。
使用函数的图形来查找指示的值。
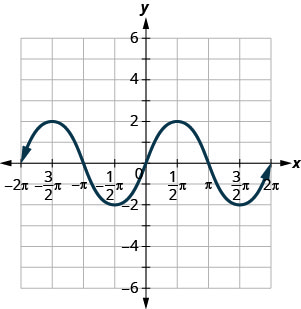
ⓐ 查找:f (0) .f (0)。
ⓑ 查找:f (12\ pi) .f (12\ pi)。
ⓒ 查找:f (−32\ pi) .f (−32\ pi)。
ⓓ 在 f (x) =0.f (x) =0 时找出 x 的值。
ⓔ 找到 x 截取。
ⓕ 找到 y 截取。
ⓖ 找到域名。 用间隔符号书写。
ⓗ 找到范围。 用间隔符号书写。
- 回答
-
ⓐ\(f(0)=0\) ⓑ\(f=(\pi2)=2\) ⓒ\(f=(−3\pi2)=2\) ⓓ f\(f(x)=0\) or\(x=−2\pi,−\pi,0,\pi,2\pi\) ⓔ\((−2\pi,0),(−\pi,0),(0,0),(\pi,0),(2\pi,0)\) ⓕ (0,0) (0,0) ⓖ\([−2\pi,2\pi]\) ⓗ\([−2,2]\)
使用函数的图形来查找指示的值。
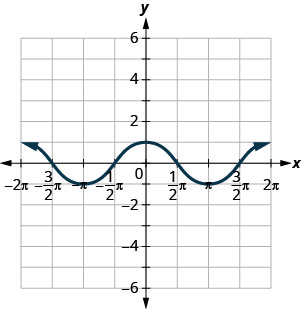
ⓐ 查找:\(f(0)\)。
ⓑ 查找:\(f(\pi)\)。
ⓒ 查找:\(f(−\pi)\)。
ⓓ 在什么时候找出 x 的值\(f(x)=0\)。
ⓔ 找到 x 截取。
ⓕ 找到 y 截取。
ⓖ 找到域名。 用间隔符号书写。
ⓗ 找到范围。 用间隔符号书写。
- 回答
-
ⓐ\(f(0)=1\) ⓑ\(f(\pi)=−1\) ⓒ\(f(−\pi)=−1\) ⓓ f\(f(x)=0\) or\(x=−3\pi2,−\pi2,\pi2,3\pi2\) ⓔ\((−2pi,0),(−pi,0),(0,0),(pi,0),(2pi,0)\) ⓕ\((0,1)\) ⓖ\([−2pi,2pi]\) ⓗ\([−1,1]\)
访问此在线资源以获取更多指导和使用函数图表进行练习。
关键概念
- 垂直线测试
- 如果每条垂直线与图形最多相交一个点,则矩形坐标系中的一组点就是函数的图形。
- 如果有任何垂直线在多个点上与图形相交,则该图形不代表函数。
- 函数图
- 函数的图是其所有有序对的图形,即 (x, y) (x, y) 或使用函数表示法 (x, f (x)) (x, f (x)),其中 y=f (x) .y=f (x)。
fxf (x) 有序对坐标的 functionx-corident 的名称 functionxx-corident 的有序对坐标的名称 functionxx-corident
- 函数的图是其所有有序对的图形,即 (x, y) (x, y) 或使用函数表示法 (x, f (x)) (x, f (x)),其中 y=f (x) .y=f (x)。
- 线性函数
- 常量函数
- 身份函数
- 方形函数
- 立方体函数
- 平方根函数
- 绝对值函数