3.6E:练习
- Page ID
- 203878
练习成就完美
找出关系的域和范围
在以下练习中,对于每个关系 a. 找出关系域 b. 找出关系的范围。
1。 \({\{(1,4),(2,8),(3,12),(4,16),(5,20)}\}\)
- 回答
-
a.\({\{1, 2, 3, 4, 5}\}\) b。\({\{4, 8, 12, 16, 20}\}\)
2。 \({\{(1,−2),(2,−4),(3,−6),(4,−8),(5,−10)}\}\)
3。 \({\{(1,7),(5,3),(7,9),(−2,−3),(−2,8)}\}\)
- 回答
-
a.\({\{1, 5, 7, −2}\}\) b。\({\{7, 3, 9, −3, 8}\}\)
4。 \({\{(11,3),(−2,−7),(4,−8),(4,17),(−6,9)}\}\)
在以下练习中,使用关系映射到 a. 列出关系的有序对,b. 找到关系的域,c. 找出关系的范围。
5。

- 回答
-
a.(丽贝卡,1 月 18 日),(詹妮弗,4 月 1 日),(约翰,1 月 18 日),(赫克托,6 月 23 日),(路易斯,2 月 15 日),(拉斐尔,11 月 6 日),(梅雷迪思,8 月 19 日),(约瑟夫,7 月 30 日)
b. {丽贝卡、詹妮弗、约翰、赫克托、路易斯、乌木,拉斐尔、梅雷迪思、凯伦、约瑟夫}
c. {1 月 18 日、4 月 1 日、6 月 23 日、2 月 15 日、4 月 7 日、11 月 6 日、8 月 19 日、7 月 30 日}
6。

7。 对于身高女性\(5'4''\),下图显示了相应的身体质量指数(BMI)。 体重指数是根据身高和体重来衡量体内脂肪的指标。 体重指数为被认为\(18.5–24.9\)是健康的。
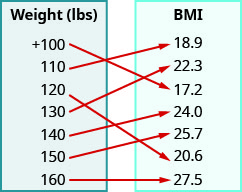
- 回答
-
a.\((+100, 17. 2), (110, 18.9), (120, 20.6), (130, 22.3), (140, 24.0), (150, 25.7), (160, 27.5)\) b.\({\{+100, 110, 120, 130, 140, 150, 160,}\}\) c.\({\{17.2, 18.9, 20.6, 22.3, 24.0, 25.7, 27.5}\}\)
8。 对于身高的人,\(5'11''\)下图显示了相应的身体质量指数(BMI)。 体重指数是根据身高和体重来衡量体内脂肪的指标。 体重指数为被认为\(18.5–24.9\)是健康的。
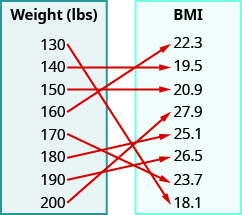
在以下练习中,使用关系图 a. 列出关系的有序对 b. 找到关系的域 c. 找到关系的范围。
9。
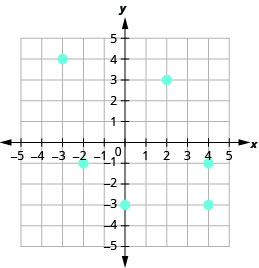
- 回答
-
a.\((2, 3), (4, −3), (−2, −1), (−3, 4), (4, −1), (0, −3)\) b.\({\{−3, −2, 0, 2, 4}\}\)
c.\({\{−3, −1, 3, 4}\}\)
10。
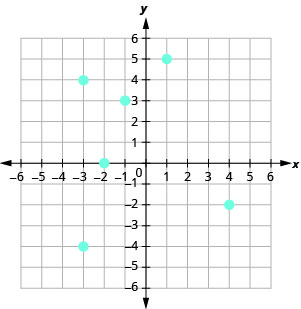
11。
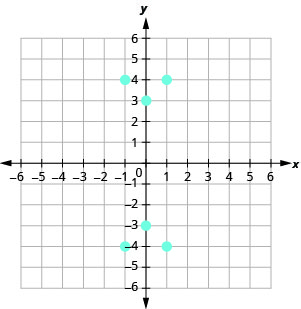
- 回答
-
a.\((1, 4), (1, −4), (−1, 4), (−1, −4), (0, 3), (0, −3)\) b.\({\{−1, 0, 1}\}\) c.\({\{−4, −3, 3,4}\}\)
12。
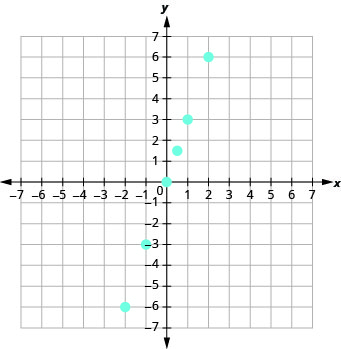
确定关系是否为函数
在以下练习中,使用一组有序对来 a. 确定关系是否为函数,b. 找到关系的域,c. 找出关系的范围。
13。 \( {\{(−3,9),(−2,4),(−1,1), (0,0),(1,1),(2,4),(3,9)}\}\)
- 回答
-
a. 是的 b.\({\{−3, −2, −1, 0, 1, 2, 3}\}\) c.\({\{9, 4, 1, 0}\}\)
14。 \({\{(9,−3),(4,−2),(1,−1),(0,0),(1,1),(4,2),(9,3)}\}\)
15。 \({\{(−3,27),(−2,8),(−1,1), (0,0),(1,1),(2,8),(3,27)}\}\)
- 回答
-
a. 是的 b.\({\{−3, −2, −1, 0, 1, 2, 3}\}\) c.\({\{0, 1, 8, 27}\}\)
16。 \({\{(−3,−27),(−2,−8),(−1,−1), (0,0),(1,1),(2,8),(3,27)}\}\)
在以下练习中,使用映射到 a. 确定关系是否为函数,b. 找到函数的域,c. 找出函数的范围。
17。
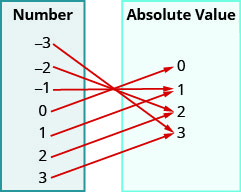
- 回答
-
a. 是的 b.\({\{−3, −2, −1, 0, 1, 2, 3}\}\) c.\({\{0, 1, 2, 3}\}\)
18。
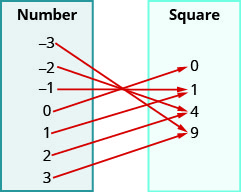
19。

- 回答
-
a.no b。{Jenny、R and y、Dennis、Emily、Raul} c. {rHern 和 ez@state.edu,JKim@gmail.com,Raul@gmail.com ESmith@state.edu DBroen@aol.com jenny@aol.cvom,R 和mailto:y@gmail.com} y@gmail.com
20。

在以下练习中,确定每个方程是否为函数。
21. a.\(2x+y=−3\)
b.\(y=x^2\)
c.\(x+y^2=−5\)
- 回答
-
a. 是的 b. 是的 c. 不
22. a.\(y=3x−5\)
b.\(y=x^3\)
c.\(2x+y^2=4\)
23. a.\(y−3x^3=2\)
b.\(x+y^2=3\)
c.\(3x−2y=6\)
- 回答
-
a. 是的 b. 不 c. 是的
24. a.\(2x−4y=8\)
b.\(−4=x^2−y\)
c.\(y^2=−x+5\)
找出一个函数的值
在以下练习中,评估函数:a.\(f(2)\) b.\(f(−1)\) c\(f(a)\).
25。 \(f(x)=5x−3\)
- 回答
-
a.\(f(2)=7\) b.\(f(−1)=−8\) c.\(f(a)=5a−3\)
26。 \(f(x)=3x+4\)
27。 \(f(x)=−4x+2\)
- 回答
-
a.\(f(2)=−6\) b.\(f(−1)=6\) c.\(f(a)=−4a+2\)
28。 \(f(x)=−6x−3\)
29。 \(f(x)=x^2−x+3\)
- 回答
-
a.\(f(2)=5\) b.\(f(−1)=5\)
c.\(f(a)=a^2−a+3\)
30。 \(f(x)=x^2+x−2\)
31。 \(f(x)=2x^2−x+3\)
- 回答
-
a.\(f(2)=9\) b.\(f(−1)=6\)
c.\(f(a)=2a^2−a+3\)
32。 \(f(x)=3x^2+x−2\)
在以下练习中,评估函数:a.\(g(h^2)\) b.\(g(x+2)\) c\(g(x)+g(2)\).
33。 \(g(x)=2x+1\)
- 回答
-
a.\(g(h^2)=2h^2+1\)
b.\(g(x+2)=4x+5\)
c.\(g(x)+g(2)=2x+6\)
34。 \(g(x)=5x−8\)
35。 \(g(x)=−3x−2\)
- 回答
-
a.\(g(h^2)=−3h^2−2\)
b.\(g(x+2)=−3x−8\)
c.\(g(x)+g(2)=−3x−10\)
36。 \(g(x)=−8x+2\)
37。 \(g(x)=3−x\)
- 回答
-
a.\(g(h^2)=3−h^2\)
b.\(g(x+2)=1−x\)
c.\(g(x)+g(2)=4−x\)
38。 \(g(x)=7−5x\)
在以下练习中,评估该函数。
39。 \(f(x)=3x^2−5x\);\(f(2)\)
- 回答
-
2
40。 \(g(x)=4x^2−3x\);\(g(3)\)
41。 \(F(x)=2x^2−3x+1\);\(F(−1)\)
- 回答
-
6
42。 \(G(x)=3x^2−5x+2\);\(G(−2)\)
43。 \(h(t)=2|t−5|+4\);\(f(−4)\)
- 回答
-
22
44。 \(h(y)=3|y−1|−3\);\(h(−4)\)
45。 \(f(x)=x+2x−1\);\(f(2)\)
- 回答
-
4
46。 \(g(x)=x−2x+2\);\(g(4)\)
在以下练习中,求解。
47。 西尔维亚的DVR中未观看的节目数量为85个。 这个数字每周增加20个未观看的节目。 该函数\(N(t)=85+20t\)表示未观看节目的数量 N 与时间 t(以周为单位)之间的关系。
a. 确定自变量和因变量。
b. 查找\(N(4)\)。 解释这个结果是什么意思
- 回答
-
a. t IND; N DEP
b.\(N(4)=165\) 第四周西尔维亚的 DVR 中未观看的节目数量。
48。 每天都会在 Ken 的账户中下载一个新的拼图。 现在他的账户里有 43 个谜题。 该函数\(N(t)=43+t\)表示拼图数量 N 和时间 t 之间的关系,以天为单位。
a. 确定自变量和因变量。
b. 查找\(N(30)\)。 解释这个结果是什么意思。
49。 印刷公司印刷一本书的每日成本由函数建模,其\(C(x)=3.25x+1500\)中 C 是每日总成本,x 是印刷的书籍数量。
a. 确定自变量和因变量。
b. 查找\(N(0)\)。 解释这个结果是什么意思。
c. 查找\(N(1000)\)。 解释这个结果是什么意思。
- 回答
-
a. x IND; C DEP
b.\(N(0)=1500\) 不印刷书籍时的每日成本
c.\(N(1000)=4750\) 印刷 1000 本书的每日成本
50。 制造公司的每日成本由函数建模,\(C(x)=7.25x+2500\)其中\(C(x)\)是每日总成本,x 是制造的物品数量。
a. 确定自变量和因变量。
b. 查找\(C(0)\)。 解释这个结果是什么意思。
c. 查找\(C(1000)\)。 解释这个结果是什么意思。
写作练习
51。 用你自己的话说,解释关系和函数之间的区别。
52。 用你自己的话说,解释域和范围的含义。
53。 每个关系都是函数吗? 每个函数都是关系吗?
54。 你如何找到一个函数的值?
自检
a. 完成练习后,使用此清单评估您对本节目标的掌握程度。
b. 看完清单后,你认为你为下一节做好了充分的准备吗? 为什么或者为什么不呢?


