3.6: 关系和函数

学习目标

在本节结束时，您将能够：

• 找出关系的域和范围
• 确定关系是否为函数
• 找出一个函数的值

在开始之前，请参加这个准备测验。

1. 评估\(3x−5\)时间\(x=−2\)。
   如果你错过了这个问题，请查看 [链接]。
2. 评估\(2x^2−x−3\)时间\(x=a\)。
   如果你错过了这个问题，请查看 [链接]。
3. 简化：\(7x−1−4x+5\)。
   如果你错过了这个问题，请查看 [链接]。

找出关系的域和范围

在我们日常生活中，我们有许多与我们的名字配对的数据项或数量。 我们的社会保险号、学生证号码、电子邮件地址、电话号码和我们的生日都与我们的姓名相匹配。 我们的名字和每件物品之间都有关系。

当你的教授拿到她的班级名册时，该班所有学生的姓名将列在一列中，然后学生证号码很可能出现在下一列中。 如果我们将对应关系视为一组有序对，其中第一个元素是学生姓名，第二个元素是学生的身份证号，我们称之为关系。

\[(\text{Student name}, \text{ Student ID #})\nonumber \]

班级中所有学生姓名的集合称为关系域，与这些学生配对的所有学生证号码的集合是关系的范围。

在许多类似的情况下，一个变量与另一个变量配对或匹配。 记录此匹配的有序对集合是一种关系。

定义：关系

关系是任何一组有序对\((x,y)\)。 有序对中的所有 x 值共同构成了域。 有序对中的所有 y 值共同构成了范围。

示例\(\PageIndex{1}\)

对于关系\({(1,1),(2,4),(3,9),(4,16),(5,25)}\)：

1. 找到关系域。
2. 找出关系的范围。

回答

\[\begin{array} {ll} {} &{ {\{(1,1), (2,4), (3,9), (4,16), (5,25) }\} } \\ {ⓐ\text{ The domain is the set of all x-values of the relation.}} &{ {\{1,2,3,4,5}\} } \\ {ⓑ\text{ The range is the set of all y-values of the relation.}} &{ {\{1,4,9,16,25}\} } \\ \nonumber \end{array}\]

示例\(\PageIndex{2}\)

对于关系\({\{(1,1),(2,8),(3,27),(4,64),(5,125)}\}\)：

1. 找到关系域。
2. 找出关系的范围。

回答 a

\({\{1,2,3,4,5}\}\)

答案 b

\({\{1,8,27,64,125}\}\)

示例\(\PageIndex{3}\)

对于关系\({\{(1,3),(2,6),(3,9),(4,12),(5,15)}\}\)：

1. 找到关系域。
2. 找出关系的范围。

回答 a

\({\{1,2,3,4,5}\}\)

答案 b

\({\{3,6,9,12,15}\}\)

映射

映射有时用于显示关系。 箭头显示域元素与范围元素的配对。

示例\(\PageIndex{4}\)

使用显示的关系映射来

1. 列出关系的有序对，
2. 找到关系的域，然后
3. 找到关系的范围。

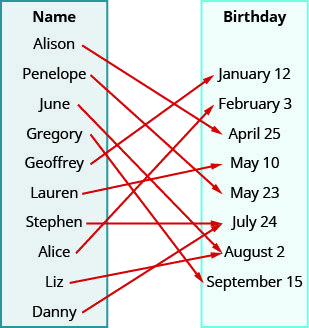
回答

ⓐ 箭头显示此人与其生日的匹配情况。 我们创建有序对，将人的名字作为 x 值，他们的生日作为 y 值。

{（艾莉森，4 月 25 日），（佩内洛普，5 月 23 日），（格雷戈里，9 月 15 日），（杰弗里，1 月 12 日），（劳伦，5 月 10 日），（斯蒂芬，7 月 24 日），（丽兹，8 月 24 日），（丹尼，7 月 24 日）}

ⓑ 该域是关系的所有 x 值的集合。

{艾莉森、佩内洛普、六月、格雷戈里、杰弗里、劳伦、斯蒂芬、爱丽丝、丽兹、丹尼}

ⓒ 范围是关系的所有 y 值的集合。

{1 月 12 日、2 月 3 日、4 月 25 日、5 月 10 日、5 月 23 日、7 月 24 日、8 月 2 日、9 月 15 日}

示例\(\PageIndex{5}\)

使用显示的关系映射来

1. 列出关系的有序对
2. 找到关系的域
3. 找到关系的范围。

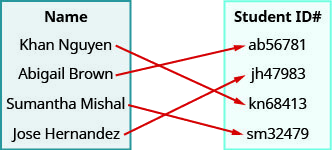
回答

ⓐ（Khanh Nguyen，kn68413），（阿比盖尔·布朗，ab56781），（Sumantha Mishal，sm32479），（Jose Hern and ez，jh47983）

ⓑ {Khanh Nguyen、Abigail Brown、Sumantha Mishal、Jose Hern 和 ez}

ⓒ {kn68413、ab56781、sm32479、jh47983}

示例\(\PageIndex{6}\)

使用显示的关系映射来

1. 列出关系的有序对
2. 找到关系的域
3. 找到关系的范围。

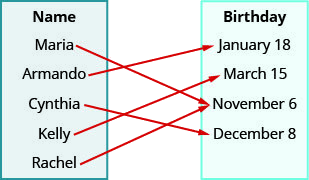
回答

ⓐ（玛丽亚，11 月 6 日），（Arm and o，1 月 18 日），（辛西娅，12 月 8 日），（凯利，3 月 15 日），（雷切尔，11 月 6 日）

ⓑ {Maria、Arm and o、Cynthia、Kelly、Rachel}

ⓒ {11 月 6 日、1 月 18 日、12 月 8 日、3 月 15 日}

图表是表示关系的另一种方式。 绘制的所有点的有序对集合是关系。 所有 x 坐标的集合是关系的域，所有 y 坐标的集合是范围。 通常，我们会按域和范围的升序写入数字。

示例\(\PageIndex{7}\)

使用关系图

1. 列出关系的有序对
2. 找到关系的域
3. 找到关系的范围。

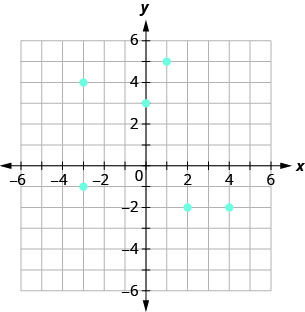
回答

ⓐ 关系的有序对是：\[{\{(1,5),(−3,−1),(4,−2),(0,3),(2,−2),(−3,4)}\}.\nonumber\]

ⓑ 域是关系的所有 x 值的集合：\(\quad {\{−3,0,1,2,4}\}\)。

请注意，在\(−3\)重复时，它只列出一次。

ⓒ 范围是关系的所有 y 值的集合：\(\quad {\{−2,−1,3,4,5}\}\)。

请注意，在\(−2\)重复时，它只列出一次。

示例\(\PageIndex{8}\)

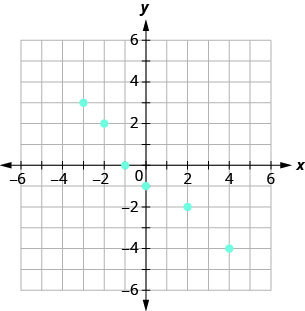
使用关系图

1. 列出关系的有序对
2. 找到关系的域
3. 找到关系的范围。
4. 

回答

ⓐ\((−3,3),(−2,2),(−1,0),\)
\((0,−1),(2,−2),(4,−4)\)
ⓑ\({\{−3,−2,−1,0,2,4}\}\)
ⓒ\({\{3,2,0,−1,−2,−4}\}\)

示例\(\PageIndex{9}\)

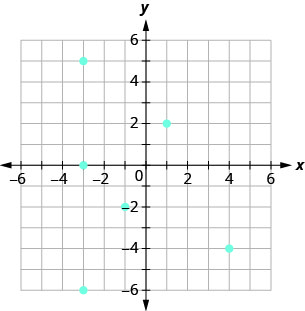
使用关系图

1. 列出关系的有序对
2. 找到关系的域
3. 找到关系的范围。

回答

ⓐ\((−3,0),(−3,5),(−3,−6),\)
\((−1,−2),(1,2),(4,−4)\)
ⓑ\({\{−3,−1,1,4}\}\)
ⓒ\({\{−6,0,5,−2,2,−4}\}\)

确定关系是否为函数

数学中广泛存在一种特殊的关系，称为函数。 函数是一种关系，它为其域中的每个元素分配区间中的一个元素。 对于关系中的每个有序对，每个 x 值仅与一个 y 值匹配。

定义：函数

函数是一种关系，它为其域中的每个元素分配区间中的一个元素。

Example 中的生日示例可以帮助我们理解这个定义。 每个人都有生日，但没有人有两个生日。 两个人共享生日是可以的。 ^{没关系 Danny 和 Stephen 将 7 月 24 日当作生日，那个 6 月，Liz 共享 8 月 2 日。} 由于每个人只有一个生日，因此示例中的关系是一种函数。

示例中图表显示的关系包括有序对\((−3,−1)\)和\((−3,4)\)。 在函数中可以吗？ 不，因为这就像一个人有两个不同的生日。

示例\(\PageIndex{10}\)

使用这组有序对来 (i) 确定关系是否为函数 (ii) 找到关系域 (iii) 找到关系的范围。

1. \({\{(−3,27),(−2,8),(−1,1),(0,0),(1,1),(2,8),(3,27)}\}\)
2. \({\{(9,−3),(4,−2),(1,−1),(0,0),(1,1),(4,2),(9,3)}\}\)

回答

ⓐ\({\{(−3,27),(−2,8),(−1,1),(0,0),(1,1),(2,8),(3,27)}\}\)

(i) 每个 x 值仅与一个 y 值匹配。 因此，这种关系是一种函数。

(ii) 域是关系中所有 x 值的集合。
域名是:\({\{−3,−2,−1,0,1,2,3}\}\).

(iii) 范围是关系中所有 y 值的集合。 请注意，我们不会两次列出范围值。
范围是:\({\{27,8,1,0}\}\).

ⓑ\({\{(9,−3),(4,−2),(1,−1),(0,0),(1,1),(4,2),(9,3)}\}\)

(i) x 值 9 与两个 y 值匹配，均为 3 和\(−3\)。 因此，这种关系不是函数。

(ii) 域是关系中所有 x 值的集合。 请注意，我们不会两次列出域值。
域名是:\({\{0,1,2,4,9}\}\).

(iii) 范围是关系中所有 y 值的集合。
范围是:\({\{−3,−2,−1,0,1,2,3}\}\).

示例\(\PageIndex{11}\)

使用这组有序对来 (i) 确定关系是否为函数 (ii) 找到关系域 (iii) 找出函数的范围。

1. \({\{(−3,−6),(−2,−4),(−1,−2),(0,0),(1,2),(2,4),(3,6)}\}\)
2. \({\{(8,−4),(4,−2),(2,−1),(0,0),(2,1),(4,2),(8,4)}\}\)

回答

ⓐ 是的;\({\{−3,−2,−1,0,1,2,3}\}\);
\({\{−6,−4,−2,0,2,4,6}\}\)
ⓑ 没有;\({\{0,2,4,8}\}\);
\({\{−4,−2,−1,0,1,2,4}\}\)

示例\(\PageIndex{12}\)

使用这组有序对来 (i) 确定关系是否为函数 (ii) 找到关系域 (iii) 找到关系的范围。

1. \({\{(27,−3),(8,−2),(1,−1),(0,0),(1,1),(8,2),(27,3)}\}\)
2. \({\{(7,−3),(−5,−4),(8,−0),(0,0),(−6,4),(−2,2),(−1,3)}\}\)

回答

ⓐ 不;\({\{0,1,8,27}\}\);
\({\{−3,−2,−1,0,2,2,3}\}\)
ⓑ 是的;\({\{7,−5,8,0,−6,−2,−1}\}\);
\({\{−3,−4,0,4,2,3}\}\)

示例\(\PageIndex{13}\)

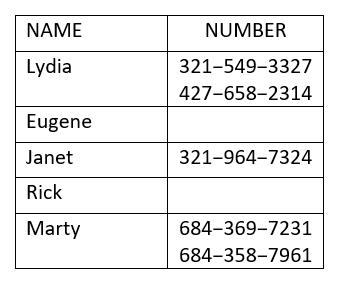
使用映射来

1. 确定关系是否为函数
2. 找到关系的域
3. 找到关系的范围。

回答

ⓐ 莉迪亚和马蒂都有两个电话号码。 因此，每个 x 值不只与一个 y 值匹配。 因此，这种关系不是函数。

ⓑ 该域是关系中所有 x 值的集合。 域名是：{莉迪亚、尤金、珍妮特、瑞克、马蒂}

ⓒ 范围是关系中所有 y 值的集合。 范围是：

\({\{321-549-3327, 427-658-2314, 321-964-7324, 684-358-7961, 684-369-7231, 798-367-8541}\}\)

示例\(\PageIndex{14}\)

使用映射来 ⓐ 确定关系是否为函数 ⓑ 找到关系的域 ⓒ 找到关系的范围。

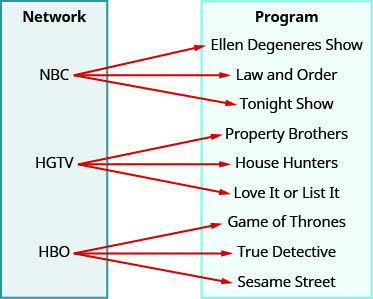
回答

ⓐ no ⓑ {NBC、HGTV、HBO} ⓒ {Ellen Degeneres Show、Law and Order、Tonight Show、Property Brothers、House Hunters、LOVE IT Or List it、True Street}

示例\(\PageIndex{15}\)

使用映射来

1. 确定关系是否为函数
2. 找到关系的域
3. 找到关系的范围。

 

回答

ⓐ 不 ⓑ {尼尔、克里斯塔尔、开尔文、乔治、克里斯塔、迈克} ⓒ {123-567-4839 工作、231-378-5941 cell、743-469-9731 cell、567-534-2971 cell、639-8471 cell}

在代数中，函数通常由方程表示。 求解 y 时，最容易看出方程是否为函数。 如果 x 的每个值只产生一个 y 值，则方程定义了一个函数。

示例\(\PageIndex{16}\)

确定每个方程是否为函数。

1. \(2x+y=7\)
2. \(y=x^2+1\)
3. \(x+y^2=3\)

回答

ⓐ\(2x+y=7\)

对于 x 的每个值，我们将其乘以，\(−2\)然后将 7 相加，得到 y 值

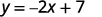
例如，如果\(x=3\)：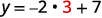

那我们什么时候\(x=3\)就知道\(y=1\)了。 对于 x 的任何值，它的工作原理类似。 由于 x 的每个值仅对应 y 的一个值，因此方程定义了一个函数。

ⓑ\(y=x^2+1\)

对于 x 的每个值，我们将其平方，然后加 1 得到 y 值。

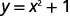
例如，如果\(x=2\)：

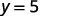
那我们什么时候\(x=2\)就知道\(y=5\)了。 对于 x 的任何值，它的工作原理类似。 由于 x 的每个值仅对应 y 的一个值，因此方程定义了一个函数。

ⓒ

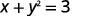
分离 y 项。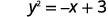
让我们替换\(x=2\)。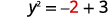
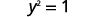
这为我们提供了 y 的两个值。	\(y=1\space y=−1\)

我们已经证明了何时\(x=2\)、那时\(y=1\)和\(y=−1\)。 对于 x 的任何值，它的工作原理类似。 由于 x 的每个值不只对应 y 的一个值，因此方程未定义函数。

示例\(\PageIndex{17}\)

确定每个方程是否为函数。

1. \(4x+y=−3\)
2. \(x+y^2=1\)
3. \(y−x^2=2\)

回答

ⓐ 是的 ⓑ 不 ⓒ 是的

示例\(\PageIndex{18}\)

确定每个方程是否为函数。

1. \(x+y^2=4\)
2. \(y=x^2−7\)
3. \(y=5x−4\)

回答

ⓐ 不 ⓑ 是的 ⓒ 是的

找出一个函数的值

命名一个函数非常方便，我们通常将其命名为 f、g、h、F、G 或 H。 在任何函数中，对于来自域的每个 x 值，我们都会得到区间中相应的 y 值。 对于该函数\(f\)，我们将此范围值写\(y\)为\(f(x)\)。 这称为函数表示法，被读取\(f\)\(x\)或读取\(f\) at 的值\(x\)。 在这种情况下，圆括号并不表示乘法。

定义：函数表示法

对于这个函数\(y=f(x)\)

\[\begin{array} {l} {f\text{ is the name of the function}} \\{x \text{ is the domain value}} \\ {f(x) \text{ is the range value } y \text{ corresponding to the value } x} \\ \nonumber \end{array}\]

我们从\(f(x)\) a\(f\) t\(x\) 或\(f\) at 的值读取\(x\)。

我们称 x 为自变量，因为它可以是域中的任何值。 我们称之为因变量 y，因为它的值取决于 x。

自变量和因变量

对于这个函数\(y=f(x)\)，

\[\begin{array} {l} {x \text{ is the independent variable as it can be any value in the domain}} \\ {y \text{ the dependent variable as its value depends on } x} \\ \nonumber \end{array}\]

就像你第一次遇到变量 x 时一样，函数表示法可能相当令人不安。 看起来很奇怪，因为它是新的。 当你使用这个符号时，你会觉得它更舒服。

让我们来看看这个方程式\(y=4x−5\)。 为了找出 y 的值\(x=2\)，我们知道用替换\(x=2\)成方程然后进行简化。

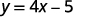让 x=2。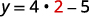

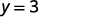处的函数值\(x=2\)为 3。

我们使用函数表示法做同样的事情，方程\(y=4x−5\)可以写成\(f(x)=4x−5\)。 为了找出何时的值\(x=2\)，我们这样写：

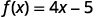让 x=2。

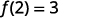处的函数值\(x=2\)为 3。

为给定值 x\(f(x)\) 求值的过程称为对函数求值。

示例\(\PageIndex{19}\)

对于函数\(f(x)=2x^2+3x−1\)，计算该函数。

1. \(f(3)\)
2. \(f(−2)\)
3. \(f(a)\)

回答

ⓐ

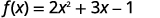
要进行计算\(f(3)\)，请用 3 代替 x。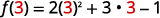
简化。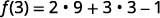

ⓑ

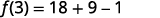
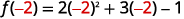
简化。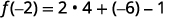

ⓒ

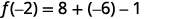
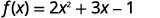
要计算 f (a)、f (a)，用 a 代替 x。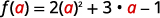
简化。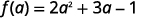

示例\(\PageIndex{20}\)

对于函数\(f(x)=3x^2−2x+1\)，计算该函数。

1. \(f(3)\)
2. \(f(−1)\)
3. \(f(t)\)

回答

ⓐ\(f(3)=22\) ⓑ\(f(−1)=6\) ⓒ\(f(t)=3t^2−2t−1\)

示例\(\PageIndex{21}\)

对于函数\(f(x)=2x^2+4x−3\)，计算该函数。

1. \(f(2)\)
2. \(f(−3)\)
3. \(f(h)\)

回答

ⓐ\((2)=13\) ⓑ\(f(−3)=3\)
ⓒ\(f(h)=2h2+4h−3\)

在最后一个例子中，我们找到\(f(x)\)了一个常量值 x。 在下一个示例中，我们被要求查找值\(g(x)\)为 x 的变量。 我们仍然遵循相同的程序，用中的变量代替 x。

示例\(\PageIndex{22}\)

对于函数\(g(x)=3x−5\)，计算该函数。

1. \(g(h^2)\)
2. \(g(x+2)\)
3. \(g(x)+g(2)\)

回答

ⓐ

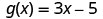
要进行计算\(g(h^2)\)，请\(h^2\)替换 x。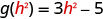

ⓑ

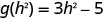
要进行计算\(g(x+2)\)，请\(x+2\)替换 x。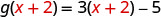
简化。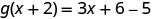

ⓒ

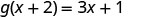
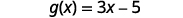
要进行评估\(g(x)+g(2)\)，请先找到\(g(2)\)。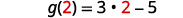
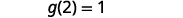
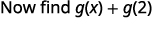
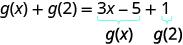
简化。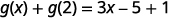

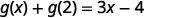
注意 ⓑ 和 ⓒ 部分之间的区别。 我们明白\(g(x+2)=3x+1\)了\(g(x)+g(2)=3x−4\)。 所以我们明白了\(g(x+2)\neq g(x)+g(2)\)。

示例\(\PageIndex{23}\)

对于函数\(g(x)=4x−7\)，计算该函数。

1. \(g(m^2)\)
2. \(g(x−3)\)
3. \(g(x)−g(3)\)

回答

ⓐ\(4m^2−7\) ⓑ\(4x−19\)
ⓒ\(x−12\)

示例\(\PageIndex{24}\)

对于函数\(h(x)=2x+1\)，计算该函数。

1. \(h(k^2)\)
2. \(h(x+1)\)
3. \(h(x)+h(1)\)

回答

ⓐ\(2k^2+1\) ⓑ\(2x+3\)
ⓒ\(2x+4\)

许多日常情况都可以使用函数进行建模。

示例\(\PageIndex{25}\)

西尔维亚账户中未读的电子邮件数量为75封。 这个数字每天增加10封未读电子邮件。 该函数\(N(t)=75+10t\)表示电子邮件数量 N 和时间 t（以天为单位）之间的关系。

1. 确定自变量和因变量。
2. 查找\(N(5)\)。 解释这个结果是什么意思。

回答

ⓐ 未读电子邮件的数量是天数的函数。 未读电子邮件的数量 N 取决于天数 t。 因此，变量 N 是因变量，变量 tt 是自变量。

ⓑ 查找\(N(5)\)。 解释这个结果是什么意思。

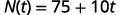
在 t=5.t=5 中替换。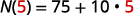
简化。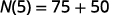

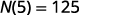
由于 5 是天数\(N(5)\)，是 5 天后未读电子邮件的数量。 5 天后，账户中有 125 封未读电子邮件。

示例\(\PageIndex{26}\)

Bryan 账户中未读电子邮件的数量为 100。 这个数字每天增加15封未读电子邮件。 该函数\(N(t)=100+15t\)表示电子邮件数量 N 和时间 t（以天为单位）之间的关系。

1. 确定自变量和因变量。
2. 查找\(N(7)]\)。 解释这个结果是什么意思。

回答

ⓐ t IND; N DEP ⓑ 205；Bryan 账户中第七天未读电子邮件的数量。

示例\(\PageIndex{27}\)

安东尼账户中未读的电子邮件数量为110封。 这个数字每天增加25封未读电子邮件。 该函数\(N(t)=110+25t\)表示电子邮件数量 N 和时间 t（以天为单位）之间的关系。

1. 确定自变量和因变量。
2. 查找\(N(14)\)。 解释这个结果是什么意思。

回答

ⓐ t IND; N DEP ⓑ 460；第十四天安东尼账户中未读的电子邮件数量

访问此在线资源，获取有关关系和功能的更多指导和练习。

• 函数简介

关键概念

• 函数表示法：用于函数\(y=f(x)\)
  • f 是函数的名称
  • x 是域值
  • \(f(x)\)是区间值 y，对应于
    我们读取\(f(x)\)为 x 的 f 或 x 处的 f 的值。
• 自变量和因变量：对于函数\(y=f(x)\)，
  • x 是自变量，因为它可以是域中的任何值
  • y 是因变量，因为它的值取决于 x

词汇表

关系域

关系的域是关系的有序对中的所有 x 值。

函数

函数是一种关系，它为其域中的每个元素分配区间中的一个元素。

制图

映射有时用于显示关系。 箭头显示域元素与范围元素的配对。

关系范围

关系的范围是关系的有序对中的所有 y 值。

关系

关系是任意一组有序对 (x, y)。 (x, y)。 有序对中的所有 x 值共同构成了域。 有序对中的所有 y 值共同构成了范围。