3.5E：练习

练习成就完美

验证两个变量中不等式的解

在以下练习中，确定每个有序对是否是给定不等式的解。

1。 确定每个有序对是否是不等式的解\(y>x−1\)：

a.\((0,1)\)
b.\((−4,−1)\)
c.\((4,2)\)
d.\((3,0)\)
e.\((−2,−3)\)

回答

a. 是的 b. 是的 c. 不 d. 不 e. 不

2。 确定每个有序对是否是不等式的解\(y>x−3\)：

a.\((0,0)\)
b.\((2,1)\)
c.\((−1,−5)\)
d.\((−6,−3)\)
e.\((1,0)\)

3。 确定每个有序对是否是不等式的解\(y<3x+2\)：

a.\((0,3)\)
b.\((−3,−2)\)
c.\((−2,0)\)
d.\((0,0)\)
e.\((−1,4)\)

回答

a. 不 b. 不 c. 是的 d. 是的 e. 不

4。 确定每个有序对是否是不等式的解\(y<−2x+5\)：

a.\ (−3,0) (−3,0)
b.\((1,6)\)
c.\((−6,−2)\)
d.\((0,1)\)
e.\((5,−4)\)

5。 确定每个有序对是否是不等式的解\(3x−4y>4\)：

a.\((5,1)\)
b.\((−2,6)\)
c.\((3,2)\)
d.\((10,−5)\)
e.\((0,0)\)

回答

a. 是的 b. 不 c. 不 d. 不 e. 不

6。 确定每个有序对是否是不等式的解\(2x+3y>2\)：

a.\((1,1)\)
b.\((4,−3)\)
c.\((0,0)\)
d.\((−8,12)\)
e.\((3,0)\)

认识不等式解与其图之间的关系

在以下练习中，写下阴影区域所示的不等式。

7。 用边界线写下图表所示的不等式\(y=3x−4\)。

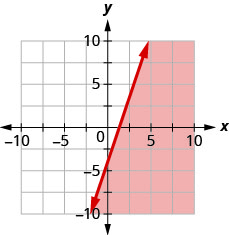
回答

\(y\leq 3x−4\)

8。 用边界线写下图表所示的不等式\(y=2x−4\)。

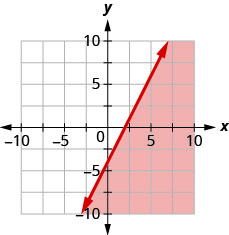
9。 用边界线写下图表所示的不等式\(y=−\frac{1}{2}x+1\)。

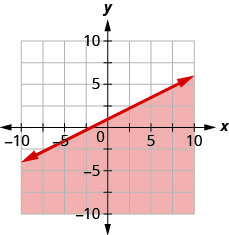
回答

\(y\leq −\frac{1}{2}x+1\)

10。 用边界线写下图表所示的不等式\(y=-\frac{1}{3}x−2\)。

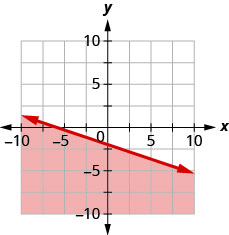
11。 用边界线写下图中阴影区域所示的不等式\(x+y=5\)。

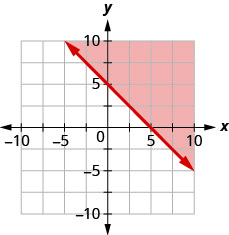
回答

\(x+y\geq 5\)

12。 用边界线写下图中阴影区域所示的不等式\(x+y=3\)。

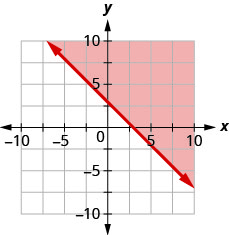
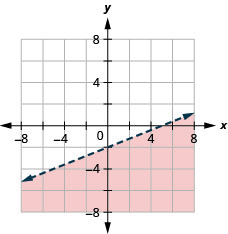
13。 用边界线写下图中阴影区域所示的不等式\(3x−y=6\)。

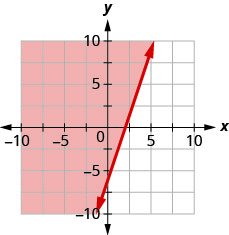
回答

\(3x−y\leq 6\)

14。 用边界线写下图中阴影区域所示的不等式\(2x−y=4\)。

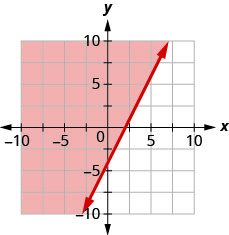
绘制两个变量中的线性不等式

在以下练习中，绘制每个线性不等式的图表。

15。 绘制线性不等式图:\(y>\frac{2}{3}x−1\).

回答

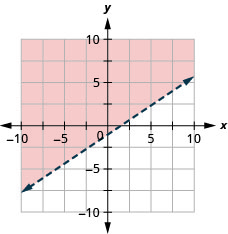
16。 绘制线性不等式图:\(y<\frac{3}{5}x+2\).

17。 绘制线性不等式图:\(y\leq −\frac{1}{2}x+4\).

回答

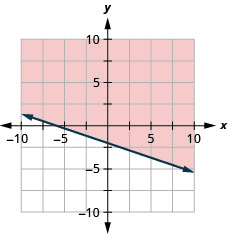
18。 绘制线性不等式图:\(y\geq −\frac{1}{3}x−2\).

19。 绘制线性不等式图:\(x−y\leq 3\).

回答

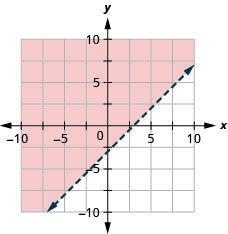
20。 绘制线性不等式图:\(x−y\geq −2\).

21。 绘制线性不等式图:\(4x+y>−4\).

回答

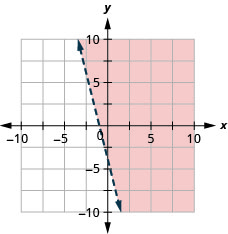
22。 绘制线性不等式图:\(x+5y<−5\).

23。 绘制线性不等式图:\(3x+2y\geq −6\).

回答

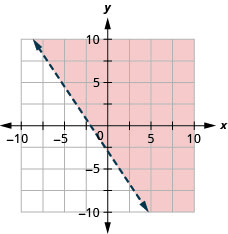
24。 绘制线性不等式图:\(4x+2y\geq −8\).

25。 绘制线性不等式图:\(y>4x\).

回答

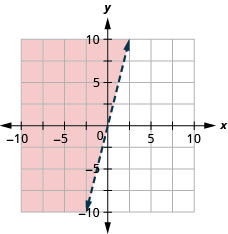
26。 绘制线性不等式图:\(y\leq −3x\).

27。 绘制线性不等式图:\(y<−10\).

回答

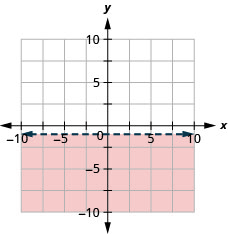
28。 绘制线性不等式图:\(y\geq 2\).

29。 绘制线性不等式图:\(x\leq 5\).

回答

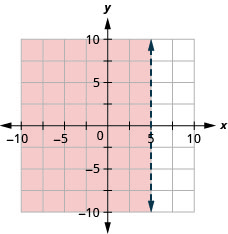
30。 绘制线性不等式图:\(x\geq 0\).

31。 绘制线性不等式图:\(x−y<4\).

回答

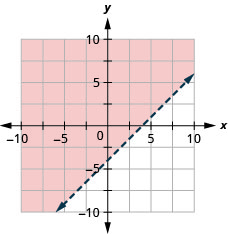
32。 绘制线性不等式图:\(x−y<−3\).

33。 绘制线性不等式图:\(y\geq \frac{3}{2}x\).

回答

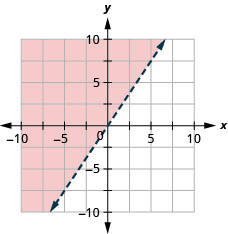
34。 绘制线性不等式图:\(y\leq \frac{5}{4}x\).

35。 绘制线性不等式图:\(y>−2x+1\).

回答

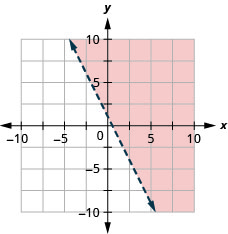
36。 绘制线性不等式图:\(y<−3x−4\).

37。 绘制线性不等式图:\(2x+y\geq −4\).

回答

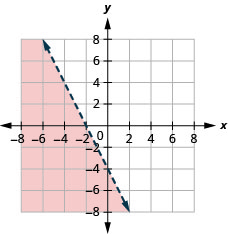
38。 绘制线性不等式图:\(x+2y\leq −2\).

39。 绘制线性不等式图:\(2x−5y>10\).

回答

40。 绘制线性不等式图:\(4x−3y>12\).

使用两个变量中的线性不等式求解应用程序

41。 哈里森有两份兼职工作。 一个在加油站，每小时支付11美元，另一个是IT故障排除，每小时16.50美元16.50美元。 在这两份工作之间，哈里森希望每周至少赚330美元。 哈里森每份工作需要工作多少小时才能赚到至少 330 美元？

a. 假设 x 是他在加油站工作的小时数，让 y 是他进行故障排除的（小时）。 写一个不等式来模拟这种情况。

b. 绘制不等式图。

c. 找到三个可以解决\((x,y)\)不等式的有序对。 然后，解释这对哈里森意味着什么。

回答

a.\(11x+16.5y\geq 330\)
b。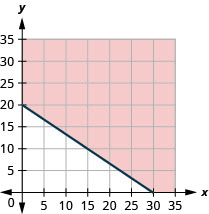

c. 答案视情况而定。

42。 艾琳娜在暑假期间每周至少需要赚450美元才能支付大学费用。 她有两份工作。 一个是游泳教练，每小时支付9美元，另一个是遗传学实验室的实习生，每小时22.50美元。 Elena每份工作需要工作多少小时才能每周至少赚450美元？

a. 让 x 成为她教游泳的小时数，让 y 成为她作为实习生工作的小时数。 写一个不等式来模拟这种情况。

b. 绘制不等式图。

c. 找到三个可以解决不等式的有序对 (x, y) (x, y)。 然后，解释一下这对埃琳娜意味着什么。

43。 医生告诉劳拉，她需要足够的运动才能每天消耗 500 卡路里的热量。 她喜欢跑步或骑自行车，跑步时每分钟消耗 15 卡路里，骑自行车时每分钟消耗 10 卡路里。

a. 如果 x 是 Laura 跑步的分钟数，y 是她骑自行车的分钟数，则找出模拟情况的不等式。

b. 绘制不等式图。

c. 列出解决不平等的三种方法。 解决方案为劳拉提供了哪些选择？

回答

a.\(15x+10y\geq 500\)
b。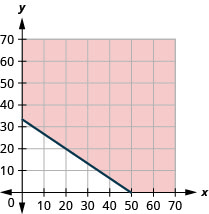

c. 答案视情况而定。

44。 阿曼多的锻炼包括跆拳道和游泳。 跆拳道时，他每分钟消耗 10 卡路里的热量，游泳时每分钟消耗 7 卡路里的热量。 他想每天消耗 600 卡路里的热量。

a. 如果 x 是 Armando 踢球的分钟数，y 是他将要游泳的分钟数，那就找出有助于阿曼多为今天创造锻炼的不平等性。

b. 绘制不等式图。

c. 列出解决不平等的三种方法。 这些解决方案为阿曼多提供了哪些选择？

写作练习

45。 莱斯特认为，任何带有 >> 符号的不等式的解是线上方的区域，任何带有 << 符号的不等式的解是线下区域。 莱斯特是对的吗？ 解释原因或原因。

回答

答案会有所不同。

46。 解释为什么，在某些线性不等式图中，边界线是实线，而在其他图中，边界线是虚线。

自检

a. 完成练习后，使用此清单评估您对本节目标的掌握程度。

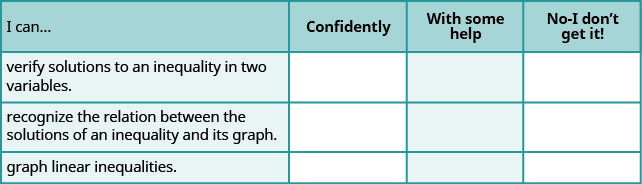
b. 在 1-10 的评分中，根据你在清单上的回答，你会如何评价你对本部分的掌握程度？ 你怎么能改善这个？