3.5:绘制两个变量中的线性不等式
- Page ID
- 203858
在本节结束时,您将能够:
- 验证两个变量中不等式的解。
- 认识不等式解与其图之间的关系。
- 绘制两个变量中的线性不等式
- 使用两个变量中的线性不等式求解应用程序
在开始之前,请参加这个准备测验。
验证两个变量中不等式的解
以前我们学会了只用一个变量求解不等式。 现在,我们将学习包含两个变量的不等式。 特别是,我们将研究两个变量中的线性不等式,它们与两个变量中的线性方程非常相似。
两个变量中的线性不等式有许多用途。 例如,如果你经营一家企业,你会希望你的收入大于成本,这样你的企业才能获利。
线性不等式是一种可以用以下形式之一书写的不等式:
\( \begin{array} {l} { }& {Ax+By>C} &{Ax+By\geq C} &{Ax+By<C} &{Ax+By\leq C} \\ \end{array} \)
其中 A 和 B 不都为零。
回想一下,具有一个变量的不等式有许多解。 例如,不等式 x>3x>3 的解是任何大于 3 的数字。 我们在数字行上显示了这一点,方法是在 3 右边的数字行中加上阴影,然后在 3 处加一个左括号。 见图。

同样,两个变量中的线性不等式有许多解。 当我们在值中替换时,任何使不等式成真的有序对 (x, y) (x, y) 都是线性不等式的解。
当我们替换 x 和 y 的值时,如果不等式为真,则有序对\((x,y)\)是线性不等式的解。
确定每个有序对是否是不等式的解 y>x+4: y>x+4:
ⓐ (0,0) (0,0) ⓑ (1,6) (1,6) ⓒ (2,6) (2,6) ⓓ (−5, −15) (−5, −15) ⓔ (−8,12) (−8,12)
- 回答
-
ⓐ
\((0,0)\) 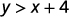
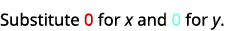
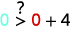
简化。 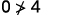
所以,\((0,0)\)不是解决办法\(y>x+4\)。
ⓑ
\((1,6)\) 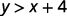
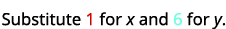
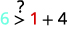
简化。 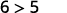
所以,\((1,6)\)是一个解决方案\(y>x+4\)。 ⓒ
\((2,6)\) 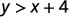
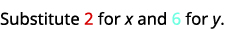
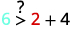
简化。 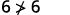
所以,\((2,6)\)不是解决办法\(y>x+4\)。 ⓓ
\((−5,−15)\) 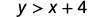
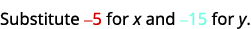
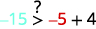
简化。 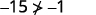
所以,\((−5,−15)\)不是解决办法\(y>x+4\)。 ⓔ
\((−8,12)\) 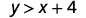
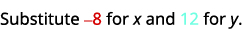
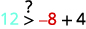
简化。 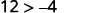
所以,\((−8,12)\)是一个解决方案\(y>x+4\)。
确定每个有序对是否是不等式的解\(y>x−3\):
ⓐ\((0,0)\) ⓑ\((4,9)\) ⓒ\((−2,1)\) ⓓ\((−5,−3)\) ⓔ\((5,1)\)
- 回答
-
ⓐ 是的 ⓑ 是的 ⓒ 是的 ⓓ 是的 ⓔ 不是
确定每个有序对是否是不等式的解\(y<x+1\):
ⓐ\((0,0)\) ⓑ\((8,6)\) ⓒ\((−2,−1)\) ⓓ\((3,4)\) ⓔ\((−1,−4)\)
- 回答
-
ⓐ 是的 ⓑ 是的 ⓒ 不 ⓓ 不 ⓔ 是的
认识不等式解与其图之间的关系
现在,我们将研究不等式的解与其图表有何关系。
让我们再想一想前面显示的数字线。 该点将该数字线\(x=3\)分为两部分。 3 的一面是所有小于 3 的数字。 在 3 的另一边,所有数字都大于 3。 参见图。
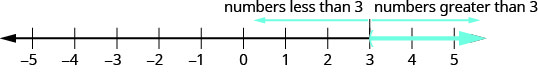
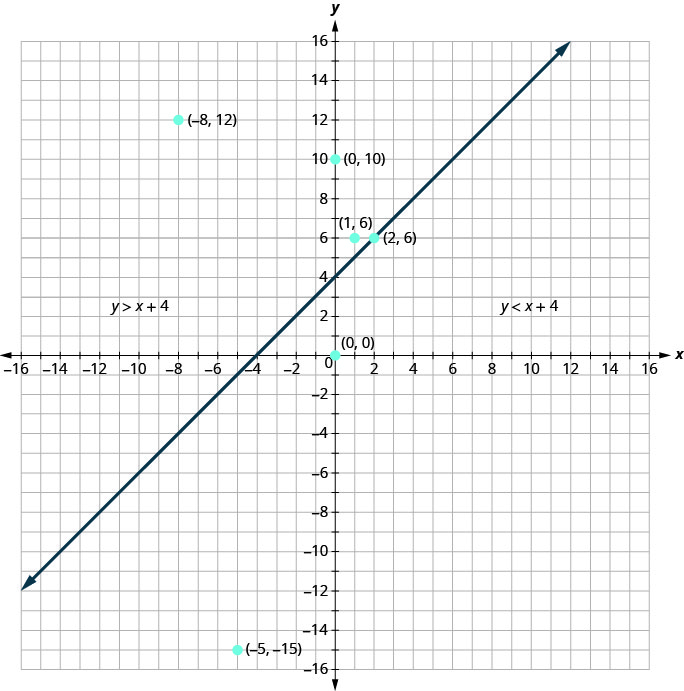
同样,这条线将平面\(y=x+4\)分成两个区域。 直线的一侧是带有以下点的点\(y<x+4\)。 在这条线的另一边是带有的点\(y>x+4\)。 我们称这条线\(y=x+4\)为边界线。
带方程的直线\(Ax+By=C\)是分隔区域与所在\(Ax+By>C\)区域的边界线\(Ax+By<C\)。
对于一个变量中的不等式,端点用圆括号或方括号显示,具体取决于解中是否包含 a:

同样,对于两个变量中的不等式,边界线以实线或虚线显示,以显示解中是否包含该直线。
\[ \begin{array} {ll} {Ax+By<C} &{Ax+By\leq C} \\ {Ax+By>C} &{Ax+By\geq C} \\ {\text{Boundary line is }Ax+By=C.} &{\text{Boundary line is }Ax+By=C.} \\ {\text{Boundary line is not included in solution.}} &{\text{Boundary line is not included in solution.}} \\ {\textbf{Boundary line is dashed.}} &{\textbf{Boundary line is solid.}} \\ \nonumber \end{array} \]
现在,让我们来看看我们在示例中发现了什么。 我们首先绘制直线\(y=x+4\),然后绘制我们测试的五个点,如图所示。 参见图。
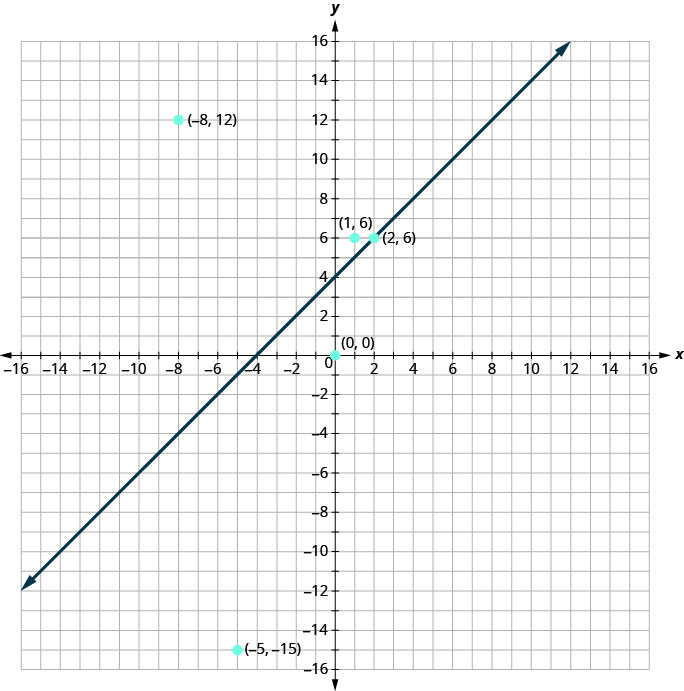
在示例中,我们发现有些要点是解决不平等的办法\(y>x+4\),有些则不是。
我们绘制的哪个点是解决不平等的办法\(y>x+4\)?
要点\((1,6)\)和\((−8,12)\)是解决不平等的办法\(y>x+4\)。 请注意,它们都位于边界线的同一侧\(y=x+4\)。
这两个点\((0,0)\)和\((−5,−15)\)位于边界线的另一边\(y=x+4\),它们不是不等式的解\(y>x+4\)。 对于这两点,\(y<x+4\).
那重点\((2,6)\)呢? 因为\(6=2+4\),该点是方程的解\(y=x+4\),但不是不等式的解\(y>x+4\)。 所以\((2,6)\)这个点在边界线上。
让我们在边界线上方再取一个点,测试它是否是不等式的解\(y>x+4\)。 这个点\((0,10)\)显然是指向边界线的上方,不是吗? 这是不平等的解决方案吗?
\[\begin{array} {lll} {y} &{>} &{x+4} \\ {10} &{\overset{?}{>}} &{0+4} \\ {10} &{>} &{4} \\ \nonumber \end{array}\]
所以,\((0,10)\)是一个解决方案\(y>x+4\)。
您在边界线上方选择的任何点都是不等式的解\(y>x+4\)。 边界线上方的所有点均为解。
同样,边界线以下的所有点,即带有\((0,0)\)和的边\((−5,−15)\),都不是解\(y>x+4\),如图所示。
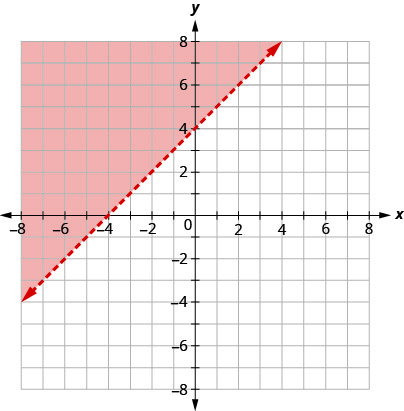
不等式的图\(y>x+4\)如下所示。
这条线\(y=x+4\)将飞机分为两个区域。 阴影部分显示了不等式的解决方案\(y>x+4\)。
边界线上的点和位置\(y=x+4\)上的点不是不等式的解\(y>x+4\),因此线本身不是解的一部分。 我们通过将直线设为虚线,而不是实线来证明这一点。
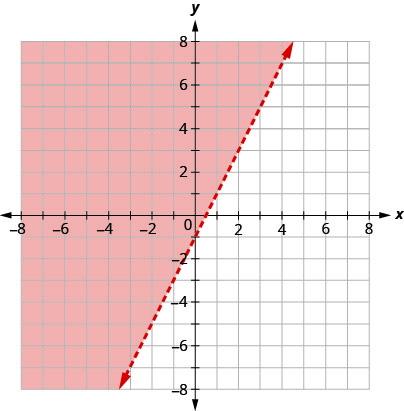
此图中显示的边界线是\(y=2x−1\)。 写下图表所示的不等式。
- 回答
-
这条线\(y=2x−1\)是边界线。 直线的一侧是带有\(y>2x−1\)的点,另一侧是带点的点\(y<2x−1\)。
让我们测试一下这个点\((0,0)\),看看哪个不等式描述了它相对于边界线的位置。
在\((0,0)\),哪个不平等是正确的:还\(y>2x−1\)是\(y<2x−1\)?
\[\begin{array} {ll} {y>2x−1} &{y<2x−1} \\ {0\overset{?}{>}2·0−1} &{0\overset{?}{<}2·0−1} \\ {0>−1\text{ True}} &{0<−1\text{ False}} \\ \nonumber \end{array}\]
因为,\(y>2x−1\)是真的\((0,0)\),那就是解决方案。 阴影区域显示了不等式的解决方案\(y>2x−1\)。
由于边界线是用实线绘制的,因此不等式包括等号。
该图显示了不等式\(y\geq 2x−1\)。
我们可以使用任何点作为测试点,前提是它不在线上。 我们为什么选择\((0,0)\)? 因为它是最容易评估的。 你可能需要在边界线的另一边选取一个点然后检查一下\(y<2x−1\)。
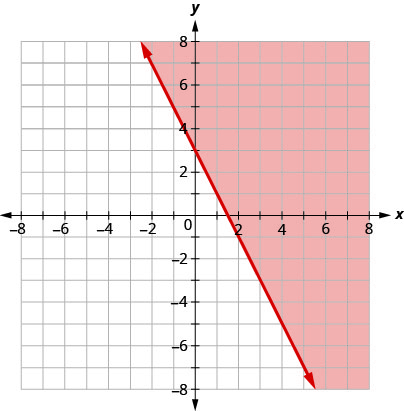
用边界线写下图表所示的不等式\(y=−2x+3\)。
- 回答
-
\(y\geq −2x+3\)
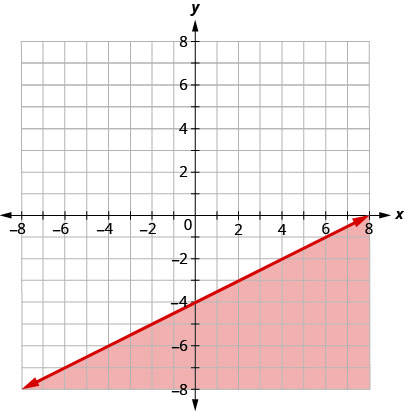
用边界线写下图表所示的不等式\(y=\frac{1}{2}x−4\)。
- 回答
-
\(y\leq \frac{1}{2}x−4\)
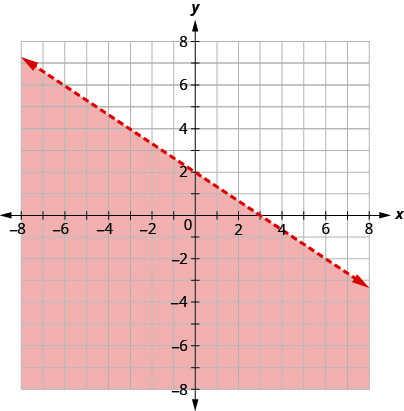
此图中显示的边界线是\(2x+3y=6\)。 写下图表所示的不等式。
- 回答
-
这条线\(2x+3y=6\)是边界线。 直线的一侧是带有\(2x+3y>6\)的点,另一侧是带点的点\(2x+3y<6\)。
让我们测试一下这个点\((0,0)\),看看哪个不等式描述了它的边界线边。
在\((0,0)\),哪个不平等是正确的:还\(2x+3y>6\)是\(2x+3y<6\)?
\[\begin{array} {ll} {2x+3y>6} &{2x+3y<6} \\ {2(0)+3(0)\overset{?}{>}6} &{2(0)+3(0)\overset{?}{<}6} \\ {0>6\text{ False}} &{0<6\text{ True}} \\ \nonumber \end{array}\]
所以,一边\((0,0)\)是哪一边\(2x+3y<6\)。
(你可能想在边界线的另一边选一个点然后检查一下\(2x+3y>6\)。)
由于边界线以虚线绘制,因此不等式不包含等号。
阴影区域显示了不平等的解决方案\(2x+3y<6\)。
用边界线写下图中阴影区域所示的不等式\(x−4y=8\)。
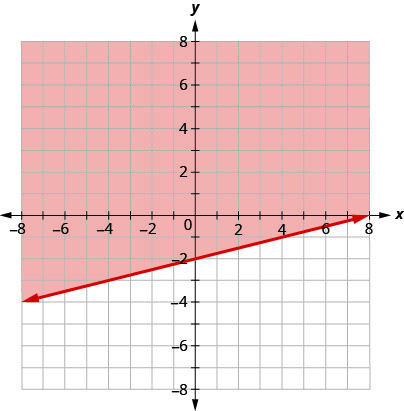
- 回答
-
\(x−4y\leq 8\)
用边界线写下图中阴影区域所示的不等式\(3x−y=6\)。
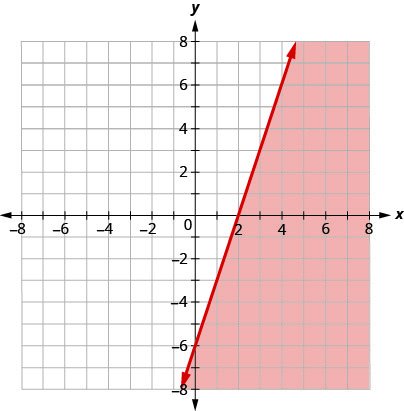
- 回答
-
\(3x−y\geq 6\)
绘制两个变量中的线性不等式
现在我们知道了线性不等式的图是什么样子以及它与边界方程的关系,我们可以利用这些知识来绘制给定的线性不等式。
绘制线性不等式图\(y\geq \frac{3}{4}x−2\)。
- 回答
-
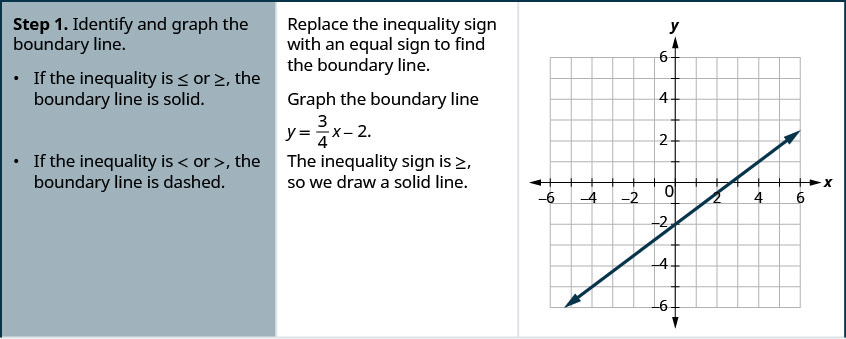

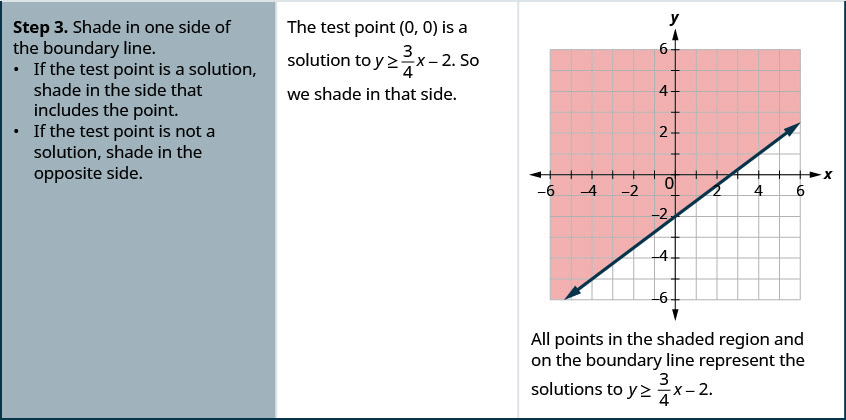
绘制线性不等式图\(y>\frac{5}{2}x−4\)。
- 回答
-
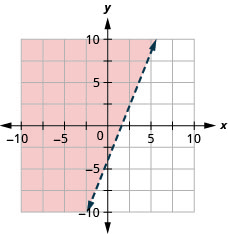
阴影区域和边界线上的所有点都表示解\(y>\frac{5}{2}x−4\)。
绘制线性不等式图\(y<\frac{2}{3}x−5\)。
- 回答
-
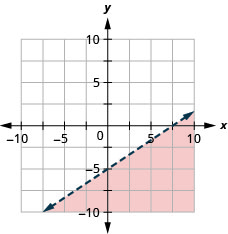
阴影区域中的所有点,但不是边界线上的点,都代表了解\(y<\frac{2}{3}x−5\)。
这里总结了我们绘制线性不等式图所采取的步骤。
- 识别边界线并绘制图表。
- 如果不等式为\ leq 或\ geq、\ leq 或\ geq,则边界线为实线。
- 如果不等式为 <or><or>,则边界线为虚线。
- 测试不在边界线上的点。 这是不平等的解决方案吗?
- 边界线一侧的阴影。
- 如果测试点是解,则在包含该点的一侧加上阴影。
- 如果测试点不是解决方案,则在另一侧遮阳。
绘制线性不等式图\(x−2y<5\)。
- 回答
-
首先,我们绘制边界线图\(x−2y=5\)。 不平等\(<\)之处在于我们画一条虚线。
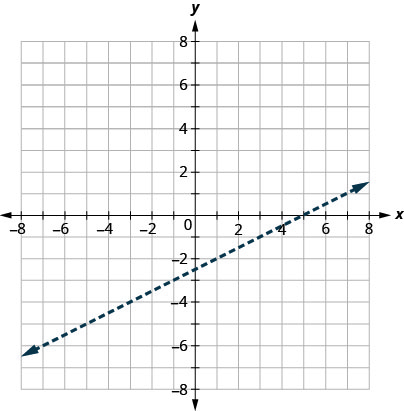
然后,我们测试一个点。 我们将\((0,0)\)再次使用,因为它易于评估并且不在边界线上。
\((0,0)\)有解决方案\(x−2y<5\)吗?
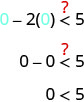
这个点\((0,0)\)是解\(x−2y<5\),所以我们在边界线的那一侧做阴影。
阴影区域中的所有点,但不是边界线上的点,都代表了解\(x−2y<5\)。
绘制线性不等式图:\(2x−3y<6\).
- 回答
-
阴影区域中的所有点,但不是边界线上的点,都代表了解\(2x−3y<6\)。
绘制线性不等式图:\(2x−y>3\).
- 回答
-
阴影区域中的所有点,但不是边界线上的点,都代表了解\(2x−y>3\)。
如果边界线穿过原点怎么办? 那么,我们将无法\((0,0)\)用作测试点。 没问题——我们只选择不在边界线上的其他点即可。
绘制线性不等式图:\(y\leq −4x\).
- 回答
-
首先,我们绘制边界线图\(y=−4x\)。 它采用斜率截距形式,带有 an\(m=−4\) d\(b=0\)。 不平等\(\leq\)之处在于我们画一条实线。

现在我们需要一个测试点。 我们可以看到点 (1,0) (1,0) 不在边界线上。
\((1,0)\)有解决方案\(y\leq −4x\)吗?
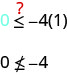
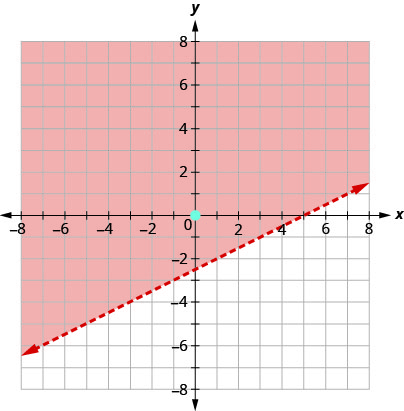
这个点\((1,0)\)不是解法\(y\leq −4x\),所以我们在边界线的另一侧进行阴影。
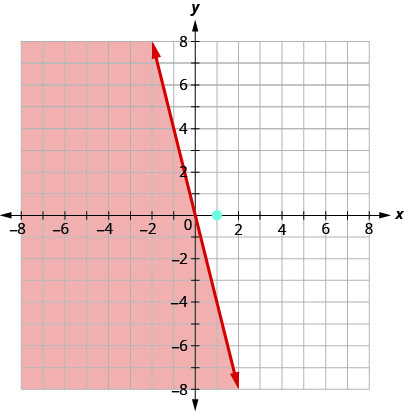
阴影区域和边界线上的所有点都表示解\(y\leq −4x\)。
绘制线性不等式图:\(y>−3x\).
- 回答
-
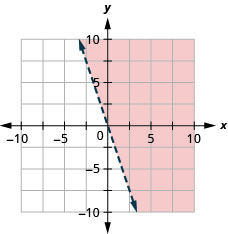
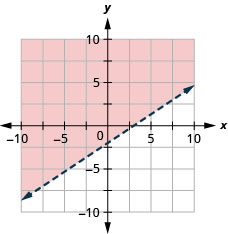
阴影区域中的所有点,但不是边界线上的点,都代表了解\(y>−3x\)。
绘制线性不等式图:\(y\geq −2x\).
- 回答
-
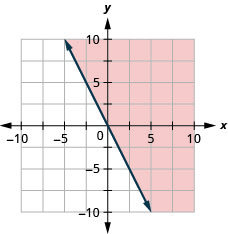
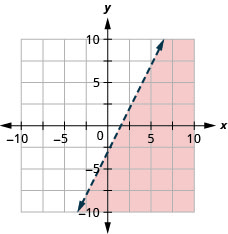
阴影区域和边界线上的所有点都表示解\(y\geq −2x\)。
一些线性不等式只有一个变量。 它们可能有 x 但没有 y,或者是 y 但没有 x。 在这些情况下,边界线要么是垂直线,要么是水平线。
回想一下:
\[\begin{array} {ll} {x=a} &{\text{vertical line}} \\ {y=b} &{\text{horizontal line}} \\ \nonumber \end{array}\]
绘制线性不等式图:\(y>3\).
- 回答
-
首先,我们绘制边界线图\(y=3\)。 它是一条水平线。 不平等\(>\)之处在于我们画一条虚线。
我们测试一下\((0,0)\)。
\[y>3\nonumber\]\[0\slashed{>}3\nonumber\]
所以,\((0,0)\)不是解决办法\(y>3\)。
因此,我们对不包括的侧面进行遮蔽\((0,0)\),如图所示。
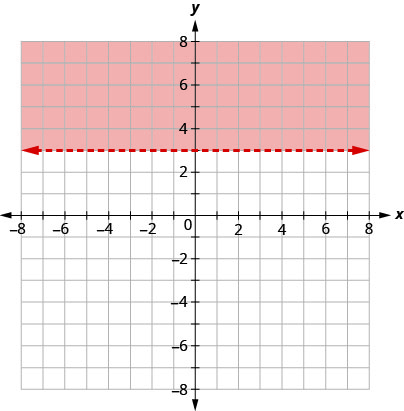
阴影区域中的所有点,但不是边界线上的点,都代表了解\(y>3\)。
绘制线性不等式图:\(y<5\).
- 回答
-
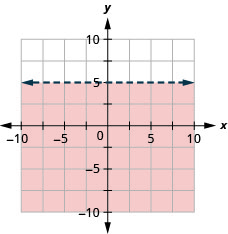
阴影区域中的所有点,但不是边界线上的点,都代表了解\(y<5\)。
绘制线性不等式图:\(y\leq −1\).
- 回答
-
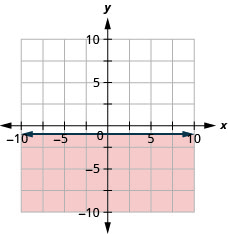
阴影区域和边界线上的所有点都表示解\(y\leq −1\)。
使用两个变量中的线性不等式求解应用程序
许多字段使用线性不等式对问题进行建模。 虽然我们的例子可能涉及简单的情况,但它们为我们提供了培养技能并感受如何使用技能的机会。
希拉里亚从事两份兼职工作,以便赚到足够的钱来履行每周至少240美元的义务。 她的餐饮服务工作每小时支付10美元,而她在校园的辅导工作每小时支付15美元。 Hilaria 每份工作需要工作多少小时才能赚到至少 240 美元?
ⓐ 让 xx 成为她在餐饮服务部门工作的小时数,让 y 成为她工作辅导的小时数。 写一个不等式来模拟这种情况。
ⓑ 绘制不等式图。
ⓒ 找到三个可以解决\((x,y)\)不等式的有序对。 然后,解释这对希拉里亚意味着什么。
- 回答
-
ⓐ 我们让 x 成为她在餐饮服务部门工作的小时数,让 y 成为她工作辅导的小时数。
她在餐饮服务工作中每小时的收入为10美元,辅导每小时为15美元。 在每项工作中,工时数乘以小时工资将得出该工作所赚取的金额。
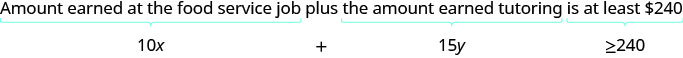
ⓑ 为了绘制不等式图,我们将其绘制为斜率截距形式。
\[\begin{align} {10x+15y} &\geq 240 \\ 15y &\geq -10x+240 \\ y &\geq {−\frac{2}{3}x+16} \\ \nonumber \end{align}\]
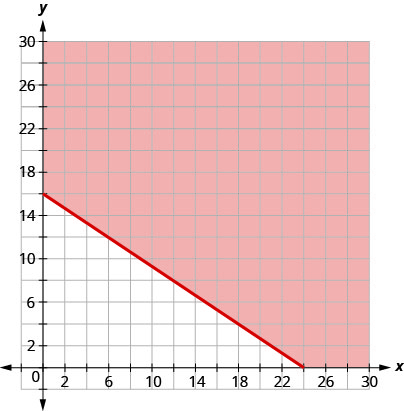
ⓒ 从图中我们可以看出,有序对\((15,10)\)\((24,0)\)代表无限多解中的三个。\((0,16)\) 检查不等式中的值。
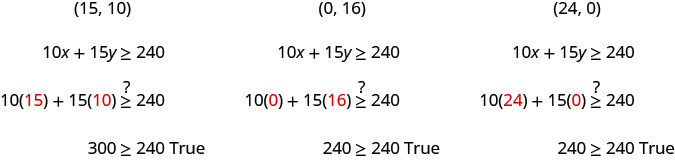
对于Hilaria来说,这意味着要赚到至少240美元,她可以工作15个小时的辅导和10个小时的快餐工作,16个小时的辅导赚取所有钱,或者在餐饮服务工作24小时时赚到所有的钱。
Hugh 有两份兼职工作。 一个在杂货店,每小时支付10美元,另一个是保姆,每小时13美元。 在这两份工作之间,休希望每周至少赚260美元。 Hugh 每份工作需要工作多少小时才能赚到至少 260 美元?
ⓐ 假设 x 是他在杂货店工作的小时数,让 y 成为他保姆的小时数。 写一个不等式来模拟这种情况。
ⓑ 绘制不等式图。
ⓒ 找到三个可以解决不等式的有序对(x,y)。 然后,解释一下这对休意味着什么。
- 回答
-
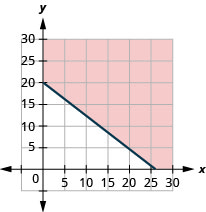
ⓐ\(10x+13y\geq 260\)
ⓑ
ⓒ 答案会有所不同。
维罗妮卡从事两份兼职工作,以便赚到足够的钱来履行每周至少280美元的义务。 她在日间水疗中心的工作每小时支付10美元,而她在校园的行政助理工作每小时支付17.50美元。 维罗妮卡每份工作需要工作多少小时才能赚到至少280美元?
ⓐ 让 x 成为她在日间水疗中心工作的小时数,让 y 成为她担任行政助理的小时数。 写一个不等式来模拟这种情况。
ⓑ 绘制不等式图。
ⓒ 找到三个可以解决不等式的有序对(x,y)。 然后,解释一下这对维罗妮卡意味着什么
- 回答
-
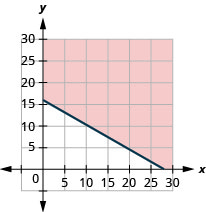
ⓐ\(10x+17.5y\geq 280\)
ⓑ
ⓒ 答案会有所不同。
访问此在线资源,获取更多指导和练习,在两个变量中绘制线性不等式。
关键概念
- 如何在两个变量中绘制线性不等式。
- 识别边界线并绘制图表。
如果不等式为\(\leq\)或\(\geq\),则边界线为实线。
如果不等式为\(<\)或\(>\),则边界线为虚线。 - 测试不在边界线上的点。 这是不平等的解决方案吗?
- 边界线一侧的阴影。
如果测试点是解,则在包含该点的一侧加上阴影。
如果测试点不是解决方案,则在另一侧遮阳。
- 识别边界线并绘制图表。
词汇表
- 边界线
- 带方程的直线\(Ax+By=C\)是分隔区域与所在\(Ax+By>C\)区域的边界线\(Ax+By<C\)。
- 线性不等式
- 线性不等式是一种可以用以下形式之一书写的不等式:\(Ax+By>C\)、\(Ax+By\geq C\)\(Ax+By<C\)\(Ax+By\leq C\)、或,其中 A 和 B 不都为零。
- 线性不等式的解
- 当我们替换 x 和 y 的值时,如果不等式为真,则有序对\((x,y)\)是线性不等式的解。


