3.3E：练习

Last updated
Save as PDF

Page ID: 203870

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

练习成就完美

找出直线的斜率

在以下练习中，找到所示每条线的斜率。

1。
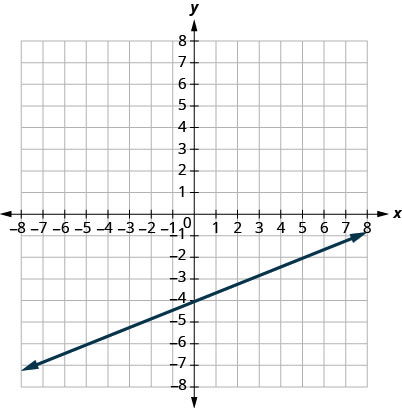
$此图显示了 x y 坐标平面上的一条直线的图形。 x 轴的长度从负 8 到 8。 y 轴的长度从负 8 到 8。直线穿过点（0，负 4）和（5，负 2）。$

回答: $m=\frac{2}{5}$

2。
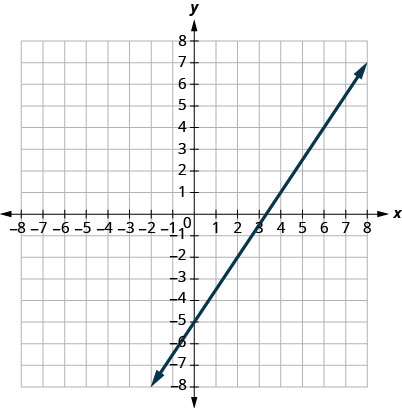
$此图显示了 x y 坐标平面上的一条直线的图形。 x 轴的长度从负 8 到 8。 y 轴的长度从负 8 到 8。直线穿过点（0，负 5）和（2，负 2）。$

3。
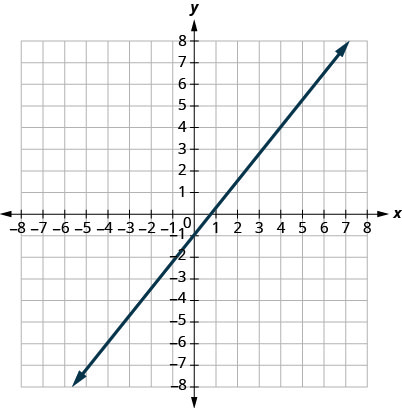
$此图显示了 x y 坐标平面上的一条直线的图形。 x 轴的长度从负 8 到 8。 y 轴的长度从负 8 到 8。直线穿过点（0，负 1）和（4，4）。$

回答: $m=\frac{5}{4}$

4。
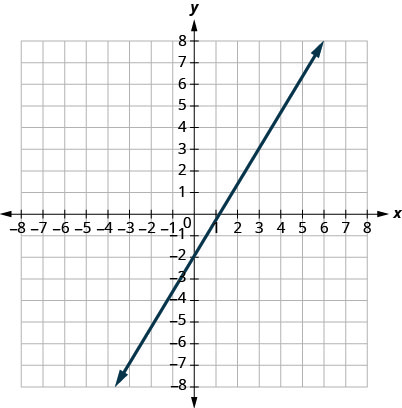
$此图显示了 x y 坐标平面上的一条直线的图形。 x 轴的长度从负 8 到 8。 y 轴的长度从负 8 到 8。直线穿过点（0，负 2）和（3，3）。$

5。
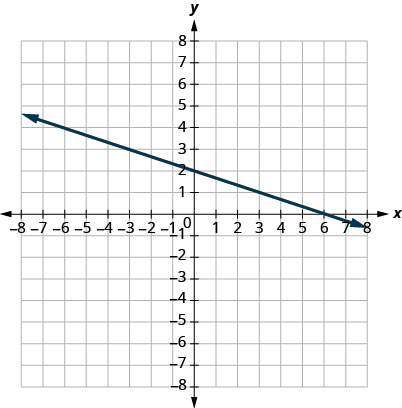
$此图显示了 x y 坐标平面上的一条直线的图形。 x 轴的长度从负 8 到 8。 y 轴的长度从负 8 到 8。直线穿过点 (0, 2) 和 (3, 1)。$

回答: $m = -\frac{1}{3}$

6。
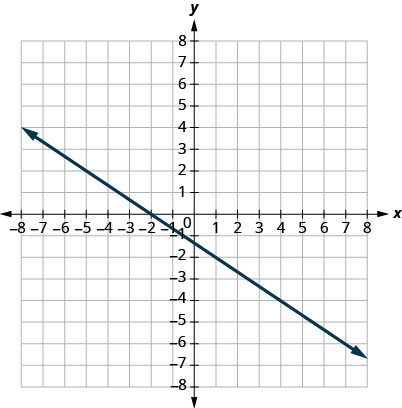
$此图显示了 x y 坐标平面上的一条直线的图形。 x 轴的长度从负 8 到 8。 y 轴的长度从负 8 到 8。直线穿过点（0，负 1）和（3，负 3）。$

7。
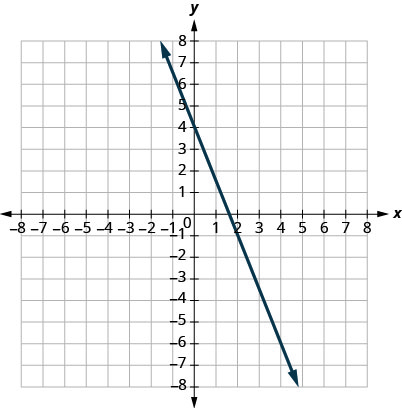
$此图显示了 x y 坐标平面上的一条直线的图形。 x 轴的长度从负 8 到 8。 y 轴的长度从负 8 到 8。直线穿过点 (0, 4) 和 (2, 负 1)。$

回答: $m = -\frac{5}{2}$

8。
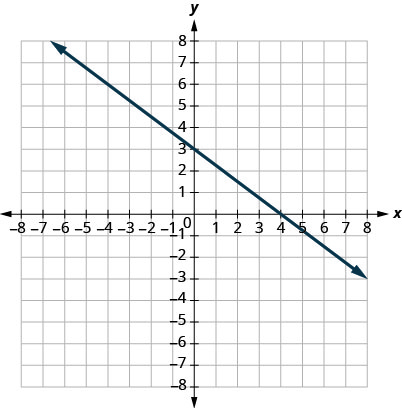
$此图显示了 x y 坐标平面上的一条直线的图形。 x 轴的长度从负 8 到 8。 y 轴的长度从负 8 到 8。直线穿过点 (0, 2) 和 (4, 负 1)。$

在以下练习中，找出每条线的斜率。

9。 $y=3$

回答: $m = 0$

10。 $y=−2$

11。 $x=−5$

回答: 未定义

12。 $x=4$

在以下练习中，使用斜率公式求出每对点之间的直线的斜率。

13。 $(2,5),\;(4,0)$

回答: $m = -\frac{5}{2}$

14。 $(3,6),\;(8,0)$

15。 $(−3,3),\;(4,−5)$

回答: $m = -\frac{8}{7}$

16。 $(−2,4),\;(3,−1)$

17。 $(−1,−2),\;(2,5)$

回答: $m = \frac{7}{3}$

18。 $(−2,−1),\;(6,5)$

19。 $(4,−5),\;(1,−2)$

回答: $m = -1$

20。 $(3,−6),\;(2,−2)$

给定一个点和斜率绘制一条直线

在以下练习中，用给定的点和斜率绘制每条线的图形。

21。 $(2,5)$;$m=−\frac{1}{3}$

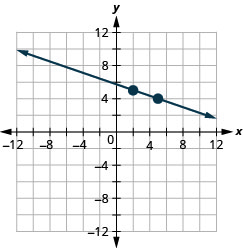
回答: $此图显示了 x y 坐标平面上的一条直线的图形。 x 轴的长度从负 12 到 12。 y 轴从负 12 延伸到 12。直线穿过点 (2、5) 和 (5、4)。$

22。 $(1,4)$;$m=−\frac{1}{2}$

23。 $(−1,−4)$;$m=\frac{4}{3}$

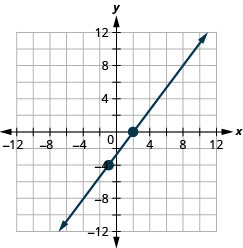
回答: $此图显示了 x y 坐标平面上的一条直线的图形。 x 轴的长度从负 12 到 12。 y 轴从负 12 延伸到 12。直线穿过点（负 1、负 4）和（2、0）。$

24。 $(−3,−5)$;$m=\frac{3}{2}$

25。 $y$-截距:$(0, 3)$;$m=−\frac{2}{5}$

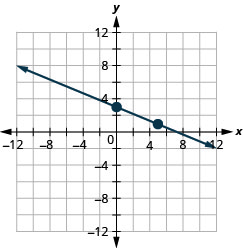
回答: $此图显示了 x y 坐标平面上的一条直线的图形。 x 轴的长度从负 12 到 12。 y 轴从负 12 延伸到 12。直线穿过点 (0, 3) 和 (5, 1)。$

26。 $x$-截距:$(−2,0)$;$m=\frac{3}{4}$

27。 $(−4,2)$;$m=4$

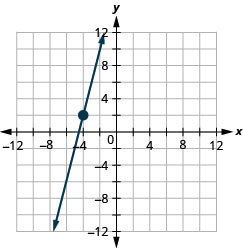
回答: $此图显示了 x y 坐标平面上的一条直线的图形。 x 轴的长度从负 12 到 12。 y 轴从负 12 延伸到 12。直线穿过点（负 4、2）和（负 3、6）。$

28。 $(1,5)$;$m=−3$

使用斜率和截距绘制直线图

在以下练习中，确定每条线的斜率和 y 截距。

29。 $y=−7x+3$

回答: $m=−7$;$(0,3)$

30。 $y=4x−10$

31。 $3x+y=5$

回答: $m=−3$;$(0,5)$

32。 $4x+y=8$

33。 $6x+4y=12$

回答: $m=−\frac{3}{2}$;$(0,3)$

34。 $8x+3y=12$

35。 $5x−2y=6$

回答: $m=\frac{5}{2}$;$(0,−3)$

36。 $7x−3y=9$

在以下练习中，使用每个方程的斜率和 y 截距绘制每个方程的直线。

37。 $y=3x−1$

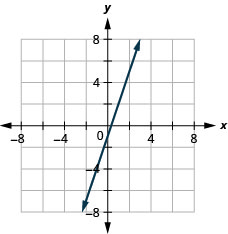
回答: $此图显示了 x y 坐标平面上的一条直线的图形。 x 轴的范围从负 10 到 10。 y 轴的长度从负 10 到 10。直线穿过点（0，负 1）和（1，2）。$

38。 $y=2x−3$

39。 $y=−x+3$

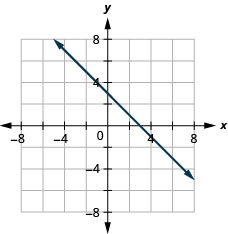
回答: $此图显示了 x y 坐标平面上的一条直线的图形。 x 轴的范围从负 10 到 10。 y 轴的长度从负 10 到 10。直线穿过点 (0, 3) 和 (1, 2)。$

40。 $y=−x−4$

41。 $y=−\frac{2}{5}x−3$

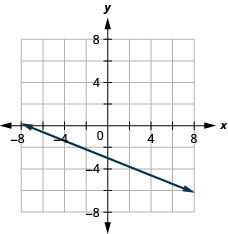
回答: $此图显示了 x y 坐标平面上的一条直线的图形。 x 轴的范围从负 10 到 10。 y 轴的长度从负 10 到 10。直线穿过点（0，负 3）和（5，负 5）。$

42。 $y=−\frac{3}{5}x+2$

43。 $3x−2y=4$

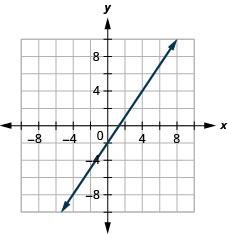
回答: $此图显示了 x y 坐标平面上的一条直线的图形。 x 轴的范围从负 10 到 10。 y 轴的长度从负 10 到 10。直线穿过点（0，负 2）和（2，1）。$

44。 $3x−4y=8$

选择最方便的方法来绘制线条

在以下练习中，确定绘制每条线的最便捷方法。

45。 $x=2$

回答: 垂直线

46。 $y=5$

47。 $y=−3x+4$

回答: 斜率截距

48。 $x−y=5$

49。 $x−y=1$

回答: 截住

50。 $y=\frac{2}{3}x−1$

51。 $3x−2y=−12$

回答: 截住

52。 $2x−5y=−10$

绘制和解释坡度截距的应用

53。该方程$P=31+1.75w$模拟了 Tuyet 每月支付的水费账单（以美元为单位）与所用水单位数量之间的关系。$P$$w$

a. 找出 Tuyet 在使用$0$单位用水时支付的一个月的报酬。

b. 找到 Tuyet 在使用$12$单位用水时支付的一个月的报酬。

c. 解释方程的斜率和$P$截距。

d. 绘制方程图。

回答

a.$$31$
b.$$52$
c. 斜率表示当用水单位数增加$$1.75$时$P$$w$，补助金将增加$1$。$1.75$ $P$-intercept 表示，当 Tuyet 使用的水单位数为时$0$，付款为$$31$。
d。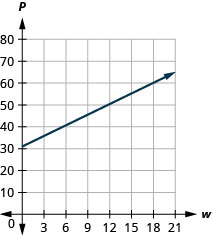

$此图显示了 x y 坐标平面上的一条直线的图形。 x 轴从负 1 延伸到 21。 y 轴的范围从负 1 到 80。直线穿过点 (0、31) 和 (12、52)。$

54。该方程$P=28+2.54w$模拟了兰迪每月支付的水费账单金额（以美元计）与所用水单位数之间的关系。$P$$w$

a. 找到 Randy 使用$0$单位水时一个月的报酬。

b. 找到 Randy 使用$15$单位水时一个月的报酬。

c. 解释方程的斜率和$P$截距。

d. 绘制方程图。

55。布鲁斯为工作开车。该方程$R=0.575m+42$模拟了他获得报销的美元金额与他一天内行驶的里程数之间的关系。$R$$m$

a. 找出 Bruce 在行驶$0$里程的当天获得的补偿金额。

b. 找出 Bruce 在行驶$220$里程的当天获得的补偿金额。

c. 解释方程的斜率和$R$截距。

d. 绘制方程图。

回答

a.$$42$
b.$$168.50$
c. 斜率$0.575$意味着他获得的补偿金额随着行驶里程数的增加而增加$1$。$R$$$0.575$$m$ $R$-intercept 表示当行驶里程数为时$0$，报销金额为$$42$。
d。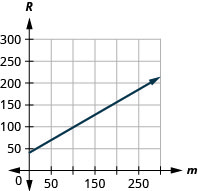

$此图显示了 x y 坐标平面上的一条直线的图形。 x 轴的长度从负 50 到 250。 y 轴的长度从负 50 到 300。这条线穿过点 (0、42) 和 (220、168.5)。$

56。珍妮尔计划在度假时租车。该方程$C=0.32m+15$模拟了以美元为单位的每日成本与她一天内行驶的里程数之间的关系。$C$$m$

a. 找出 Janelle 有一天能开车$0$里程的成本。

b. 找出 Janelle 开车$400$里程的那一天的成本。

c. 解释方程的斜率和$C$截距。

d. 绘制方程图。

57。 Cherie从事零售业，她的周薪包括她销售金额的佣金。该方程$S=400+0.15c$模拟了她的周薪（以美元为单位）与销售额（以美元为单位）之间的关系。$S$$c$

a. 查一下 Cherie 一周的销售额为止的薪水$$0$。

b. 查看 Cherie 一周的销售额达到时的工资$$3,600$。

c. 解释方程的斜率和$S$截距。

d. 绘制方程图。

回答

a.$$400$
b.$$940$
c. 斜率意味$0.15$着 Cherie 的薪水 S 每$$1$增加一次销售额就会增加。$$0.15$ $S$-intercept 表示当她的销售额达到时$$0$，她的薪水就是$$400$。
d。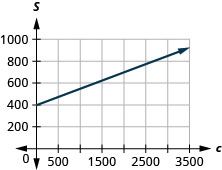

$此图显示了 x y 坐标平面上的一条直线的图形。 x 轴从负 500 延伸到 3500。 y 轴的长度从负 200 到 1000。这条线穿过点 (0, 400) 和 (3600, 940)。$

58。帕特尔的周薪包括基本工资和销售佣金。该方程$S=750+0.09c$模拟了他的周薪（以美元计）与销售额（以美元计）之间的关系。$S$$c$

a. 找出帕特尔一周的销售额为止的工资$0$。

b. 找出帕特尔一周的销售额为止的工资$18,540$。

c. 解释方程的斜率和$S$截距。

d. 绘制方程图。

59。科斯塔正计划举行午餐宴会。该方程$C=450+28g$模拟了以美元为单位的宴会费用与客人人数之间的关系$g$。$C$

a. 如果房客数量为，则找出费用$40$。

b. 如果房客人数为，则查找费用$80$。

c. 解释方程的斜率和$C$截距。

d. 绘制方程图。

回答

a.$$1570$
b.$$5690$
c. 斜率给出了每位客人的费用。斜率表示当房客数量增加$$28$时$C$，成本会增加$1$。$28$ $C$-intercept 表示，如果房客数量为$0$，则费用为$$450$。
d。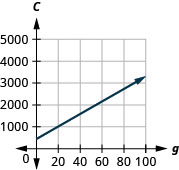

$此图显示了 x y 坐标平面上的一条直线的图形。 x 轴的长度从负 20 到 100。 y 轴的长度从负 1000 到 7000。这条线穿过点 (0, 450) 和 (40, 1570)。$

60。玛吉正在计划一场晚宴。该方程$C=750+42g$模拟了以美元为单位的宴会费用与客人人数之间的关系$g$。$C$

a. 如果房客数量为，则找出费用$50$。

b. 如果房客人数为，则查找费用$100$。

c. 解释方程的斜率和$C$截距。

d. 绘制方程图。

使用斜率识别平行线和垂直线

在以下练习中，使用斜率和$y$截距来确定两条线是平行、垂直还是两者都不平行。

61。 $y=\frac{3}{4}x−3$;$3x−4y=−2$

回答: 平行

62。 $3x−4y=−2$;$y=\frac{3}{4}x−3$

63。 $2x−4y=6$;$x−2y=3$

回答: 也不

64。 $8x+6y=6$;$12x+9y=12$

65。 $x=5$;$x=−6$

回答: 平行

66。 $x=−3$;$x=−2$

67。 $4x−2y=5$;$3x+6y=8$

回答: 垂直

68。 $8x−2y=7$;$3x+12y=9$

69。 $3x−6y=12$;$6x−3y=3$

回答: 也不

70。 $9x−5y=4$;$5x+9y=−1$

71。 $7x−4y=8$;$4x+7y=14$

回答: 垂直

72。 $5x−2y=11$;$5x−y=7$

73。 $3x−2y=8$;$2x+3y=6$

回答: 垂直

74。 $2x+3y=5$;$3x−2y=7$

75。 $3x−2y=1$;$2x−3y=2$

回答: 也不

76。 $2x+4y=3$;$6x+3y=2$

77。 $y=2$;$y=6$

回答: 平行

78。 $y=−1$;$y=2$

写作练习

79。带斜率的直线的图形与带斜率的直线的图形有$m=12$何不同$m=2$？

回答: 答案会有所不同。

80。为什么垂直线的斜率 “未定义”？

81。解释如何绘制给定点及其斜率的直线。

回答: 答案会有所不同。

82。用你自己的话解释如何决定使用哪种方法来绘制线条。

自检

a. 完成练习后，使用此清单评估您对本节目标的掌握程度。

$此表有 7 行和 4 列。第一行是标题行，它标记每列。第一列标题是 “我能...”，第二列是 “自信地”，第三列是 “有帮助”，第四列是 “不，我不明白”。第一列下方是 “找到直线的斜率”、“给定点和斜率绘制一条线”、“使用斜率和截距绘制直线”、“选择最方便的方法绘制直线”、“绘制和解释斜率截距的应用” 以及 “使用斜率识别平行线和垂直线”。其他栏留空，以便学员可以指明他们对每个主题的掌握程度。$

b. 看完这份清单后，你会怎么做才能对所有目标充满信心？