2.5：求解混合和均匀运动应用程序

学习目标

在本节结束时，您将能够：

• 解决硬币字问题
• 解决票证和邮票字词问题
• 解决混词问题
• 解决均匀运动应用程序

在开始之前，请参加这个准备测验。

1. 简化：\(0.25x+0.10(x+4)\)。
   如果你错过了这个问题，请查看 [链接]。
2. 成人票的数量是三张，是儿童票数量的两倍多。 让 c 表示儿童票的数量。 为成人票的数量写一个表达式。
   如果你错过了这个问题，请查看 [链接]。
3. 将 4.2% 转换为十进制。
   如果你错过了这个问题，请查看 [链接]。

解决硬币单词问题

用代数来找出存钱罐中的镍和便士的数量可能看起来很愚蠢。 你可能想知道为什么我们不开银行然后数钱。 但是这种问题向我们介绍了一些技巧，这些技巧在我们继续数学研究时会很有用。

如果我们有一大笔钱，我们将如何确定它的价值？ 如果我们计算一角钱，我们就会知道我们有多少毛钱——一角钱。 但这并不能告诉我们所有硬币的价值。 假设我们数了23毛钱，它们值多少钱？ 每角钱价值0.10美元，相当于一角钱的价值。 要得出这堆23毛钱的总价值，请将23乘以0.10美元得出2.30美元。

角钱数乘以每角钱的价值等于一角钱的总价值。

\[\begin{align} \textit{number}·\textit{value} &= \textit{total value} \nonumber\\ 23·$0.10 &= $2.30 \nonumber\\ \end{align} \nonumber\]

此方法得出以下模型。

硬币的总价值

对于相同类型的硬币，许多硬币的总价值是通过使用模型得出的

\[\textit{number}·\textit{value}=\textit{total value} \nonumber \]

• 数字是硬币的数量
• 价值是每枚硬币的价值
• 总价值是所有硬币的总价值

如果我们有几种类型的硬币，我们可以继续对每种类型的硬币进行此处理，然后我们就会知道每种硬币的总价值。 要获得所有硬币的总价值，请将每种硬币的总价值相加。

示例\(\PageIndex{1}\)

杰西的存钱罐里有价值3.02美元的便士和镍。 镍的数量是便士数量的八倍以上的三倍。 杰西有多少镍和多少便士？

回答

第 1 步。 阅读问题。 确定所涉及的硬币类型。 创建表。 写下每种硬币的价值。	便士和镍 便士价值0.10美元。 镍的价值为0.05美元。
第 2 步。 确定我们在寻找什么。	便士和镍的数量
第 3 步。 姓名。 使用变量表示每种硬币的数量。 镍的数量是根据便士的 数量来定义的，所以从便士开始。 镍的数量是便士数量的八倍 以上的三倍。	让\(p=\)数便士。 \(8p+3=\)镍的数量
在图表中，将数字和值相乘 得出每种硬币的总价值。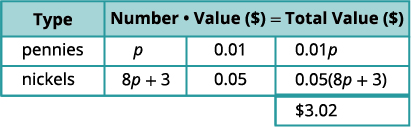
第 4 步。 翻译。 通过将所有类型硬币的总价值相加来写出方程式。
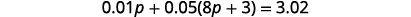
第 5 步。 求解方程。
多少镍？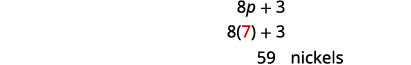
第 6 步。 检查问题中的答案并确保答案合理。 杰西有 7 便士和 59 个镍。 是总价值\($3.02\)吗？ \(\begin{align} 7(0.01)+59(0.05) &\overset{?}{=} 3.02 \nonumber \\ 3.02 &= 3.02\checkmark \nonumber \\ \end{align}\)

示例\(\PageIndex{2}\)

杰西口袋里有价值6.55美元的季度和镍。 镍的数量是四分之一数的两倍以上的五个。 杰西有多少镍和多少个季度？

回答

杰西有 41 个镍和 18 个季度。

示例\(\PageIndex{3}\)

Elane 的硬币罐里总共有 7.00 美元的毛钱和镍。 Elane 拥有的硬币数量比镍的三倍少了七角钱。 Elane 每枚硬币有多少枚？

回答

Elane 有 22 个镍和 59 角钱。

解决硬币字问题的步骤总结如下。

解决硬币字问题。

1. 阅读问题。 确保所有文字和想法都被理解。
   • 确定所涉及的硬币类型。
   • 创建一个表来组织信息。
     • 将列标记为 “类型”、“数字”、“值” 和 “总值”。
     • 列出硬币的类型。
     • 写下每种硬币的价值。
     • 写下所有硬币的总价值。
     • 
2. 确定你在找什么。
3. 说出你要找的东西。 选择一个变量来表示该数量。
   • 使用变量表达式表示每种硬币的数量并将其写入表中。
   • 将数字乘以该值得出每种硬币的总价值。
4. 翻译成方程式。
   • 用一句话用所有重要信息重述问题可能会有所帮助。 然后，将句子翻译成方程式。
   • 通过将所有类型硬币的总值相加来写出方程式。
5. 使用良好的代数技巧求@@ 解方程。
6. 检查问题中的答案并确保答案合理。
7. 用完整的句子@@ 回答问题。

解决票证和邮票字词问题

涉及门票或邮票的问题很像硬币问题。 每种类型的票证和邮票都有价值，就像每种硬币一样。 因此，为了解决这些问题，我们将遵循与解决硬币问题相同的步骤。

示例\(\PageIndex{4}\)

丹尼花了15.75美元买了邮票。 49美分邮票的数量比35美分邮票数量少了五倍。 丹尼买了多少张 49 美分的邮票和多少 35 美分的邮票？

回答

第 1 步。 确定所涉及的邮票类型。	49 美分的邮票和 35 美分的邮票
第 2 步。 确定我们正在寻找的。	49 美分邮票的数量和 35 美分邮票的数量
第 3 步。 编写变量表达式来表示每种类型邮票的数量。	假设 x = 35 美分邮票的数量。
“49美分邮票的数量 比35美分邮 票数量少了五倍。”	3x−5=3x−5= 49 美分邮票的数量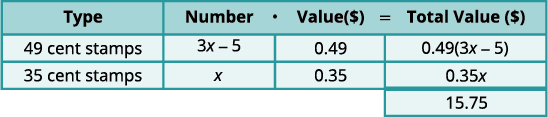
第 4 步。 从总值中写出方程。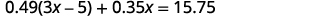
第 5 步。 求解方程。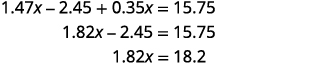
有多少 49 美分的邮票？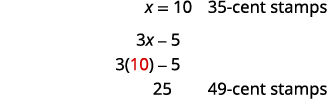
第 6 步。 查看。 10 (0.35) +25 (0.49) 3.50+12.2515.75=？ =？ =15.7515.7515.75 ✓ 10 (0.35) +25 (0.49) =？ 15.753.50+12.25=？ 15.7515.75=15.75 ✓
第 7 步。 用完整的句子回答问题。	丹尼买了十张 35 美分的邮票和二十五张 49 美分的邮票。

示例\(\PageIndex{5}\)

埃里克花了19.88美元购买了邮票。 49美分邮票的数量为八张，是35美分邮票数量的两倍多。 埃里克买了多少张 49 美分的邮票和多少张 35 美分的邮票？

回答

埃里克买了三十二张 49 美分的邮票和十二张 35 美分的邮票。

示例\(\PageIndex{6}\)

Kailee 花了 14.74 美元购买了邮票。 49美分邮票的数量比20美分邮票数量少了四倍。 凯莉买了多少张 49 美分的邮票和多少 20 美分的邮票？

回答

凯莉购买了二十六张 49 美分的邮票和十张 20 美分的邮票。

到目前为止，在我们的大多数例子中，我们都被告知一个数量是另一个数量的两倍或相似的四个。 在下一个示例中，我们必须以不同的方式关联数量。

假设 Aniket 总共售出了 100 张门票。 每张票要么是成人票，要么是儿童票。 如果他卖了20张儿童票，他卖了多少张成人票？

你刚才说 “80”？ 你是怎么知道的？ 你从 100 中减去了 20 吗？

如果他卖了 45 张儿童票，那么他卖了多少张成人票？

你刚才说 “55”？ 你是怎么找到的？ 从 100 中减去 45？

现在，假设 Aniket 售出了 x 张儿童票。 那他卖了多少张成人票？ 为了找出答案，我们将遵循上面使用的相同逻辑。 在每种情况下，我们从 100 张中减去儿童票的数量得出成人票的数量。 我们现在对 x 做同样的事情。

我们在表中对此进行了总结。

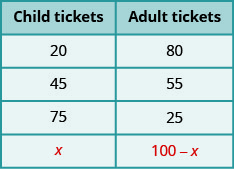
我们将在下一个示例中应用此技术。

示例\(\PageIndex{7}\)

一艘观鲸船上有 40 名付费乘客。 从门票中获得的总收入为1,196美元。 全价乘客每人支付32美元，减价乘客每人支付26美元。 船上有多少全价乘客和多少减价乘客？

回答

第 1 步。 确定涉及的门票类型。	全价机票和减价机票
第 2 步。 确定我们在寻找什么。	全价机票和减价机票的数量
第 3 步。 姓名。 使用变量表示每种类型的票证的数量。	假设 f = 全价票的数量。 40−f=40−f= 减价机票的数量
我们知道售出的门票总数为40张。 这意味着减价机票的数量减去全价机票数量的40张。 将数字乘以该值得出每种类型票证的总价值。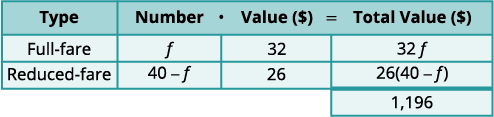
第 4 步。 翻译。 通过将每种类型的票证的总值相加来写出方程式。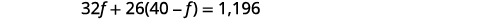
第 5 步。 求解方程。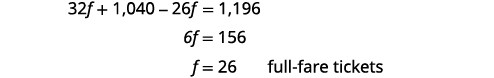
减价了多少？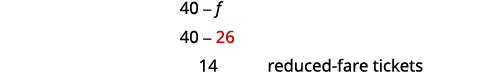
第 6 步。 检查答案。 有26张全价机票，每张32美元，14张减价票，每张26美元。 总价值是116美元吗？ 26·3214·26==832364——1,196 ✓ 26·32=83214·26=364——1,196 ✓
第 7 步。 回答问题。	他们售出了26张全价票和14张减价票。

示例\(\PageIndex{8}\)

在博物馆售票亭轮班期间，莉亚售出了115张门票，总额为1,163美元。 成人票价格为12美元，学生票为5美元。 Leah 卖了多少张成人票和多少张学生票？

回答

84 张成人票，31 张学生票

示例\(\PageIndex{9}\)

盖伦售出了810张教堂狂欢节门票，总收入为2,820美元。 儿童票每张3美元，成人票每张5美元。 他卖了多少张儿童票和多少张成人票？

回答

615 张儿童票和 195 张成人票

解决混词问题

现在，我们将解析混料模型的一些更常见的应用。 在混合物问题中，我们经常混合两种量，例如葡萄干和坚果，以制成混合物，例如混合物。 在我们的表格中，我们将为要混合的每种物品排成一行，最后的混合物也有一行。

示例\(\PageIndex{10}\)

Henning 正在混合葡萄干和坚果，制成 25 磅的混合物。 葡萄干的价格为每磅4.50美元，坚果的价格为每磅8美元。 如果亨宁想把混合葡萄干的成本定为每磅6.60美元，那么他应该用多少磅的葡萄干和多少磅的坚果？

回答

第 1 步。 确定混合了什么。	25 磅的混合物将来自葡萄干和坚果的混合。
第 2 步。 确定我们在寻找什么。	葡萄干和坚果的磅数
第 3 步。 使用变量表示每种类型的票证的数量。 和以前一样，我们填写一张图表来整理我们的信息。 我们输入每件商品的每磅价格。 我们将数字乘以该值得出总值。	假设 x=x= 葡萄干的磅数。 25−x=25−x= 坚果的磅数
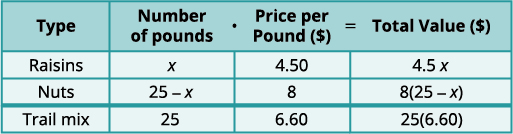
请注意，表中的最后一 列提供了 混合物总量的信息。
第 4 步。 翻译成方程式。	葡萄干的价值加上坚果的价值将是 混合葡萄干的价值。
第 5 步。 求解方程。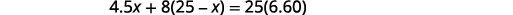
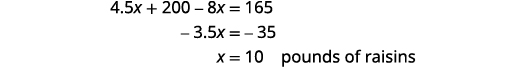
找出坚果的磅数。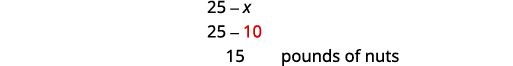
第 6 步。 查看。 4.5 (10) +8 (15) 45+120165=？ =？ =25 (6.60) 165165 ✓ 4.5 (10) +8 (15) =？ 25 (6.60) 45+120=？ 165165=165 ✓
第 7 步。 回答问题。	亨宁将十磅的葡萄干和15磅的坚果混合在一起。

示例\(\PageIndex{11}\)

奥兰多正在混合坚果和麦片方块来制作派对混合物。 坚果的售价为每磅7美元，谷物方块的售价为每磅4美元。 奥兰多想以每磅 6.50 美元的价格制作 30 磅的派对混合物，他应该用多少磅的坚果和多少磅的麦片方块？

回答

奥兰多混合了五磅的谷物方块和25磅的坚果。

示例\(\PageIndex{12}\)

Becca 想混合果汁和苏打水来打一拳。 她可以以每加仑3美元的价格购买果汁，以每加仑4美元的价格购买苏打水。 如果她想以每加仑3.25美元的价格制作28加仑的拳头，那么她应该买多少加仑的果汁和多少加仑的苏打水？

回答

Becca 混合了 21 加仑的水果拳和七加仑的苏打水。

求解均匀运动应用程序

当你使用巡航控制系统沿着州际公路行驶时，你的汽车的速度保持不变，它是统一的。 我们将物体速度恒定的问题称为均匀运动应用程序。 我们将使用距离、速率和时间公式来比较两种情况\(D=rt\)，例如两辆车以不同的速率或相反的方向行驶。

我们的问题解决策略在这里仍然适用，但我们将增加第一步。 第一步将包括绘制一张示意图，显示示例中发生的情况。 绘制图表可以帮助我们了解正在发生的事情，这样我们就可以写出一个合适的方程式。 然后，我们将制作一张表格来整理信息，就像我们在硬币、门票和邮票申请中所做的那样。

此处列出了这些步骤以便于参考：

求解均匀运动应用程序。

1. 阅读问题。 确保所有文字和想法都被理解。
   • 画一张图来说明正在发生的事情。
   • 创建一个表来组织信息。
     • 标注速率、时间、距离列。
     • 列出两个场景。
     • 写下你知道的信息。
   
2. 确定你在找什么。
3. 说出你要找的东西。 选择一个变量来表示该数量。
   • 完成图表。
   • 使用变量表达式表示每行中的该数量。
   • 将速率乘以时间得出距离。
4. 翻译成方程式。
   • 用一句话用所有重要信息重述问题。
   • 然后，将句子翻译成方程式。
5. 使用良好的代数技巧求@@ 解方程。
6. 检查问题中的答案并确保答案合理。
7. 用完整的句子@@ 回答问题。

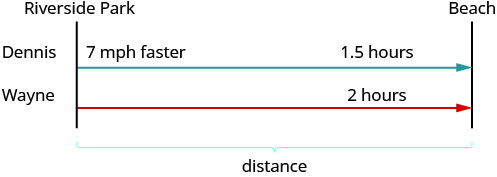
韦恩和丹尼斯喜欢骑自行车从河滨公园到海滩。 丹尼斯的速度比韦恩的速度快七英里/小时，因此韦恩骑车到海滩需要两个小时，而丹尼斯则需要1.5个小时才能骑行。 找出两个骑自行车的人的速度。

回答

第 1 步。 阅读问题。 确保所有文字和想法都被理解。

画一张图来说明发生了什么。 下图是示例中发生的事情的草图。

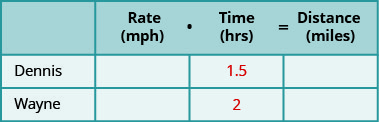
创建一个表来组织信息。

• 将列标记为 “速率”、“时间” 和 “距离”。
• 列出两个场景。
• 写下你知道的信息。
  

第 2 步。 确定你在找什么。

你被要求找出两个骑自行车的人的速度。

请注意，距离公式使用 “速率” 一词，但更常见的是使用 “速度”

当我们用日常英语谈论车辆时。

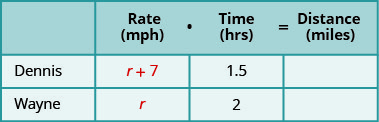
第 3 步。 说出我们要找的东西。 选择一个变量来表示该数量。

完成图表使用变量表达式表示每行中的数量。
我们正在寻找骑自行车的人的速度。 让我们让 r 表示 Wayne 的速度。 由于丹尼斯的速度快了7英里/小时，因此我们将其表示为在图表中\(r+7\)
\(\begin{align} r+7 &= \text{Dennis’ speed} \nonumber \\ r &= \text{Wayne’s speed} \nonumber \\ \end{align}\)
填写速度。

将速率乘以时间得出距离。

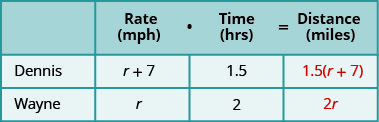
第 4 步。 翻译成方程式。

用一句话用所有重要信息重述问题。

然后，将句子翻译成方程式。
对这种情况进行建模的方程将来自距离之间的关系。 看看我们上面画的图。 丹尼斯的行驶距离与韦恩的行驶距离有何关系？
由于两个骑自行车的人都从河滨出发，前往海滩，因此他们的行驶距离相同。 所以我们这样写：

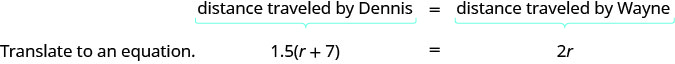
第 5 步。 使用代数技术求解方程。

现在求解这个方程。	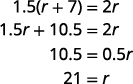所以 Wayne 的速度是 21 英里/小时。
找出丹尼斯的速度。	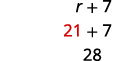丹尼斯的速度 28 英里每小时。

第 6 步。 检查问题中的答案并确保答案合理。

\(\begin{align} \text{} &{28\text{ mph}(1.5\text{ hours}) } &= {42\text{ miles}\checkmark} \nonumber \\ \text{} &{21\text{ mph}(2\text{ hours})} &= {42\text{ miles}\checkmark} \nonumber \\ \end{align} \)

第 7 步。 用完整的句子回答问题。

韦恩以每小时 21 英里的速度骑行，丹尼斯以 28 英里/小时的速度骑行

用一句话用所有重要信息重述问题。

然后，将句子翻译成方程式。
对这种情况进行建模的方程将来自距离之间的关系。 看看我们上面画的图。 丹尼斯的行驶距离与韦恩的行驶距离有何关系？
由于两个骑自行车的人都从河滨出发，前往海滩，因此他们的行驶距离相同。 所以我们这样写：

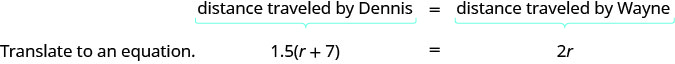
特@@ 快列车和当地火车离开匹兹堡前往华盛顿特区。特快列车可以在四个小时内出行，而当地火车则需要五个小时才能到达。 特快列车的速度比当地列车的速度快12英里/小时。 找出两列火车的速度。

回答

当地列车的速度为48英里/小时，特快列车的速度为60英里/小时。

示例\(\PageIndex{15}\)

杰罗米可以在4.5小时内从他在克利夫兰的家中开车到他在芝加哥的大学。 他妈妈要花六个小时才能开同样的车。 杰罗米每小时的行驶速度比他母亲快 20 英里。 找出杰罗米的速度和他母亲的速度。

回答

杰罗米以 80 英里/小时的速度开车，他的母亲开了 60 英里/小时。

在示例中，我们有两个骑自行车的人行驶相同的距离。 在下一个示例中，两个人互相开车直到相遇。

示例\(\PageIndex{16}\)

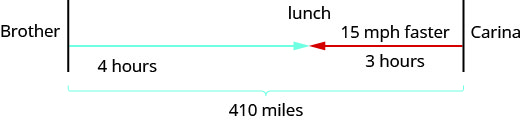
在她哥哥从伯克利开车去阿纳海姆的同一天，Carina正从阿纳海姆的家中开车去伯克利，所以他们决定沿途在Buttonwillow见面吃午饭。 从阿纳海姆到伯克利的距离为 395 英里。 Carina 花了三个小时才到达 Buttonwillow，而她的兄弟开车四个小时才能到达。 Carina 的平均时速比她哥哥的平均速度快 15 英里/小时。 找出 Carina 和她兄弟的平均速度。

回答

第 1 步。 阅读问题。 确保所有文字和想法都被理解。

画一张图来说明发生了什么。 下面显示了示例中正在发生的事情的草图。

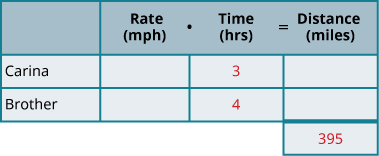
创建一个表来组织信息。

• 标注速率、时间、距离列。
• 列出两个场景。
• 写下你知道的信息。
  

第 2 步。 确定我们在寻找什么。

我们被要求找出 Carina 和她兄弟的平均速度。

第 3 步。 说出我们要找的东西。 选择一个变量来表示该数量。

完成图表。 使用变量表达式表示每行中的该数量。
我们正在寻找他们的平均速度。 让我们让 r 表示 Carina 的平均速度。 由于兄弟的速度快了15英里/小时，我们将其表示为\(r+15\)。
在图表中填写速度。 将速率乘以时间得出距离。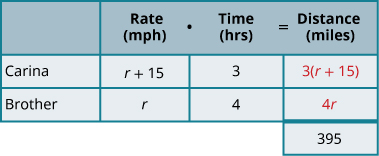

第 4 步。 翻译成方程式。

用一句话用所有重要信息重述问题。 然后，将句子翻译成方程式。
同样，我们需要确定距离之间的关系才能写出方程。 看看我们在上面绘制的图表，注意一下 Carina 走过的距离和她哥哥走过的距离之间的关系。
Carina 走过的距离加上她哥哥的行驶距离加起来必须等于 410 英里。 所以我们这样写：

第 5 步。 使用代数技术求解方程。

现在求解这个方程。	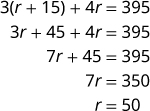所以 Carina 兄弟的速度是 50 英里/小时。
Carina 的速度是 r+15.r+15。	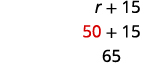她哥哥的速度是 65 英里/小时。

第 6 步。 检查问题中的答案并确保答案合理。

\(\begin{array} {llll} \text{Carina drove} &{65\text{ mph}(3\text{ hours})} &= &{\underline{195 \text{ miles}}} \\ \text{Her brother drove} &{50\text{ mph}(4\text{ hours})} &= &{\underline{200 \text{ miles}}} \\ {} &{} &{} &{395\text{ miles}\checkmark} \\ \end{array} \)

第 7 步。 用完整的句子回答问题。

Carina 开了 65 英里/小时，她的兄弟开了 50 英里/小时。

我以 80 英里/小时的速度开车，他妈妈开了 60 英里/小时。

示例\(\PageIndex{17}\)

克里斯托弗和他的父母相隔115英里。 他们在家中的一家餐馆见面，庆祝他母亲的生日。 克里斯托弗开车一个半小时，而他的父母开车一个小时去餐厅。 克里斯托弗的平均速度比他父母的平均速度快十英里/小时。 克里斯托弗和他的父母开车去餐厅时的平均速度是多少？

回答

克里斯托弗的速度是 50 英里/小时，他父母的速度是 40 英里/小时。

示例\(\PageIndex{18}\)

阿什利在明尼阿波利斯上大学，距离她在苏福尔斯的家234英里。 她希望父母给她带更多的冬装，所以他们决定在明尼阿波利斯和苏福尔斯之间的路上的一家餐馆见面。 阿什莉和她的父母都开车两个小时去了餐厅。 Ashley 的平均速度比她父母的平均速度快七英里/小时。 找出阿什利和她父母的平均速度。

回答

阿什利的父母开了 55 英里/小时，阿什利开了 62 英里/小时

在阅读下一个示例时，请考虑行驶距离的关系。 前两个例子中哪一个更类似于这种情况？

示例\(\PageIndex{19}\)

两名卡车司机同时离开州际公路上的休息区。 一辆卡车向东行驶，另一辆向西行驶。 向西行驶的卡车以 70 英里/小时的速度行驶，向东行驶的卡车的平均时速为 60 英里/小时。 它们在相隔 325 英里之前要行驶多久？

回答

第 1 步。 阅读问题。 让所有的文字和想法都被理解。

画一张图来说明发生了什么。

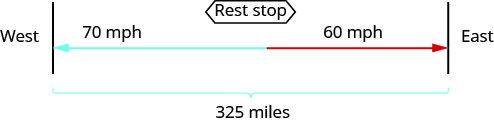
创建一个表来组织信息。

• 标注速率、时间、距离列。
• 列出两个场景。
• 写下你知道的信息。
  
  

第 2 步。 确定我们在寻找什么。

我们被要求找出卡车在相距 325 英里之前行驶的时间。

第 3 步。 说出我们要找的东西。 选择一个变量来表示该数量。

完成图表。 使用变量表达式表示每行中的该数量。
我们正在寻找时光流逝。 两辆卡车的行驶时间相同。
让我们称时间为 t。 由于它们的速度不同，它们将行驶不同的距离。

将速率乘以时间得出距离。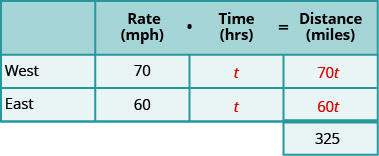

第 4 步。 翻译成方程式。

用一句话用所有重要信息重述问题。 然后，将句子翻译成方程式。
我们需要找到距离之间的关系才能写出方程。 从图中可以看出，每辆卡车的行驶距离之间有什么关系？
卡车向西行驶的距离加上卡车向东行驶的距离加起来必须为 325 英里。 所以我们这样写：

第 5 步。 使用代数技术求解方程。

\( \quad \text{Now solve this equation} \qquad\begin{align} 70t+60t &= 325 \nonumber\\ 130t &= 325 \nonumber\\ t &= 2.5 \nonumber\\ \end{align} \)

因此，卡车需要\(2.5\)几个小时才能相隔 325 英里。

第 6 步。 检查问题中的答案并确保答案合理。

\(\begin{array} {llll} \text{Truck going West} &{70\text{ mph}(2.5\text{ hours})} &= &{\space175\text{ miles}\space} \\ \text{Truck going East} &{60\text{ mph}(2.5\text{ hours})} &= &{\underline{\space150\text{ miles}\space}} \\ {} &{} &{} &{325\text{ miles}\checkmark} \\ \end{array}\)

第 7 步。 用完整的句子回答问题。
卡车需要 2.5 个小时才能相隔 325 英里。

示例\(\PageIndex{20}\)

皮埃尔和莫妮克同时离开了他们在波特兰的家。 皮埃尔在收费公路上以每小时 75 英里的速度向北行驶，而莫妮克则以每小时 68 英里的速度向南行驶。 他们相隔 429 英里需要多长时间？

回答

皮埃尔和莫妮克将在 3 小时内相隔 429 英里。

示例\(\PageIndex{21}\)

Thanh 和 Nhat 同时离开了他们在萨克拉曼多的办公室。 Thanh 在 I-5 上以每小时 72 英里的速度向北行驶。 Nhat 在 I-5 上以每小时 76 英里的速度向南行驶。 他们相距 330 英里需要多长时间？

回答

Thanh 和 Nhat 将在 2.2 小时内相隔 330 英里。

当我们使用距离速率和时间公式时，请务必确保单位匹配。 例如，如果费率以英里/小时为单位，则时间必须以小时为单位。

示例\(\PageIndex{22}\)

当 Naoko 步行去学校时，她要花 30 分钟。 如果她骑自行车，则需要 15 分钟。 她骑自行车时的速度比走路时快三英里/小时。 她的速度行走和骑自行车的速度是多少？

回答

首先，我们绘制一张代表情况的图表，以帮助我们了解正在发生的事情。

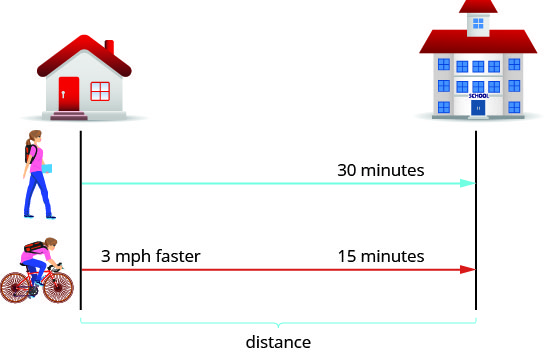
我们被要求找到她的速度行走和骑自行车。 让我们称她为步行速度 r。 由于她的骑行速度快了每小时三英里，所以我们称之为这个速度\(r+3\)。 我们在图表中写下速度。

速度以英里/小时为单位，因此我们也需要用小时表示时间，以使单位相同。 请记住，1 小时等于 60 分钟。 所以：

\[\begin{array} {l} {} \\ \text{30 minutes is } \frac{30}{60} \text{ or }\frac{1}{2}\text{ hour} \\ \text{15 minutes is } \frac{15}{60} \text{ or }\frac{1}{4}\text{ hour} \\ \nonumber \end{array}\]

我们在图表中写下时间。

接下来，我们将速率乘以时间来填充距离列。

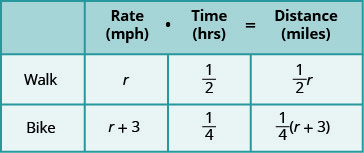
方程式将来自这样一个事实，即无论她是走路还是骑自行车，Naoko从家到学校的距离都是一样的。
所以我们说：

转换为方程。
求解这个方程。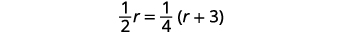
通过将方程中所有分数乘以 LCD 来清除分数。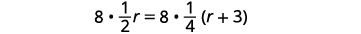
简化。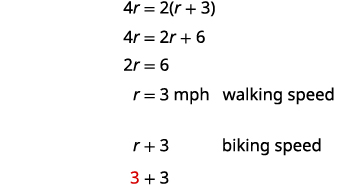
	6
让我们来看看这是否奏效。 \(\begin{array} {lll} {\text{Walk }3\text{ mph }(0.5\text{ hour})} &= &{1.5\text{ miles}} \\ {\text{Bike }6\text{ mph }(0.25\text{ hour})} &= &{1.5\text{ miles}} \\ \end{array}\)

是的，无论哪种方式，直子都要走1.5英里去学校。

Naoko 的步行速度为 3 英里/小时，她骑自行车的速度为 6 英里/小时。

示例\(\PageIndex{23}\)

Suzy 从停车场徒步上坡到瞭望塔需要 50 分钟。 她花了 30 分钟才徒步回到停车场。 她下坡的速度比上坡速度快1.2英里/小时。 查找 Suzy 的上坡和下坡速度。

回答

Suzy 的上坡速度为 1.81.8 英里/小时，下坡速度为 3 英里/小时。

示例\(\PageIndex{24}\)

Llewyn 花了 45 分钟将他的船从码头向上游开到他最喜欢的钓鱼点。 他花了 30 分钟才把船开回下游到码头。 这艘船向下游行驶的速度比向上游行驶的速度快四英里/小时。 查找船的上游和下游速度。

回答

船的上游速度为 8 英里/小时，下游速度为 12 英里/小时。

在距离、速率和时间公式中，时间代表实际经过的时间（以小时、分钟等为单位）。 如果问题将开始和结束时间作为时钟时间，则我们必须找到经过的时间才能使用公式。

示例\(\PageIndex{25}\)

克鲁兹正在训练参加铁人三项比赛。 他在 6:00 离开家，一直跑到 7:30。 然后他骑着自行车直到 9:45。 他总共行驶了 51 英里。 他骑自行车时的速度是跑步时速度的1.6倍。 查找 Cruz 的骑行和跑步速度。

回答

一张图表将帮助我们模拟这次旅行。

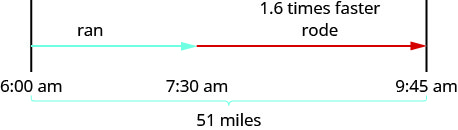
接下来，我们创建一个表来组织信息。 我们知道总距离为 51 英里。 我们正在寻找行程中每个部分的速度速度。 骑自行车时的速度是跑步速度的1.6倍。 如果我们让 r = 速率运行，则速率循环为 1.6 r。

这里的时间以时钟时间给出。 克鲁兹在早上 6:00 从家开始，早上 7:30 开始骑自行车。所以他花了 1.5 个小时跑步。 然后他从早上 7:30 到上午 9:45 骑自行车。所以他花了 2.25 个小时骑自行车。

现在，我们将费率乘以乘以。

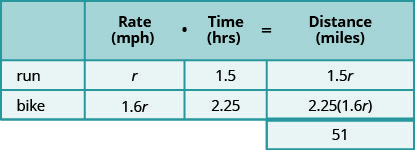
通过查看图表，我们可以看到跑步距离和长距离骑行之和为 255 英里。

转换为方程。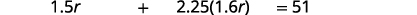
求解这个方程。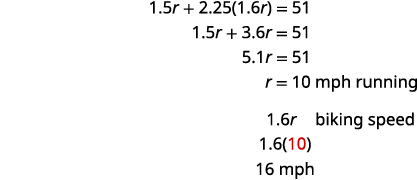
查看。 \(\begin{array} {lll} {\text{Run }10\text{ mph }(1.5\text{ hour})} &= &{15\text{ mi}} \\ {\text{Bike }16\text{ mph }(2.25\text{ hour})} &= &{\underline{36\text{ mi}}} \\ {} &{} &{} &{51\text{ mi}} \\ \end{array}\)

示例\(\PageIndex{26}\)

汉密尔顿喜欢去拉斯维加斯旅游，距离他在奥兰治县的家255英里。 在他最后一次旅行中，他在下午 2 点离开了家。他旅行的第一部分是在拥挤的城市高速公路上。 下午 4:00，交通畅通无阻，他能够以比在拥挤区域开车时快 1.75 倍的速度穿越沙漠。 他在下午 6:30 抵达拉斯维加斯。他在行程的每个环节都开车多快？

回答

汉密尔顿在城市中行驶 40 英里/小时，在沙漠中行驶 70 英里/小时。

示例\(\PageIndex{27}\)

Phuong 在 10:00 骑自行车离开了家。 他在平坦的街道上骑车直到 11:15，然后上坡直到 11:45。 他总共骑了 31 英里。 他在平坦的街道上骑行速度是他在平坦街道上速度的0.6倍。 在平坦的街道上找到他的速骑自行车。

回答

Phuong 以 12 英里/小时的速度上坡，在平坦的街道上以 20 英里/小时的速度骑行。

关键概念

• 硬币的@@ 总价值
  对于相同类型的硬币，使用型号·value=totalvaluen
  umber·value=totalvalue=totalvalue来找到许多硬币的总价值
  • 数字是硬币的数量
  • 价值是每枚硬币的价值
  • 总价值是所有硬币的总价值
• 如何解决硬币单词问题。
  1. 阅读问题。 确保所有文字和想法都被理解。
     确定所涉及的硬币类型。
     创建一个表来组织信息。
     将列标记为 “类型”、“数字”、“值”、“总值”。
     列出硬币的类型。
     写下每种硬币的价值。
     写下所有硬币的总价值。
     
  2. 确定你在找什么。
  3. 说出你要找的东西。 选择一个变量来表示该数量。
     使用变量表达式表示每种硬币的数量并将其写入表中。
     将数字乘以该值得出每种硬币的总价值。
  4. 翻译成方程式。
     用一句话用所有重要信息重述问题可能会有所帮助。 然后，将句子翻译成方程式。
     通过将所有类型硬币的总值相加来写出方程式。
  5. 使用良好的代数技巧求@@ 解方程。
  6. 检查问题中的答案并确保答案合理。
  7. 用完整的句子@@ 回答问题。
• 如何解决均匀运动应用程序
  1. 阅读问题。 确保所有文字和想法都被理解。
     画一张图来说明发生了什么。
     创建一个表来组织信息。
     标注速率、时间、距离列。
     列出两个场景。
     写下你知道的信息。
     
  2. 确定你在找什么。
  3. 说出你要找的东西。 选择一个变量来表示该数量。
     完成图表。
     使用变量表达式表示每行中的该数量。
     将速率乘以时间得出距离。
  4. 翻译成方程式。
     用一句话用所有重要信息重述问题。
     然后，将句子翻译成方程式。
  5. 使用良好的代数技巧求@@ 解方程。
  6. 检查问题中的答案并确保答案合理。
  7. 用完整的句子@@ 回答问题。