2.4E：练习

练习成就完美

求解特定变量的公式

在以下练习中，求解指定变量的给定公式。

1。 求解公$C=πd$式$d$。

回答

$d=\dfrac{C}{π}$

2。 求解公$C=πd$式$π$。

3。 求解公$V=LWH$式$L$。

回答

$L=\dfrac{V}{WH}$

4。 求解公$V=LWH$式$H$。

5。 求解公$A=\frac{1}{2}bh$式$b$。

回答

$b=\dfrac{2A}{h}$

6。 求解公$A=\frac{1}{2}bh$式$h$。

7。 求解公式

$A=\frac{1}{2}d_1d_2$对于$d_1$。

回答

$d_1=\dfrac{2A}{d_2}$

8。 求解公式

$A=\frac{1}{2}d_1d_2$为了$d_2.$

9。 求解公式

$A=\frac{1}{2}h(b_1+b_2)$对于$b_1$。

回答

$b_1=\dfrac{2A}{h}−b_2$

10。 求解公式

$A=\frac{1}{2}h(b_1+b_2)$对于$b_2$。

11。 求解公式

$h=54t+\frac{1}{2}at^2$对于$a$。

回答

$a=\dfrac{2h−108t}{t^2}$

12。 求解公式

$h=48t+\frac{1}{2}at^2$对于$a$。

13。 $180=a+b+c$求解$a$。

回答

$a=180−b−c$

14。 解决$180=a+b+c$ for$c$。

15。 求解公式

$A=\frac{1}{2}pI+B$对于$p$。

回答

$p=\dfrac{2A−2B}{I}$

16。 求解公式

$A=\frac{1}{2}pI+B$对于$I$。

17。 求解公式

$P=2L+2W$对于$L$。

回答

$L=\dfrac{P−2W}{2}$

18。 求解公式

$P=2L+2W$对于$W$。

在以下练习中，求解公式$y$。

19。 求解公式

$8x+y=15$对于$y$。

回答

$y=15−8x$

20。 求解公式

$9x+y=13$对于$y$。

21。 求解公式

$−4x+y=−6$对于$y$。

回答

$y=−6+4x$

22。 求解公式

$−5x+y=−1$对于$y$。

23。 求解公式

$x−y=−4$对于$y$。

回答

$y=4+x$

24。 求解公式

$x−y=−3$对于$y$。

25。 求解公式

$4x+3y=7$对于$y$。

回答

$y=\frac{7−4x}{3}$

26。 求解公式

$3x+2y=11$对于$y$。

27。 求解公式

$2x+3y=12$对于$y$。

回答

$y=\frac{12−2x}{3}$

28。 求解公式

$5x+2y=10$对于$y$。

29。 求解公式

$3x−2y=18$对于$y$。

回答

$y=\frac{18−3x}{−2}$

30。 求解公式

$4x−3y=12$对于$y$。

使用公式求解几何应用程序

在以下练习中，使用几何公式求解。

31。 三角旗的面积为 0.75 平方英尺，高 1.5 英尺。 它的基础是什么？

回答

1 英尺

32。 三角窗的面积为 24 平方英尺，高度为 6 英尺。 它的基础是什么？

33。 面积为 207 平方英寸、高 18 英寸的三角形的底部是什么？

回答

23 英寸

34。 面积为 893 平方英寸、底部为 38 英寸的三角形的高度是多少？

35。 直角三角形的两个较小角度的度量相等。 找到所有三个角度的测量值。

回答

$45°,\; 45°,\; 90°$

36。 直角三角形最小角度的度量小于下一个较大角度的度量。$20°$ 找到所有三个角度的测量值。

37。 三角形中的角度使得一个角度是最小角度的两倍，而第三个角度是最小角度的三倍。 找到所有三个角度的测量值。

回答

$30°,\; 60°,\; 90°$

38。 三角形中的角度使得一个角度$20$比最小角度大，而第三个角度是最小角度的三倍。 找到所有三个角度的测量值。

在以下练习中，使用毕达哥拉斯定理找出斜边的长度。

39。

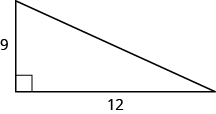
回答

$15$

40。

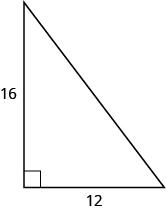
41。

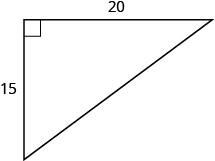
回答

$25$

42。

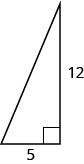
在以下练习中，使用毕达哥拉斯定理找出未知腿的长度。 如有必要，四舍五入到最接近的十分之一。

43。

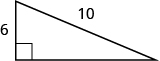
回答

$8$

44。

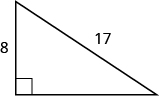
45。

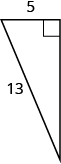
回答

$12$

46。

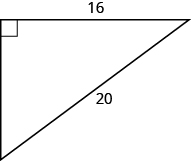
47。

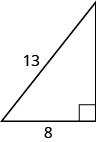
回答

$10.2$

48。

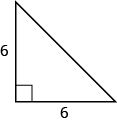
49。

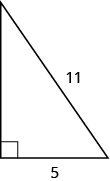
回答

$9.8$

50。

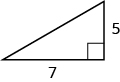
在以下练习中，使用几何公式求解。

51。 矩形的宽度比长度小七米。 周长为$58$米。 找出长度和宽度。

回答

$18$米、$11$米

52。 矩形的长度比宽度多八英尺。 周长是$60$英尺。 找出长度和宽度。

53。 矩形的宽度比长度小$0.7$米。 矩形的周长为$52.6$米。 找到矩形的尺寸。

回答

$13.5$嗯，$12.8$m

54。 矩形的长度比宽度小$1.1$米。 矩形的周长为$49.4$米。 找到矩形的尺寸。

55。 矩形$150$英尺的周长。 矩形的长度是宽度的两倍。 找出矩形的长度和宽度。

回答

$25$英尺，$50$英尺

56。 矩形的长度是宽度的三倍。 矩形的周长为$72$英尺。 找出矩形的长度和宽度。

57。 矩形的长度小于宽度的两倍的三米。 矩形的周长为$36$米。 找到矩形的尺寸。

回答

$7$嗯，$11$m

58。 矩形的长度比宽度的两倍多五英寸。 周长是$34$ inches. Find the length and width.

59。 三角形的周长为$39$英尺。 三角形的一边比第二边长一英尺。 第三边比第二边长两英尺。 找出每边的长度。

回答

$12$英尺、$13$英尺、$14$英尺

60。 三角形的周长为$35$英尺。 三角形的一边比第二边长五英尺。 第三边比第二边长三英尺。 找出每边的长度。

61。 三角形的一边是最小边的两倍。 第三边比最短边多五英尺。 周长是$17$英尺。 找出所有三个边的长度。

回答

$3$英尺、$6$英尺、$8$英尺

62。 三角形的一边是最小边的三倍。 第三边比最短边多三英尺。 周长是$13$英尺。 找出所有三个边的长度。

63。 矩形场的周长为$560$码。 长度比宽度多$40$码。 找出字段的长度和宽度。

回答

$120$是的，$160$是的

64。 矩形中庭的周长为$160$英尺。 长度比宽度多$16$英尺。 找出中庭的长度和宽度。

65。 矩形停车场的周长为$250$英尺。 长度是五英尺，是宽度的两倍多。 找到停车场的长度和宽度。

回答

$40$英尺，$85$英尺

66。 矩形地毯的周长$240$为英寸。 长度是$12$英寸是宽度的两倍以上。 找出地毯的长度和宽度。

在以下练习中，求解。 如有必要，将答案近似至最接近的十分之一。

67。 如图所示，将在$13$-f$12$ oot 杆的顶部安装一串灯，用于节日展示。 灯串的末端应该停在离灯杆底部多远的地方？

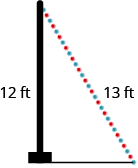
回答

$5$英尺

68。 如图所示，帕姆想在车库门对角线上放一面横幅，祝贺儿子大学毕业。 车库门高$12$英尺，宽$16$英尺. 横幅需要多长时间才能装上车库门？

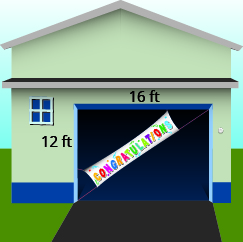
69。 Chi 计划在她的花园里铺设一条铺路石的对角线，如图所示。 花园是一个有侧$10$脚的广场。 路径的长度是多少？

回答

$14.1$英尺

70。 布莱恩借了一个$20$伸展梯子，用来粉刷房子。 如果他如图所示将梯子的底部设置在离房子六英尺远的地方，梯子的顶部会到达多远？

日常数学

71。 转换温度在希腊巡回演出时，塔季扬娜发现温度为$40°$摄氏度。 在公式$F$中求解 for$C=\frac{5}{9}(F−32)$ 以求出华氏温度。

回答

$104°$F

72。 转换温度 Yon 正在访问美国，他发现西雅图有一天温度为$50°$华氏度。 在公式$C$中求解 for$F=\frac{9}{5}C+32$ 以求出摄氏温度

73。 克里斯塔想在她的三角花坛周围放一道围栏。 花坛的两侧是六英尺、八英尺和$10$英尺。 她需要多少英尺的围栏才能封住花坛？

回答

$24$英尺

74。 Jose 刚刚从后院移走了儿童玩具套装，以便为矩形花园腾出空间。 他想在花园里筑一道围栏，把狗拒之门外。 他的车库里有一卷四$50$英尺长的围栏，他打算使用。 为了适应后院，花园的宽度必须为$10$英尺。 他能站到另一边多久？

写作练习

75。 如果你需要在厨房地板上铺瓷砖，你需要知道厨房的周长或面积吗？ 解释你的理由。

回答

答案会有所不同。

76。 如果你需要在后院周围设置围栏，你需要知道后院的周长或面积吗？ 解释你的理由。

77。 看下面的两个数字。

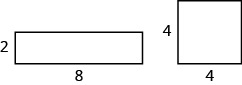
a. 哪个数字看起来面积更大？ 哪个看起来它的周长更大？

b. 现在计算每个图形的面积和周长。 哪个面积更大？ 哪个的周长更大？

c. (b) 部分的结果与你在 (a) 部分中的回答相同吗？ 这让你感到惊讶吗？

回答

a. 答案视情况而定。b. 区域相同。 $2×8$矩形的周长比$4×4$正方形大。

c. 答案视情况而定。

78。 写一个与你的生活经历相关的几何词问题，然后解决这个问题并解释你的所有步骤。

自检

a. 完成练习后，使用此清单评估您对本节目标的掌握程度。

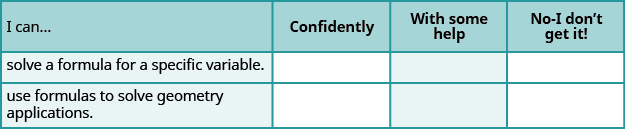
b. 关于你对本部分的掌握程度，这份清单告诉了你什么？ 你会采取哪些措施来改进？