2.4:求解特定变量的公式
- Page ID
- 204194
在本节结束时,您将能够:
- 求解特定变量的公式
- 使用公式求解几何应用程序
在开始之前,请参加这个准备测验。
求解特定变量的公式
在数学研究中,我们可能都使用过一些几何公式。 公式用于许多领域,识别公式并能够轻松操作它们非常重要。
求解特定变量的公式通常很有帮助。 如果你需要在电子表格中输入一个公式,那么必须先为一个特定的变量求解这个公式并不罕见。 我们将该变量隔离在等号的一侧,系数为 1,所有其他变量和常量位于等号的另一边。
对于另一个变量,通常也需要求解几何公式。 给定底部半径和高度时,该公式\(V=\frac{1}{3}πr^2h\)用于计算右圆锥的体积。 在下一个示例中,我们将求解这个高度公式。
求解 h\(V=\frac{1}{3}πr^2h\) 的公式。
- 回答
-
写下公式。 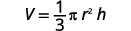
移除右边的分数。 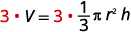
简化。 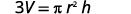
将两边除以\(πr^2\)。 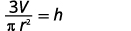
现在,当我们知道底部的体积和半径时,我们可以使用这个公式来找出右圆锥的高度,方法是使用这个公式\(h=\frac{3V}{πr^2}\)。
使用公式\(A=\frac{1}{2}bh\)求解 b。
- 回答
-
\(b=\frac{2A}{h}\)
使用公式\(A=\frac{1}{2}bh\)求解 h。
- 回答
-
\(h=\frac{2A}{b}\)
在科学领域,我们经常需要将温度从华氏度改为摄氏度,反之亦然。 如果您在国外旅行,则可能需要将摄氏温度更改为更熟悉的华氏温度。
求解 F\(C=\frac{5}{9}(F−32)\) 的公式。
- 回答
-
写下公式。 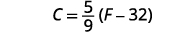
移除右边的分数。 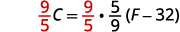
简化。 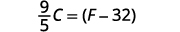
在两边加上 32。 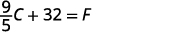
现在,当我们知道摄氏温度时,我们可以使用该公式\(F=\frac{9}{5}C+32\)来计算华氏温度。
求解 C\(F=\frac{9}{5}C+32\) 的公式。
- 回答
-
\(C=\frac{5}{9}(F−32)\)
求解 b\(A=\frac{1}{2}h(b+B)\) 的公式。
- 回答
-
\(b=\frac{2A−Bh}{h}\)
下一个示例使用右圆柱表面积的公式。
求解公\(S=2πr^2+2πrh\)式\(h\)。
- 回答
-
写下公式。 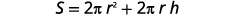
通过\(2πr^2\)从两边减去来分离该\(h\)项。 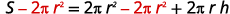
简化。 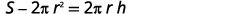
\(h\)通过将两边除以来求解\(2πr.\) 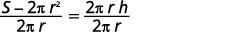
简化。 
求解公\(A=P+Prt\)式\(t\)。
- 回答
-
\(t=\frac{A−P}{Pr}\)
求解公\(A=P+Prt\)式\(r\)。
- 回答
-
\(r=\frac{A−P}{Pt}\)
有时我们可能会得到一个方程,这个方程已经求\(y\)解了,需要求解\(x\),反之亦然。 在以下示例中,我们得到了一个两\(x\)边都相同的方程,我们将对其求解\(y\)。\(y\)
求解公\(8x+7y=15\)式\(y\)。
- 回答
-
我们将在方程的一\(y\)侧进行隔离。 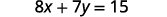
\(6x\)从两边减去以将术语与之隔离开来\(y\)。 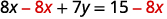
简化。 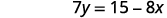
将两边除\(7\)以得出系数为\(y\)一。 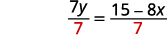
简化。 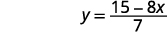
求解公\(4x+7y=9\)式\(y\)。
- 回答
-
\(y=\frac{9−4x}{7}\)
求解公\(5x+8y=1\)式\(y\)。
- 回答
-
\(y=\frac{1−5x}{8}\)
使用公式求解几何应用程序
在这个目标中,我们将使用一些常见的几何公式。 我们将调整我们的问题解决策略,以便我们可以解决几何应用程序。 几何公式将命名变量并给出要解的方程。
此外,由于这些应用程序都将涉及某种形状,因此大多数人发现绘制图形并用给定信息对其进行标记会很有帮助。 我们将在几何应用问题解决策略的第一步中包括这一点。
- 阅读问题并确保所有文字和想法都被理解。
- 确定你在找什么。
- 通过选择一个变量来表示我们要找的东西来@@ 命名它。 画出图形并用给定的信息贴上标签。
- 通过编写适合情况的公式或模型将其@@ 转换为方程。 在给定的信息中替换。
- 使用良好的代数技巧求@@ 解方程。
- 检查问题中的答案并确保答案合理。
- 用完整的句子@@ 回答问题。
当我们求解几何应用程序时,我们经常必须使用图形的某些属性。 我们将根据需要审查这些房产。
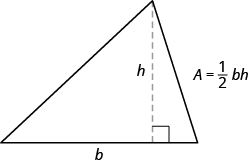
下一个示例涉及三角形的面积。 三角形的面积是基数乘以高度的一半。 我们可以把它写成\(A=\frac{1}{2}bh\),其中\(b\) = 基数的长度,\(h\)= 高度。
三角画的\(126\)面积为平方英寸。 底座是\(18\)英寸。 身高是多少?
- 回答
-
第 1 步。 阅读问题。 第 2 步。 确定你在找什么。 三角形的高度 第 3 步。 姓名。 选择一个变量来表示它。 让\(h=\)高度。 画出图形并用给定的信息贴上标签。 面积 = 126 平方英寸 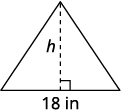
第 4 步。 翻译。 写出相应的公式。 \(A=\frac{1}{2}bh\) 在给定的信息中替换。 \(126=\frac{1}{2}·18·h\) 第 5 步。 求解方程。 \(126=9h\) 将两边除以 9。 \(14=h\) 第 6 步。 查看。 \(\begin{align*} A &= \frac{1}{2}bh \\126 & \stackrel{?}{=} 12·18·14 \\ 126 &=126✓ \end{align*}\)
第 7 步。 回答问题。 三角形的高度为\(14\)英寸。
三角形教堂窗户的\(90\)面积为平方米。 窗户的底部是\(15\)米。 窗户的高度是多少?
- 回答
-
窗户的高度是\(12\)米。
三角形帐篷门的面积为\(15\)平方英尺。 高度为五英尺。 底座的长度是多少?
- 回答
-
底座的长度为\(6\)英尺。
在下一个示例中,我们将使用直角三角形。 为了求解每个角度的测量,我们需要使用两个三角形属性。 在任何三角形中,角度的测量值之和为\(180°\)。 我们可以把它写成一个公式:\(m∠A+m∠B+m∠C=180\). 另外,由于三角形是直角三角形,因此我们记得直角三角形只有一个\(90°\)角度。
在这里,我们必须用另一个角度来定义一个角度。 我们将等待绘制图形,直到我们为要寻找的所有角度写出表达式为止。
直角三角形的一个角度的测量值比最小角度的度量高 40 度。 找出所有三个角度的测量值。
- 回答
-
第 1 步。 阅读问题。 第 2 步。 确定你在找什么。 所有三个角度的测量 第 3 步。 姓名。 选择一个变量来表示它。 \(\begin{align*} \text{Let }a \; & = \; \mathrm{1^{st} \; angle.} \\ a+40 &= \mathrm{2^{nd} \; angle} \\90 &= \mathrm{3^{rd} \; angle \; (the \; right \; angle)} \end{align*}\) 画出图形并用给定的信息贴上标签。 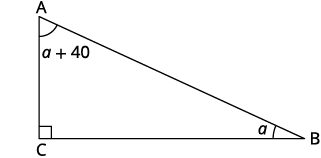
第 4 步。 翻译。 写出相应的公式。 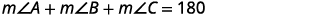
代入配方。 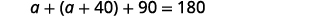.jpg)
第 5 步。 求解方程。 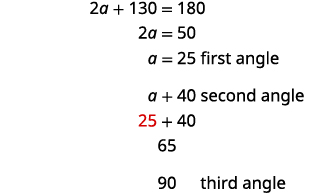
第 6 步。 查看。 \( \begin{align*} 25+65+90 & \stackrel{?}{=} 180\\ 180 &= 180✓ \end{align*}\) 第 7 步。 回答问题。 三个角度测量\(25°,\;65°\),和\(90°\)。
直角三角形的一个角度的度量比最小角度的度量多 50。 找出所有三个角度的测量值。
- 回答
-
角度的测量值为\(20°, \;70°\)、和\(90°\)。
直角三角形的一个角度的度量大\(30\)于最小角度的度量。 找出所有三个角度的测量值。
- 回答
-
角度的测量值为\(30°,\; 60°\)、和\(90°\)。
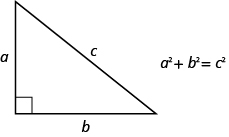
下一个示例使用了另一个重要的几何公式。 毕达哥拉斯定理讲述了直角三角形的三条边的长度是如何相互关联的。 在每个练习中写下公式并在写作时大声说出来,可能有助于你记住毕达哥拉斯定理。
在任何直角三角形中,a 和 b 是腿的长度,c 是斜边的长度,两条腿长度的平方和等于斜边长度的平方。
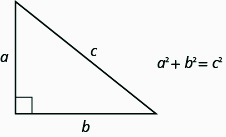
我们将在下一个示例中使用毕达哥拉斯定理。
使用毕达哥拉斯定理找出另一条腿的长度
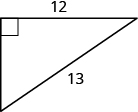
- 回答
-
第 1 步。 阅读问题。 第 2 步。 确定你在找什么。 三角形腿的长度 第 3 步。 姓名。 选择一个变量来表示它。 让\(a\) = 三角形的腿。 在 a 面贴标签 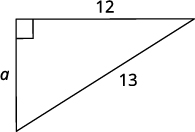
第 4 步。 翻译。 写出相应的公式。 替代。 \(\begin{align*}a^2+b^2 &=c ^2 \\ a^2+12^2 &=13^2 \end{align*}\) 第 5 步。 求解方程。 分离变量项。 使用平方根的定义。 简化。 \(\begin{align*} a^2+144 &= 169 \\ a^2 &= 25 \\ a &= \sqrt{25} \\ a&=5 \end{align*}\) 第 6 步。 查看。 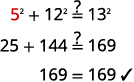
第 7 步。 回答问题。 腿的长度是\(5\)。
使用毕达哥拉斯定理在图中找出腿的长度。
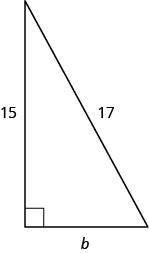
- 回答
-
腿的长度是\(8\)。
使用毕达哥拉斯定理在图中找出腿的长度。
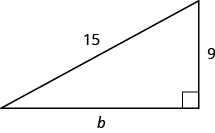
- 回答
-
腿的长度是\(12\)。
下一个示例是关于矩形的周长。 由于周长只是矩形周围的距离,因此我们可以找到其四边长度的总和——两个长度和两个宽度的总和。 我们可以把 is 写成长度\(P=2L+2W\)在哪里\(L\),宽\(W\)度在哪里。 为了解决这个例子,我们需要根据宽度来定义长度。
矩形的长度是宽度的两倍以上的六厘米。 周长为\(96\)厘米。 找出长度和宽度。
- 回答
-
第 1 步。 阅读问题。 第 2 步。 确定我们在寻找什么。 长度和宽度 第 3 步。 姓名。 选择一个变量来表示宽度。 长度为六倍是宽度的两倍。 让\(w=\)宽度。 \(2w+6=\)长度
\(P=96\)厘米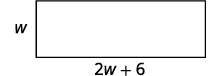
第 4 步。 翻译。 写出相应的公式。 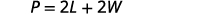
在给定的信息中替换。 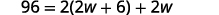
第 5 步。 求解方程。 
第 6 步。 查看。
\(\begin{align*} P &=2L+2W \\ 96 & \stackrel{?}{=}2·34+2·14 \\ 96 &=96✓ \end{align*}\)
第 7 步。 回答问题。 长度为\(34\)厘米,宽度为\(14\)厘米
矩形的长度是宽度的七倍多。 周长为\(110\)英寸。 找出长度和宽度。
- 回答
-
长度为\(16\)英寸,宽度为\(39\)英寸。
矩形的宽度小于长度的两倍八码。 周长是\(86\)码。 找出长度和宽度。
- 回答
-
长度是\(17\)码,宽度是\(26\)码。
下一个示例是关于三角形的周长。 由于周长只是三角形周围的距离,因此我们可以找到其三边长度的总和。 我们可以将其写成\(P=a+b+c\)、位置\(a\)\(b\)、和\(c\)边的长度。
三角形的一边比第一边多三英寸。 第三面比第一面多两英寸。 周长为\(29\)英寸。 找出三角形三边的长度。
- 回答
-
第 1 步。 阅读问题。 第 2 步。 确定我们在寻找什么。 三角形三边的长度 第 3 步。 姓名。 选择一个变量来表示第一边的长度。 \( \begin{align*} \mathrm{Let \;}x \;& \mathrm{= \; length \; of \;1^{st} \;side.} \\ x+3 \; &= \; \mathrm{length \; of \; 2^{nd} \; side} \\ 2x+2 \; &= \; \mathrm{length \; of \;3^{rd} \; side} \end{align*}\)
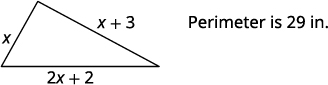
第 4 步。 翻译。 写出相应的公式。 在给定的信息中替换。 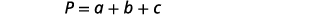
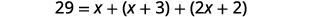
第 5 步。 求解方程。 
第 6 步。 查看。
\(\begin{align*} 29 & \stackrel{?}{=}6+9+14 \\ 29 &= 29✓ \end{align*}\)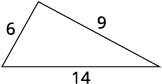
第 7 步。 回答问题。 三角形边的长度为\(6\)\(9\)、和\(14\)英寸。
三角形的一边比第一边多七英寸。 第三面比第一边小四英寸。 周长为\(28\)英寸。 找出三角形三边的长度。
- 回答
-
三角形边的长度\(12\)为\(11\)和英寸。\(5\)
三角形的一边比第一边小三英尺。 第三边小五英尺,比第一边少两倍。 周长是\(20\)英尺。 找出三角形三边的长度。
- 回答
-
三角形边的长度为\(4\)\(7\)和\(9\)英尺。
矩形足球场的周长为\(360\)英尺。 长度比宽度多\(40\)英尺。 找出长度和宽度。
- 回答
-
第 1 步。 阅读问题。 第 2 步。 确定我们在寻找什么。 足球场的长度和宽度 第 3 步。 姓名。 选择一个变量来表示它。 长度比宽度多 40 英尺。 画出图形并用给定的信息贴上标签。 假设 w = 宽度。 \(w+40=\)长度 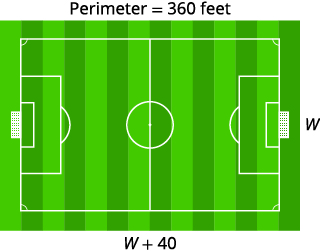
第 4 步。 翻译。 写出相应的公式并替代。 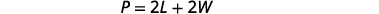
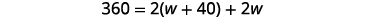
第 5 步。 求解方程。 第 6 步。 查看。 \( \begin{align*} P &=2L+2W \\ 360 & \stackrel{?}{=} 2(110)+2(70) \\360 &=360✓ \end{align*}\) 
第 7 步。 回答问题。 足球场的长度是\(110\)英尺,宽度是\(70\)英尺。
矩形游泳池的周长为\(200\)英尺. 长度比宽度多\(40\)英尺。 找出长度和宽度。
- 回答
-
游泳池的长度为\(70\)英尺,宽度为\(30\)英尺.
矩形花园的长度比宽度多几\(30\)码。 周长是\(300\)码。 找出长度和宽度。
- 回答
-
花园的长度是\(90\)码,宽度是\(60\)码.
这些几何特性的应用可以在许多日常情况下找到,如下一个示例所示。
开尔文正在建造一个凉亭,他想通过在对角线上放置一块 10 英寸的木头来支撑每个角落,如图所示。
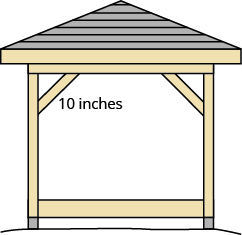
如果想与角落的距离相等,他应该把木头固定在离角落多远? 近似于最接近的十分之一英寸。
- 回答
-
第 1 步。 阅读问题。 第 2 步。 确定我们在寻找什么。 支架应安装到角落的距离 第 3 步。 姓名。 选择一个变量来表示它。 画出图形并用给定的信息贴上标签。 让\(x=\)距离角落保持距离。 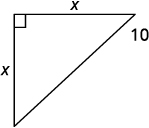
第 4 步。 翻译。 写出相应的公式并替代。 \(a^2+b^2=c^2\)\(x^2+x^2=10^2\) 第 5 步。 求解方程。 隔离变量。
使用平方根的定义。简化。 近似到最接近的十分之一。
\( \begin{align*} 2x^2 &= 100 \\ \\ x^2 &=50 \\ \\ x &= \sqrt{50} \\ \\ x &≈7.1 \end{align*}\)
第 6 步。 查看。 \( \begin{align*} a^2+b^2 &= c^2 \\ (7.1)^2+(7.1)^2 &≈10^2 \; \;\;\;\; \text{Yes.} \end{align*}\)
第 7 步。 回答问题。 开尔文应该将每块木头固定在距离角落大约 7.1 英寸的地方。
如图所示,约翰把一\(13\)英尺高的梯子的底部放在离他家墙壁五英尺远的地方。 梯子能到达墙上多远?

- 回答
-
梯子伸到了\(12\)英尺。
如图所示,\(17\)兰迪想在帆船的\(15\)脚桅顶部安装一根英尺长的灯串。 他应该把灯串的末端固定在离桅杆底部多远的地方?
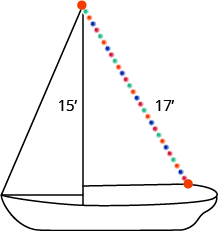
- 回答
-
他应该把灯安装在距离桅杆底部的\(8\)脚上。
访问此在线资源,获取更多指导和练习如何求解文字方程中的变量。
- 求解文字方程
关键概念
- 如何解决几何应用程序
- 阅读问题并确保所有文字和想法都被理解。
- 确定你在找什么。
- 通过选择一个变量来表示你要找的东西来@@ 命名它。 画出图形并用给定的信息贴上标签。
- 通过编写适合情况的公式或模型将其@@ 转换为方程。 在给定的信息中替换。
- 使用良好的代数技巧求@@ 解方程。
- 检查问题中的答案并确保答案合理。
- 用完整的句子@@ 回答问题。
- 毕达哥拉斯定理
- 在任何直角三角形中,a 和 b 是腿的长度,c 是斜边的长度,两条腿长度的平方和等于斜边长度的平方。