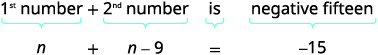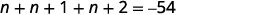2.3: 使用问题解决策略
- Page ID
- 204264
在本节结束时,您将能够:
- 使用问题解决策略来解决单词问题
- 解决数字词问题
- 求解应用程序百分比
- 解决单息申请
在开始之前,请参加这个准备测验。
你过去有没有在单词问题上遇到过负面经历? 当我们觉得自己无法控制并继续重复消极想法时,我们就会为成功设置障碍。 意识到你在单词问题上的负面经历已经过去了。 要向前迈进,你需要平息恐惧并改变负面情绪。
从全新的角度开始,开始思考积极的想法。 重复以下一些陈述可能有助于使你的想法变得积极。 思考积极的想法是迈向成功的第一步。
- 我想我可以! 我想我可以!
- 虽然过去单词问题很难,但我想我现在可以尝试一下。
- 我现在准备得更好了——我想我会开始理解单词问题了。
- 我之所以能够求解方程式,是因为我练习了很多问题,在需要的时候我得到了帮助,我可以尝试一下单词问题。
- 这可能需要时间,但我可以开始解决单词问题。
- 你现在已经做好了充分的准备,为成功做好了准备。 如果你掌控一切,相信自己能成功,你就能掌握单词问题。
对单词问题使用问题解决策略
现在我们可以求解方程了,我们已经准备好将我们的新技能应用于单词问题了。 我们将制定一种可以用来成功解决任何单词问题的策略。
当地滑雪胜地的正常年降雪量为12英寸,是上季降雪量的两倍。 正常的年降雪量为 62 英寸。 上个季节滑雪胜地的降雪量是多少?
解决方案:
| 第 1 步。 阅读问题。 | |
| 第 2 步。 确定你在找什么。 | 上个季节的降雪量是多少? |
| 第 3 步。 命名我们要查找的内容,然后选择一个变量来表示它。 | 让\(s=\)上个季节降雪吧。 |
| 第 4 步。 翻译。 用一句话用所有重要信息重述问题。 |  |
| 翻译成方程式。 |  |
| 第 5 步。 求解方程。 | 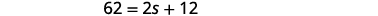 |
| 每边减去 12。 | 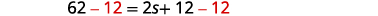 |
| 简化。 |  |
| 将每边除以二。 |  |
| 简化。 |  |
| 第 6 步。 检查:首先,我们的答案合理吗? 是的,有 25 英寸的积雪似乎还可以。 问题是,正常降雪量是上个季节的两倍多十二英寸。 两次 25 是 50,比那个多 12,也就是 62。 | |
| 第 7 步。 回答问题。 | 上个季节的降雪量为25英寸。 |
吉列尔莫在书店买了教科书和笔记本。 教科书数量为三本,是笔记本数量的两倍多。 他买了七本教科书。 他买了多少本笔记本电脑?
- 回答
-
他买了两本笔记本
Gerry 本周制作了数独谜题和填字游戏。 他完成的数独谜题数量是填字游戏数量的两倍多八个。 他完成了 22 个数独谜题。 他做了多少填字游戏?
- 回答
-
他做了七个填字游戏
我们总结了解决问题的有效策略。
- 阅读问题。 确保所有文字和想法都被理解。
- 确定你在找什么。
- 说出你要找的东西。 选择一个变量来表示该数量。
- 翻译成方程式。 用一句话用所有重要信息重述问题可能会有所帮助。 然后,将英语句子翻译成代数方程。
- 使用正确的代数技术求@@ 解方程。
- 检查问题中的答案以确保答案合理。
- 用完整的句子@@ 回答问题。
解决数字词问题
现在,我们将把问题解决策略应用于 “数字词问题”。 数字词问题提供了有关一个或多个数字的一些线索,我们使用这些线索来写一个方程式。 数字词问题为使用问题解决策略提供了很好的练习。
七乘以一个数字和八的总和等于三十六。 找到号码。
解决方案:
| 第 1 步。 阅读问题。 | |
|---|---|
| 第 2 步。 确定你在找什么。 | 这个数字 |
|
第 3 步。 说出你要找的东西然后 选择一个变量来表示它。 |
让\(n=\)数字来。 |
|
第 4 步。 翻译: 用一句话重述问题。 翻译成方程式。 |
|
|
第 5 步。 求解方程。 从每边减去八个然后简化。 将每边除以七然后简化。 |
|
|
第 6 步。 查看。 七乘以四加八的总和等于 36 吗? \[\begin{align*} 7·4+8 & \stackrel{?}{=}36 \\ 28+8 & \stackrel{?}{=}36 \\ 36 & =36✓ \end{align*}\] |
|
| 第 7 步。 回答问题。 | 这个数字是 4。 |
你有没有注意到我们在求解这个方程式时遗漏了一些步骤? 如果您还没有准备好省略这些步骤,请根据需要写下任意数量的步骤。
四乘以一个数字和二的总和等于十四。 找到号码。
- 回答
-
\(3\)
三乘以一个数字和七的总和等于二十五。 找到号码。
- 回答
-
\(6\)
一些数字词问题要求我们找到两个或多个数字。 用不同的变量命名它们可能很诱人,但是到目前为止,我们只用一个变量求解了方程。 为了避免使用多个变量,我们将根据同一个变量定义数字。 一定要仔细阅读问题,以了解所有数字之间的关系。
两个数字的总和为负十五。 一个数字比另一个数字少九个。 找到数字。
解决方案:
| 第 1 步。 阅读问题。 | |
| 第 2 步。 确定你在找什么。 | 两个数字 |
| 第 3 步。 通过选择一个代表第一个数字的变量来命名你要查找的内容。 “一个数字比另一个数字少九个。” | 让我们\(n=1^{\text{st}}\)编号。 \(n−9=2^{\text{nd}}\)数字 |
| 第 4 步。 翻译。 写成一句话。 翻译成方程式。 | 两个数字的总和为负十五。
|
|
第 5 步。 求解方程。 将相似的术语组合在一起。 每边加九个然后简化。 简化。 |
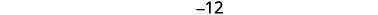 |
| 第 6 步。 查看。 比\(−12\)九少\(−3\)吗? \[\begin{align*}−3−9 & \stackrel{?}{=}−12 \\ −12 & =−12✓ \end{align*}\]是他们的总和吗\(−15?\)\[\begin{align*} −3+(−12) & \stackrel{?}{=}−15 \\ −15 & =−15✓ \end{align*}\] | |
| 第 7 步。 回答问题。 | 数字是\(−3\)和\(−12\)。 |
两个数字的总和为负二十三。 一个数字比另一个数字少七个。 找到数字。
- 回答
-
\(−15,−8\)
两个数字的总和为负十八。 一个数字比另一个多四十。 找到数字。
- 回答
-
\(−29,11\)
一些数字问题涉及连续的整数。 连续整数是紧随其后的整数。 连续整数的示例有:
\[\begin{array}{rrrr} 1, & 2, & 3, & 4 \\ −10, & −9, & −8, & −7\\ 150, & 151, & 152, & 153 \end{array}\nonumber\]
请注意,每个数字都比其前面的数字多一个。 因此,如果我们将第一个整数定义\(n,\)为下一个连续整数为\(n+1\)。 后面的那个比\(n+1\)那个多一个\(n+1+1\),就是这样\(n+2\)。
\[\begin{array}{ll} n & 1^{\text{st}} \text{integer} \\ n+1 \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; & 2^{\text{nd}}\text{consecutive integer} \\ n+2 & 3^{\text{rd}}\text{consecutive integer} \;\;\;\;\;\;\;\; \text{etc.} \end{array}\nonumber\]
在下一个示例中,我们将使用这个表示法来表示连续的整数。
找出总和为的三个连续整数\(−54\)。
解决方案:
| 第 1 步。 阅读问题。 | |
| 第 2 步。 确定你在找什么。 | 三个连续的整数 |
| 第 3 步。 分别命名三个数字 | 让\(n=1^{\text{st}} \text{integer}\)。 \(n+1=2^{\text{nd}} \text{consecutive integer}\)\(n+2=3^{\text{rd}} \text{consecutive integer}\) |
| 第 4 步。 翻译。 重述为一句话。 翻译成方程式。 | 三个整数之和为\(−54\)。
|
| 第 5 步。 求解方程。 将相似的术语组合在一起。 每边减去三个。 将每边除以三。 | 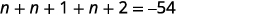 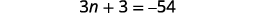 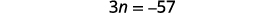 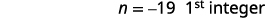
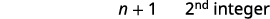 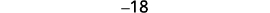 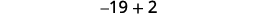 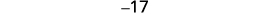 |
| 第 6 步。 查看。 \(\begin{align*} −19+(−18)+(−17) & =−54 \\ −54 & =−54✓ \end{align*}\) | |
| 第 7 步。 回答问题。 | 三个连续的整数是 −17、−18 和 −19。 |
找出总和为的三个连续整数\(−96\)。
- 回答
-
\(−33,−32,−31\)
找出总和为的三个连续整数\(−36\)。
- 回答
-
\(−13,−12,−11\)
现在我们已经处理了连续的整数,我们将扩展工作范围,将连续的偶数整数和连续的奇数整数包括在内。 连续的偶数整数是紧接着的偶数整数。 连续偶数整数的示例有:
\[24, 26, 28\nonumber\]
\[−12,−10,−8\nonumber\]
请注意,每个整数都比其前面的数字多两个。 如果我们调用第一个\(n,\),那么下一个就是\(n+2\)。 之后的那个是\(n+2+2\)或\(n+4\)。
\[\begin{array}{ll} n & 1^{\text{st}} \text{integer} \\ n+1 \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; & 2^{\text{nd}}\text{consecutive integer} \\ n+2 & 3^{\text{rd}}\text{consecutive integer} \;\;\;\;\;\;\;\; \text{etc.} \end{array}\nonumber\]
连续的奇数整数是紧随其后的奇数整数。 以连续的奇数整数 63、65 和 67 为例。
\[63, 65, 67\nonumber\]
\[n,n+2,n+4\nonumber\]
\[\begin{array}{ll} n & 1^{\text{st}} \text{integer} \\ n+1 \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; & 2^{\text{nd}}\text{consecutive integer} \\ n+2 & 3^{\text{rd}}\text{consecutive integer} \;\;\;\;\;\;\;\; \text{etc.} \end{array}\nonumber\]
必须将两个(一个偶数)相加才能得到下一个奇数看起来很奇怪吗? 当我们将 2 与 3 相加时,我们得到的是奇数还是偶数? 到 11? 到 47?
无论问题是要求连续的偶数还是奇数,你都不必做任何不同的事情。 模式还是一样的——要得到下一个奇数或下一个偶数整数,请将两个相加。
找出三个连续的偶数整数,其总和为\(120\)。
解决方案:
| 第 1 步。 阅读问题。 | |
| 第 2 步。 确定你在找什么。 | 三个连续的偶数整数 |
| 第 3 步。 分别命名三个数字 |
让\(n = 1^{\text{st}} \text{consecutive even integer}\)。 \(n + 2 = 2^{\text{nd}} \text{consecutive even integer}\)。 \(n + 4 = 3^{\text{rd}} \text{consecutive even integer}\)。 |
| 第 4 步。 翻译。
重述为一句话。 翻译成方程式。 |
三个偶数整数之和为 120 \(n + n + 2 + n + 4 = 120\) |
| 第 5 步。 求解方程。
将相似的术语组合在一起。 每边减去三个。 将每边除以三。 |
\(n + n + 2 + n + 4 = 120\) \(\begin{aligned} &{3n+6=120} \\ &{3n=114} \\ &{n=38} &{1^\text{st} \text{integer}}\end{aligned}\) \(\begin{aligned} &{n+2} & &{2^\text{nd} \text{integer}}\\ &{38+2} \\ &{40} \end{aligned}\) \(\begin{aligned} &{n+2} & &{3^\text{rd} \text{integer}}\\ &{38+4} \\ &{42} \end{aligned}\) |
| 第 6 步。 查看。 \(\begin{align*} 38 + 40 + 42 &\overset{?}{=} &120 \nonumber\\ 120 &=& 120 &✓ \nonumber\end{align*}\) | |
| 第 7 步。 回答问题。 | 三个连续的整数分别为 38、40 和 42。 |
找出三个连续的偶数整数,其总和为 102。
- 回答
-
\(32, 34, 36\)
找出三个连续的偶数整数,其总和为\(−24\)。
- 回答
-
\(−10,−8,−6\)
当数字问题出现在现实生活中时,我们仍然使用与前面示例相同的策略。
一对已婚夫妇每年的总收入为110,000美元。 妻子的收入少16,000美元,不到丈夫收入的两倍。 丈夫挣多少钱?
解决方案:
| 第 1 步。 阅读问题。 | |
| 第 2 步。 确定你在找什么。 | 丈夫挣多少钱? |
| 第 3 步。 分别命名三个数字 |
让\(h=\text{the amount the husband earns}\)。 |
| 第 4 步。 翻译。
用一句话用所有重要信息重述问题。 翻译成方程式。 |
\(2h−16,000=\text{the amount the wife earns}.\)夫妻共赚110,000美元。 \(h+2h−16,000=110,000\) |
| 第 5 步。 求解方程。
将相似的术语组合在一起。 在两边增加 16,000 然后简化。 将每边除以三。 |
\(h+2h−16,000=110,000\) \(\begin{aligned} &{3h−16,000=110,000} \\ &{3h=126,000} \\ &{h=42,000} &{\text{amount husband earns}} \end{aligned}\) \(\begin{aligned} &{2h−16,000} &{\text{ amount wife earns}} \\ &{2(42,000)−16,000} \\ &{84,000−16,000} \\ &{68,000} \end{aligned}\) |
| 第 6 步。 查看。 如果妻子的收入为68,000美元,而丈夫的收入为42,000美元,那是110,000美元吗? 是的! | |
| 第 7 步。 回答问题。 | 丈夫每年的收入为42,000美元。 |
根据全国汽车经销商协会的数据,2014年一辆汽车的平均成本为28,400美元。 这比1975年成本低了1600美元。 1975 年汽车的平均成本是多少?
- 回答
-
平均成本为5,000美元。
美国人口普查数据显示,2014年11月美国新房的中位价为280,900美元。 这比1964年11月的价格高出10,700美元,是价格的14倍。 1964 年 11 月新房的中位价是多少?
- 回答
-
中位价为19,300美元。
求解百分比应用程序
有几种方法可以求解百分比方程。 在代数中,最简单的方法是将英语句子翻译成代数方程然后求解方程。 在方程中使用给定百分比之前,请务必将其更改为十进制。
翻译并解决:
- 84 个数字中的 45% 是多少?
- 4.76 美元是多少金额的 8.5%?
- 168 是 112 的百分比是多少?
解决方案:
一个。
 |
|
| 翻译成代数。 假设 n = 数字。 | 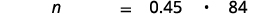 |
| 乘以。 | 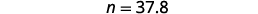 |
| 37.8 是 84 中的 45%。 |
b。
 |
|
| 翻译。 让\(n =\)金额。 | 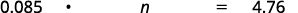 |
| 乘以。 | 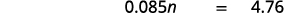 |
| 将两边除以 0.085 然后简化。 |  |
| 56 美元中的 8.5% 为 4.76 美元 |
c。
| 我们被要求找到百分比,所以我们必须以百分比形式得出结果。 |  |
| 翻译成代数。 让\(p = \)百分比。 | 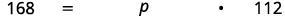 |
| 乘以。 |  |
| 将两边除以 112 然后简化。 | .jpg) |
| 转换为百分比。 |  |
| 168 是 112 中的 150%。 |
翻译并解决:
- 80 中的 45% 是多少?
- 多少金额的7.5%是1.95美元?
- 110 是 88 的百分比是多少?
- 回答
-
a. 36 b. 26 c.\(125 \% \)
翻译并解决:
- 60 个数字中的 55% 是多少?
- 3.06美元是多少金额的8.5%?
- 126 是 72 的百分比是多少?
- 回答
-
a. 33 b. 36 c.\(175 \% \)
现在我们有了问题解决策略可供参考,并且已经练习了求解基本的百分比方程,我们已经准备好求解百分比应用程序了。 一定要问问自己,你的最终答案是否有意义——因为我们将要解决的许多应用程序都涉及日常情况,所以你可以依靠自己的经验。
奥黛丽酸奶的标签上写着,一份含有12克蛋白质,占每日建议摄入量的24%。 建议的每日蛋白质总量是多少?
解决方案:
| 你要找什么? | 推荐的蛋白质总量是多少? |
| 选择一个变量来表示它。 | 让\(a=\)总量的蛋白质。 |
| 写一句话,给出找到它的信息。 | 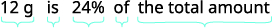 |
| 翻译成方程式。 |  |
| 解决。 |  |
| 查看:这有意义吗? 是的,24%约\(\frac{1}{4}\)占总数,12%约\(\frac{1}{4}\)占50%。 | |
| 写一个完整的句子来回答这个问题。 | 推荐的蛋白质含量为50 g。 |
一份小麦方麦片含有7克纤维,占每日建议摄入量的28%。 建议的每日纤维总量是多少?
- 回答
-
25 克
一份米粉含有 190 毫克钠,相当于每日建议摄入量的8%。 建议的每日钠总量是多少?
- 回答
-
2,375 毫克
记得按要求填写答案。 在下一个示例中,我们正在寻找百分比。
维罗妮卡正计划用混合物制作松饼。 包装上说每个松饼将含有240卡路里的热量,60卡路里将来自脂肪。 总卡路里中有多少百分比来自脂肪?
解决方案:
| 你要找什么? | 总卡路里中有多少百分比是脂肪? |
| 选择一个变量来表示它。 | 让\(p=\)百分比的脂肪。 |
| 写一句话,给出找到它的信息。 |  |
| 将句子翻译成方程式。 |  |
| 乘以。 |  |
| 将两边除以 240。 |  |
| 以百分比形式输入。 |  |
| 查看:这有意义吗? 是的,\(25 \% \)是四分之一;60 是 240 中的四分之一。 所以,这是有\(25 \%\)道理的。 | |
| 写一个完整的句子来回答这个问题。 | 在每个松饼的总卡路里中,\(25 \%\)有脂肪。 |
Mitzi 收到了一些美味的布朗尼作为礼物。 包装纸说每28%的布朗尼含有480卡路里的热量,并且含有240卡路里的脂肪。 每个布朗尼的总卡路里中有多少百分比来自脂肪? 将答案四舍五入到最接近的整数百分比。
- 回答
-
50%
里卡多计划用来制作布朗尼蛋糕的混合物说,每个布朗尼将含有190卡路里的热量,76卡路里来自脂肪。 总卡路里中有多少百分比来自脂肪? 将答案四舍五入到最接近的整数百分比。
- 回答
-
40%
在商业、科学、流行文化等许多领域,谈论一段时间内金额增加或减少了多少通常很重要。 这种增加或减少通常以百分比表示,称为百分比变化。
要找到百分比变化,首先我们通过找到新金额和原始金额的差额来找到变化金额。 然后我们找出变动金额占原始金额的百分比。
- 找出零钱的金额。
\[\text{change}= \text{new amount}−\text{original amount}\]
- 找出变动金额占原始金额的百分比。
变化是原始金额的多少百分比?
最近,加利福尼亚州州长提议将社区大学的学费从每单位36美元提高到每单位46美元。 找出百分比变化。 (四舍五入到最接近的百分之一的十分之一。)
解决方案:
| 找出零钱的金额。 | \(46−36=10\) |
| 找到百分比。 | 变化是原始金额的多少百分比? |
| 让\(p=\)百分比。 |  |
| 转换为方程。 | 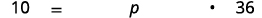 |
| 简化。 | \(10=36 p\) |
| 将两边除以 36。 | \(0.278 \approx p\) |
| 更改为百分比格式;四舍五入到最接近的十分之一 | \(27.8 \% \approx p\) |
| 写一个完整的句子来回答这个问题。 | 与旧费用相比,新费用大约\(27.8 \% \)有所增加。 |
| 记得将除法四舍五入到最接近的千分之一,以便将百分比四舍五入到最接近的十分之一。 | |
找出百分比变化。 (四舍五入到最接近的百分之一的十分之一。) 2011年,美国国税局将免赔里程费用从51美分提高到55.5美分。
- 回答
-
\(8.8 \% \)
找出百分比变化。 (四舍五入到最接近的百分之一的十分之一。) 1995 年,芝加哥的标准公交车票价为 1.50 美元。 2008 年,标准公交车票价为 2.25。
- 回答
-
\(50%\)
折扣和加价的应用在零售环境中非常常见。
当您购买特价商品时,原价已折扣一定金额。 折扣率通常以百分比给出,用于确定折扣金额。 为了确定折扣金额,我们将折扣率乘以原始价格。
零售商为一件商品支付的价格称为原始成本。 然后,零售商在原始成本上加一个加价以获得标价,即他出售该商品的价格。 加价通常按原始成本的百分比计算。 要确定加价金额,请将加价率乘以原始成本。
\[ \begin{align*} \text{amount of discount} &= \text{discount rate}· \text{original price} \\ \text{sale price} &= \text{original amount}– \text{discount price} \end{align*}\]
销售价格应始终低于原始价格。
\[\begin{align*} \text{amount of mark-up} &= \text{mark-up rate}·\text{original price} \\ \text{list price} &= \text{original cost}–\text{mark-up} \end{align*}\]
标价应始终高于原始成本。
利亚姆的美术馆以750美元的原价购买了一幅画。 利亚姆将价格上涨了40%。 查找
- 加价金额和
- 这幅画的标价。
解决方案:
一个。
| 确定要求您查找的内容,然后选择一个变量来表示它。 | 加价金额是多少? 让\(m=\)加价金额增加。 |
| 写一句话,给出找到它的信息。 | 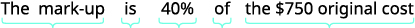 |
| 翻译成方程式。 |  |
| 求解方程。 |  |
| 写一个完整的句子。 | 这幅画的加价为300美元。 |
| 确定要求您查找的内容,然后选择一个变量来表示它。 | 标价是多少? 让\(p=\)标价出去。 |
| 写一句话,给出找到它的信息。 |  |
| 翻译成方程式。 | 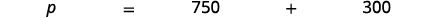 |
| 求解方程。 |  |
| 查看。 | 标价是否高于原始成本? 1,050 美元比 750 美元多吗? 是的。 |
| 写一个完整的句子。 | 这幅画的标价为1,050美元。 |
找到 a. 加价金额和 b. 标价:吉姆的音乐商店以原价1200美元买了一把吉他。 吉姆标价上涨了50%。
- 回答
-
a. 600亿美元。1,800美元
找到 a. 加价金额和 b. 标价:汽车转售商店以 8,500 美元的价格收购了 Pablo 的丰田汽车。 他们将价格上涨了35%。
- 回答
-
a. 2,975 美元。11,475 美元
解决简单利息申请
兴趣是我们日常生活的一部分。 从储蓄赚取的利息到我们为汽车贷款或信用卡债务支付的利息,我们都有一些生活利息的经验。
您最初存入银行的金额称为本金,\(P,\)银行向您支付利息。\(I.\)当您贷款时,您需要为借入的金额(也称为本金)支付利息。
无论哪种情况,利息都是按本金的某个百分比计算的,称为利率。利率通常以每年的百分比表示,并使用百分比的十进制等值来计算。\(r.\) 变量\(t,\)(代表时间)表示存钱或借钱的年数。
利息按单利或复利计算。 这里我们将使用简单利息。
如果按\(t\)年利率\(r,\)投资或借入一笔\(P,\)称为本金的金额,则\(I,\)赚取或支付的利息金额为
\[ \begin{array}{ll} I=Prt \; \; \; \; \; \; \; \; \; \; \; \; \text{where} & { \begin{align*} I &= \text{interest} \\ P &= \text{principal} \\ r &= \text{rate} \\ t &= \text{time} \end{align*}} \end{array}\]
根据此公式赚取或支付的利息称为简单利息。
我们用来计算利息的公式是\(I=Prt\)。 要使用公式,我们在给定变量的值中替换,然后求解未知变量。 在图表中组织信息可能会有所帮助。
阿雷利在她的银行账户中投资了950美元的本金,该账户以3%的利率赚取了简单利息。 她在五年内赚了多少利息?
解决方案:
\( \begin{aligned} I & = \; ? \\ P & = \; \$ 950 \\ r & = \; 3 \% \\ t & = \; 5 \text{ years} \end{aligned}\)
\(\begin{array}{ll} \text{Identify what you are asked to find, and choose a} & \text{What is the simple interest?} \\ \text{variable to represent it.} & \text{Let } I= \text{interest.} \\ \text{Write the formula.} & I=Prt \\ \text{Substitute in the given information.} & I=(950)(0.03)(5) \\ \text{Simplify.} & I=142.5 \\ \text{Check.} \\ \text{Is } \$142.50 \text{ a reasonable amount of interest on } \$ \text{ 950?} \; \;\;\;\;\; \;\;\;\;\;\; \\ \text{Yes.} \\ \text{Write a complete sentence.} & \text{The interest is } \$ \text{142.50.} \end{array}\)
娜塔莉在她的银行账户中存入了12,500美元,在那里可以赚取4%的简单利息。 纳塔利在五年内能赚多少利息?
- 回答
-
他将获得 2,500 美元。
苏珊娜在她的银行账户中投资了36,000美元的本金,该账户以6.5%的利率赚取了简单利息。 她在三年内赚了多少利息?
- 回答
-
她赚了7,020美元。
有时我们可能知道给定本金在一定时间内赚取的利息金额,但我们不知道利率。
Hang 从父母那里借了 7,500 美元来支付学费。 在五年内,除了借入的7,500美元外,她还向他们支付了1,500美元的利息。 简单利率是多少?
解决方案:
\( \begin{aligned} I & = \; \$ 1500 \\ P & = \; \$ 7500 \\ r & = \; ? \\ t & = \; 5 \text{ years} \end{aligned}\)
\ (\ text {确定你被要求查找的内容,}\ qquad\ quad\ text {什么是简单利率?} \\
\ begin {align*}
&\ text {然后选择一个变量来表示它。} &\ text {Let} r\; &=\;\ text {利率}\\
&\ text {写下公式。} & I\; &=\; Prt\\
&\ text {在给定信息中替换。} & 1,500\; &=\; (7,500) r (5)\\
&\ text {乘以。} & 1,500\; &=\; 37,500r\\
&\ text {Divide。} & 0.04\; &=\; r\\
&\ text {更改为百分比形式} & r\; &=\; 4\%
\ end {align*}\)
查看。
\ (\ begin {align*} I\; &=\; Prt\\
1,500\; &\ stackrel {?} {=}\; (7,500) (0.04) (5)\\
1,500\; &=\; 1,500 ✓\ end {align*}\)
写一个完整的句子。 利率是\(4\%.\)
吉姆借给姐姐5000美元帮她买房。 在三年内,她向他支付了5,000美元,外加900美元的利息。 简单利率是多少?
- 回答
-
简单利率为6%。
洛伦借给他哥哥3000美元,帮助他买车。 四年来,他的兄弟向他偿还了3,000美元加上660美元的利息。 简单利率是多少?
- 回答
-
简单利率为5.5%。
在下一个示例中,我们被要求找到本金——借入的金额。
肖恩的新汽车贷款声明说,他将在五年内从8.5%的简单利率中支付4,866,25美元的利息。 他借了多少钱买新车?
解决方案:
\( \begin{aligned} I & = \; 4,866.25 \\ P & = \; ? \\ r & = \; 8.5 \% \\ t & = \; 5 \text{ years} \end{aligned}\)
\ (\ text {确定你被要求查找的内容,}\ qquad\ quad\ text {借款金额是多少(本金)?} \\
\ begin {align*}
&\ text {然后选择一个变量来表示它。} &\ text {Let} P\; &=\;\ text {校长借来了}\\
&\ text {写下公式。} & I\; &=\; Prt\\
&\ text {在给定信息中替换。} & 4,866.25\; &=\; P (0.085) (5)\\
&\ text {乘以。} & 4,866.25\; &=\; 0.425P\\
&\ text {Divide。} & 11,450\; &=\; P
\ end {align*}\)
查看。
\ (\ begin {align*} I\; &=\; Prt\\
4,866.25\; &\ stackrel {?} {=}\; (11,450) (0.085) (5)\\
4,866.25\; &=\; 4,866.25 ✓\ end {align*}\)
写一个完整的句子。 校长是\($11,450.\)
爱德华多注意到,他的新车贷款文件显示,如果简单利率为7.5%,他将在五年内支付6,596.25美元的利息。 他借了多少钱买车?
- 回答
-
他支付了17,590美元。
在五年内,格洛丽亚的银行账户赚取了2400美元的利息,单息为5%。 她在账户里存了多少钱?
- 回答
-
她存入了9,600美元。
访问此在线资源,获取更多指导和使用问题解决策略的练习。
- 开始算术问题
关键概念
- 如何使用问题解决策略来解决单词问题
- 阅读问题。 确保所有文字和想法都被理解。
- 确定你在找什么。
- 说出你要找的东西。 选择一个变量来表示该数量。
- 翻译成方程式。 用一句话用所有重要信息重述问题可能会有所帮助。 然后,将英语句子翻译成代数方程。
- 使用正确的代数技术求@@ 解方程。
- 检查问题中的答案以确保答案合理。
- 用完整的句子@@ 回答问题。
- 如何找到百分比变化
- 找出零钱金额
\(\text{change}=\text{new amount}−\text{original amount}\)
- 找出变动金额占原始金额的百分比。
\(\text{change is what percent of the original amount?}\)
- 找出零钱金额
- \( \begin{align*} \text{amount of discount} &= \text{discount rate}· \text{original price} \\ \text{sale price} &= \text{original amount}– \text{discount price} \end{align*}\)
- \(\begin{align*} \text{amount of mark-up} &= \text{mark-up rate}·\text{original price} \\ \text{list price} &= \text{original cost}–\text{mark-up} \end{align*}\)
- 如果按年利率\(r,\)投资或借入一笔\(P,\)称为本金的款项,为期 t 年,则\(I,\)赚取或支付的利息金额为:\[\begin{aligned} &{} &{} &{I=interest} \nonumber\\ &{I=Prt} &{\text{where} \space} &{P=principal} \nonumber\\ &{} &{\space} &{r=rate} \nonumber\\ &{} &{\space} &{t=time} \nonumber \end{aligned}\]