1.6E：练习

Last updated
Save as PDF

Page ID: 203951

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\dsum}{\displaystyle\sum\limits} $

$ \newcommand{\dint}{\displaystyle\int\limits} $

$ \newcommand{\dlim}{\displaystyle\lim\limits} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$\newcommand{\longvect}{\overrightarrow}$

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

练习成就完美

使用交换和关联属性

在以下练习中，简化。

1。 $43m+(−12n)+(−16m)+(−9n)$

回答: $27m+(−21n)$

2。 $−22p+17q+(−35p)+(−27q)$

3。 $\frac{3}{8}g+\frac{1}{12}h+\frac{7}{8}g+\frac{5}{12}h$

回答: $\frac{5}{4}g+\frac{1}{2}h$

4。 $\frac{5}{6}a+\frac{3}{10}b+\frac{1}{6}a+\frac{9}{10}b$

5。 $6.8p+9.14q+(−4.37p)+(−0.88q)$

回答: $2.43p+8.26q$

6。 $9.6m+7.22n+(−2.19m)+(−0.65n)$

7。 $−24·7·\frac{3}{8}$

回答: $−63$

8。 $−36·11·\frac{4}{9}$

9。 $\left(\frac{5}{6}+\frac{8}{15}\right)+\frac{7}{15}$

回答: $1\frac{5}{6}$

10。 $\left(\frac{11}{12}+\frac{4}{9}\right)+\frac{5}{9}$

11。 $17(0.25)(4)$

回答: $17$

12。 $36(0.2)(5)$

13。 $[2.48(12)](0.5)$

回答: $14.88$

14。 $[9.731(4)](0.75)$

15。 $12\left(\frac{5}{6}p\right)$

回答: $10p$

16。 $20\left(\frac{3}{5}q\right)$

使用恒等式、逆向和零的属性

在以下练习中，简化。

17。 $19a+44−19a$

回答: $44$

18。 $27c+16−27c$

19。 $\frac{1}{2}+\frac{7}{8}+\left(−\frac{1}{2}\right)$

回答: $\frac{7}{8}$

20。 $\frac{2}{5}+\frac{5}{12}+\left(−\frac{2}{5}\right)$

21。 $10(0.1d)$

回答: $d$

22。 $100(0.01p)$

23。 $\frac{3}{20}·\frac{49}{11}·\frac{20}{3}$

回答: $\frac{49}{11}$

24。 $\frac{13}{18}·\frac{25}{7}·\frac{18}{13}$

25。 $\frac{0}{u−4.99}$，哪里$u\neq 4.99$

回答: $0$

26。 $0÷(y−\frac{1}{6})$，哪里$x \neq 16$

27。 $\frac{32−5a}{0}$，哪里$32−5a\neq 0$

回答: 未定义

28。 $\frac{28−9b}{0}$，哪里$28−9b\neq 0$

29。 $\left(\frac{3}{4}+\frac{9}{10}m\right)÷0$，哪里$\frac{3}{4}+\frac{9}{10}m\neq 0$

回答: 未定义

30。 $\left(\frac{5}{16}n−\frac{3}{7}\right)÷0$，哪里$\frac{5}{16}n−\frac{3}{7}\neq 0$

使用分布属性简化表达式

在以下练习中，简化分布属性的使用。

31。 $8(4y+9)$

回答: $32y+72$

32。 $9(3w+7)$

33。 $6(c−13)$

回答: $6c−78$

34。 $7(y−13)$

35。 $\frac{1}{4}(3q+12)$

回答: $\frac{3}{4}q+3$

36。 $\frac{1}{5}(4m+20)$

37。 $9(\frac{5}{9}y−\frac{1}{3})$

回答: $5y−3$

38。 $10(\frac{3}{10}x−\frac{2}{5})$

39。 $12(\frac{1}{4}+\frac{2}{3}r)$

回答: $3+8r$

40。 $12(\frac{1}{6}+\frac{3}{4}s)$

41。 $15⋅\frac{3}{5}(4d+10)$

回答: $36d+90$

42。 $18⋅\frac{5}{6}(15h+24)$

43。 $r(s−18)$

回答: $rs−18r$

44。 $u(v−10)$

45。 $(y+4)p$

回答: $yp+4p$

46。 $(a+7)x$

47。 $−7(4p+1)$

回答: $−28p−7$

48。 $−9(9a+4)$

49。 $−3(x−6)$

回答: $−3x+18$

50。 $−4(q−7)$

51。 $−(3x−7)$

回答: $−3x+7$

52。 $−(5p−4)$

53。 $16−3(y+8)$

回答: $−3y−8$

54。 $18−4(x+2)$

55。 $4−11(3c−2)$

回答: $−33c+26$

56。 $9−6(7n−5)$

57。 $22−(a+3)$

回答: $−a+19$

58。 $8−(r−7)$

59。 $(5m−3)−(m+7)$

回答: $4m−10$

60。 $(4y−1)−(y−2)$

61。 $9(8x−3)−(−2)$

回答: $72x−25$

62。 $4(6x−1)−(−8)$

63。 $5(2n+9)+12(n−3)$

回答: $22n+9$

64。 $9(5u+8)+2(u−6)$

65。 $14(c−1)−8(c−6)$

回答: $6c+34$

66。 $11(n−7)−5(n−1)$

67。 $6(7y+8)−(30y−15)$

回答: $12y+63$

68。 $7(3n+9)−(4n−13)$

写作练习

69。用你自己的话说，陈述加法的关联属性。

回答: 答案会有所不同。

70。一个数字的加法逆和乘法逆有什么区别

71。简化分布属性的$8(x−\frac{1}{4})$使用并解释每个步骤。

回答: 答案会有所不同。

72。解释如何在$4($5.97)$没有纸张或计算器的情况下进行乘法，方法是先考虑 a$$5.97$ s$6−0.03$ 然后使用分布属性。

自检

a. 完成练习后，使用此清单评估您对本节目标的掌握程度。

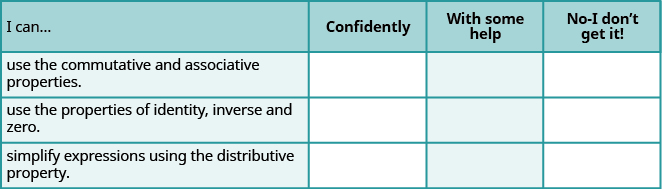
$此表有 4 列、3 行和一个标题行。标题行在一些帮助下自信地标记了我能做到的每一列，不，我不明白。第一列有以下语句：使用交换和关联属性，使用恒等属性、反向和零属性，使用分布属性简化表达式。其余列为空白。$

b. 看完这份清单后，你会怎么做才能对所有目标充满信心？