第 1 章复习练习

章节复习练习

使用代数语言

识别倍数和因子

1。 使用可分性测试确定 180 是否可被 2、3、5、6 和 10 整除。

回答

可分割为\(2,3,5,6\)

2。 求出 252 的素数因式分解。

3。 找出 24 和 40 的最小公倍数。

回答

120

在以下练习中，简化每个表达式。

4。 \(24÷3+4(5−2)\)

5。 \(7+3[6−4(5−4)]−3^2\)

回答

4

计算表达式

在以下练习中，计算以下表达式。

6。 什么时候\(x=4\), ⓐ \(x^3\) ⓑ \(5x\) ⓒ \(2x^2−5x+3\)

7。 \(2x^2−4xy−3y^2\)何时\(x=3\)和\(y=1\)

回答

3

通过组合相似术语来简化表达式

在以下练习中，通过组合相似术语来简化以下表达式。

8。 \(12y+7+2y−5\)

9。 \(14x^2−9x+11−8x^2+8x−6\)

回答

\(6x^2−x+5\)

将英语短语翻译成代数表达式

在以下练习中，将短语翻译成代数表达式。

10. ⓐ 和 and 之\(4ab^2\)\(7a3b24ab^2\)和\(7a^3b^2\)

ⓑ\(6y^2\) 和的产物\(3y\)

ⓒ 比十二多\(5x\)

ⓓ\(5y\) 小于\(8y^2\)

11. ⓐ 差值的十一倍\(y\)和两倍

ⓑ 十一倍\(y\)和二的差异

回答

ⓐ\(11(y−2)\)
ⓑ\(11y−2\)

12。 杜什科的口袋里有镍和便士。 便士的数量比镍的数量少四个。 假设 nn 代表镍的数量。 为便士数写一个表达式。

整数

使用绝对值简化表达式

在以下练习中，\(=\)为以下每对数字填写\(<,>,\)或。

13. ⓐ\(−|7| \_\_\_−|−7|\)

ⓑ\(−8 \_\_\_−|−8|\)

ⓒ\(|−13| \_\_\_−13\)

ⓓ\(|−12| \_\_\_−(−12)\)

回答

ⓐ\(=\)
ⓑ\(=\)
ⓒ\(>\)
ⓓ\(=\)

在以下练习中，进行简化。

14。 \(9−|3(4−8)|\)

15。 \(12−3|1−4(4−2)|\)

回答

\(−9\)

加减整数

在以下练习中，简化每个表达式。

16。 \(−12+(−8)+7\)

17. ⓐ\(15−7\)

ⓑ\(−15−(−7)\)

ⓒ\(−15−7\)

ⓓ\(15−(−7)\)

回答

ⓐ\(8\)
ⓑ\(−8\)
ⓒ\(−22\)
ⓓ\(22\)

18。 \(−11−(−12)+5\)

19. ⓐ\(23−(−17)\) ⓑ\(23+17\)

回答

ⓐ 40 ⓑ 40

20。 \(−(7−11)−(3−5)\)

乘以和除以整数

在以下练习中，乘以或除法。

21. ⓐ\(−27÷9\) ⓑ\(120÷(−8)\) ⓒ\(4(−14)\) ⓓ\(−1(−17)\)

回答

ⓐ\(−3\) ⓑ\(−15\) ⓒ\(−56\) ⓓ\(17\)

使用整数简化和计算表达式

在以下练习中，简化每个表达式。

22. ⓐ\((−7)^3\) ⓑ\(−7^3\)

23。 \((7−11)(6−13)\)

回答

16

24。 \(63÷(−9)+(−36)÷(−4)\)

25。 \(6−3|4(1−2)−(7−5)|\)

回答

\(−12\)

26。 \((−2)^4−24÷(13−5)\)

在以下练习中，计算每个表达式。

27。 \((y+z)^2\)何时\(y=−4\)和\(z=7\)

回答

9

28。 \(3x^2−2xy+4y^2\)何时\(x=−2\)和\(y=−3\)

将英语短语翻译成代数表达式

在以下练习中，翻译成代数表达式并尽可能简化。

29.\(−4\) 和之和\(−9\)，乘以\(23\)

回答

\((−4+(−9))+23;10\)

30. ⓐ 17 和 −8 的差 ⓑ 从 −25 中减去 17

在应用程序中使用整数

在以下练习中，求解。

31。 温度7月10日，亚利桑那州凤凰城的高温为109度，阿拉斯加朱诺的高温为63度。 棕榈泉的温度和怀特菲尔德的温度有什么区别？

回答

\(46°\)

分数

简化分数

在以下练习中，简化。

32。 \(\dfrac{204}{228}\)

33。 \(−\dfrac{270x^3}{198y^2}\)

回答

\(−\dfrac{15x^3}{11y^2}\)

乘以和除以分数

在以下练习中，执行指定的操作。

34。 \(\left(−\dfrac{14}{15}\right)\left(\dfrac{10}{21}\right)\)

35。 \(\dfrac{6x}{25}÷\dfrac{9y}{20}\)

回答

\(\dfrac{8x}{15y}\)

36。 \(\dfrac{−\frac{4}{9}}{\dfrac{8}{21}}\)

加减分数

在以下练习中，执行指定的操作。

37。 \(\dfrac{5}{18}+\dfrac{7}{12}\)

回答

\(\dfrac{31}{36}\)

38。 \(\dfrac{11}{36}−\dfrac{15}{48}\)

39. ⓐ\(\dfrac{5}{8}+\dfrac{3}{4}\) ⓑ\(\dfrac{5}{8}÷\dfrac{3}{4}\)

回答

ⓐ\(\dfrac{11}{8}\) ⓑ\(\dfrac{5}{6}\)

40. ⓐ\(−\dfrac{3y}{10}−\dfrac{5}{6}\) ⓑ\(−\dfrac{3y}{10}·\dfrac{5}{6}\)

使用运算顺序简化分数

在以下练习中，简化。

41。 \(\dfrac{4·3−2·5}{−6·3+2·3}\)

回答

\(−\dfrac{1}{6}\)

42。 \(\dfrac{4(7−3)−2(4−9)}{−3(4+2)+7(3−6)}\)

43。 \(\dfrac{4^3−4^2}{(\dfrac{4}{5})^2}\)

回答

75

使用分数计算变量表达式

在以下练习中，进行评估。

44。 \(4x^2y^2\)何时\(x=\dfrac{2}{3}\)和\(y=−\dfrac{3}{4}\)

45。 \(\dfrac{a+b}{a−b}\)何时\(a=−4\)和\(b=6\)

回答

\(−15\)

小数

四舍五进制小数

46。 四舍五入\(6.738\)到最接近的 ⓐ 第一百 ⓑ 十 ⓒ 整数。

加减小数

在以下练习中，执行指定的操作。

47。 \(−23.67+29.84\)

回答

\(6.17\)

48。 \(54.3−100\)

49。 \(79.38−(−17.598)\)

回答

\(96.978\)

乘以和除以小数

在以下练习中，执行指定的操作。

50。 \((−2.8)(3.97)\)

51。 \((−8.43)(−57.91)\)

回答

488.1813

52。 \((53.48)(10)\)

53。 \((0.563)(100)\)

回答

\(56.3\)

54。 \( \$ 118.35÷2.6\)

55。 \(1.84÷(−0.8)\)

回答

\(−23\)

转换小数、分数和百分比

在以下练习中，将每个小数写成分数。

56。 \(\dfrac{13}{20}\)

57。 \(−\dfrac{240}{25}\)

回答

\(−9.6\)

在以下练习中，将每个分数转换为十进制。

58。 \(−\dfrac{5}{8}\)

59。 \(\dfrac{14}{11}\)

回答

\(1.\overline{27}\)

在以下练习中，将每个小数转换为百分比。

60。 \(2.43\)

61。 \(0.0475\)

回答

\(4.75 \% \)

使用平方根简化表达式

在以下练习中，简化。

62。 \(\sqrt{289}\)

63。 \(\sqrt{−121}\)

回答

没有实数

识别整数、有理数、非理数和实数

在以下练习中，列出 ⓐ 整数 ⓑ 整数 ⓒ 有理数 ⓓ 无理数 ⓔ 每组数字的实数

64。 \(−8,0,1.95286...,\dfrac{12}{5},\sqrt{36},9\)

在数字行上找到分数和小数

在以下练习中，在数字行上找到数字。

65。 \(\dfrac{3}{4},−\dfrac{3}{4},1\dfrac{1}{3},−1\dfrac{2}{3},\dfrac{7}{2},−\dfrac{5}{2}\)

回答

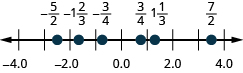
66. ⓐ\(3.2\) ⓑ\(−1.35\)

实数的属性

使用交换和关联属性

在以下练习中，简化。

67。 \(\dfrac{5}{8}x+\dfrac{5}{12}y+\dfrac{1}{8}x+\dfrac{7}{12}y\)

回答

\(\dfrac{3}{4}x+y\)

68。 \(−32·9·\dfrac{5}{8}\)

69。 \(\left(\dfrac{11}{15}+\dfrac{3}{8}\right)+\dfrac{5}{8}\)

回答

\(1\dfrac{11}{15}\)

使用恒等式、逆向和零的属性

在以下练习中，简化。

70。 \(\dfrac{4}{7}+\dfrac{8}{15}+\left(−\dfrac{4}{7}\right)\)

71。 \(\dfrac{13}{15}·\dfrac{9}{17}·\dfrac{15}{13}\)

回答

\(\dfrac{9}{17}\)

72。 \(\dfrac{0}{x−3},x\neq 3\)

73。 \(\dfrac{5x−7}{0},5x−7\neq 0\)

回答

未定义

使用分布属性简化表达式

在以下练习中，简化分布属性的使用。

74。 \(8(a−4)\)

75。 \(12\left(\dfrac{2}{3}b+\dfrac{5}{6}\right)\)

回答

\(8b+10\)

76。 \(18·\dfrac{5}{6}(2x−5)\)

77。 \((x−5)p\)

回答

\(xp−5p\)

78。 \(−4(y−3)\)

79。 \(12−6(x+3)\)

回答

\(−6x−6\)

80。 \(6(3x−4)−(−5)\)

81。 \(5(2y+3)−(4y−1)\)

回答

\(y+16\)

练习测试

1。 找到的素数因式分解\(756\)。

2。 将类似的术语组合在一起：\(5n+8+2n−1\)

回答

\(7n+7\)

3。 评估何时\(x=−2\)和\(y=3: \dfrac{|3x−4y|}{6}\)

4。 翻译成代数表达式并简化：

ⓐ 十一小于负八

ⓑ\(−8\) 和之差\(−3\)，增加 5

回答

\(−8−11 = −19\)
\((−8−(−3))+5 = 0\)

5。 杜什科的口袋里有镍和便士。 便士的数量比镍数少四倍的七个。 假设 nn 代表镍的数量。 为便士数写一个表达式。

6。 四舍五\(28.1458\)入到最近的

ⓐ 第一百 ⓑ 千分之一

回答

ⓐ\(28.15\) ⓑ\(28.146\)

7。 转换

ⓐ\(\dfrac{5}{11}\) 到十进制 ⓑ\(1.15\) 到百分比

8。 在数字行\(\dfrac{3}{5},2.8,and−\dfrac{5}{2}\)上找到。

回答

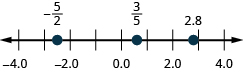
在以下练习中，简化每个表达式。

9。 \(8+3[6−3(5−2)]−4^2\)

10。 \(−(4−9)−(9−5)\)

回答

1

11。 \(56÷(−8)+(−27)÷(−3)\)

12。 \(16−2|3(1−4)−(8−5)|\)

回答

\(−8\)

13。 \(−5+2(−3)^2−9\)

14。 \(\dfrac{180}{204}\)

回答

\(\dfrac{15}{17}\)

15。 \(−\dfrac{7}{18}+\dfrac{5}{12}\)

16。 \(\dfrac{4}{5}÷(−\dfrac{12}{25})\)

回答

\(−\dfrac{5}{3}\)

17。 \(\dfrac{9−3·9}{15−9}\)

18。 \(\dfrac{4(−3+2(3−6))}{3(11−3(2+3))}\)

回答

\(3\)

19。 \(\dfrac{5}{13}⋅\dfrac{4}{7}⋅\dfrac{13}{5}\)

20。 \(\dfrac{−\dfrac{5}{9}}{\dfrac{10}{21}}\)

回答

\(−\dfrac{7}{6}\)

21。 \(−4.8+(−6.7)\)

22。 \(34.6−100\)

回答

\(−65.4\)

23。 \(−12.04⋅(4.2)\)

24。 \(−8÷0.05\)

回答

160

25。 \(−\sqrt{121}\)

26。 \((\dfrac{8}{13}+\dfrac{5}{7})+\dfrac{2}{7}\)

回答

\(1\dfrac{8}{13}\)

27。 \(5x+(−8y)−6x+3y\)

28. ⓐ\(\dfrac{0}{9}\) ⓑ\(\dfrac{11}{0}\)

回答

ⓐ 0 ⓑ 未定义

29。 \(−3(8x−5)\)

30。 \(6(3y−1)−(5y−3)\)

回答

\(13y−3\)