1.6: 实数的属性
- Page ID
- 203944
在本节结束时,您将能够:
- 使用交换和关联属性
- 使用恒等式、反向和零的属性
- 使用分布属性简化表达式
使用交换和关联属性
我们将两个数字相加的顺序不会影响结果。 如果我们加上\(8+9\)或\(9+8\),结果是相同的,它们都等于 17。 所以,\(8+9=9+8\)。 我们添加的顺序无关紧要!
同样,将两个数字相乘时,顺序不会影响结果。 如果我们相乘\(9·8\)或者\(8·9\)结果相同,它们都等于 72。 所以,\(9·8=8·9\)。 我们乘以的顺序并不重要! 这些示例说明了可交换属性。
\[\begin{array}{lll} \textbf{of Addition} & \text{If }a \text{ and }b \text{are real numbers, then} & a+b=b+a. \\ \textbf{of Multiplication} & \text{If }a \text{ and }b \text{are real numbers, then} & a·b=b·a. \end{array} \]
相加或乘法时,更改顺序会得到相同的结果。
交换财产与秩序有关。 我们减去\(9−8\) and\(8−9\),然后看出来\(9−8\neq 8−9\)。 由于改变减法的顺序不会得到相同的结果,因此我们知道减法是不可交换的。
分区也不可交换。 因为\(12÷3\neq 3÷12\),改变除法顺序不会得出相同的结果。 交换属性仅适用于加法和乘法!
- 加法和乘法是可交换的。
- 减法和除法是不可交换的。
将三个数字相加时,更改数字的分组会得到相同的结果。 例如\((7+8)+2=7+(8+2)\),因为方程的每一边都等于 17。
乘法也是如此。 例如\(\left(5·\frac{1}{3}\right)·3=5·\left(\frac{1}{3}·3\right)\),因为方程的每一边等于 5。
这些示例说明了关联属性。
\[\begin{array}{lll} \textbf{of Addition} & \text{If }a,b, \text{ and }c \text{ are real numbers, then} & (a+b)+c=a+(b+c). \\ \textbf{of Multiplication} & \text{If }a,b,\text{ and }c \text{ are real numbers, then} & (a·b)·c=a·(b·c). \end{array} \]
相加或乘法时,更改分组会得到相同的结果。
关联属性与分组有关。 如果我们改变数字的分组方式,结果将相同。 请注意,这三个数字的顺序相同,唯一的区别是分组。
我们看到减法和除法是不可交换的。 它们也不是联想的。
\[\begin{array}{cc} (10−3)−2\neq 10−(3−2) & (24÷4)÷2\neq 24÷(4÷2) \\ 7−2\neq 10−1 & 6÷2\neq 24÷2 \\ 5\neq 9 & 3\neq 12 \end{array}\]
在简化表达式时,计划步骤总是一个好主意。 为了在下一个示例中组合相似的术语,我们将使用加法的可交换属性将相似的术语写在一起。
简化:\(18p+6q+15p+5q\)。
- 回答
-
\[\begin{array}{lc} \text{} & 18p+6q+15p+5q \\ \text{Use the Commutative Property of addition to} & 18p+15p+6q+5q \\ \text{reorder so that like terms are together.} & {} \\ \text{Add like terms.} & 33p+11q \end{array}\]
简化:\(23r+14s+9r+15s\)。
- 回答
-
\(32r+29s\)
简化:\(37m+21n+4m−15n\)。
- 回答
-
\(41m+6n\)
当我们必须简化代数表达式时,我们通常可以通过先应用可交换属性或关联属性来简化工作。
简化:\((\frac{5}{13}+\frac{3}{4})+\frac{1}{4}\)。
- 回答
-
\( \begin{array}{lc} \text{} & (\frac{5}{13}+\frac{3}{4})+\frac{1}{4} \\ {\text{Notice that the last 2 terms have a common} \\ \text{denominator, so change the grouping.} } & \frac{5}{13}+(\frac{3}{4}+\frac{1}{4}) \\ \text{Add in parentheses first.} & \frac{5}{13}+(\frac{4}{4}) \\ \text{Simplify the fraction.} & \frac{5}{13}+1 \\ \text{Add.} & 1\frac{5}{13} \\ \text{Convert to an improper fraction.} & \frac{18}{13} \end{array}\)
简化:\((\frac{7}{15}+\frac{5}{8})+\frac{3}{8}.\)
- 回答
-
\(1 \frac{7}{15}\)
简化:\((\frac{2}{9}+\frac{7}{12})+\frac{5}{12}\)。
- 回答
-
\(1\frac{2}{9}\)
使用恒等式、逆向和零的属性
当我们将0加到任何数字时会发生什么? 添加 0 不会更改该值。 出于这个原因,我们称0为加法恒等式。 加法的 I dentity Property 表示对于任何实数\(a,a+0=a\)和\(0+a=a.\)
当我们将任何数字乘以一时会发生什么? 乘以 1 不会改变该值。 所以我们称1为乘法恒等式。 乘法的身份属性,它指出对于任何实数\(a,a·1=a\)和\(1⋅a=a.\)
我们在此总结身份属性。
\[\begin{array}{ll} \textbf{of Addition} \text{ For any real number }a:a+0=a & 0+a=a \\ \\ \\ \textbf{0} \text{ is the } \textbf{additive identity} \\ \textbf{of Multiplication} \text{ For any real number } a:a·1=a & 1·a=a \\ \\ \\ \textbf{1} \text{ is the } \textbf{multiplicative identity} \end{array}\]
将哪个数字与 5 相加得出加法恒等号,0? 我们知道
.jpg)
缺少的数字与数字相反!
我们称之\(−a\)为的加法反向\(a\)。 与数字相反的是其相加的逆数。 一个数字及其对立方加起来为零,这是加法恒等式。 这就导致了加法的逆属性,它表示任何实数\(a,a+(−a)=0.\)
将哪个数字乘以得\(\frac{2}{3}\)出乘法恒等式,即 1? 换句话说,\(\frac{2}{3}\)乘以 1 的结果是多少? 我们知道
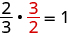
缺少的数字是该数字的倒数!
我们称\(\frac{1}{a}\)之为 a 的乘法逆函数。 数字@@ 的倒数是其乘法逆数。 这就产生了乘法的逆属性,它指出,对于任何实数\(a,a\neq 0,a·\frac{1}{a}=1.\)
我们将在这里正式陈述反向属性。
\[\begin{array}{lc} \textbf{of addition} \text{For any real number }a, & a+(−a)=0 \\ \;\;\;\; −a \text{ is the } \textbf{additive inverse }\text{ of }a & {} \\ \;\;\;\; \text{A number and its } \textit{opposite } \text{add to zero.} \\ \\ \\ \textbf{of multiplication } \text{For any real number }a,a\neq 0 & a·\dfrac{1}{a}=1 \\ \;\;\;\;\;\dfrac{1}{a} \text{ is the } \textbf{multiplicative inverse} \text{ of }a \\ \;\;\;\; \text{A number and its } \textit{reciprocal} \text{ multiply to one.} \end{array}\]
加法的 Identity Property 表示,当我们将 0 与任意数字相加时,结果是相同的数字。 当我们将一个数字乘以 0 时会发生什么? 乘以 0 使乘积等于零。
那涉及零的分割呢? 什么是\(0÷3\)? 想一个真实的例子:如果饼干罐里没有饼干,而要有三个人分享它们,那么每个人会得到多少饼干? 没有可共享的 cookie,因此每人获得 0 个 cookie。 所以,\(0÷3=0.\)
我们可以用相关的乘法数来检查除法。 所以我们知道是\(0÷3=0\)因为\(0·3=0\)。
现在考虑除以零。 将 4 除以 0 的结果是什么? 想想相关的乘法事实:

有没有一个数字乘以 0 得出 4? 由于任何实数乘以 0 都会得到 0,因此没有实数可以乘以 0 得到 4。 我们得出结论,没有答案\(4÷0\),所以我们说除以 0 是未定义的。
我们在这里总结零的属性。
乘以零:对于任何实数 a,
\[a⋅0=0 \; \; \; 0⋅a=0 \; \; \; \; \text{The product of any number and 0 is 0.}\]
除以零:对于任何实数 a,\(a\neq 0\)
\[\begin{array}{cl} \dfrac{0}{a}=0 & \text{Zero divided by any real number, except itself, is zero.} \\ \dfrac{a}{0} \text{ is undefined} & \text{Division by zero is undefined.} \end{array}\]
我们现在将练习使用恒等式、反向和零的属性来简化表达式。
简化:\(−84n+(−73n)+84n.\)
- 回答
-
\(\begin{array}{lc} \text{} & −84n+(−73n)+84n \\ \text{Notice that the first and third terms are} \\ \text{opposites; use the Commutative Property of} & −84n+84n+(−73n) \\ \text{addition to re-order the terms.} \\ \text{Add left to right.} & 0+(−73n) \\ \text{Add.} & −73n \end{array}\)
简化:\(−27a+(−48a)+27a\)。
- 回答
-
\(−48a\)
简化:\(39x+(−92x)+(−39x)\)。
- 回答
-
\(−92x\)
现在我们将看看承认互惠是如何有帮助的。 在从左到右乘法之前,先寻找倒数——它们的乘积为 1。
简化:\(\frac{7}{15}⋅\frac{8}{23}⋅\frac{15}{7}\)。
- 回答
-
\(\begin{array}{lc} \text{} & \frac{7}{15}⋅\frac{8}{23}⋅\frac{15}{7} \\ \text{Notice the first and third terms} \\ {\text{are reciprocals, so use the Commutative} \\ \text{Property of multiplication to re-order the} \\ \text{factors.}} & \frac{7}{15}·\frac{15}{7}·\frac{8}{23} \\ \text{Multiply left to right.} & 1·\frac{8}{23} \\ \text{Multiply.} & \frac{8}{23} \end{array}\)
简化:\(\frac{9}{16}⋅\frac{5}{49}⋅\frac{16}{9}\)。
- 回答
-
\(\frac{5}{49}\)
简化:\(\frac{6}{17}⋅\frac{11}{25}⋅\frac{17}{6}\)。
- 回答
-
\(\frac{11}{25}\)
下一个例子让我们意识到 0 除以某个数字或将某个数字除以 0 之间的区别。
简化:a.\(\frac{0}{n+5}\),其中\(n\neq −5\) b.\(\frac{10−3p}{0}\) 哪里\(10−3p\neq 0.\)
- 回答
-
一个。
\(\begin{array}{lc} {} & \dfrac{0}{n+5} \\ \text{Zero divided by any real number except itself is 0.} & 0 \end{array}\)
b。
\(\begin{array}{lc} {} & \dfrac{10−3p}{0} \\ \text{Division by 0 is undefined.} & \text{undefined} \end{array}\)
简化:a.\(\frac{0}{m+7}\),其中\(m\neq −7\) b.\(\frac{18−6c}{0}\),哪里\(18−6c\neq 0\)。
- 回答
-
a. 0
b. 未定义
简化:a.\(\frac{0}{d−4}\),其中\(d\neq 4\) b.\(\frac{15−4q}{0}\),哪里\(15−4q\neq 0\)。
- 回答
-
a. 0
b. 未定义
使用分布属性简化表达式
假设三个朋友要去看电影。 他们每人需要 9.25 美元(即 9 美元和 1 个季度)来支付门票。 他们总共需要多少钱?
你可以将美元与季度分开考虑。 他们需要 3 倍 9 美元,所以 27 美元,1 个季度需要 3 倍,所以 75 美分。 他们总共需要27.75美元。 如果你考虑用这种方式进行数学运算,你就是在使用分布属性。
\(\begin{array}{lc} \text{If }a,b \text{,and }c \text{are real numbers, then} \; \; \; \; \; & a(b+c)=ab+ac \\ {} & (b+c)a=ba+ca \\ {} & a(b−c)=ab−ac \\{} & (b−c)a=ba−ca \end{array}\)
简化:\(3(x+4)\)。
- 回答
-
\(\begin{array} {} & 3(x+4) \\ \text{Distribute.} \; \; \; \; \; \; \; \; & 3·x+3·4 \\ \text{Multiply.} & 3x+12 \end{array}\)
简化:\(4(x+2)\)。
- 回答
-
\(4x8\)
简化:\(6(x+7)\)。
- 回答
-
\(6x42\)
有些学生发现用箭头来提醒他们如何使用分布式财产会很有帮助。 然后,示例中的第一步将如下所示:
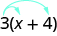
简化:\(8(\frac{3}{8}x+\frac{1}{4})\)。
- 回答
-
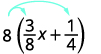
分发。 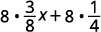
乘以。 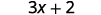
简化:\(6(\frac{5}{6}y+\frac{1}{2})\)。
- 回答
-
\(5y+3\)
简化:\(12(\frac{1}{3}n+\frac{3}{4})\)
- 回答
-
\(4n+9\)
当我们在后面的章节中解决货币申请时,使用下一个示例中所示的 Distributive Property 将非常有用。
简化:\(100(0.3+0.25q)\)。
- 回答
-
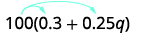
分发。 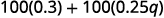
乘以。 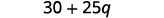
简化:\(100(0.7+0.15p).\)
- 回答
-
\(70+15p\)
简化:\(100(0.04+0.35d)\)。
- 回答
-
\(4+35d\)
当我们分配一个负数时,我们需要格外小心,使符号正确!
简化:\(−11(4−3a).\)
- 回答
-
\(\begin{array}{lc} {} & −11(4−3a) \\ \text{Distribute. } \; \; \; \; \; \; \; \; \; \;& −11·4−(−11)·3a \\ \text{Multiply.} & −44−(−33a) \\ \text{Simplify.} & −44+33a \end{array}\)
请注意,你也可以将结果写成 “\(33a−44.\)你知道为什么吗?
简化:\(−5(2−3a)\)。
- 回答
-
\(−10+15a\)
简化:\(−7(8−15y).\)
- 回答
-
\(−56+105y\)
在下一个示例中,我们将演示如何使用分布属性来查找与表达式相反的内容。
简化:\(−(y+5)\)。
- 回答
-
\(\begin{array}{lc} {} & −(y+5) \\ \text{Multiplying by }−1 \text{ results in the opposite.}& −1(y+5) \\ \text{Distribute.} & −1·y+(−1)·5 \\ \text{Simplify.} & −y+(−5) \\ \text{Simplify.} & −y−5 \end{array} \)
简化:\(−(z−11)\)。
- 回答
-
\(−z+11\)
简化:\(−(x−4)\)。
- 回答
-
\(−x+4\)
有时我们需要使用分布式财产作为操作顺序的一部分。 首先看圆括号。 如果括号内的表达式无法简化,则下一步是使用分布属性进行乘法,这将删除圆括号。 接下来的两个例子将说明这一点。
简化:\(8−2(x+3)\)
- 回答
-
我们遵循操作顺序。 乘法先于减法,所以我们先分配 2 然后减去。
\(\begin{array}{lc} {} & \text{8−2(x+3)} \\ \text{Distribute.} & 8−2·x−2·3 \\ \text{Multiply.} & 8−2x−6 \\ \text{Combine like terms.} &−2x+2 \end{array}\)
简化:\(9−3(x+2)\)。
- 回答
-
\(3−3x\)
简化:\(7x−5(x+4)\)。
- 回答
-
\(2x−20\)
简化:\(4(x−8)−(x+3)\)。
- 回答
-
\(\begin{array}{lc} {} & 4(x−8)−(x+3) \\ \text{Distribute.} & 4x−32−x−3 \\ \text{Combine like terms.} & 3x−35 \end{array}\)
简化:\(6(x−9)−(x+12)\)。
- 回答
-
\(5x−66\)
简化:\(8(x−1)−(x+5)\)。
- 回答
-
\(7x−13\)
这里总结了我们在本章中使用的所有实数属性。
| 可交换财产
相加或乘法时,更改顺序会得到相同的结果 \[\begin{array}{lll} \textbf{of Addition} & \text{If }a \text{ and }b \text{are real numbers, then} & a+b=b+a. \\ \textbf{of Multiplication} & \text{If }a \text{ and }b \text{are real numbers, then} & a·b=b·a. \end{array} \] |
| 关联财产
相加或乘法时,更改分组会得到相同的结果。 \[\begin{array}{lll} \textbf{of Addition} & \text{If }a,b, \text{ and }c \text{ are real numbers, then} & (a+b)+c=a+(b+c). \\ \textbf{of Multiplication} & \text{If }a,b,\text{ and }c \text{ are real numbers, then} & (a·b)·c=a·(b·c). \end{array} \] |
| 分销财产
\[\begin{array}{lc} \text{If }a,b \text{,and }c \text{are real numbers, then} \; \; \; \; \; & a(b+c)=ab+ac \\ {} & (b+c)a=ba+ca \\ {} & a(b−c)=ab−ac \\{} & (b−c)a=ba−ca \end{array}\] |
| 身份财产 \[\begin{array}{ll} \textbf{of Addition} \text{ For any real number }a:a+0=a & 0+a=a \\ \;\;\;\; \textbf{0} \text{ is the } \textbf{additive identity} \\ \textbf{of Multiplication} \text{ For any real number } a:a·1=a & 1·a=a \\ \;\;\;\; \textbf{1} \text{ is the } \textbf{multiplicative identity} \end{array}\] |
| 反向属性
\[\begin{array}{lc} \textbf{of addition } \text{For any real number }a, & a+(−a)=0 \\ \;\;\;\; −a \text{ is the } \textbf{additive inverse }\text{ of }a & {} \\ \;\;\;\; \text{A number and its } \textit{opposite } \text{add to zero.} \\ \\ \\ \textbf{of multiplication } \text{For any real number }a,a\neq 0 & a·\dfrac{1}{a}=1 \\ \;\;\;\;\;\dfrac{1}{a} \text{ is the } \textbf{multiplicative inverse} \text{ of }a \\ \;\;\;\; \text{A number and its } \textit{reciprocal} \text{ multiply to one.} \end{array}\] |
| 零的属性 \[\begin{array}{lc} \text{For any real number }a, & a·0=0 \\ {} & 0·a=0 \\ \text{For any real number }a,a\neq 0, & \dfrac{0}{a}=0 \\ \text{For any real number }a, & \dfrac{a}{0} \text{ is undefined} \end{array}\] |
关键概念
| Commutative Pro perty 相加或乘法 时,更改顺序会得到相同的结果 \[\begin{array}{lll} \textbf{of Addition} & \text{If }a \text{ and }b \text{are real numbers, then} & a+b=b+a. \\ \textbf{of Multiplication} & \text{If }a \text{ and }b \text{are real numbers, then} & a·b=b·a. \end{array} \] |
| 关联属性相加或乘法时,更改分组会得到相同的结果。 \[\begin{array}{lll} \textbf{of Addition} & \text{If }a,b, \text{ and }c \text{ are real numbers, then} & (a+b)+c=a+(b+c). \\ \textbf{of Multiplication} & \text{If }a,b,\text{ and }c \text{ are real numbers, then} & (a·b)·c=a·(b·c). \end{array} \] |
| 分销财产
\[\begin{array}{lc} \text{If }a,b \text{,and }c \text{are real numbers, then} \; \; \; \; \; & a(b+c)=ab+ac \\ {} & (b+c)a=ba+ca \\ {} & a(b−c)=ab−ac \\{} & (b−c)a=ba−ca \end{array}\] |
| 身份财产
\[\begin{array}{ll} \textbf{of Addition} \text{ For any real number }a:a+0=a & 0+a=a \\ \;\;\;\; \textbf{0} \text{ is the } \textbf{additive identity} \\ \textbf{of Multiplication} \text{ For any real number } a:a·1=a & 1·a=a \\ \;\;\;\; \textbf{1} \text{ is the } \textbf{multiplicative identity} \end{array}\] |
| 反向属性
\[\begin{array}{lc} \textbf{of addition} \text{For any real number }a, & a+(−a)=0 \\ \;\;\;\; −a \text{ is the } \textbf{additive inverse }\text{ of }a & {} \\ \;\;\;\; \text{A number and its } \textit{opposite } \text{add to zero.} \\ \\ \\ \textbf{of multiplication } \text{For any real number }a,a\neq 0 & a·\dfrac{1}{a}=1 \\ \;\;\;\;\;\dfrac{1}{a} \text{ is the } \textbf{multiplicative inverse} \text{ of }a \\ \;\;\;\; \text{A number and its } \textit{reciprocal} \text{ multiply to one.} \end{array}\] |
| 零的属性
\[\begin{array}{lc} \text{For any real number }a, & a·0=0 \\ {} & 0·a=0 \\ \text{For any real number }a,a\neq 0, & \dfrac{0}{a}=0 \\ \text{For any real number }a, & \dfrac{a}{0} \text{ is undefined} \end{array}\] |
词汇表
- 加法身份
- 数字 0 是加法标识,因为将 0 与任何数字相加都不会改变其值。
- 加法反向
- 与数字相反的是其相加的逆数。
- 乘法身份
- 数字 1 是乘法恒等式,因为将 1 乘以任何数字都不会改变其值。
- 乘法逆函数
- 数字的倒数是其乘法逆数。


