1.5: 小数
- Page ID
- 203966
在本节结束时,您将能够:
- 四舍五入小数
- 加上和减去小数
- 乘以和除以小数
- 转换小数、分数和百分比
- 使用平方根简化表达式
- 识别整数、有理数、非理数和实数
- 在数字行上找到分数和小数
可以在基本代数章节 “基础” 中找到对本节所涵盖主题的更详尽的介绍。
四舍五进制小数
小数是另一种写分数的方式,分母是十的幂数。
\[\begin{array}{rcll} 0.1 & = & \dfrac{1}{10} & \text{is “one tenth”} \\ 0.01 & = & \dfrac{1}{100} & \text{is “one hundredth”} \\ 0.001 & = & \dfrac{1}{1000} & \text{is “one thousandth”} \\ 0.0001 & = & \dfrac{1}{10,000} & \text{is “one ten-thousandth”} \end{array}\]
就像整数一样,十进制的每位数字对应于基于十的幂的位值。 该@@ 图显示了小数点左侧和右侧的位置值的名称。
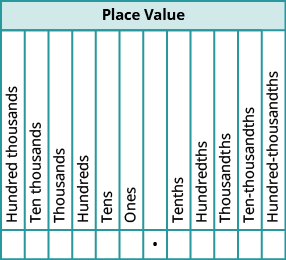
当我们处理小数时,通常需要将数字四舍五入到最接近的所需位值。 我们在此总结四舍五入小数的步骤。
- 找到给定的位值并用箭头标记。
- 为位值右边的数字加下划线。
- 带下划线的数字是否大于或等于 5?
- 是:在给定位数值的数字上加 1。
- 否:请勿更改给定位数值中的数字
- 重写数字,删除四舍五入数字右侧的所有数字。
四舍五入\(18.379\)到最接近的 ⓐ 第一百 ⓑ 十 ⓒ 整数。
- 回答
-
回合\(18.379.\)
ⓐ 到最接近的百分之一
用箭头找到第100个位置。 
为给定位数右边的数字加下划线。 
因为 9 大于或等于 5,所以将 1 与 7 相加。 
重写数字,删除四舍五入数字右侧的所有数字。 
请注意,删除的数字并未替换为零。 
ⓑ 到最接近的十分之一
用箭头找到第十个位置。 
为给定位数右边的数字加下划线。 
由于 7 大于或等于 5,因此将 1 与 3 相加。 
重写数字,删除四舍五入数字右侧的所有数字。 
请注意,删除的数字并未替换为零。 
ⓒ 到最接近的整数
用箭头找到那个地方。 
为给定位数右边的数字加下划线。 
由于 3 不大于或等于 5,因此请勿将 1 与 8 相加。 
重写数字,删除四舍五入数字右侧的所有数字。 

四舍五入\(6.582\)到最接近的 ⓐ 第一百 ⓑ 十 ⓒ 整数。
- 回答
-
ⓐ\(6.58\) ⓑ\(6.6\) ⓒ\(7\)
四舍五入\(15.2175\)到最接近的 ⓐ 千分之一 ⓑ 第一百 ⓒ 十分之一。
- 回答
-
ⓐ\(15.218\) ⓑ\(15.22\)
ⓒ\(15.2\)
加上和减去小数
要加上或减去小数,我们将小数点对齐。 通过以这种方式排列小数点,我们可以加上或减去相应的位值。 然后,我们将数字相加或减去,就好像它们是整数一样,然后将小数点放在总和中。
- 确定总和或差值的符号。
- 写下数字,使小数点垂直排列。
- 根据需要使用零作为占位符。
- 将数字相加或减去,就好像它们是整数一样。 然后将答案中的
小数点放在给定数字的小数点下方。 - 用相应的符号写下总和或差值。
加上或减去:ⓐ\(−23.5−41.38\) ⓑ\(14.65−20.\)
- 回答
-
ⓐ
\(\begin{array}{ll} \text{} & −23.5−41.38 \\ \\ \\ {\text{The difference will be negative. To subtract, we add the} \\ \text{numerals. Write the numbers so the decimal points line} \\ \text{up vertically.}} & { \; \; 23.5 \\ \underline{+41.38}} \\ \\ \\ { \text{Put 0 as a placeholder after the 5 in 23.5.} \\ \text{Remember, } \frac{5}{10}=\frac{50}{100} \text{ so } 0.5=0.50.} & { \; \; 23.50 \\ \underline{+41.38}} \\ \\ \\ {\text{Add the numbers as if they were whole numbers.} \\ \text{Then place the decimal point in the sum.}} & {\; \; 23.50 \\ \underline{+41.38} \\ \; \; 64.88 } \\ \\ \\ \text{ Write the result with the correct sign.} & 64.88−23.5−41.38=−64.88 \end{array}\)
ⓑ
\(\begin{array}{ll} \text{} & 14.65−20 \\ \\ \\ {\text{The difference will be negative. To subtract, we} \\ \text{subtract 14.65 from 20.}} \\ \\ \\ {\text{Write the numbers so the decimal points line up} \\ \text{vertically.}} & { \; \; 20 \\ \underline{−14.65}} \\ \\ \\ {\text{Remember, 20 is a whole number, so place the} \\ \text{decimal point after the 0.}} \\ \\ \\ \text{Put in zeros to the right as placeholders.} & { \; \; 20.00 \\ \underline{−14.65}} \\ \\ \\ \text{Subtract and place the decimal point in the answer.} & {\begin{array}{lcccc} {} & 9 & {} & 9 & {} \\ 1 & \cancel{10} & {} & \cancel{10} & 10 \\ 2 & 0 & . & 0 & 0 \\ −1 & 4 & . & 6 & 5 \end{array} \\ \text{______________________} \\ \begin{array}{lcccc} {\; \; \; \; \; \; \; \; \; } & 5 & . & 3 & 5 \end{array}} \\ \\ \\ \text{Write the result with the correct sign.} & 14.65−20=−5.35 \end{array} \)
加上或减去:ⓐ\(−4.8−11.69\) ⓑ\(9.58−10\)。
- 回答
-
ⓐ\(−16.49\) ⓑ\(−0.42\)
加上或减去:ⓐ\(−5.123−18.47\) ⓑ\(37.42−50\)。
- 回答
-
ⓐ\(−23.593\) ⓑ\(−12.58\)
乘以和除以小数
当我们乘以有符号小数时,首先我们确定乘积的符号,然后相乘,就好像数字都是正数一样。 我们暂时将数字相乘,忽略小数点,然后计算因子中的小数点数,该总和告诉我们乘积中的小数位数。 最后,我们在产品上写上相应的标志。
- 确定产品的标志。
- 以垂直格式书写,将右边的数字排成一列。 将数字相乘,就好像它们是整数一样,暂时忽略小数点。
- 放置小数点。 乘积中的小数位数是因子中小数位数的总和。
- 在产品上写上相应的标志。
乘以:\((−3.9)(4.075)\)。
- 回答
-
\((−3.9)(4.075)\) 迹象不同。 该产品
将是负面的。该产品将是负面的。 以垂直格式书写,将右边的
数字对齐。
乘。 
将因子中的
小数位数相加 (1 + 3)。 将小数点置于右边 4 位。

迹象不同,所以产品是负面的。 \((−3.9)(4.075)=−15.8925\)
乘以:\(−4.5(6.107)\)。
- 回答
-
\(−27.4815\)
乘以:\(−10.79(8.12)\)。
- 回答
-
\(−87.6148\)
通常,尤其是在科学领域,你会将小数乘以 10 的乘方(10、100、1000 等)。 如果你将纸上的几个产品相乘,你可能会注意到一种模式,它将 10 的次方零数与小数位数联系起来,我们将小数点向右移动以得到该乘积。
将@@
- 将小数点向右移动,其位
数与 10 的幂次数相同。 - 根据需要在数字末尾添加零。
乘以:5.63 乘以 ⓐ 10 ⓑ 100 ⓒ 1000。
- 回答
-
通过查看十倍数中的零数,我们可以看到向右移动十进制所需的位数。
ⓐ
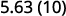
10 中有 1 个零,因此将小数点向右移动 1 位。 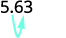
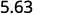
ⓑ
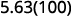
100 中有 2 个零,因此将小数点向右移动 2 位。 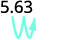

ⓒ
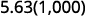
1,000 中有 3 个零,因此将小数点向右移动 3 位。 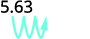
必须将零加到末尾。 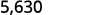
将 2.58 乘以 ⓐ 10 ⓑ 100 ⓒ 1000。
- 回答
-
ⓐ 25.8 ⓑ 258 ⓒ 2,580
将 14.2 乘以 ⓐ 10 ⓑ 100 ⓒ 1000。
- 回答
-
ⓐ 142 ⓑ 1,420 ⓒ 14,200
就像乘法一样,有符号小数的除法与整数相除非常相似。 我们只需要弄清楚小数点必须放在哪里以及商的符号即可。 除以有符号小数时,首先确定商的符号,然后像数字都是正数一样进行除法。 最后,用适当的符号写下商。
我们回顾一下除法的符号和词汇:

为了便于参考,我们将写出除以小数时要采取的步骤。
- 确定商的符号。
- 将小数点一直向右 “移动”,使除数成为整数。 将除数中的小数点 “移动” 到相同数量的位数——根据需要添加零。
- 除以。 将小数点置于除息小数点上方的商数中。
- 用适当的符号写出商。
除以:\(−25.65÷(−0.06)\)。
- 回答
-
请记住,由于等效分数属性,你可以 “移动” 除数和除数中的小数。
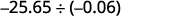
迹象是一样的。 商是正数。 将小数点一直向右 “移动”,使除数成为整数。 将除数中的小数点 “移动” 相同的位数。 
除以。 将小数点置于除息小数点上方的商数中。 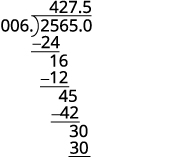
用适当的符号写出商。 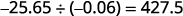
除以:\(−23.492÷(−0.04)\)。
- 回答
-
\(587.3\)
除以:\(−4.11÷(−0.12)\)。
- 回答
-
\(34.25\)
转换小数、分数和百分比
在我们的工作中,通常需要更改数字的形式。 我们可能需要将分数更改为小数或将小数更改为百分比。
我们通过识别最后一个(最右边)数字的位值将小数转换为分数。 在十进制 0.03 中,3 位于百分之一位,所以 100 是等于 0.03 的分数的分母。
\[0.03=\dfrac{3}{100}\]
过程框中总结了将小数转换为分数所要采取的步骤。
- 要将小数转换为正确的分数,请确定最后一个数字的位值。
- 写下分数。
- 分子-小数点右边的 “数字”
- 分母-与最后一位数字对应的位值
- 要将分数转换为十进制,请将分数的分子除以分数的分母。
写:ⓐ\(0.374\) 作为分数 ⓑ\(−\frac{5}{8}\) 作为十进制。
- 回答
-
ⓐ
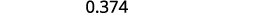
确定最后一位数字的位值。 
写下 0.374 的分数:分子是 374。 分母为 1,000。 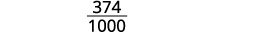
简化分数。 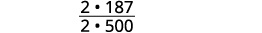
除去常见因素。 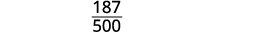
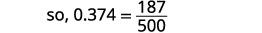
ⓑ 由于分数条表示除法,因此我们首先将分数写\(\frac{5}{8}\)为\(8\sqrt{5}\)。 现在分开。
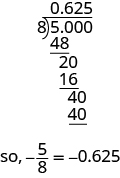
写:ⓐ\(0.234\) 作为分数 ⓑ\(−\frac{7}{8}\) 作为十进制。
- 回答
-
ⓐ\(\frac{117}{500}\) ⓑ\(−0.875\)
写:ⓐ\(0.024\) 作为分数 ⓑ\(−\frac{3}{8}\) 作为十进制。
- 回答
-
ⓐ\(\frac{3}{125}\) ⓑ\(−0.375\)
百分比是分母为 100 的比率。 百分比表示每百。 我们使用百分比符号% 来显示百分比。 由于百分比是一个比率,因此可以很容易地将其表示为分数。 百分比表示每 100,因此分数的分母为 100。 然后,我们将分子除以分母,将分数更改为十进制。 做了很多次之后,你可能会看到图案。
要将百分数转换为十进制数,我们将小数点向左移动两位。
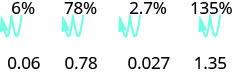
要将小数转换为百分比,请记住百分比表示每百。 如果我们将十进制更改为分母为 100 的分数,则很容易将该分数更改为百分比。 经过多次转换,你可能会认出这种模式。
要将小数转换为百分比,我们将小数点向右移动两位,然后添加百分号。
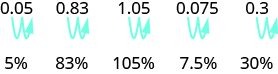
将@@
- 要将百分比转换为小数,请在删除百分号后将小数点向左移动两位。
- 要将小数转换为百分比,请将小数点向右移动两位,然后添加百分号。
分别转换:
ⓐ 百分比到十进制:62%、135% 和 13.7%。
ⓑ 十进制到百分比:0.51、1.25 和 0.093。
- 回答
-
ⓐ
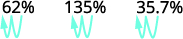
将小数点向左移动两位。 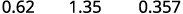
ⓑ
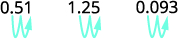
将小数点向右移动两位。 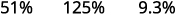
分别转换:
ⓐ 百分比到十进制:9%、87% 和 3.9%。
ⓑ 十进制到百分比:0.17、1.75 和 0.0825。
- 回答
-
ⓐ 0.09、0.87、0.039 ⓑ 17%、175%、8.25%
分别转换:
ⓐ 百分比到十进制:3%、91% 和 8.3%。
ⓑ 十进制到百分比:0.41、2.25 和 0.0925。
- 回答
-
ⓐ 0.03、0.91、0.083 ⓑ 41%、225%、9.25%
使用平方根简化表达式
请记住,当一个数字\(n\)乘以自身时,我们将其写入\(n^2\)和读取 “\(n\)平方”。 结果称为数字 n 的平方。 例如,读\(\frac{8}{2}\)为 “8 平方”,64 被称为 8 的平方。 同样,121 是 11 的平方,因为\(11^2\)是 121。 学会识别完美的平方数会很有帮助。
if\(n^2=m\),那么 m 是 n 的平方。
那负数的平方呢? 我们知道,当两个数字的符号相同时,它们的乘积是正数。 因此,任何负数的平方也是正数。
\[(−3)^2=9 \; \; \; \; \; \; \; \; \; (−8)^2=64 \; \; \; \; \; \; \; \; \; (−11)^2=121 \; \; \; \; \; \; \; \; \; (−15)^2=225\]
因为\(10^2=100\),我们说 100 是 10 的平方。 我们还说 10 是 100 的平方根。 平方为 m 的数字称为数字 m 的平方根。
if\(n^2=m\),则 n 是 m 的平方根。
\((−10)^2=100\)另请注意,所以 −10 也是 100 的平方根。 因此,10 和 −10 都是 100 的平方根。 因此,每个正数都有两个平方根——一个正数和一个负数。 激进符号\(\sqrt{m}\),表示正平方根。 正平方根称为主平方根。 当我们使用激进符号时,这总是意味着我们想要主平方根。
\(\sqrt{m}\)读作 “mm 的平方根”。
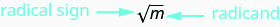
如果\(m=n^2\),那么\(\sqrt{m}=n\),对于\(n≥0\)。
m 的平方根是正数\(\sqrt{m}\),其平方为 m。
我们知道每个正数都有两个平方根,激进符号表示正数。 我们写\(\sqrt{100}=10\)。 如果我们想找到一个数字的负平方根,我们在激进符号前面放一个负数。 例如,\(−\sqrt{100}=−10\)。 我们读\(−\sqrt{100}\)作 “与 10 的主平方根相反”。
简化:ⓐ\(\sqrt{25}\) ⓑ\(\sqrt{121}\) ⓒ\(−\sqrt{144}\)。
- 回答
-
ⓐ
\(\begin{array}{ll} \text{} & \sqrt{25} \\ \text{Since }5^2=25 & 5 \end{array}\)ⓑ
\(\begin{array}{ll} \text{} & \sqrt{121} \\ \text{Since }11^2=121 & 11 \end{array}\)
ⓒ
\(\begin{array}{ll} {} & −\sqrt{144} \\ \text{The negative is in front of} & −12 \\ \text{the radical sign.} \end{array}\)
简化:ⓐ\(\sqrt{36}\) ⓑ\(\sqrt{169}\) ⓒ\(−\sqrt{225}\)
- 回答
-
ⓐ 6 ⓑ 13 ⓒ −15
简化:ⓐ\(\sqrt{16}\) ⓑ\(\sqrt{196}\) ⓒ\(−\sqrt{100}\)
- 回答
-
ⓐ 4 ⓑ 14 ⓒ −10
识别整数、有理数、非理数和实数
我们已经将数字描述为计数数字 s、整数 s 和整数。 这些类型的数字有什么区别? 差异可能与减法混淆。 问问我们如何区分这些类型的数字怎么样?
\[\begin{array}{ll} \text{Counting numbers} & 1,2,3,4,….. \\ \text{Whole numbers} & 0,1,2,3,4,…. \\ \text{Integers} & ….−3,−2,−1,0,1,2,3,…. \end{array}\]
如果我们从所有整数开始,然后包括所有分数,我们会得到什么类型的数字? 我们会得到的数字构成了有理数的集合。 有理数是一个可以写成两个整数之比的数字。
通常,任何在数位后结尾的十进制(例如 7.3 或 −1.2684)都是有理数。 当将十进制写成分数时,我们可以使用最后一位数字的位值作为分母。 的十进制\(\frac{1}{3}\)是数字\(0.\overline{3}\)。 3 上方的条形表示数字 3 无限重复。 持续在微积分中具有重要意义。 条形图下方的数字称为重复方块,它会连续重复。
由于所有整数都可以写成分母为 1 的分数,因此整数(以及计数和整数)都是有理数。
每个有理数既可以写成整数的比率\(\frac{p}{q}\),其中 p 和 q 是整数和\(q≠0\),也可以写成停止或重复的十进制。
有理数是一种形式的数字\(\frac{p}{q}\),其中 p 和 q 是整数和\(q≠0\)。
它的十进制形式停止或重复。
有没有不停止或重复的小数? 是的! 数字(希腊字母 pi,发音为 “pie”)在描述圆圈时非常重要,其十进制形式不会停止或重复。 我们使用三个点 (...) 来表示十进制不停止或重复。
\[π=3.141592654...\]
不是完美平方的数字的平方根是不会停止或重复的十进制。
十进制形式不停止或重复的数字不能写成整数的分数。 我们称之为非理性数字。
非理数是不能写成两个整数之比的数字。
它的十进制形式不会停止,也不会重复。
让我们总结一种方法,我们可以用来确定一个数字是有理的还是非理性的。
如果是数字的十进制形式
- 重复或停止,该数字是一个有理数。
- 不重复也不停止,这个数字是一个非理性的数字。
我们已经看到,所有计数数都是整数,所有整数都是整数,所有整数都是有理数。 非理性数是十进制形式不停止且不重复的数字。 当我们将有理数和非理数放在一起时,我们得到了一组实数 s。
实数是有理或非理性的数字。
在本课程的后面部分,我们将介绍实数之外的数字。 该图说明了我们到目前为止使用的数字集是如何组合在一起的。
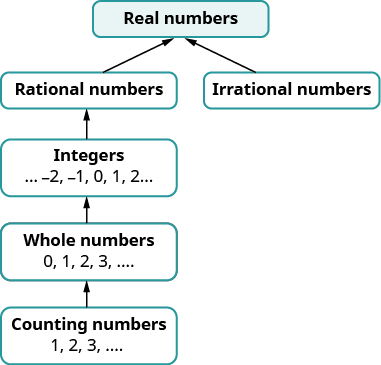
“实数” 一词对你来说似乎很奇怪吗? 有没有不是 “真实” 的数字,如果有,它们可能是什么? 我们可以简化\(−\sqrt{25}\)吗? 有数字的正方形\(−25\)吗?
\[()^2=−25?\]
到目前为止,我们处理的数字中没有一个是正方形\(−25\)。 为什么? 任何正数的平方均为正数。 任何负数平方均为正数。 所以我们说没有实数等于\(\sqrt{−25}\)。 负数的平方根不是实数。
给定数字\(−7,\frac{14}{5},8,\sqrt{5},5.9,−\sqrt{64}\),列出 ⓐ 整数 ⓑ 整数 ⓒ 有理数 ⓓ 非理性数字 ⓔ 实数。
- 回答
-
ⓐ 记住,整数\(0,1,2,3,…,\)是 8 是唯一给出的整数。
ⓑ 整数是整数及其对立面(包括 0)。 所以整数 8 是一个整数,而 −7 与整数相反,所以它也是一个整数。 另外,请注意,64 是 8 的平方,所以\(−\sqrt{64}=−8\)。 所以整数是\(−7,8,\)和\(−\sqrt{64}\)。
ⓒ 由于所有整数都是有理的,那么\(−7,8,\)和\(−\sqrt{64}\)都是有理的。 有理数还包括重复或停止的分数和小数,因此\(\frac{14}{5}\)\(5.9\)是有理的。 因此,有理数列表是\(−7,\frac{14}{5},8,5.9,\)和\(−\sqrt{64}\)。
ⓓ 请记住,5 不是一个完美的正方形,所以\(\sqrt{5}\)是不合理的。
ⓔ 列出的所有数字均为实数。
给定数字\(−3,−\sqrt{2},0.\overline{3},\frac{9}{5},4,\sqrt{49},\)列出 ⓐ 整数 ⓑ 整数 ⓒ 有理数
ⓓ 非理性数字 ⓔ 实数。
- 回答
-
ⓐ\(4,\sqrt{49}\) ⓑ\(−3,4,\sqrt{49}\)
ⓒ\(−3,0.\overline{3},\frac{9}{5},4,\sqrt{49}\) ⓓ\(−\sqrt{2}\)ⓔ\(−3,−\sqrt{2},0.\overline{3},\frac{9}{5},4,\sqrt{49}\)
给定数字\(−\sqrt{25},−\frac{3}{8},−1,6,\sqrt{121},2.041975...,\)列出 ⓐ 整数 ⓑ 整数 ⓒ 有理数 ⓓ 非理性数字 ⓔ 实数。
- 回答
-
ⓐ\(6,\sqrt{121}\)
ⓑ\(−\sqrt{25},−1,6,\sqrt{121}\)
ⓒ\(−\sqrt{25},−\frac{3}{8},−1,6,\sqrt{121}\)
ⓓ\(2.041975...\)
ⓔ\(−\sqrt{25},−\frac{3}{8},−1,6,\sqrt{121},2.041975...\)
在数字行上找到分数和小数
我们现在要在数字行上包含分数和小数。 让我们从分数开始,在数字行\(\frac{8}{3}\)上找到\(\frac{1}{5},−\frac{4}{5},3,\frac{7}{4},−\frac{9}{2},−5\)和。
我们将从整数 3 和 −5 开始,因为它们最容易绘制。 参见图。
列出的正确分数是\(\frac{1}{5}\),\(−\frac{4}{5}.\)我们知道正确的分\(\frac{1}{5}\)数的值小于一,因此将位于 0 和 1 之间。 分母为 5,因此我们将从 0 到 1 的单位分成 5 个相等的部分\(\frac{1}{5},\frac{2}{5},\frac{3}{5},\frac{4}{5}\)。 我们策划\(\frac{1}{5}\)。
同样,介\(−\frac{4}{5}\)于 0 和 −1 之间。 将单位分成 5 个相等的部分后,我们绘制图样\(−\frac{4}{5}\)。
最后,看看不正确的分数\(\frac{7}{4},\frac{9}{2},\frac{8}{3}\)。 如果将每个点更改为混合数字,则定位这些点可能会更容易。
\[\dfrac{7}{4}=1\dfrac{3}{4} \; \; \; \; \; \; \; \; \; −\dfrac{9}{2}=−4\dfrac{1}{2} \; \; \; \; \; \; \; \; \; \dfrac{8}{3}=2\dfrac{2}{3}\]
该图显示了绘制了所有点的数字线。

在数字行上找到并标记以下内容:\(4,\frac{3}{4},−\frac{1}{4},−3,\frac{6}{5},−\frac{5}{2},\)和\(\frac{7}{3}\)。
- 回答
-
找到并绘制整数,\(4,−3.\)
\(\frac{3}{4}\)首先找到正确的分数。 分数介\(\frac{3}{4}\)于 0 和 1 之间。 将 0 和 1 之间的距离分成四个相等的部分,然后我们绘制图\(\frac{3}{4}\)。 同样的情节\(−\frac{1}{4}\)。
现在找到不正确的分数\(\frac{6}{5},−\frac{5}{2},\),然后\(\frac{7}{3}\). 如果我们将它们转换为混合数字,然后如上所述绘制它们,则绘制它们会更容易:\(\frac{6}{5}=1\frac{1}{5},−\frac{5}{2}=−2\frac{1}{2},\frac{7}{3}=2\frac{1}{3}\).

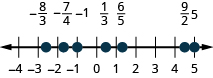
在数字行上找到并标记以下内容:\(−1,\frac{1}{3},\frac{6}{5},−\frac{7}{4},\frac{9}{2},5,−\frac{8}{3}\).
- 回答
-
在数字行上找到并标记以下内容:\(−2,\frac{2}{3},\frac{7}{5},−\frac{7}{4},\frac{7}{2},3,−\frac{7}{3}\).
- 回答
-
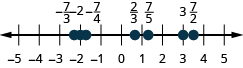
由于小数是分数的形式,因此在数字行上定位小数与在数字行上定位分数类似。
在数字行上找到:ⓐ 0.4 ⓑ −0.74。
- 回答
-
ⓐ 十进制数 0.4 等同于\(\frac{4}{10}\)一个恰当的分数,所以 0.4 位于 0 和 1 之间。 在数字线上,将 0 和 1 之间的间隔分成 10 个相等的部分。 现在给零件加上标签 0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9、1.0。 我们将0写为0.0,将1写为1.0,这样数字就一致地以十分之一为单位。 最后,在数字行上标记 0.4。

ⓑ 十进制等同\(−0.74\)于\(−\frac{74}{100}\),因此它位于 0 和 .−1 之间。 在数字行上,标记并标出 0 到 −1 间隔内的百分比。

在数字行上找到:ⓐ\(0.6\) ⓑ\(−0.25.\)
- 回答
-
ⓐ

ⓑ
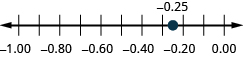
在数字行上找到:ⓐ 0.90.9 ⓑ −0.75.−0.75。
- 回答
-
ⓐ

ⓑ
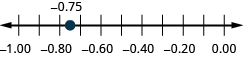
访问此在线资源以获取更多指导和使用小数进行练习。
- 算术基础知识:除以小数
关键概念
- 如何四舍五入小数。
- 找到给定的位值并用箭头标记。
- 为位值右边的数字加下划线。
- 带下划线的数字是否大于或等于 5?
- 是:在给定位数值的数字上加 1。
- 否:请勿更改给定位数值中的数字
- 重写数字,删除四舍五入数字右侧的所有数字。
- 如何添加或减去小数。
- 确定总和或差值的符号。
- 写下数字,使小数点垂直排列。
- 根据需要使用零作为占位符。
- 将数字相加或减去,就好像它们是整数一样。 然后将答案中的小数点放在给定数字的小数点下方。
- 用相应的符号写下总和或差值
- 如何乘以小数。
- 确定产品的标志。
- 以垂直格式书写,将右边的数字排成一列。 将数字相乘,就好像它们是整数一样,暂时忽略小数点。
- 放置小数点。 乘积中的小数位数是因子中小数位数的总和。
- 在产品上写上相应的标志。
- 如何将十进制乘以十的乘方。
- 将小数点向右移动,其位数与 10 的幂次数相同。
- 根据需要在数字末尾添加零。
- 如何除以小数。
- 确定商的符号。
- 将小数点一直向右 “移动”,使除数成为整数。 将除数中的小数点 “移动” 到相同数量的位数——根据需要添加零。
- 除以。 将小数点置于除息小数点上方的商数中。
- 用适当的符号写出商。
- 如何将小数转换为正确的分数并将分数转换为十进制。
- 要将小数转换为正确的分数,请确定最后一个数字的位值。
- 写下分数。
- 分子-小数点右边的 “数字”
- 分母-与最后一位数字对应的位值
- 要将分数转换为十进制,请将分数的分子除以分数的分母。
- 如何将百分比转换为十进制并将小数转换为百分比。
- 要将百分比转换为小数,请在删除百分号后将小数点向左移动两位。
- 要将小数转换为百分比,请将小数点向右移动两位,然后添加百分号。
- 平方根表示法\(\sqrt{m}\)读作 “m 的平方根”。 如果\(m=n^2\),那么\(\sqrt{m}=n\),对于\(n≥0\)。 m 的平方根是正数\(\sqrt{m}\),其平方为 m。
- 有理还是非理性如果是数字的十进制形式
- 重复或停止,该数字是一个有理数。
- 不重复也不停止,这个数字是一个非理性的数字。
- 实数
.jpg)
图 4。
词汇表
- 非理性数
- 非理数是不能写成两个整数之比的数字。 它的十进制形式不会停止,也不会重复。
- 百分之
- 百分比是分母为 100 的比率。
- 主平方根
- 正平方根称为主平方根。
- 有理数
- 有理数是一种形式的数字\(\frac{p}{q}\),其中 p 和 q 是整数和\(q≠0\)。 它的十进制形式停止或重复。
- 实数
- 实数是有理或非理性的数字。
- 数字的平方
- if\(n^2=m\),那么 m 是 n 的平方。
- 一个数字的平方根
- if\(n^2=m\),则 n 是 m 的平方根。


